汽車制動(dòng)作用下混凝土梁橋下部結(jié)構(gòu)動(dòng)力響應(yīng)分析

楊婷婷，李巖，李全林

汽車制動(dòng)作用下混凝土梁橋下部結(jié)構(gòu)動(dòng)力響應(yīng)分析

楊婷婷1，李巖2，李全林3

(1. 哈爾濱工業(yè)大學(xué) 土木工程學(xué)院，黑龍江 哈爾濱 150090；2. 哈爾濱工業(yè)大學(xué) 交通科學(xué)與工程學(xué)院，黑龍江 哈爾濱 150090；3. 深圳高速工程顧問有限公司，廣東 深圳 518094)

將制動(dòng)力系數(shù)變化擬合為時(shí)變斜坡函數(shù)，由變形協(xié)調(diào)條件和力的平衡方程推導(dǎo)車輛各輪時(shí)變制動(dòng)力，進(jìn)而建立考慮汽車制動(dòng)作用的車橋耦合空間動(dòng)力分析模型并編制計(jì)算程序。依托某混凝土梁橋工程實(shí)例，采用所編制的程序，分析汽車制動(dòng)作用下橋梁下部結(jié)構(gòu)的動(dòng)力行為特性。系統(tǒng)開展初始車速、制動(dòng)加速度上升時(shí)間、制動(dòng)峰值系數(shù)和車重等關(guān)鍵參數(shù)對橋梁下部結(jié)構(gòu)動(dòng)力響應(yīng)的影響分析。研究結(jié)果表明：車輛制動(dòng)作用下墩頂縱橋向動(dòng)力響應(yīng)顯著，且該響應(yīng)隨制動(dòng)加速度上升時(shí)間的縮短、制動(dòng)峰值系數(shù)及車重的提高而大幅增加，初始車速對其有影響但無單調(diào)性規(guī)律。

混凝土梁橋；車橋耦合振動(dòng)；制動(dòng)作用；下部結(jié)構(gòu)；動(dòng)力分析

現(xiàn)有的車橋耦合振動(dòng)研究，主要考慮車輛勻速過橋狀況，對于實(shí)際運(yùn)營中常見的車輛制動(dòng)和變速行駛等狀況較少涉及。且多數(shù)研究關(guān)注車輛制動(dòng)作用對橋梁上部結(jié)構(gòu)豎向動(dòng)力行為的影響，研究結(jié)果表明車輛制動(dòng)時(shí)引起的橋梁豎向動(dòng)力沖擊效應(yīng)較勻速作用下更為顯著[1?3]。而對于車輛制動(dòng)作用更為敏感的橋梁下部結(jié)構(gòu)，其車輛制動(dòng)作用下的動(dòng)力行為研究還鮮有報(bào)道。近年來，基于動(dòng)力的橋梁下部結(jié)構(gòu)損傷診斷相關(guān)研究已獲得廣泛關(guān)注，其中基于車橋耦合振動(dòng)的結(jié)構(gòu)損傷識別研究也得到初步開展[4]。如Foti等[5]采用數(shù)值分析和試驗(yàn)方法研究基礎(chǔ)沖刷對車輛作用下橋梁動(dòng)力響應(yīng)的影響，指出通過對車載作用下橋墩動(dòng)力響應(yīng)的比較分析進(jìn)行基礎(chǔ)沖刷識別的可行性；Prendergast等[6]通過建立車?橋?土相互作用模型分析沖刷對橋梁頻率及振型的影響，研究發(fā)現(xiàn)橋墩局部振動(dòng)對應(yīng)模態(tài)對其附近的沖刷很敏感；NIE等[7]提出基于列車動(dòng)力作用進(jìn)行橋梁下部結(jié)構(gòu)損傷診斷的理論框架，分析了列車速度、墩高及地基土種類等對橋梁動(dòng)力響應(yīng)的影響。顯然，橋梁下部結(jié)構(gòu)的水平向動(dòng)力響應(yīng)對車輛制動(dòng)作用更為敏感，因此，將車輛制動(dòng)激勵(lì)作為橋梁下部結(jié)構(gòu)損傷識別的激勵(lì)源具有很好的應(yīng)用潛力。考慮多種影響因素深入分析汽車制動(dòng)作用下橋梁下部結(jié)構(gòu)的動(dòng)力反應(yīng)特點(diǎn)和規(guī)律，可為后繼的相關(guān)研究提供基礎(chǔ)和參考。為此，本文依托實(shí)際橋例，建立考慮車輛制動(dòng)作用的車橋耦合振動(dòng)空間分析模型，系統(tǒng)分析初始車速、制動(dòng)加速度上升時(shí)間、制動(dòng)峰值系數(shù)和車重等多種關(guān)鍵因素對汽車制動(dòng)作用下橋梁下部結(jié)構(gòu)動(dòng)力響應(yīng)的影響規(guī)律，結(jié)果可為基于車輛制動(dòng)作用的橋梁下部結(jié)構(gòu)狀態(tài)評估和診斷方法研究提供依據(jù)和參考。

1 車輛和橋梁分析模型

1.1 車輛分析模型

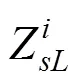
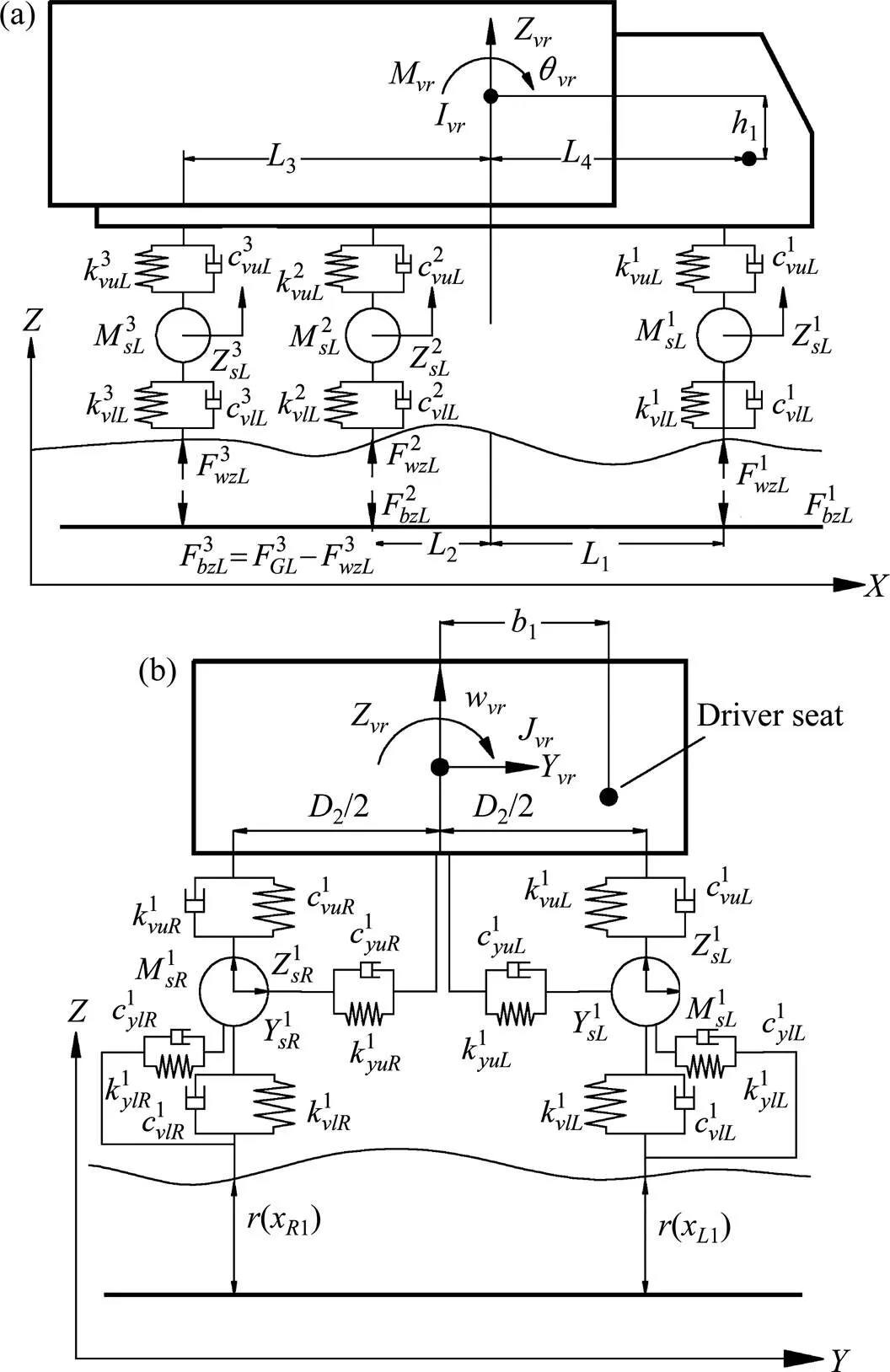
(a) 立面圖；(b) 橫斷面圖

1.2 橋梁概況與分析模型

以黑龍江寧安一座跨牡丹江的預(yù)應(yīng)力混凝土梁橋?yàn)楣こ瘫尘埃摌驑蚩绮贾脼?6?m+4×40?m+4×40?m+2×16?m，選取中跨第2聯(lián)4×40?m預(yù)應(yīng)力混凝土連續(xù)梁橋?yàn)榉治鰧ο螅瑯驅(qū)?5?m，雙向4車道布置，其橫斷面如圖2所示。主梁、橋墩、樁基分別采用C50，C30及C25混凝土；基礎(chǔ)采用鉆孔灌注樁，樁徑為2.2?m，長17~19?m；橋墩為柱式墩，直徑1.6?m，高5.5~8.4?m。支座采用板式橡膠支座(3號墩頂處)和聚四氟乙烯滑板橡膠支座(1號，2號，4號和5號墩頂處)2種形式。

單位：cm

采用Midas/Civil建立橋梁空間有限元模型(如圖3所示)，其中主梁、墩柱和樁采用空間梁單元模擬；對聚四氟乙烯滑板橡膠支座建模時(shí)一般采用雙線性模型進(jìn)行模擬[9]，但由于一輛三軸車制動(dòng)所產(chǎn)生水平荷載并未超過本橋所用型號支座的臨界摩擦力，故可對其滯回特性不予考慮，因此采用三維線性彈簧模擬支座，其6個(gè)自由度方向彈性剛度如表1所示。同時(shí)，為計(jì)入相鄰橋跨對研究對象的影響，模型中利用節(jié)點(diǎn)彈性支撐來增加邊墩順橋和橫橋向平動(dòng)約束；樁身縱向、橫向考慮周土體對樁的彈性效應(yīng)利用沿深度變化的節(jié)點(diǎn)彈性支撐模擬，雙向土彈簧約束剛度根據(jù)“m法”計(jì)算得到。

表1 支座剛度計(jì)算結(jié)果

圖3 橋梁有限元模型

2 車輛制動(dòng)作用下車橋振動(dòng)分析方法

2.1 車橋耦合振動(dòng)分析原理

對于車輛勻速過橋情況，利用車橋接觸點(diǎn)的位移和作用力的協(xié)調(diào)和平衡關(guān)系，可建立車橋耦合系統(tǒng)的整體運(yùn)動(dòng)方程：

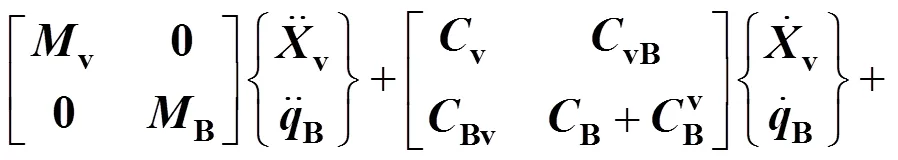
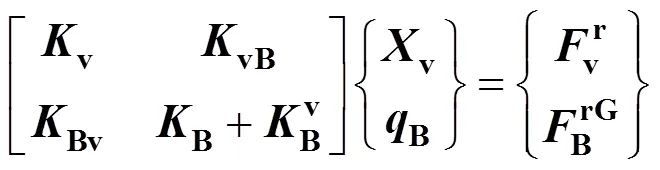
式中：，和分別為質(zhì)量、阻尼和剛度矩陣；v和B分別為車輛和橋梁位移響應(yīng)向量；表示車橋系統(tǒng)的荷載向量；符號下標(biāo)“B”代表橋梁；符號下標(biāo)“v”代表車輛；符號下標(biāo)“Bv”和“vB”表示車橋耦合項(xiàng)；符號上標(biāo)“r”和“G”分別表示由于橋面不平度和車輛自重產(chǎn)生的作用力。車橋系統(tǒng)振動(dòng)方程中的質(zhì)量、剛度、阻尼和荷載向量可由車橋系統(tǒng)間的力和位移協(xié)調(diào)條件推導(dǎo)得到，文獻(xiàn)[8]中對此具體內(nèi)容進(jìn)行了詳細(xì)推導(dǎo)，此不贅述。利用通用有限元軟件建立橋梁計(jì)算模型并進(jìn)行模態(tài)分析，提取結(jié)構(gòu)振型和頻率等模態(tài)信息用于計(jì)算車橋動(dòng)力響應(yīng)。以下重點(diǎn)論述考慮車輛制動(dòng)的車橋耦合振動(dòng)分析模型建立方法和過程。

2.2 考慮車輛制動(dòng)的車橋耦合振動(dòng)分析模型

車輛制動(dòng)過程中，通過輪胎與橋面間的摩擦力使車輛減速，隨車速變化，摩擦力大小不斷改變。定義路面制動(dòng)力與垂直載荷之比為制動(dòng)系數(shù)，其值不僅與路面和輪胎的材料及狀態(tài)有關(guān)，還與它們之間的滑動(dòng)率有關(guān)。為防止剎車時(shí)車輪抱死引起打滑，現(xiàn)多數(shù)車輛已設(shè)計(jì)有防抱制動(dòng)裝置(ABS系統(tǒng))。本文研究對象為裝有ABS的車輛，其制動(dòng)過程可分為2個(gè)階段[10]：1) 常規(guī)制動(dòng)階段：當(dāng)滑移率在0~20%時(shí)，ABS不起作用，車輪未處于抱死滑移狀態(tài)，隨滑移率增加，制動(dòng)系數(shù)逐漸增大；2) ABS控制階段：隨著滑移率提升，系統(tǒng)通過控制和不斷調(diào)整制動(dòng)壓力，將車輪滑移率控制在最佳滑移率20%(對應(yīng)制動(dòng)系數(shù)峰值φ)的附近，防止車輪抱死，使每個(gè)車輪盡可能獲得最大的地面制動(dòng)力。

現(xiàn)將汽車制動(dòng)過程中的制動(dòng)系數(shù)假定為一個(gè)斜坡函數(shù)[11]，即制動(dòng)系數(shù)從0線性地增加至峰值φ，然后保持恒定不變直至汽車在橋上停止或者駛出橋梁，可表示為：

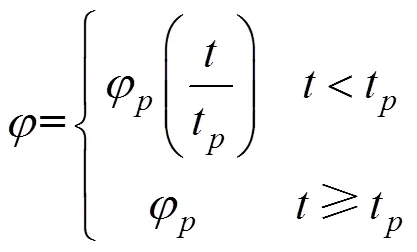
式中：φ為制動(dòng)峰值系數(shù)，其取決于輪胎和路面的種類及使用狀況，另外還與輪胎的結(jié)構(gòu)、氣壓、車速以及運(yùn)動(dòng)狀況有一定的關(guān)系；t為制動(dòng)系數(shù)的上升時(shí)間，s。

車輛制動(dòng)導(dǎo)致的懸架變形和受力情況如圖4所示。當(dāng)車輛制動(dòng)時(shí)，假設(shè)只存在縱向加速度[12]，可建立車體受力平衡方程：

式中：Fzi為第i軸分配得地面反作用力；W為車輛總重；Fxt為地面制動(dòng)力，F(xiàn)xt=Wφ。

假設(shè)車輛簧載質(zhì)量為剛性，各懸架位置受到剛性約束[13]。上述懸架變形可由如下幾何關(guān)系描述：

聯(lián)立式(2)~(4)可得到各軸車輪制動(dòng)力如下：

考慮車輛制動(dòng)作用影響，前述車橋耦合運(yùn)動(dòng)方程可改寫為：

基于上述原理，筆者采用Matlab編制了相應(yīng)的車橋耦合振動(dòng)分析程序，并利用實(shí)橋動(dòng)力試驗(yàn)數(shù)據(jù)對所提出的方法和程序的準(zhǔn)確性和適用性進(jìn)行了驗(yàn)證，結(jié)果表明該方法具有較好的精度，可用于相關(guān)問題的數(shù)值分析研究[14]，過程詳見文獻(xiàn)。

3 汽車制動(dòng)作用下橋梁下部結(jié)構(gòu)動(dòng)力響應(yīng)特征及參數(shù)分析

3.1 汽車制動(dòng)作用下橋墩動(dòng)力響應(yīng)特征

基于所建立的制動(dòng)作用下車橋振動(dòng)分析方法和程序，針對前述橋例及三軸重車，考慮橋面不平度等級為“好”，汽車以初速度50?km/h由車道2駛?cè)霕蛄旱墓r進(jìn)行橋墩動(dòng)力響應(yīng)特點(diǎn)分析。依據(jù)既有研究[15]，普通輪胎的汽車在干燥的柏油或是水泥馬路上制動(dòng)，制動(dòng)系數(shù)峰值φ取值為0.7。制動(dòng)力上升時(shí)間為0.3?s，汽車制動(dòng)后前輪停止在3號墩處，得到各橋墩墩頂動(dòng)力響應(yīng)如圖5所示。

由圖5~6可見，車輛制動(dòng)作用下墩頂縱向動(dòng)力響應(yīng)顯著，豎向和橫向動(dòng)力響應(yīng)幅值較小。汽車開始制動(dòng)后0.3?s內(nèi)處在減速度上升區(qū)段，縱向制動(dòng)力不斷增大，此時(shí)各墩頂縱向動(dòng)力響應(yīng)均逐漸增加；停車瞬間制動(dòng)力消失，相當(dāng)于車輛對橋梁突加反向荷載，此時(shí)橋梁墩頂出現(xiàn)制動(dòng)過程的縱向振動(dòng)加速度極值。此外，支座剛度差異造成不同墩頂處縱向動(dòng)力響應(yīng)存在較大差別，其中2號墩的動(dòng)力響應(yīng)最為顯著。

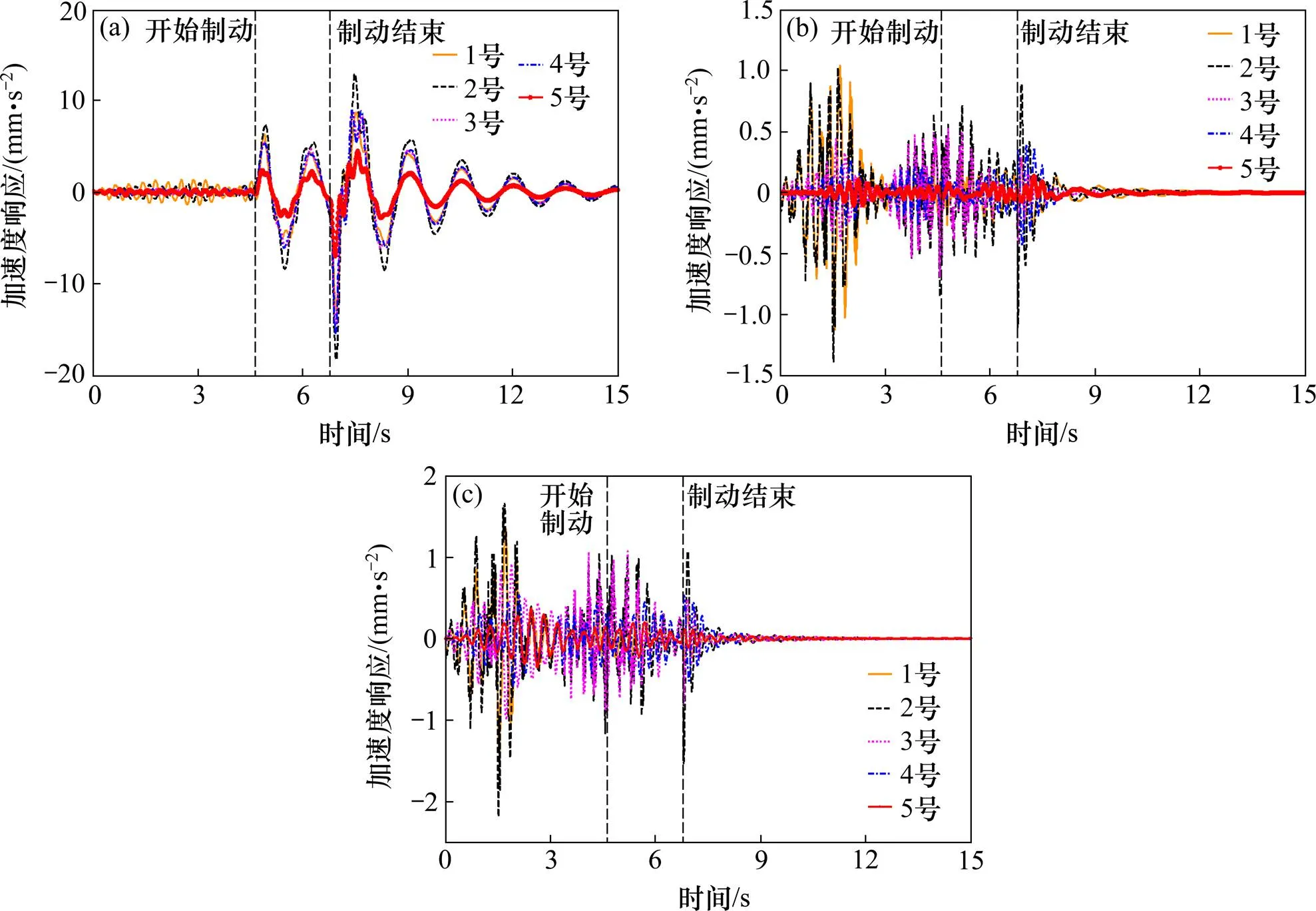
(a) 縱橋向；(b) 橫橋向；(c) 豎向

考慮汽車制動(dòng)的車橋系統(tǒng)動(dòng)力反應(yīng)受多種因素影響，為解釋其影響規(guī)律和機(jī)理，本文將對制動(dòng)車輛的初速度、制動(dòng)力上升時(shí)間、制動(dòng)峰值系數(shù)和車重等關(guān)鍵參數(shù)對墩頂縱向動(dòng)力響應(yīng)的影響開展深入分析。

3.2 車輛初速度的影響

考慮制動(dòng)車輛分別以30，50及70?km/h的初速度駛?cè)霕蛄海渌麉?shù)與3.1節(jié)相同，得到2-1號墩頂縱橋向動(dòng)力響應(yīng)如圖7所示。

由圖7可見，在車輛制動(dòng)停車前，車輛初速度對墩頂縱向動(dòng)力響應(yīng)幅值影響不大；而在制動(dòng)停車后墩頂縱向位移和加速度響應(yīng)幅值受初始速度影響顯著，但無明顯線性規(guī)律。其中初始車速50?km/h對應(yīng)的最大加速度響應(yīng)18.56?mm/s2，較車速為30?km/h和70?km/h增加了73.61%及31.83%，而對于位移響應(yīng)幅值也由50?km/h時(shí)達(dá)到最大，達(dá)到0.7?mm，相比于初始速度為30?km/h及70?km/h時(shí)的位移響應(yīng)峰值分別增加了0.29?mm(68.72%)和0.04?mm (6.40%)。由此可知，制動(dòng)結(jié)束后，相比于位移，墩頂縱向加速度響應(yīng)對車輛制動(dòng)初速度變化更 敏感。

(a) 縱橋向；(b) 橫橋向；(c) 豎向

(a) 縱向加速度；(b) 縱向位移

3.3 制動(dòng)加速度上升時(shí)間的影響

車輛以50?km/h初速度由車道2駛?cè)霕蛄翰⒅苿?dòng)停止在3號墩處，制動(dòng)峰值系數(shù)達(dá)到0.7，分別選取制動(dòng)加速度上升時(shí)間為0.3，1.2，2.1和3?s 4種工況，考察制動(dòng)加速度上升時(shí)間對橋梁下部結(jié)構(gòu)縱向動(dòng)力響應(yīng)的影響。仍以2-1號橋墩頂縱向動(dòng)力響應(yīng)為例予以說明(如圖8)。

由圖8可知，制動(dòng)力上升時(shí)間對墩頂縱橋向振動(dòng)的影響顯著，上升時(shí)間越短橋墩振動(dòng)響應(yīng)越大。其中制動(dòng)力上升時(shí)間0.3，1.2和2.1?s對應(yīng)的加速度峰值響應(yīng)分別較3?s時(shí)增加了56.71%，32.27%和14.60%；對應(yīng)的位移響應(yīng)峰值分別增加了67.55%，12.15%和8.82%。

3.4 制動(dòng)峰值系數(shù)的影響

選取制動(dòng)過程制動(dòng)峰值系數(shù)分別為0.3，0.5及0.7模擬不同的剎車狀態(tài)，橋面平整度等級為“好”，車輛以50?km/h的初速度通過車道2駛?cè)霕蛄翰⒅苿?dòng)停止在3號墩處，制動(dòng)加速度上升時(shí)間均為0.3?s，對比分析2-1號橋墩墩頂縱橋向的動(dòng)力響應(yīng)時(shí)程，如圖9所示。

可見制動(dòng)峰值系數(shù)對橋墩頂縱橋向振動(dòng)有顯著的影響，隨著制動(dòng)峰值系數(shù)增加橋墩振動(dòng)明顯增大。其中當(dāng)制動(dòng)峰值系數(shù)φ=0.5以及φ=0.7時(shí)，相對φ=0.3時(shí)對應(yīng)的加速度峰值和位移峰值分別增加了29.57 %和192.03 %以及68.55%和138.18 %。

(a) 縱向加速度；(b) 縱向位移

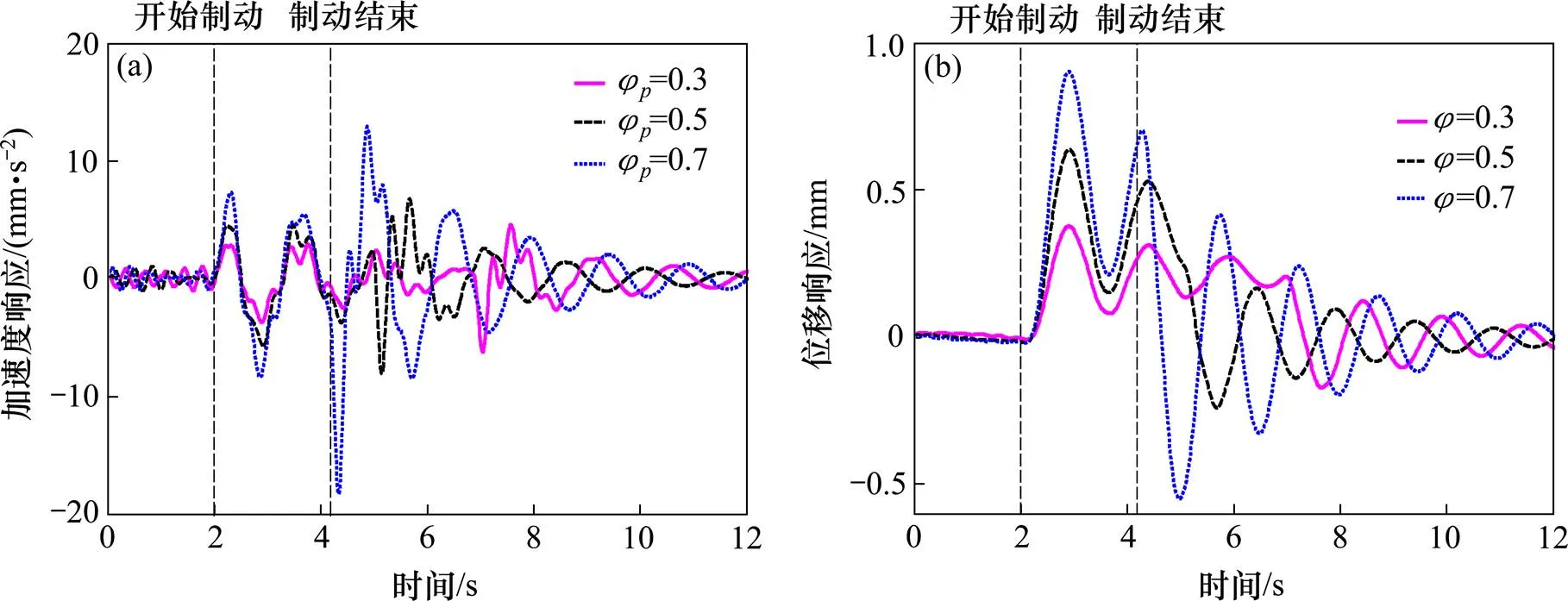
(a) 縱向加速度；(b) 縱向位移

(a) 縱向加速度；(b) 縱向位移

3.5 車重的影響

標(biāo)準(zhǔn)車重(29 802?kg)，1.2倍車重(35 762?kg)，1.5倍車重(44 703?kg)3種工況，橋面平整度等級為“好”，以初速度50?km/h單車由車道2駛?cè)霕蛄翰⒅苿?dòng)停止在3號墩處，制動(dòng)峰值系數(shù)達(dá)到0.7，分析車重對橋梁下部結(jié)構(gòu)縱橋向動(dòng)力響應(yīng)的影響，以2-1號墩為例，結(jié)果見圖10。可見隨著車重由標(biāo)準(zhǔn)車增加到1.2倍和1.5倍車重，墩頂縱橋向加速度峰值分別增加了18.86%和49.86%，位移增加了20.15%和49.98%。表明車重對墩頂縱橋向動(dòng)力響應(yīng)影響明顯，且隨著車重增加，動(dòng)力響應(yīng)顯著增大。

4 結(jié)論

1) 車輛制動(dòng)作用下，橋墩縱橋向動(dòng)力響應(yīng)相對豎向和橫向響應(yīng)更為顯著，適宜作為下部結(jié)構(gòu)狀態(tài)評估的動(dòng)力信號源。

2) 車輛制動(dòng)作用下，初始車速對墩頂縱向動(dòng)力響應(yīng)影響明顯，但無單調(diào)性關(guān)系。

3) 制動(dòng)力上升時(shí)間、制動(dòng)峰值系數(shù)和車重對車輛制動(dòng)作用下橋墩縱向振動(dòng)響應(yīng)均有明顯影響，且該響應(yīng)隨制動(dòng)上升時(shí)間的縮短、制動(dòng)峰值系數(shù)和車重的增大而出現(xiàn)大幅增加。

[1] 殷新鋒, 方志. 車輛制動(dòng)作用下的車輛?路面?橋梁系統(tǒng)隨機(jī)振動(dòng)分析[J]. 計(jì)算力學(xué)學(xué)報(bào), 2010, 27(5): 936? 41. YIN Xinfeng, FANG Zhi. Random vibration analysis of vehicle-pavement-bridge system under vehicle braking[J]. Chinese Journal of Computational Mechanics, 2010, 27(5): 936?941.

[2] 鄧露, 王芳. 汽車制動(dòng)作用下預(yù)應(yīng)力混凝土簡支梁橋的動(dòng)力響應(yīng)及沖擊系數(shù)研究[J]. 湖南大學(xué)學(xué)報(bào)(自科版), 2015, 42(9): 52?58. DENG Lu, WANG Fang. Study of the dynamic response and impact factors of simply-supported prestressed concrete girder bridges due to vehicle braking[J]. Journal of Hunan University (Natural Sciences), 2015, 42(9): 52? 58.

[3] Hoang H P, Pham T D, Pham Q T, et al. Dynamic response of bridge-vehicle three phases interaction considering the effects of sudden heavy braking[J]. International Journal of Advanced and Applied Sciences, 2019, 6(2): 39?47.

[4] 黃進(jìn)鵬, 黃杰忠, 張純, 等. 基于車橋耦合振動(dòng)信號和擴(kuò)展卡爾曼濾波的橋梁結(jié)構(gòu)損傷識別[J]. 土木工程與管理學(xué)報(bào), 2018, 35(5):143?147, 154. HUANG Jinpeng, HUANG Jiezhong, ZHANG Chun, et al. Bridge damage identification based on vehicle- bridge coupling vibration signals and extended kalman filtering[J]. Journal of Civil Engineering and Management, 2018, 35(5): 143?147, 154.

[5] Foti S, Sabia D. Influence of foundation scour on the dynamic response of an existing bridge[J]. Journal of Bridge Engineering, 2011, 16(2): 295?304.

[6] Prendergast L J, Gavin K, Hester D. Isolating the location of scour-induced stiffness loss in bridges using local modal behaviour[J]. Journal of Civil Structural Health Monitoring, 2017, 7(4): 483?503.

[7] NIE Rusong, CHEN Y F, LENG Wuming, et al. Experimental measurement of dynamic load parameters for pier pile caps of high-speed railway bridges[J]. Proceedings of the Institution of Mechanical Engineers Part F Journal of Rail & Rapid Transit, 2015, 231(2): 10?12.

[8] LI Yan, CAI C S, LIU Yang, et al. Dynamic analysis of a large span specially shaped hybrid girder bridge with concrete-filled steel tube arches[J]. Engineering Structures, 2016, 106(1): 243?260.

[9] 李正英, 蔣林均, 李正良. 曲線連續(xù)梁橋支座模型對結(jié)構(gòu)地震反應(yīng)影響分析[J]. 振動(dòng)與沖擊, 2015, 34(2): 182?86. LI Zhengying, JIANG Linjun, LI Zhengliang. Effect of bearing model on the seismic response of curved continuous girder bridge[J].Journal of Vibration and Shock, 2015, 34(2):182?186.

[10] Harifi A, Aghagolzadeh A, Alizadeh G, et al. Designing a sliding mode controller for slip control of antilock brake systems[J]. Transportation Research Part C Emerging Technologies, 2008, 16(6): 731?741.

[11] 姚東強(qiáng), 譚永營, 吳文文. 某型車輛防抱死控制系統(tǒng)設(shè)計(jì)與分析[J]. 山東工業(yè)技術(shù), 2017(21): 24?25. YAO Dongqiang, TAN Yongying, WU Wenwen. Design and analysis of an anti-lock braking control system for a certain type of vehicle[J]. Shandong Industrial Technology, 2017(21): 24?25.

[12] 黃新藝. 混凝土連續(xù)曲線梁橋在車輛荷載作用下的動(dòng)力響應(yīng)研究[D]. 哈爾濱: 哈爾濱工業(yè)大學(xué), 2008: 94?99. HANG Xinyi. Dynamic response research of continuous curved concrete bridges under moving vehicle[D]. Harbin: HarbinInstituteof Technology, 2008: 94?99.

[13] 汪知望, 錢友軍, 郭春雷. 中卡三軸載貨車制動(dòng)系統(tǒng)的匹配設(shè)計(jì)[J]. 合肥工業(yè)大學(xué)學(xué)報(bào)(自然科學(xué)版), 2007, 30(增1): 22?24, 61. WANG Zhiwang, QIAN Youjun, GUO Chunlei. The match design of braking system for a triaxial mid-sized- truck[J]. Journal of Hefei University of Technology, 2007, 30(Suppl 1): 22?24, 61.

[14] 楊婷婷. 基于變速行駛車輛激勵(lì)的橋梁下部結(jié)構(gòu)損傷診斷方法研究[D]. 哈爾濱: 哈爾濱工業(yè)大學(xué), 2019: 18?20. YANG Tingting. Damage detection method for substructure of bridges based on vehicle excitation with variable velocity[D]. Harbin: HarbinInstituteofTechnology, 2019: 18?20.

[15] Gillespie T D. 車輛動(dòng)力學(xué)基礎(chǔ)[M]. 北京: 清華大學(xué)出版社, 2006: 229?231. Gillespie T D. Vehicle dynamics foundational study[M]. Beijing: Tsinghua University Press, 2006: 229?231.

Dynamic performance analysis of substructure for concrete girder bridges under vehicle braking

YANG Tingting1, LI Yan2, LI Quanlin3

(1. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China; 2. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China; 3. Shenzhen Highway Engineering Consulting Company, Shenzhen 518094, China)

The change of the braking coefficient was assumed as a time-varying slope function and the time-varying braking force of each wheel was distributed by using the deformation compatibility condition and force balance equation. Then the vehicle-bridge coupling dynamic analysis model considering braking load was established and the corresponding calculating program was built. Based on a concrete girder bridge, the dynamic behavior of the bridge under the action of vehicle braking was analyzed with the program. The influence factors such as initial velocity, braking acceleration rise time, peak braking factor and vehicle weight on dynamic response of bridge piers were studied. The results show that the longitudinal vibration response of pier top is significantly affected by the braking effect. With the reduction of the braking acceleration rise time, the increase of peak brake factor and vehicle weight, the longitudinal response of the pier increases greatly. The initial velocity has an effect on it, but there appears no linear relationship.

concrete girder bridge; vehicle and bridge coupled vibration; vehicle braking; substructure; dynamic analysis

U441.3

A

1672 ? 7029(2020)03 ? 0637 ? 08

10.19713/j.cnki.43?1423/u.T20190460

2019?05?27

國家自然科學(xué)基金資助項(xiàng)目(51108132)；黑龍江省自然科學(xué)基金資助項(xiàng)目(LH2019E049)

李巖(1978?)，男，黑龍江依安人，副教授，博士，從事橋梁結(jié)構(gòu)振動(dòng)研究；E?mail：liyan2011@hit.edu.cn

(編輯 陽麗霞)