Quasi-symmetry and conserved quantity for generalized Birkhoffian system on time scales

SONG Chuanjing

（School of Mathematics and Physics，SUST，Suzhou 215009，China）

Abstract： In order to reveal the intrinsic relationship between the symmetry and conserved quantity for mechanical systems on time scales，this paper studies the quasi-symmetry and conserved quantity for generalized Birkhoffian system on time scales.Firstly，the differential equations of motion for generalized Birkhoffian system were obtained from the generalized Pfaff-Birkhoff principle on time scales.Secondly，the criteria for quasi-symmetry for this system were investigated.The conserved quantities were given in two cases of whether the time transforms or not.Finally，the results were illustrated.

Key words： quasi-symmetry；conserved quantity；generalized Birkhoffian system；time scale

1 Introduction

Lagrangian mechanics，Hamiltonian mechanics and Birkhoffian mechanics were established one after another[1－2]，where Hamiltonian mechanics plays an important role in non-linear science，Birkhoffian mechanics[3－4]generalized Hamiltonian mechanics，Lagrangian mechanics and Newtonian mechanics，and also applied to quantum mechanics，statistical mechanics，atomic and molecular physics，hadron physics，biological physics，engineering and so on.It is worth noting that generalized Birkhoffian mechanics[5－6]is more significant to study than Birkhoffian mechanics.Because it is easier to construct generalized Birkhoff equations，which also have more degrees of freedom，than Birkhoff equations when the actual problems are taken into account.

In order to unify continuous and discrete analysis，the theory of time scale，which has recently received a lot of attention，was introduced by Stefan Hilger and Bernd Aulbach in 1988[7].Since then，time scale calculus was studied，including dynamic equations on time scales[8－9]，the calculus of variations on time scales[10-13]，Noether theory on time scales[14-22]and so forth.

To better reveal the intrinsic relationship between the symmetry and conserved quantity for mechanical systems on time scales，Noether theorem for generalized Birkhoffian system on time scales is established in this paper.Firstly，the basic definitions and properties of time scale calculus are reviewed.Secondly，generalized Birkhoff equations on time scales are obtained by studying the generalized Pfaff-Birkhoff principle on time scales.Thirdly，quasi-symmetry and conserved quantity are investigated.And finally an example is given to illustrate the results.

2 Time scale calculus and its properties

In this section，we list time scale calculus and its properties briefly.The contents in detail can be seen in Ref.[8-9].

Let T be a time scale，the forward jump operator σ：T→T and the backward jump operator ρ：T →T are defined as σ（t）=inf{p∈T:p＞t}， ρ（t）=sup{p∈T:p＜t}，t∈T，where inf?=supT，sup?=infT.

The forward graininess function μ：T→[0，∞） is defined as μ（t）=σ（t）-t.

The point t is called right-scattered，right-dense，left-dense，left-scattered when σ（t）＞t，σ（t）=t，ρ（t）=t，ρ（t）＜t，respectively.

When T=R，σ（t）=t，μ（t）=0；When T=Z，σ（t）=t+1，μ（t）=1.

When supT＜∞，Tk=T[ρ（supT），supT]；When supT=∞，Tk=T.

Let f：T→R，t∈Tk，if for any ε＞0，there exists N=（t-δ，t+δ）∩T（δ＞0） such that for all ω∈N，the formula

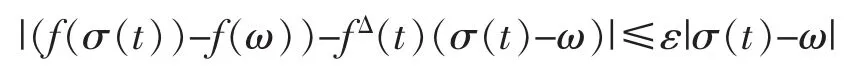
holds，then fΔ（t） is called the delta derivative of f at t.

When T=R，fΔ（t）=f′（t）；When T=Z，fΔ（t）=f（t+1）-f（t）.

The function f：T→R is called rd-continuous if it is continuous at right-dense points and its left-sided limits exist （finite） at left-dense points.The set of rd-continuous functions f：T→R is Crd，the set of differentiable functions f：T→R，whose derivative is rd-continuous，is denoted by

If FΔ（t）=f（t），F(xiàn) is called an antiderivative of f.

Every rd-continuous function has an antiderivative.In particular，if t0∈T，then F defined by F（t）=for t∈T is an antiderivative of f.

There are some other useful properties：

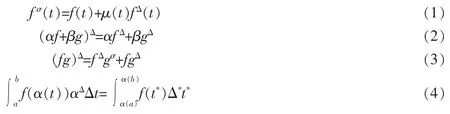
where α:[a，b]∩T→R is an increasingfunction and its image is a new time scale，whose delta operator is denoted by Δ*.

Lemma 1[10]Let g∈Crd，g:[a，b]→Rn，then for allholds if and only if g（t）≡c on [a，b]κfor some c∈Rn.

3 Generalized Birkhoff equations on time scales

Pfaff action on time scales has the form

where Birkhoffian and Bikhoff functionsR×R2n→R aredenotes the delta derivative of ai（t），t∈T，i，k=1，2，…，2n.

Pfaff-Birkhoff principle on time scales can be generalized as

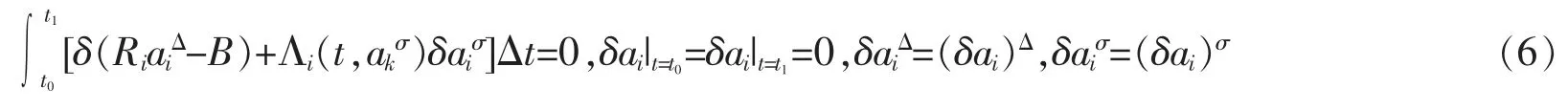
Formula （6） is called generalized Pfaff-Birkhoff principle on time scales.

Expanding formula （6），we have

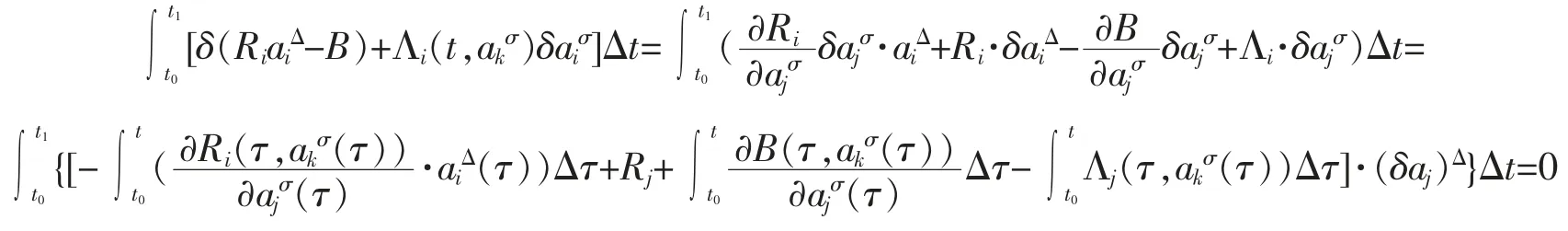
Then from Lemma 1，we get

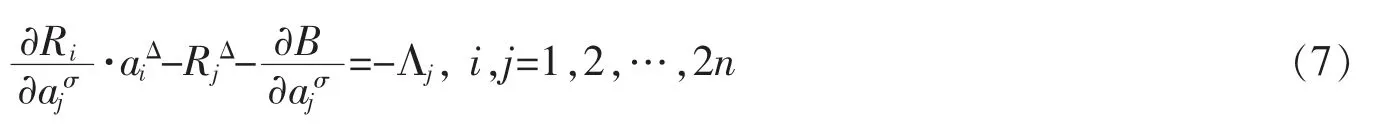
Equations （7） are called generalized Birkhoff equations on time scales.

When T=R，Eqs.（7） become the classical generalized Birkhoff equations[6].If Λj=0，Eqs.（7） become the Birkhoff equations on time scales[19].

4 Quasi-symmetry and conserved quantity on time scales

In this section，the theory of quasi-symmetry and conserved quantity for generalized Birkhoffian system on time scales is established.Conserved quantity is obtained by two steps：first it is considered under the infinitesimal transformations without transforming the time，and second under the infinitesimal transformations with both the time and the coordinates.

The infinitesimal transformations

whose expanding forms are

where ε is an infinitesimal parameter，ξ0and ξiare the infinitesimal generators.

4.1 Conserved quantity without transforming the time

In this section，we assume ξ0＝0.

Definition 1Under the infinitesimal transformations （9），the Pfaff action （5） is said to be quasi-invariant if and only if

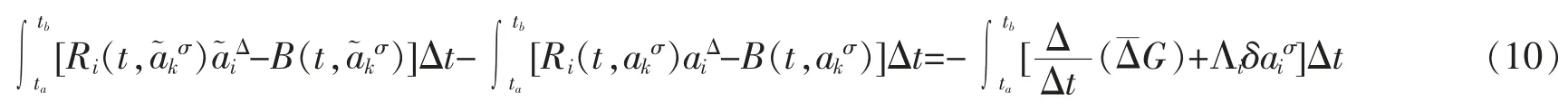
holds for any [ta，tb]?[t0，t1]，ak∈is a gauge function on time scales.

From formula （10），we get

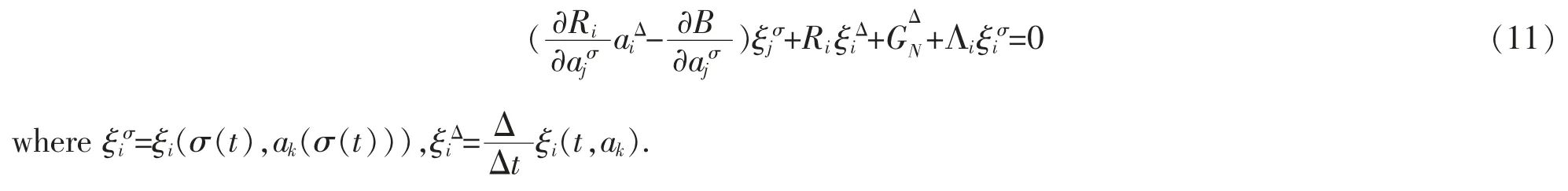
When the Pfaff action is quasi-invariant，the corresponding infinitesimal transformations are called quasisymmetrical transformations，and quasi-symmetry can be verified from the quasi-symmetrical transformations.Hence，formula （11） is the criterion of quasi-symmetry on time scales.

Definition 2A functionis said to be a conserved quantity for the generalized Birkhoffian system on time scales if and only if

holds along all the solution curves of the generalized Birkhoff quations （7）.

Therefore，we have

Theorem 1For the generalized Birkhoffian system （7），if there exists a gauge function GNsuch that the generators ξisatisfy the formula （11），then a conserved quantity exists for this system as follows

Proof.From Eqs.（7） and formula （11），we have

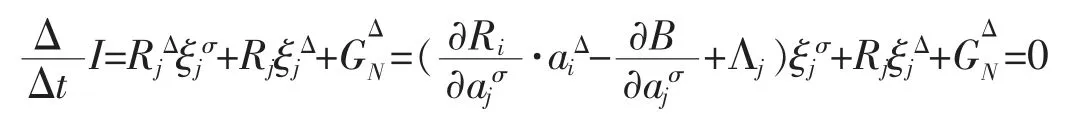
This proof is completed.

4.2 Conserved quantity with transforming the time and the coordinates

In this section，we assume ξ0≠0.

Definition 3Under the infinitesimal transformations（9），the Pfaff action （5） is said to be quasi-invariant if and only if for any

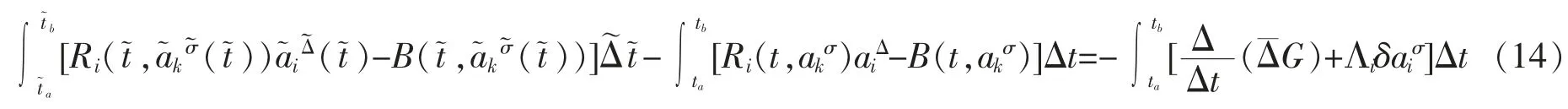
Hence，from formula （14），we can get the criterion for quasi-symmetry on time scales

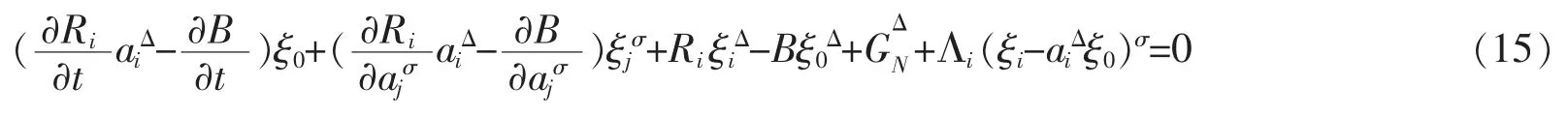
Formula （15） is called Noether identity for generalized Birkhoffian system on time scales.

Then we have

Theorem 2For the generalized Birkhoffian system （7），if the Pfaff action （5） is quasi-invariant under the infinitesimal transformations （9），then there exists a conserved quantity for this system

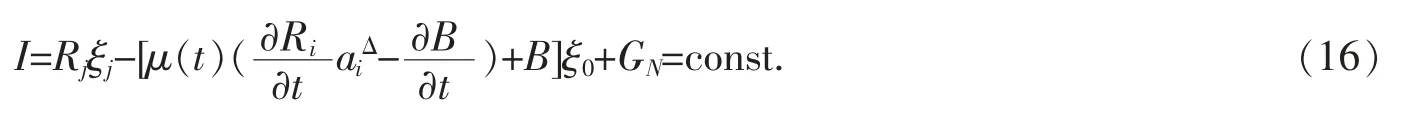
Proof.We plan to convert the quasi-invariant under Definition 3 into the quasi-invariant under Definition 1，then use Theorem 1 to complete this proof.

Denoting

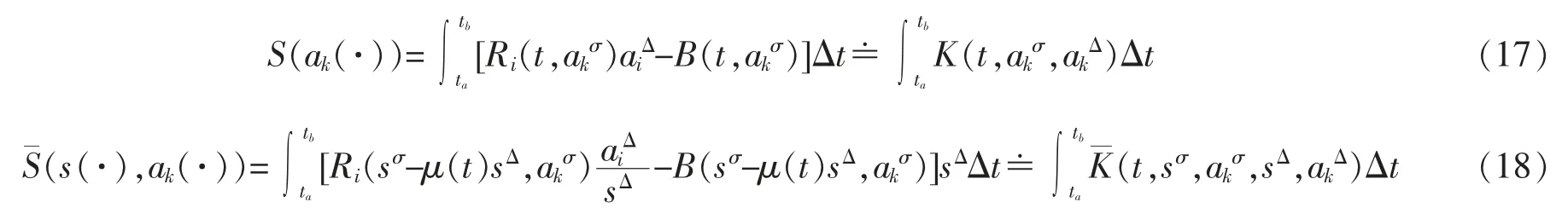
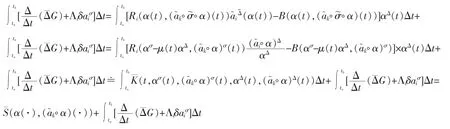
Under the condition of s（t）=t，noting

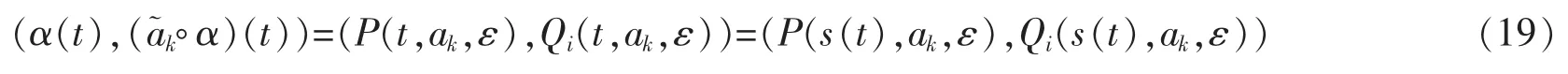
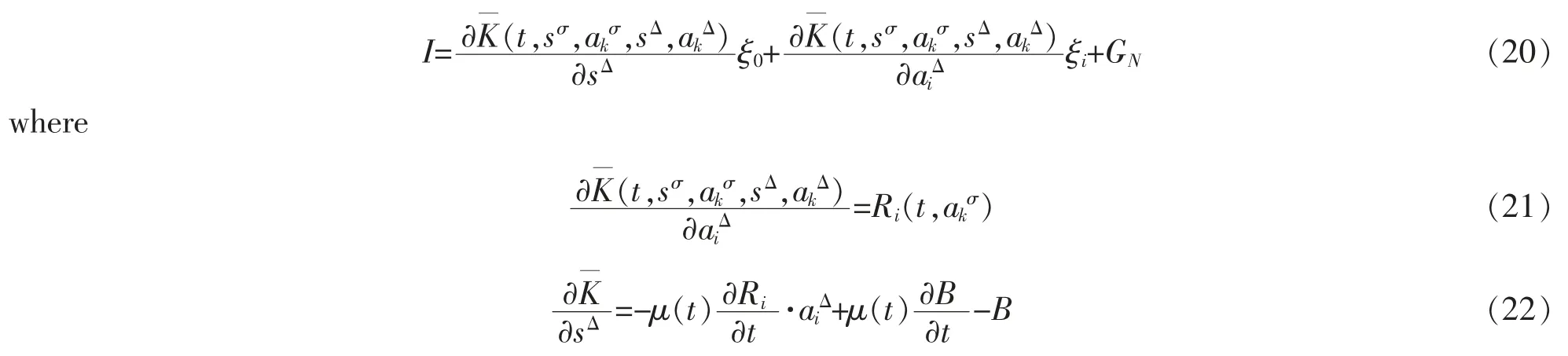
from formulae （20）-（22），we can get the intended result.

Remark 1When T=R，we can get the Noether identity and conserved quantity for the classical generalized Birkhoffian system[6].

Remark 2When GN=0，Λj=0，we can get the Noether identity and conserved quantity for the Birkhoffian system on time scales[19].

5 Example

Let T={2n:n∈N∪{0}} and

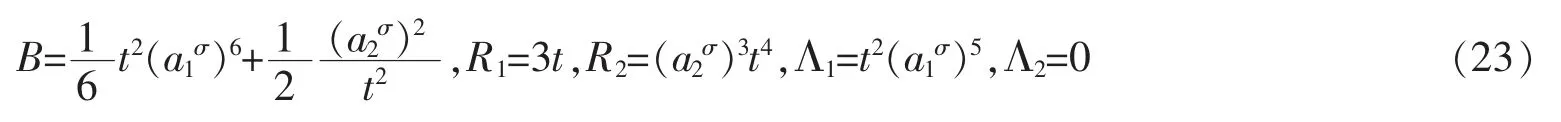
Try to find out its quasi-symmetry and conserved quantity.

From the Noether identity （15），we have

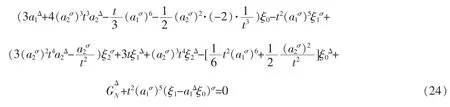
Taking calculation，we get

Theorem 2 gives

6 Conclusion

Based on the generalized Pfaff-Birkhoff principle on time scales，generalized Birkhoff equations and conserved quantity are obtained for the generalized Birkhoffian system on time scales.Birkhoffian system on time scales and the classical generalized Birkhoffian system are special cases of this paper.Considering the integers Z is also a time scale，discrete generalized Birkhoff equations and discrete conserved quantity can undoubtedly be deduced from this paper.Furthermore，Lie symmetry method and Mei symmetry method are also important modern integral methods.Hence，it is hoped that they can also be used to find conserved quantity for the generalized Birkhoffian system on time scales.