高斯波對阻抗邊界下離軸球形粒子的聲輻射力

臧雨宸， 冀瑾皓

（1.中國科學院 聲學研究所，北京 100049；2.中國科學院大學 物理科學學院，北京 100049）

與電磁場一樣，聲場攜帶有一定的動量。 當聲波與物體發生相互作用時會產生反射、吸收等現象，往往會伴隨著動量的轉移。因此，物體受到了聲場的力的作用，稱為聲輻射力。聲輻射力的概念自提出以來，便迅速引起了聲學界的重視，并在醫學超聲、材料科學和航天工業等領域得到了越來越廣泛的應用。 1969 年，彈性粒子的聲輻射力計算被Hasegawa 等人順利完成[1]。 1990 年，J Wu 等人計算得到了聚焦波束下粒子的聲輻射力[2]。 進入21 世紀以來，關于粒子所受聲輻射力的研究方法又有了重大突破。 2005 年，F G Mitri 等人嘗試計算得到了平面駐波聲場和類駐波聲場下柱形粒子的聲輻射力特性[3]。 2006 年，J Lee 等人利用聲線理論，研究了流體介質中任意位置的聲輻射力特性，并驗證了所謂“聲捕獲力”的可能[4]。 2009 年，F G Mitri 等人計算了貝塞爾聲束對剛性球的聲輻射力[5]。 2011 年，Silva 等人將其擴展到任意波束，大大拓寬了粒子所受聲輻射力的應用范圍[6]。2013 年，陳東梅等計算了高斯波束對水中球形粒子的聲輻射力[7]，宋智廣等計算了高斯波束對水中柱形粒子的聲輻射力[8]。 2017 年，喬玉配等在自由空間的基礎上增加了阻抗邊界，得到了此時柱形粒子的聲輻射力，并嘗試討論了粒子與邊界距離大小等因素對聲輻射力的影響[9-10]。 然而，縱觀已有的研究結果，大多數結論基于粒子位于聲軸的情形，這大大限制了有關理論的實際應用。 筆者基于聲波的散射理論，通過有限級數法將高斯波束展開為球函數的形式，推導得到了阻抗邊界下高斯波束對于離軸球形粒子的聲輻射力公式，繪制剛性球和液體球的聲輻射力函數曲線，并討論了頻率、粒子與邊界距離、束腰半徑和離軸角度與距離等各因素對聲輻射力函數的影響。

1 理論

考慮半徑為a 的球形粒子位于理想流體中的阻抗邊界附近，粒子中心到邊界的距離為d。 根據鏡像原理可知，邊界的存在可以等效為在其另一側存在鏡像波和鏡像粒子，鏡像粒子與邊界的距離也為d。 一束高斯波沿z 軸正方向傳播。以小球球心為原點O，高斯波束束腰中心的坐標為（0，y0，z0）。同時，以鏡像小球的球心為另一坐標原點建立鏡像坐標系圖1 為此時的物理模型。

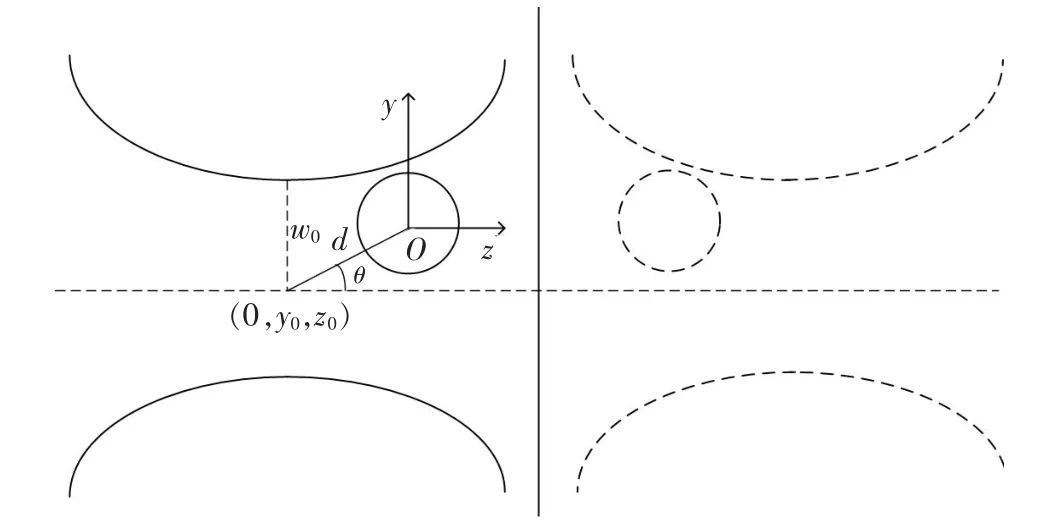
圖1 阻抗邊界下離軸球形粒子的聲散射示意圖

1.1 波束因子的計算

嚴格來講，高斯波束的波陣面并不是一個平面，但是在束腰附近，可以近似作為平面來處理。入射高斯波束的速度勢函數表示為

式中：φ0為速度勢的幅值，k 為波數，w0為高斯波束的束腰半徑，此處略去時間因子。 設

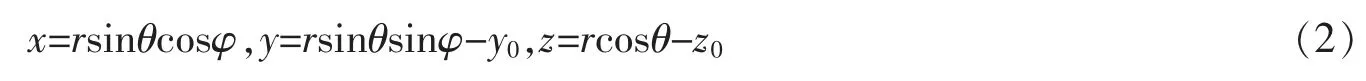
在yoz 平面內，φ=0，上式可以簡化為

將高斯波束在球形粒子的中心處按照球函數進行級數展開

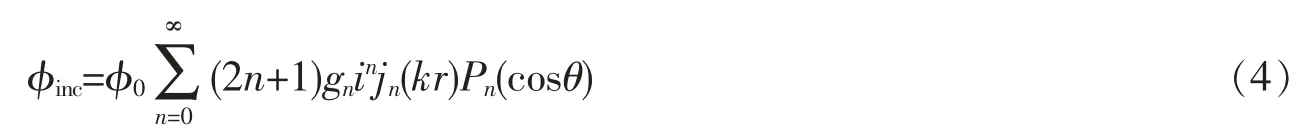
式中： jn(·)為n 階第一類球貝塞爾函數，Pn(·)為n 階勒讓德函數，r 為球坐標系下的徑向坐標，gn為入射高斯波束的波束因子。 參照在軸高斯波束中波束因子的計算方法[11]，可以得到，當n 為偶數時，波束因子為

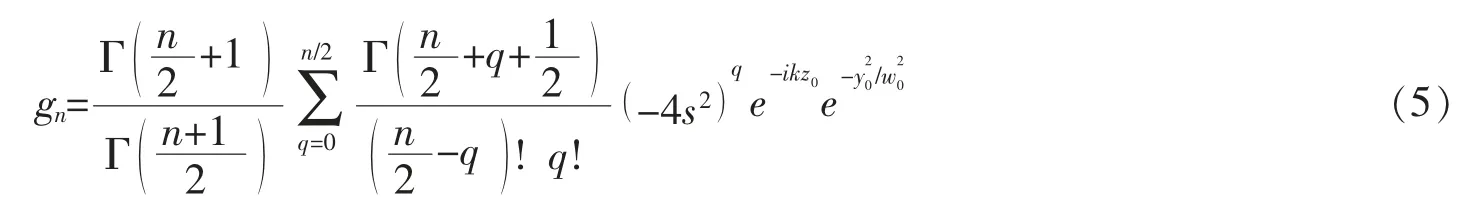
當n 為奇數時，波束因子為

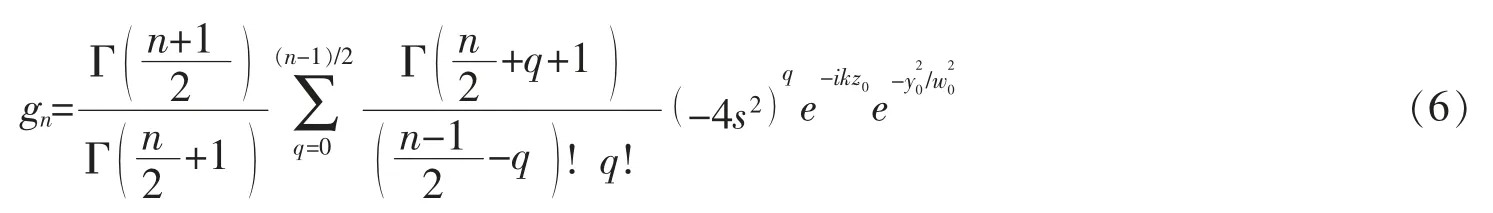
式中：s=1/kw0。

1.2 散射系數的計算

得到了波束因子，可以用它來表示空間中存在的所有聲場。 阻抗邊界的反射波在坐標系（r，θ，φ）中可以表示為

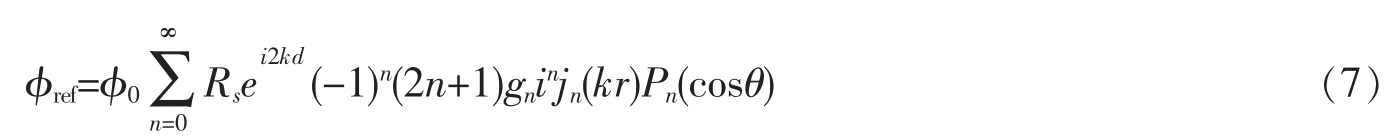
式中：Rs為邊界的聲壓反射系數。

球形粒子的散射波在坐標系（r，θ，φ）中可以表示為

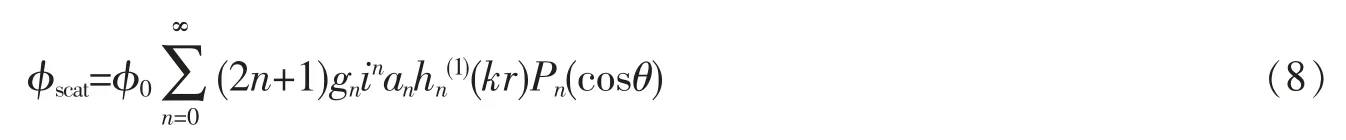
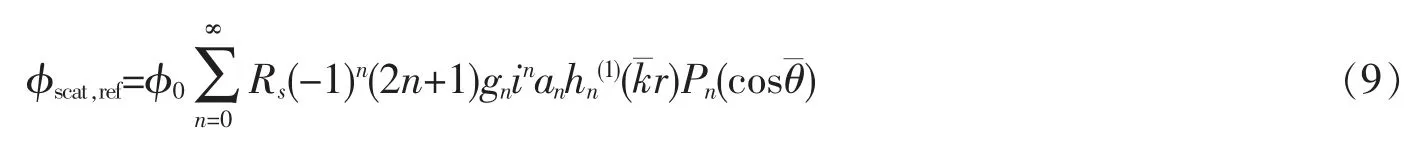
如果粒子材料的聲阻抗足夠大，表面可以看成剛性邊界，則粒子內部不存在聲波，表面徑向速度為零，即

為了利用邊界條件求得散射系數，首先利用球函數的加性定理將鏡像粒子的散射波改寫為

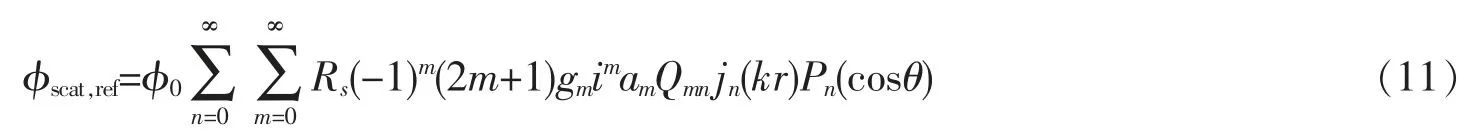
式中：Qmn的表達式可以在參考文獻[12]中找到。

綜合上述各式，可以得到聲場中的總速度勢為

引入如下定義

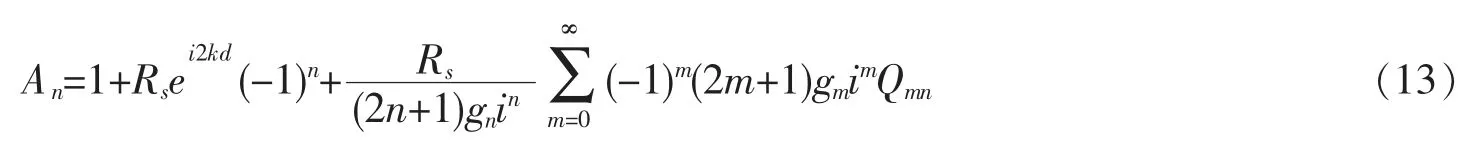
則式（12）可以整理為

再根據速度勢與質點速度的關系，得到徑向速度表達式為

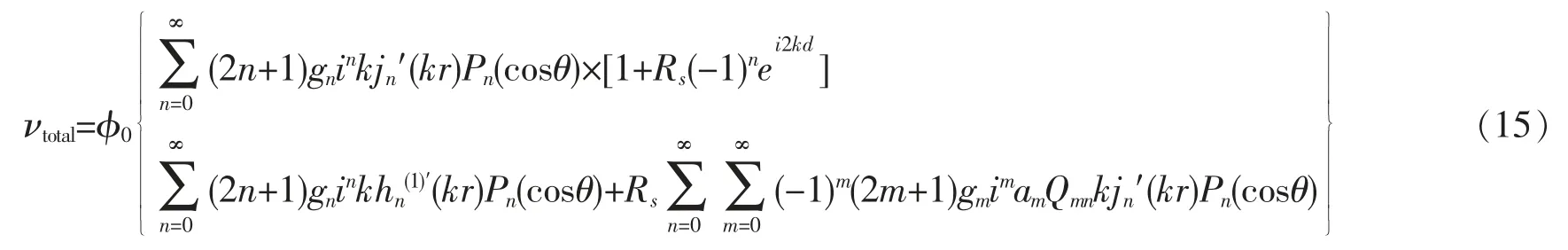
由式（15）和邊界條件（10）可以得到散射系數an。

如果粒子材料的聲阻抗不滿足表面剛性的邊界條件，則必須考慮粒子內部折射波的存在，其速度勢可以寫成

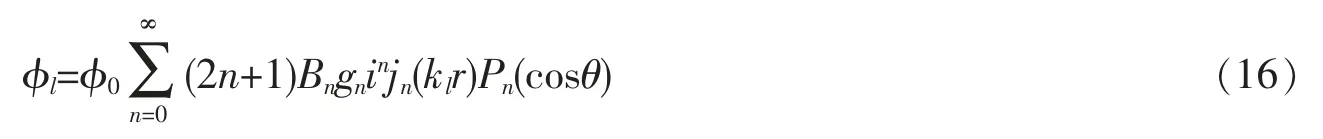
式中：Bn為折射波速度勢的幅值，依賴于粒子表面的邊界條件。 此時式（8）顯然不再成立，應以表面處聲壓和徑向速度連續取代之，即

式中：pl和νl分別表示折射波的聲壓和速度勢。 式（17）中各量皆可以很容易地通過速度勢函數求得，這里不再贅述。 根據此組邊界條件，可以計算出an和Bn。

1.3 聲輻射力的計算

理想流體中粒子所受的聲輻射力可以表示為[1-10]

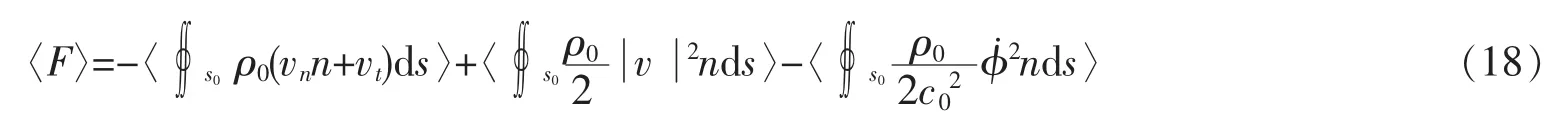
式中：vn和vt分別為法向和切向速度分量，ρ0為流體介質的密度，c0為流體介質中的聲速。

根據式（18），可以得到在聲波傳播方向的聲輻射力為

式中：ψ=Re（φtotal）。

將式（12）代入，計算可得軸向聲輻射力可以表示為

式中：E 為聲波的空間能量密度，S 為球形粒子的橫截面積，Yp為聲輻射力函數，表示單位能量密度和單位橫截面積所受到的聲輻射力大小，其表達式為

2 數值模擬

根據式（23）可以進行入射高斯波束對阻抗邊界下離軸球形粒子的聲輻射力的數值仿真。 假設粒子周圍的流體介質是水，且將水看成理想流體。在液體球形粒子的情況下，假定粒子內部充滿油酸。水和油酸的相關聲學參數見表1。

表1 水和油酸的相關聲學參數

2.1 不同邊界反射系數下的聲輻射力函數曲線

假定束腰寬度w0=3λ，粒子中心與束腰中心的距離d0=λ，d0與z 軸的夾角θ=π/6。在粒子與阻抗邊界距離d0=2a 的情況下，對不同反射系數下粒子在聲場中受到的聲輻射力函數進行仿真，結果如圖2 所示。 圖2（a）和2（b）分別顯示了剛性球和油酸球的聲輻射力函數隨ka 的變化曲線。 可以看出，不論是剛性球還是油酸球，聲輻射力在ka 比較小時變化較劇烈。 值得一提的是，在某些頻率處可以出現負向的聲輻射力，此時粒子會被聲波向聲源的方向吸引。在ka 比較大時，聲輻射力在一個穩定值附近出現小幅振蕩，這是由于粒子的散射波和邊界的反射波之間復雜的干涉現象所引起的必然結果。 隨著反射系數的增大，聲輻射力的峰值減小，但振蕩峰值的位置并不因此而改變。對比圖2（a）和2（b）可以發現，油酸球的聲輻射力峰值遠小于剛性球，且其峰值位置也有所不同。

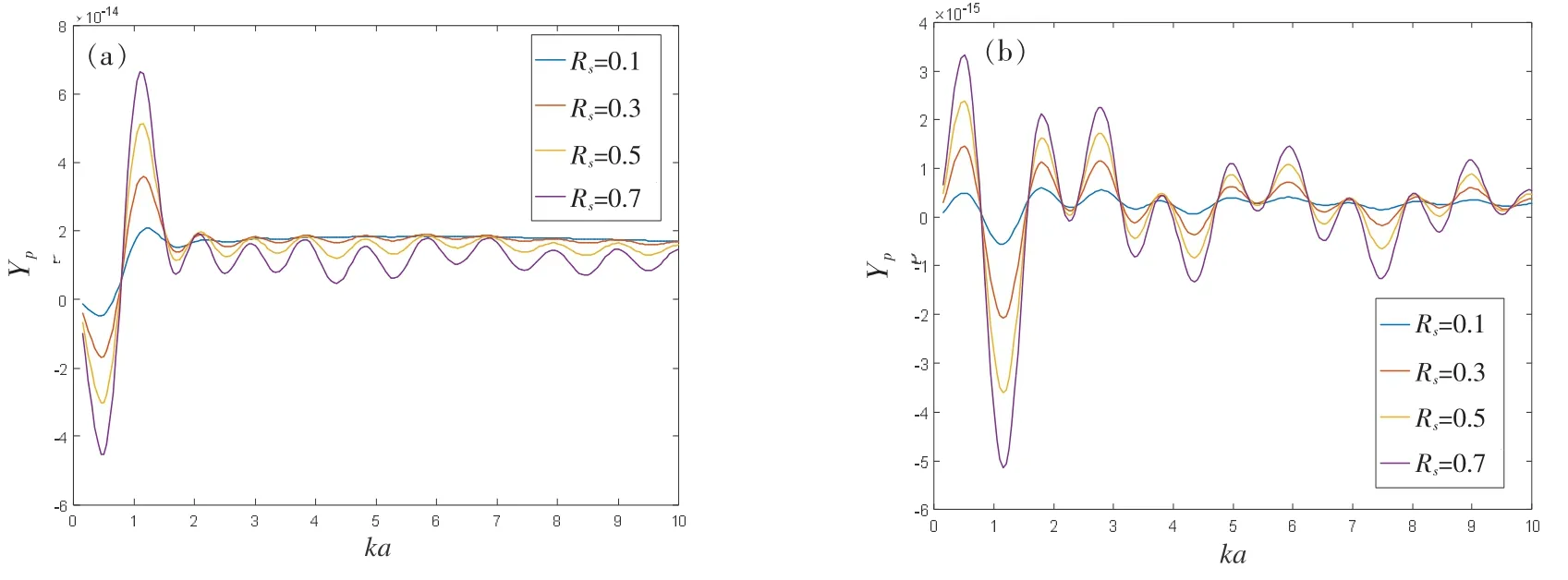
圖2 不同反射系數下聲輻射力函數Yp 隨ka 的變化

2.2 粒子與邊界的距離對聲輻射力的影響

假定束腰寬度、粒子中心離軸的距離和角度均保持不變，ka=0.5，對不同反射系數下剛性球和油酸球所受的聲輻射力隨kd 的變化進行仿真，結果分別如圖3（a）（剛性球）和3（b）（油酸球）所示。可以發現，在ka 固定時，聲輻射力函數隨kd 的變化類似于正弦曲線，呈現出明顯的周期性，并且聲輻射力函數的峰值隨著反射系數的增大而增大，但反射系數的改變并不影響曲線的周期。對比圖3（a）和3（b），油酸球的聲輻射力函數周期與峰值都小于剛性球。 這些和2.1 中得到的結論是一致的。

2.3 束腰半徑對聲輻射力的影響

為研究高斯波束的束腰半徑對于聲輻射力的影響，固定邊界的聲壓反射系數Rs=0.5，粒子與邊界的距離d=2a，粒子中心離軸的距離和角度不變，對不同束腰半徑下的聲輻射力進行仿真，剛性球和油酸球的結果分別如圖4（a）（剛性球）和4（b）（油酸球）所示。 仿真的結果表明，束腰半徑對于聲輻射力的影響主要體現在ka>2 時，即中高頻附近。 隨著束腰半徑的增加，中高頻處的聲輻射力函數在不斷增大，并且最終趨近于平面波入射的情況。

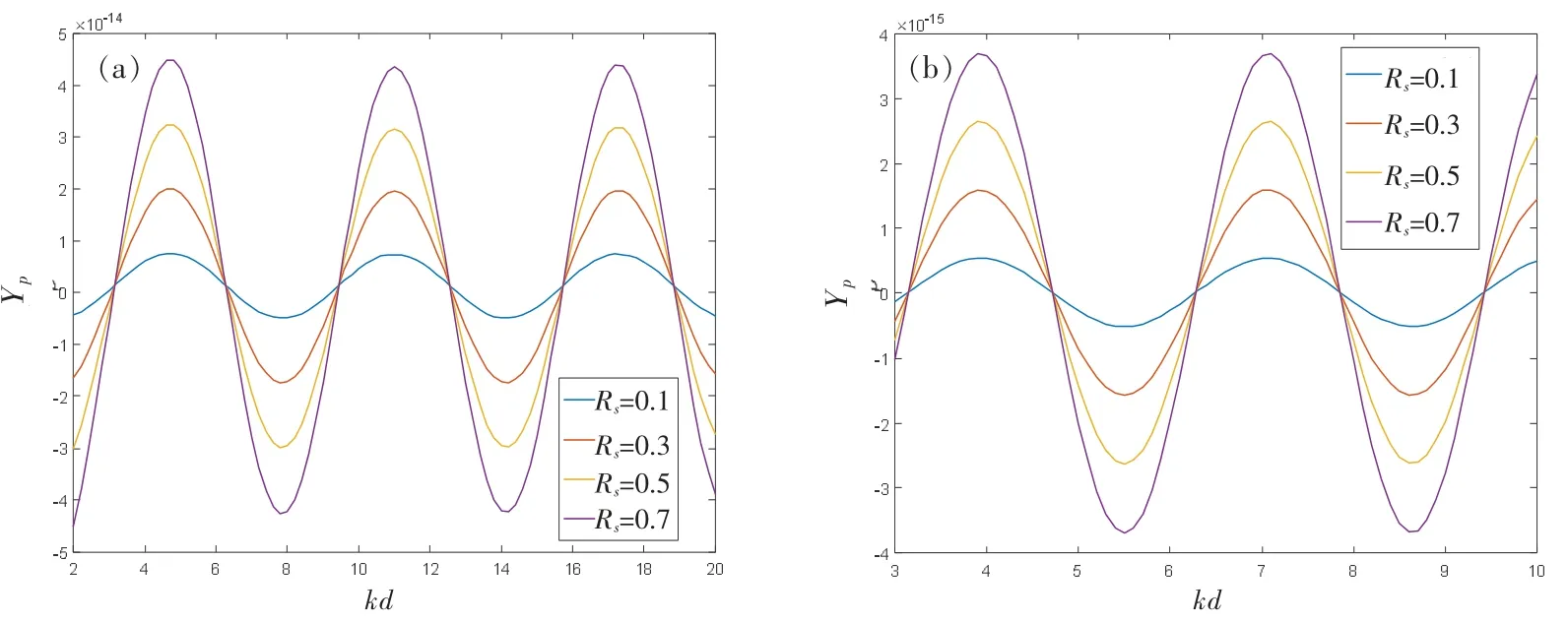
圖3 不同反射系數下聲輻射力函數Yp 隨kd 的變化

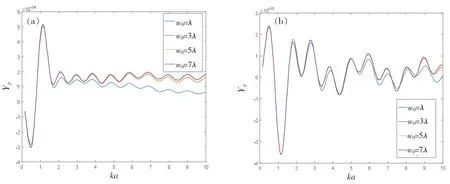
圖4 不同束腰半徑下聲輻射力函數Yp 隨ka 的變化

2.4 離軸距離與角度對聲輻射力的影響

在粒子中心偏離傳播軸時，離軸的距離與角度對于聲輻射力顯然是有影響的。 固定ka=0.5，邊界的聲壓反射系數Rs=0.5，粒子與邊界的距離d=2a，束腰寬度w0=3λ。 為了討論方便，采用無量綱量kd0作為橫坐標。當d0與z 軸的夾角變化時，分別繪出其聲輻射力函數隨kd0的變化曲線，剛性球和油酸球的結果分別如圖5（a）和5（b）所示。 從中可以看出，無論d0與z 軸成何種角度，聲輻射力函數的幅值都隨kd0的增大而減小。 另一方面，當kd0固定時，聲輻射力函數隨θ 的增加而減小，并且當θ 較大時，聲輻射力函數將以更快的速度衰減到零。 這些結論都是與直觀相符的。

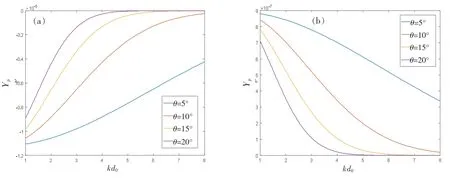
圖5 不同角度下聲輻射力函數Yp 隨kd0 的變化

3 結語

計算了阻抗邊界下高斯波束對球形粒子的聲輻射力。 該文從聲波的散射理論出發，根據鏡像原理以及高斯波束的級數展開理論，結合球函數的加性定理，推導出了阻抗邊界下高斯波束對于球形粒子的聲輻射力解析表達式。在此基礎上，對不同參數下剛性球和油酸球的聲輻射力進行了數值仿真。仿真的結果表明，聲輻射力函數在中低頻處變化較快，在適當的頻率處存在負向聲輻射力的現象。 邊界聲壓反射系數的改變會影響聲輻射力函數的峰值，但不影響取峰值時的ka 大小。當其他因素保持不變時，聲輻射力函數隨粒子與邊界的距離呈現周期性，且反射系數的變化并不改變曲線的周期。 束腰半徑是描述高斯波束的重要特征，其對聲輻射力函數的影響主要體現在中高頻，當束腰半徑不斷增大，曲線越來越趨近于平面波的情形。 最后，粒子中心偏離傳播軸的距離和角度對聲輻射力函數曲線有著顯著影響，距離越大，角度越大，聲輻射力微弱。 此外，在相同的條件下，剛性球的聲輻射力遠大于油酸球。 文中的結果預期可以為實際的聲操控和聲學鑷子的制備提供理論指導。