大規模MIMO系統中動態遷移導頻分配

卞寶銀，付 凱，史燕平，李秀彩，黃 鑫，韓東升

（1.南瑞集團有限公司（國網電力科學研究院有限公司），南京 211006； 2.南瑞集團有限公司智能電網保護與運行控制國家重點實驗室，南京 211106； 3.華北電力大學 電氣與電子工程學院，河北 保定 071003）

0 引 言

大規模多輸入多輸出（Multiple－Input Multiple－Output，MIMO）通過在基站端配置成百上千根天線陣列，在相同時頻資源上同時與多個用戶進行通信，極大地提高了頻譜效率。Marzetta指出當基站天線趨于無窮時，高斯噪聲以及互不相關的小區間干擾將消失，用戶的性能將僅取決于用戶所受到的導頻污染［1］，通常在相鄰小區間使用正交導頻來避免來自第一層干擾小區的導頻污染［2］，但會減小服務的用戶數目。協調相鄰小區間的導頻分配可以有效減少導頻污染，如基于圖著色的導頻分配方案［3－4］、基于人工魚群算法［5］和遺傳算法［6］的導頻配置方案，然而這些方案的計算復雜度都較高。對小區內的用戶進行分組，將相鄰小區使用相同導頻的用戶控制在較遠的范圍內來減小相鄰小區的導頻干擾，可以有效地改善導頻污染［7－9］。

雖然上述方案針對導頻資源的合理分配可以取得較為理想的系統性能，但是當用戶移動速度較快時，相干時間塊的減小會使系統更加頻繁地進行導頻重分配，增加了計算復雜度。為此，本文提出了一種動態遷移導頻分配算法，該算法在兩個時隙之間僅針對移動幅度較大的用戶進行額外的導頻優化，選擇一個用戶與之交換導頻，對于其他的用戶不改變其導頻。相對于傳統算法，由于僅針對移動幅度較大的用戶，所以可以有效地降低計算復雜度。

1 系統模型

考慮一個時分雙工（Time Division Duplex，TDD）多用戶大規模MIMO系統，系統中有L個小區，每個小區配備一個有M 根天線的基站，基站位置在小區的中心位置。假設所有的基站性能相同，每個基站最多可以服務K個用戶，每個用戶配備一根接收天線。每個小區的用戶分為中心區域用戶組和邊緣區域用戶組，每個小區的中心區域用戶組復用同一組正交導頻，邊緣區域用戶使用另一組正交導頻，這兩組正交導頻之間相互正交。

基站與用戶間的信道狀態信息（Channel Status Information，CSI）由大尺度衰落和小尺度衰落的疊加來表示［10］。用hjlk∈瓘M表示基站j與第l個小區中的第k個用戶之間的信道狀態信息，有

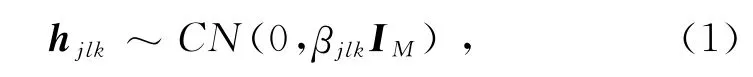
式中：CN（0，R）為零均值的循環對稱復高斯分布，R為協方差矩陣；βjlk為信道衰落方差；IM為M階單位陣。βjlk＝C／rαjlk，C 為固定參數；α 為路徑損耗指數；rjlk為第l個小區內第k個用戶與基站j之間的距離。

時頻資源塊被分解成一個包含Tcs和WcHz的幀，亦即S＝TcWc為每一幀所發送的符號數，假設Tc小于等于所有用戶的相干時間，Wc小于等于所有用戶的相干帶寬。B＞1是每一幀需要額外發送的導頻序列。剩下的S－B為數據發送的時頻塊，可將其分為上行數據發送塊和下行數據發送塊。

在上行鏈路中，采用一種統計感知的功率控制策略［11］。在小區l（該小區部署基站j）中，用戶k的發送功率可以表示為plk＝ρ／βjlk，式中，ρ＞0為功率設計因子，如果把噪聲功率記為σ2，那么系統的 接 收 信 噪 比 （Signal to Noise Ratio，SNR）為ρ／σ2。

1.1 導頻發送階段

設導頻信號占據每幀的B（1≤B≤S）個符號，每個導頻信號可以用一個B×1維的向量v來表示，且每個導頻符號的功率均相同。可令導頻符號的歸一化幅度為1，有｜［v］s｜＝1，［］s為向量的第s（s∈ ｛1，2，3，.…，B｝）個元素。所有正交導頻序列來自一個固定的集合V＝｛v1，…，vB｝，集合V 是一個B×B的矩陣，其中的每一個列向量表示一個導頻向量，且任意列向量滿足

設基站j接收到的導頻信號為Yj，據此對信道向量hjlk進行最小均方誤差估計，得到的信息向量為＾hjlk，

1.2 數據發送階段

基站根據已經得到的CSI進行信號檢測以及預編碼運算，由于大規模MIMO信道的近似正交特性，可以很容易地區分出不同用戶發送的數據。

基站j的上行接收信號為yj，設該基站所屬小區的索引也為j，用（j，k）表示小區j中的用戶k，（j，k）的上行可達頻譜效率SEjk可以用式（3）來表示［11］，SINRjk為小區j中用戶k的信干噪比。

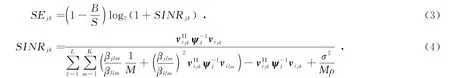
當M → !時，式（4）可以化簡成式（5）：

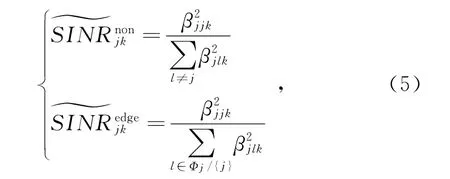
由式（5）可知，當M →!時，系統的性能僅受限于導頻污染，而導頻污染取決于使用相同導頻的用戶大尺度衰落的和與此用戶的大尺度衰落的比值，而信道的大尺度衰落僅與距離有關，因此合理地分配使用相同導頻用戶之間的距離可以有效降低導頻污染的影響，提高系統性能。

2 動態遷移導頻分配算法

文獻［8］的導頻分配算法將用戶分成中心用戶組及邊緣用戶組，對中心用戶復用同一組導頻，邊緣用戶使用正交導頻，可以有效地改善邊緣用戶所受到的干擾，相較于貪婪算法可以有效地降低系統復雜度。

雖然傳統的導頻分配算法在降低導頻分配復雜度方面做出了大量努力，但是對于算法的改進僅針對單次的導頻分配算法，而降低不同時隙間導頻分配算法的復雜度卻鮮有研究。

假設服務用戶數目始終處于飽和狀態且不發生改變，如果確定了中心用戶（或邊緣用戶）與總用戶數目的比值be，中心用戶和邊緣用戶的數量也將保持不變，只是用戶的位置會隨時間隨機改變。當一個用戶的位置變化超出了它本身所在的分組范圍并對系統產生了較大的影響時，這種變化將成為用戶的遷移。實際上，如果兩個用戶的優先級相同，且使用相同的通信協議與基站進行信號傳輸，那么新舊用戶的交替也可以看成是用戶位置的變化。我們也將這種變化稱為用戶遷移，所以用戶遷移包括用戶位置的移動以及新舊用戶的交替。

在用戶遷移的過程中，需要重新使用導頻分配算法來適應用戶的變化，這會增加導頻分配的計算復雜度。為了降低計算復雜度，針對遷移用戶的導頻分配問題，本文提出了一種動態遷移導頻分配算法。遷移狀態模型如圖1所示。用Class表示用戶的遷移狀態，Class＝1表示位于某小區中心位置的用戶遷移至本小區的邊緣區域；Class＝2表示位于某小區邊緣區域的用戶遷移至相鄰小區的邊緣區域；Class＝3表示位于位于某小區中心位置的用戶遷移至相鄰小區的邊緣區域；Class＝4表示某小區中心位置的用戶遷移至相鄰小區的中心區域。

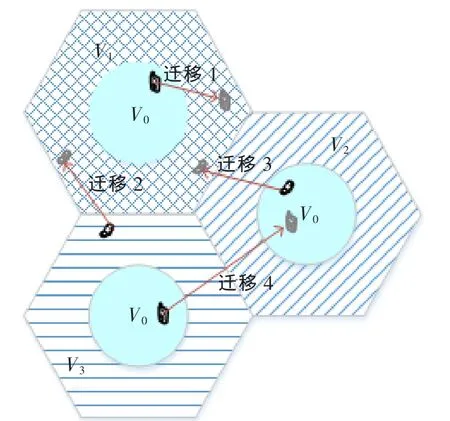
圖1 用戶遷移模型

對于Class＝1，從上一時隙定義為邊緣區域的用戶中選擇一個信道狀態最好的用戶強制遷移至中心區域用戶組。遷移1的反狀態即位于某小區邊緣區域的用戶遷移至本小區的中心區域（可記為Class＝－1），對此采用相似的處理方法，從上一個時隙定義為中心區域的用戶中選擇一個信道狀態最差的用戶強制遷移至邊緣區域用戶組。兩個遷移的處理方式相似，不再對他們進行詳細區分介紹。對于遷移3也作類似的處理，遷移2和遷移4沒有反狀態。

對于Class＝2，對上一個時隙的導頻分配不做任何變化。

對于Class＝3，處理方法類似于遷移1，首先在該小區的邊緣用戶組中尋找一個信道狀態較好的用戶強制遷移至中心用戶，然后遷移用戶與之交換導頻。需要注意的是，由于導頻組V1、V2和V3是相互正交的，所以即使用戶遷移至相鄰小區的邊緣區域，也可以看作是遷移到了本小區的邊緣區域來處理，也就是說，即使它的位置轉移到了相鄰小區，仍可以選擇原來位置小區的基站請求服務，并使用其為之分配的導頻。

對于Class＝4，可以分解成一個遷移3和一個遷移1的反向，對它進行遷移3和遷移1的兩次遷移處理即可。

通過對以上4種遷移情況的分析，針對不同的遷移狀態，選擇一個用戶與遷移用戶交換導頻，稱這個被交換的用戶為替代用戶。更為形象一點的說明是，每一個用戶總是希望自己使用的是正交導頻，即被分組到邊緣用戶組。考慮到導頻數目的有限性，一旦一個用戶離開邊緣用戶組，那么一定會在本小區內形成一種競爭，以決定究竟哪一個用戶來代替這個位置。選擇這個替代用戶時，通常需要考慮以下兩個因素：（1）這個替代用戶必須是接近邊緣用戶組的用戶，也就是在地理位置上離中心位置較遠；（2）這個替代用戶的導頻分配給遷移用戶后，遷移用戶所受的干擾最小，也就是遷移后的用戶與替代用戶的干擾用戶之間距離較遠。綜合分析以上兩點我們采用的具體策略如下：

（1）確定導頻遷移前后的位置信息以及用戶的遷移類型（假設Class＝－1）；

（2）從本小區的中心用戶組中找出ks（ks＜K×be）個距離中心較遠的用戶，將這ks個用戶定義為待選用戶組；

（3）比較這ks個待選用戶的干擾用戶與遷移用戶之間的距離和Dk，Dk最小的待選用戶設為替代用戶，Dk＝（uk，j－uk，l）2，uk，l為用戶（l，k ）的位置。

稱上述選擇替代用戶的具體策略中的第3點為替代準則。綜上，針對Class＝－1的基于用戶跟蹤的動態導頻分配算法流程如圖2所示。

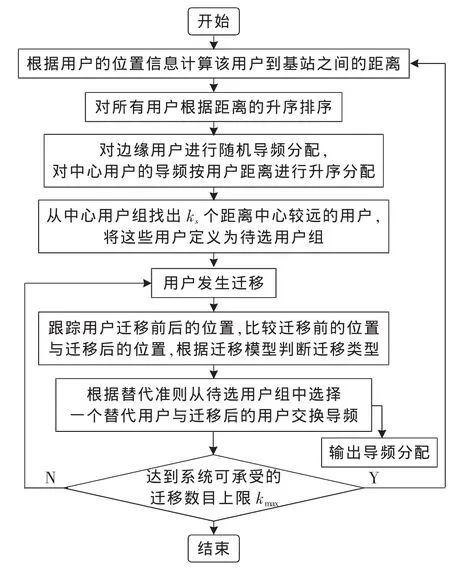
圖2 動態導頻分配算法流程圖

階段一（在首個時隙）

步驟1：根據用戶的位置信息計算該用戶到基站之間的距離dk，j；

步驟2：對各用戶根據dk，j的升序排序，距離較小的K×be個用戶定義為中心用戶組Unon，j，其他用戶定義為邊緣用戶組Uedge，j，第K×be個用戶的值定義為閾值dth，j；

步驟3：對Unon內的用戶進行隨機導頻分配，對Uedge用戶的導頻按用戶大尺度衰落升序分配；

步驟4：從中心用戶組中找出ks個距離中心較遠的用戶，將這ks個用戶定義為待選用戶組；

階段二（用戶發生遷移后）

步驟5：跟蹤用戶 （k，j）遷移前后的位置，比較遷移前的位置（uk，j）與遷移后的位置（uk，j′），根據遷移模型判斷遷移類型；

步驟6：根據替代準則從待選用戶組中選擇一個替代用戶與遷移后的用戶交換導頻；

步驟7：用戶再次發生遷移后，重復步驟5～6，

步驟8：達到系統可承受的遷移數目上限kmax后，重復步驟1～8。

針對Class＝1的導頻分配算法與Class＝－1時相似，只是構建的待選用戶組不同，Class＝1時的待選用戶組是邊緣用戶組中ks個距離中心較近的用戶，稱此待選用戶組為邊緣待選用戶組，Class＝－1時的待選用戶組為中心待選用戶組。Class＝2時不進行額外的導頻分配，Class＝3與Class＝－1時的待選用戶組一致，只是需要遷移后用戶所在小區的中心待選用戶組，顯然Class＝－3與Class＝1時的待選用戶組一致。當Class＝4時需要同時調用兩個待選用戶組，遷移前小區的邊緣待選用戶組以及遷移后小區的中心待選用戶組分別按照替換準則選出替換用戶1和替換用戶2，遷移用戶先與替代用戶1進行導頻交換，之后再與替代用戶2進行導頻交換。依照本算法，如果發生的遷移為遷移1或3，那么需要進行一次動態遷移導頻分配；發生遷移2不需要進行額外的導頻分配；發生遷移4需要進行兩次動態遷移導頻分配。假設4種遷移發生的概率相同，平均發生一次遷移引起一次動態遷移的導頻分配。

3 復雜度分析

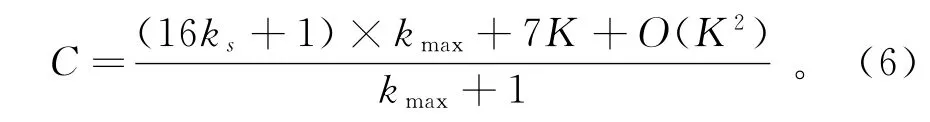
由式（6）可知，除第1個時隙外，其他時隙的計算復雜度都與用戶數目K無關，而僅與待選用戶的數目ks及最大遷移數目kmax有關。系統的復雜度隨著ks的增大而增大，隨著kmax的增大而減小。表1給出了K＝20時算法復雜度對比。由表可知，本文算法復雜度較低，與傳統算法相比具有明顯優勢。

本文采用浮點數flop進行復雜度分析，一個加號代表一個實浮點數操作，一個乘號代表兩個實浮點數操作。計算一次距離的復雜度為7，一次排序的算法復雜度為O（K2），將用戶距離較近的Ko個用戶分成一組，其余的Ke個用戶分成一組，然后再進行導頻分配。整個導頻分配過程包括K 個用戶距離計算以及1次排序計算，所以傳統算法的復雜度總計為7 K ＋O（K2）。

本文提出的算法在第1個時隙與傳統算法是一致的，第1個時隙的運算復雜度為7 K＋O（K2）。從第2個時隙開始不再對所有的用戶進行排序，而是針對發生了遷移的用戶，先判斷用戶的遷移類型，然后根據遷移類型從待選用戶組中選擇一個替代用戶進行導頻交換。判斷遷移類型的平均用戶復雜度為2，計算Dk的運算復雜度為15，求最大（小）值需要比較ks－1次，其運算復雜度為ks－1，總計運算復雜度為2＋15×ks＋ks－1＝16×ks＋1。假設系統平均每個時隙發生一次遷移，達到系統最大遷移數目的時間為kmax個時隙，平均每個時隙的運算復雜度為

表1 K＝20時算法的復雜度對比

4 仿真結果與分析

假設有3個相互相鄰的小區，基站位于小區的中心區域，基站的坐標分別為（0，0），／2，3r／2）和（－／2，3r／2），r為小區半徑，這3個基站都配備有M 根天線，每個基站最多可以服務K個用戶，且服務的K個用戶隨機出現在服務范圍內的任意位置。具體的仿真參數如表2所示。

表2 仿真參數

導頻的長度τ與K以及導頻的分配策略be有關，具體來說滿足τ＝K×be＋K×（1－be）×3。假定在兩個相干塊之間必定存在用戶發生遷移，這是因為沒有發生用戶遷移的時隙不進行導頻的重新分配，故而忽略這些時隙。在下一個時隙，隨機選取一個用戶，它的位置隨機遷移至這3個小區范圍內的任意位置。

圖3～6分別對比了3種不同算法下，系統的頻譜效率與SNR、M、單位小區用戶數目K以及be的變化曲線。這4個圖中3種算法頻譜效率的變化趨勢均相同，且本文所提算法的性能介于傳統導頻分配與隨機導頻分配之間，并且接近傳統的導頻分配算法。

圖3 不同SNR下的導頻分配算法性能比較曲線圖

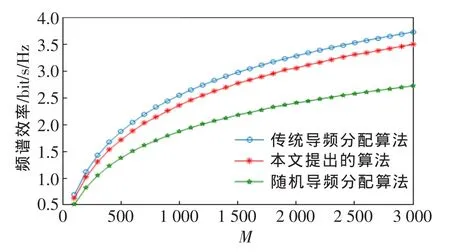
圖4 不同M 下的導頻分配算法性能比較曲線圖

圖5 不同K下的導頻分配算法性能比較曲線圖

圖3中，當一個用戶的位置發生遷移時，相較于傳統的導頻分配算法，單位用戶的平均頻譜效率大約降低了0.2bit／s／Hz，遠高于隨機導頻分配算法的性能。圖4也驗證了用戶遷移后單位用戶的平均頻譜效率降低了0.2bit／s／Hz的這一結論，并且不會因為M的增加而擴大差距。而隨機導頻分配卻會更早地進入瓶頸。這表明，隨著M 的增加，合理地導頻分配可以有效地延緩頻譜效率因為導頻污染而停滯不前的現象。隨著用戶數目的增加，導頻污染的影響也隨之增加，單位用戶的頻譜效率隨之下降，由圖5可知，隨著用戶數目的增加，單位用戶的遷移對系統頻譜效率的影響隨之減小，可以預見，此時系統能夠承受更多的遷移用戶。由圖6可知，當be較小即導頻富足時，導頻分配算法沒有明顯的優勢；當be較大即導頻緊缺時，導頻分配的優勢表現明顯。注意到當be的值為1時，所有小區復用同一組導頻，此時將只會存在第3類遷移，其概念也與小區切換無異。小區的頻譜效率隨著be的變化先上升后下降，并在be＝0.5時達到最大值。

圖7所示為遷移用戶數目對算法性能的影響曲線圖。由圖可知，本文所提算法的曲線整體呈下降趨勢，并且斜率越來越小。但即使遷移用戶的數目超過單位小區用戶數目后，本文所提算法效率仍然高于隨機導頻分配算法，這體現了對小區進行分組后再進行導頻分配的固有優勢，即使遷移用戶多于用戶數目時，系統的平均頻譜效率仍然存在一定的優勢。假如以3.6作為基準，那么系統可承受的遷移數目為7。

圖7 遷移用戶數目對算法性能的影響曲線圖

5 結束語

本文針對多用戶大規模MIMO網絡，考慮導頻資源分配在不同時隙間再分配問題，以用戶遷移模型表征系統拓撲結構的變化，提出了一種動態遷移導頻分配算法，復雜度分析及仿真結果表明，本算法相較于傳統的導頻分配算法可以顯著地降低計算復雜度，并且與傳統的導頻分配算法具有相近的頻譜效率。因此，在多個時隙之間，使用導頻交換算法可以以犧牲少量頻譜效率為代價有效地降低復雜度。