土體應力狀態分析及水壓力計算

宋 征

(三峽大學 科技學院，湖北 宜昌 443002)

0 引 言

應力狀態和強度理論在工程中有著較為廣泛的應用，土體的應力狀態也常用于分析土力學各類復雜的問題[1～3].土壓力的計算是支擋結構設計的主要內容，經典理論的簡化條件使得計算結果誤差較大，如朗肯理論忽略墻背摩擦導致主動土壓力計算結果偏大，庫倫理論僅適用于無黏性土等，本研究以二向應力狀態為基礎，分析了經典土壓力理論計算結果在應力狀態中的區別，并根據滲透力的定義對水土壓力的計算進行了思考，指出了黏性土合算在應力狀態中的不合理性，結合本方法，考慮孔隙率和滲流影響時主動土壓力與水土分算與合算的結果，并進行了對比分析.

1 土體二向應力狀態

實際土體的應力狀態是十分復雜的，為便于分析，常取圖1所示二向應力狀態.根據材料力學的結論，一定深度微元土體內傾角為α斜面上的正應力和切應力為,

(1)

(2)

土體的破壞主要是因為剪切破壞引起，若土體微元體內傾角為α斜面上的切應力剛好達到土體剪切極限狀態，則傾角α即為該深度最危險滑動面切線的傾角(破裂面).假定土體極限時符合莫爾-庫倫強度準則[4]：

τ=c+σtanφ

(3)

將式(1)、(2)帶入(3)式可得,

(4)

式中，c為黏聚力，/KPa;φ為土體內摩擦角,/°.

高度為H的支擋結構主動土壓力合力大小為,

2 二向應力狀態求解經典理論土壓力的應用

2.1 忽略切應力的朗肯土壓力理論

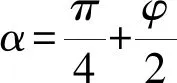
(5)

式中，γ為土體重度，/(KN/m3);z為計算點到填土表面深度,/m.將式(5)代入式(4)可得,

即得朗肯主動土壓力計算表達式.

2.2 考慮墻背摩擦的庫倫土壓力理論

庫倫理論假定墻后為無黏性土體，將破裂面內土體視為剛體，從靜力平衡的角度進行分析，同時考慮了墻背摩擦的影響.當擋墻豎直、填土表面水平時，無黏性土庫倫理論主動土壓力計算表達式為[5]，

式中，δ為墻背摩擦角，/°.

若墻背粗糙，則切應力τxy≠0，極限狀態時將式(4)作以下變換,

(6)

代入式(4)整理后可得,

σx=A·γz-B·c

(7)

式中,A、B為與破裂面傾角相關的無量綱參數.

在庫倫理論條件下，擋墻豎直、填土水平時極限破裂角αcr為,

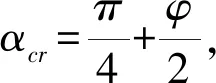
式(6)退化為朗肯主動土壓力計算表達式.

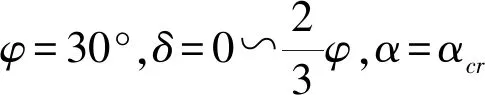
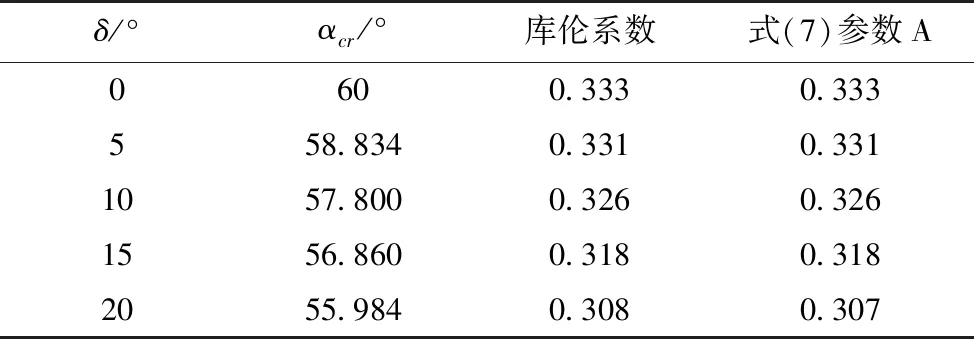
表1 參數A與庫倫系數的對比(φ=30°)

從表1計算結果可見，當取α=αcr時，式(7)參數A值與庫倫主動土壓力系數一致，若以無黏性土(c=0)計算，則式(7)退化為無黏性土庫倫主動土壓力計算表達式.

2.3 考慮地震情況的M-O法

Mononobe-Okabe法(以下簡稱M-O法)是以庫倫理論為基礎，考慮地震作用的擬靜力分析方法.擋墻豎直、填土表面水平時，無黏性土M-O主動土壓力計算表達式為[6]，

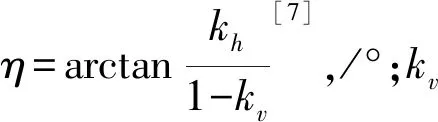
墻后土體在地震作用下相應應力會發生變化，豎向地震作用影響σy，水平地震作用影響τxy，將式(4)作如下變換,

(8)

將式(8)帶入式(4)整理可得,

σx=D(1-kv)·γz-F·c

(9)

式中,D、F為與破裂面傾角和地震角相關的無量綱參數.

為對比分析，設豎直擋墻高H=6 m，填土水平，墻后土體無黏性(c=0)，γ=20 kN/m3，φ=30°，δ=15°，不同地震情況計算結果如表2所示.

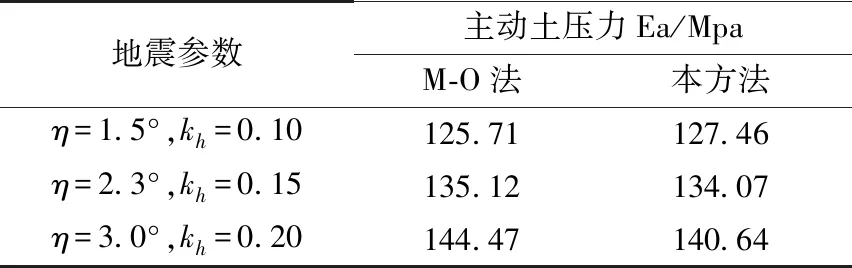
表2 不同地震參數對主動土壓力影響

從表2結果可以看出，在地震角或水平地震系數影響下，本方法主動土壓力與M-O法較為接近，忽略計算誤差的影響，可以認為在較小地震參數情況下，式(9)退化為M-O法主動土壓力計算表達式.對于地震參數較大時，M-O法主動土壓力計算結果較本方法大.

3 二向應力狀態下水土壓力的思考

支擋結構上土壓力和水壓力的計算，在《建筑基坑技術支護技術規程》[8](以下簡稱《規程》)中，推薦砂性土以有效應力原理為基礎的水土分算，而黏性土因孔隙水壓力的計算困難采用總應力法的水土合算，均質土的表達式為，

水土分算：

(10)

水土合算：

(11)

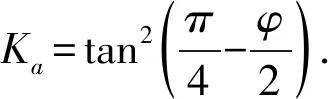
砂性土分算時取有效指標即浮重度γ′，有效內摩擦角φ′和有效黏聚力c′；黏性土合算時取總應力指標，即地下水位以下飽和重度γsat，固結不排水指標φcu和ccu.

水土合算未考慮孔隙和滲流影響，存在理論缺陷[9]，相關學者對分算與合算的統一算法進行了研究[10～12]，以孔隙水壓力乘某個系數后將分算與合算的結果連續化，仍然存在黏性土合算缺乏理論依據的問題.

地下水不流動時的水壓力為靜水壓力，式(10)中u=γwh(γw為水的重度，h為計算點至地下水位高)；地下水流動時，土體受到滲透力的作用，對于滲透力的定義和對土體的影響，相關學者分別提出了自己的看法[13～15]，本研究比較傾向于李廣信在文獻[13]中的定義：“土骨架受到的滲透水流施加的推動力與拖曳力稱為滲透力”，蔣中明等[16]也明確了滲透力由推動力和拖拽力組成，并指出均為面力，而計算中滲透力作為體積力也是一種等效的面力.綜上所述，當土體受流動地下水作用時，應該以土骨架為研究對象，作用在土骨架上滲透力的大小為[13,16]：

J=γwi=nγwi+(1-n)γwi

(12)

式中，i為水力梯度，n為孔隙率.

根據滲透力的定義，式(12)中的nγwi為拖拽力，(1-n)γwi為推動力.將土骨架假定為圖1所示應力狀態，在朗肯理論假定條件下，推動力作用骨架水平方向，拖拽力作用剪切方向，將(4)式作以下變換，

(13)

帶入式(4)，并取i=-?h/?z[15]整理可得，

σx=cotαtan(α-φ)γ′z-

cosφ/sinαcos(α-φ)c+U

(14)

式中，U(KPa)為滲流影響的應力增量.

(15)

該式即為水土分算計算表達式(10).

若根據本方法推導水土合算(11)式，則需要在朗肯理論條件下將(4)式作如下變換，

即推動力作用豎直方向，但需以總應力換算，這就違背了滲透力作用于土骨架的定義(土骨架受到的應該為有效應力)，同樣說明了水土合算的理論缺陷.

綜上所述，黏性土滲流作用下的水土壓力計算，合算方法并不合理，可按照式(14)進行計算分析.以式(4)為基礎，在不同條件下的變換如表3所示.

表3 黏性土水土壓力計算變換

4 水土壓力算例分析

設擋墻高H=10 m，墻背豎直填土水平，地下水位于填土表面，飽和重度γsat=18 kN/m3，水重度γw=10 kN/m3，有效指標φ′=30°，c′=0 Mpa，總應力指標φcu=29°，ccu=5 Mpa，孔隙率n=0.487，根據《規程》的水土分算和水土合算及本方法計算，結果如圖2所示.

從圖2可以看出，水土分算的結果是偏大的，而水土合算結果沒有考慮孔隙率的影響.本方法計算公式中孔隙率的大小影響土壓力，計算結果介于分算和合算之間，若考慮滲流影響，擋墻內外水位差越大，則滲透力越大，式(14)中U越大，作用擋墻的主動土壓力也就越大.

算例是以朗肯理論條件為基礎，若考慮地震、墻背摩擦等情況，則只需按表3將式(4)式進行變換，若計算曲面破裂面土壓力，則將式(4)中的傾角α按實際計算點曲面傾角代入.

5 結 論

本研究分析了墻后填土二向應力狀態，基于莫爾-庫倫準則推導了擋墻主動土壓力計算表達式，通過與經典理論對比分析，說明了應力狀態在土壓力計算中的應用，并就水土壓力計算進行了思考，通過算例分析得出以下結論：

1)二向應力狀態分析可作為土壓力分析的基礎，根據實際考慮的因素，將(4)式進行變換即可得到不同情況下支擋結構的土壓力.

2)土壓力的計算與切應力τxy取值有關，當τxy=0時，本計算結果與朗肯理論一致；當τxy=σxtanδ時，本計算結果與庫倫理論一致.較小地震角時，本計算結果與M-O法較接近，較大地震角時，M-O法偏大.

3)滲透力的定義決定了水對于土體的作用需要以土骨架為研究對象，滲透力的正向推動力和切向拖拽力會影響土骨架的應力狀態.

4)水土壓力計算中，黏性土的合算缺乏理論依據，而分算值偏大，本研究結果介于分算和合算之間，并考慮孔隙率和滲流的影響，與實際情況較接近.

5)本方法可以計算平面破裂面情況下的土壓力，也可以按實際情況中最危險滑動曲面進行分析，僅需在式(4)中進行相應變換.