多隨機障礙物條件下AGV動靜態路徑規劃研究
唐 龍,肖 翠,呂宣宣,劉有余
(安徽工程大學 機械與汽車工程學院,安徽 蕪湖 241000)
自動導引運輸車(Automated Guided Vehicle,AGV)最早用于運載貨物,隨著信息技術的發展,其應用領域也在不斷擴展。其中,路徑規劃作為AGV的基礎功能,是實現其尋優路徑及自主避障的關鍵,一直是學者們研究的熱點。目前,國內外比較成熟的是針對已知環境的全局路徑規劃方法。文獻[1-2]利用改進粒子群算法,避免陷入局部最優;文獻[3]利用改進螞蟻算法,加快收斂速度;文獻[4-5]引入柵格地圖,建立了直觀的環境模型。針對未知動態環境,主要是通過傳感器獲取局部環境信息,進而將外界信息傳給中央控制器,進而做出避障行為;文獻[6]結合勢場法和蒙特卡羅定位法,使機器人避開動態障礙物;文獻[7]利用模糊邏輯控制在動態環境下規劃出全局較優路徑。這些方法主要針對勻變速運動,但對于非勻變速物體的避障效果不是很理想。
結合上述方法,首先建立環境與AGV的數學模型,基于粒子群算法,規劃靜態環境;針對非勻變速物體,引入逐步判別法,對隨機障礙物逐一判別避障,進而實現多隨機障礙物環境的路徑規劃。
1 靜態環境的路徑規劃
1.1 建立環境模型
針對AGV運行環境,采用柵格[4]模擬固定障礙物,利用平面坐標系規劃地圖,建立AGV的運行環境模型。為了便于計算仿真,將AGV簡化為一個質點,同時擴大固定障礙物的邊界尺寸,實際上是把AGV的實際尺寸和排斥區域Ⅰ折算進障礙物的面積里。
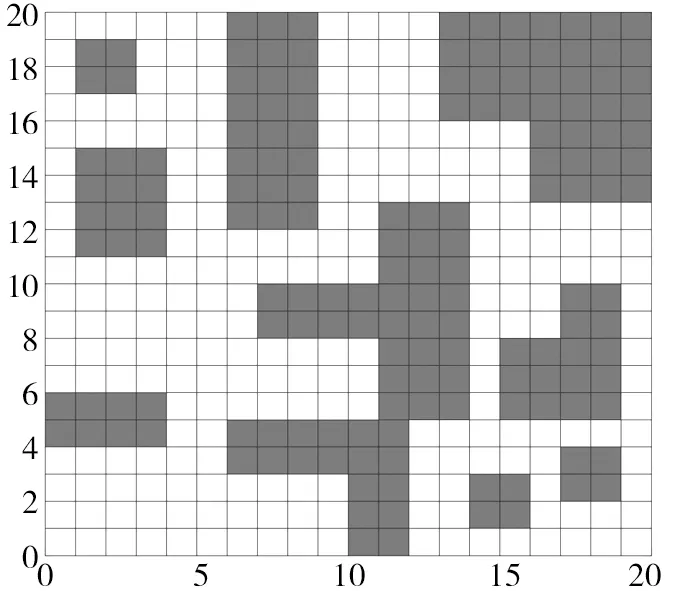
圖1 柵格地圖
柵格地圖如圖1所示。對柵格地圖作了以下定義:黑色柵格為障礙柵格,白色柵格為自由柵格;不滿一個柵格時算一個柵格;把地圖的邊界當成障礙物來處理。
1.2 路徑規劃步驟
(1)輸入由0和1組成的矩陣,構建柵格地圖(0表示自由域,1表示障礙物)。
(2)初始化粒子群[1],粒子群規模N,確定每個粒子的位置xi和速度vi。
(3)設置目標函數,根據式(1)計算得出每個粒子的適應度值fi。
(1)
(4)比較每個隨機粒子的適應度值fi,取較小值。
(5)根據式(2)更新粒子的位置xi和速度vi。
(2)
式中,c1和c2為學習因子;ω為慣量因子;r1和r2為[0,1]范圍內的均勻隨機數。
(6)如果滿足結束條件就退出運行,否則返回(3)。
1.3 仿真運行
表1 仿真參數表

參數取值種群粒子數量N50學習因子c1、c21.494[2]參數取值慣量因子ω0.729[2]最大迭代次數M200
收斂曲線變化趨勢如圖2所示。大約迭代50次時,最小路徑長度基本穩定在41個單位;AGV運動軌跡如圖3所示。AGV在通往目標點的過程中,盡量選取了較短路徑,而且避開了所有障礙物。
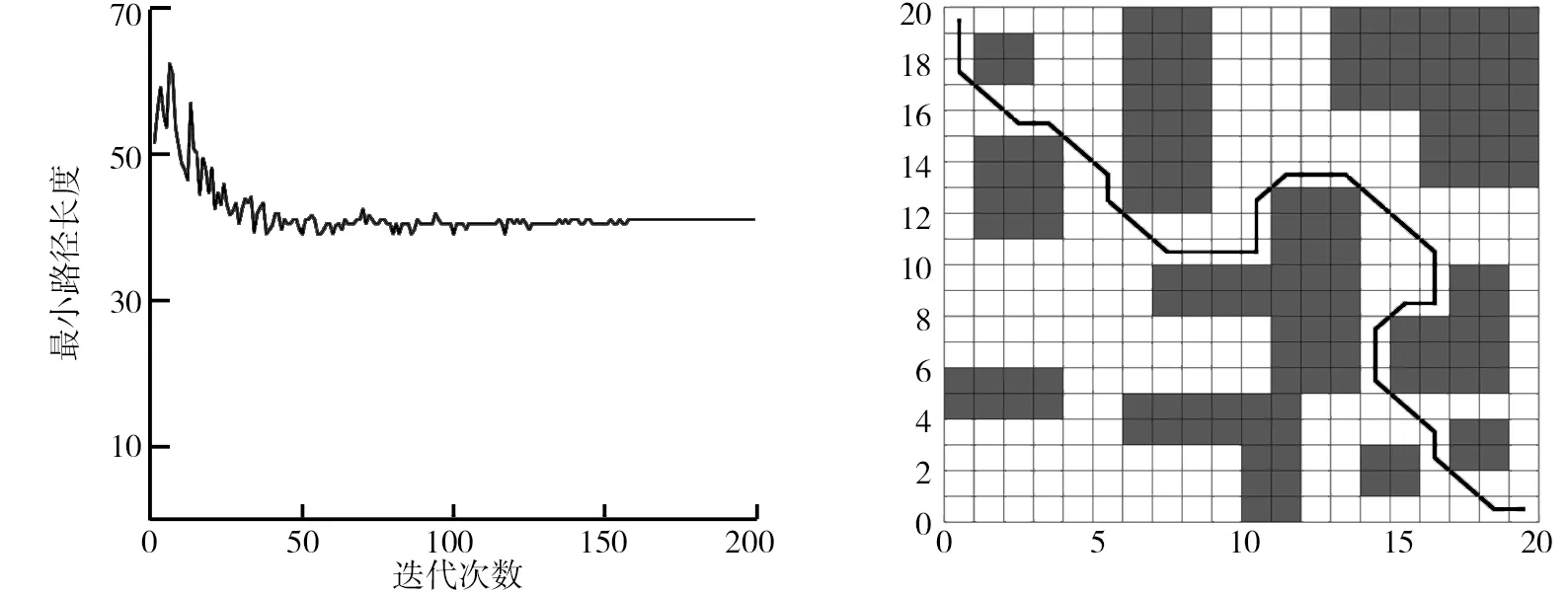
圖2 收斂曲線變化趨勢 圖3 AGV運動軌跡
2 數學建模
2.1 建立AGV的超聲波定位模型
在AGV中安裝超聲波傳感器[8],使AGV能夠利用回聲定位的方法來判斷障礙物的位置,進而將信息傳給中央控制器,從而做出避障行為。同時考慮到運行效果,模型采用3個超聲波測距模塊來改進控制效果,分別放在AGV的左側、前方、右側3個方向。
AGV在運行過程中,依靠發射和接收信號的時間差估計障礙物的位置,即回聲定位。AGV中的超聲波信號具有一定的指向性,利用兩個超聲波接收器接收信號,使其具有方位分辨能力,方位估計精度取決于兩個超聲波接收器的距離。
中遠場的二元測向模型如圖4所示。根據中遠場的二元測向模型,利用式(3)估計目標的方位角θ,即:
(3)
近場時的三元測向模型如圖5所示。根據近場時的三元測向模型,可以求出目標的聲信號到達各個陣元的時間差(c表示聲速):
(4)
(5)
(6)
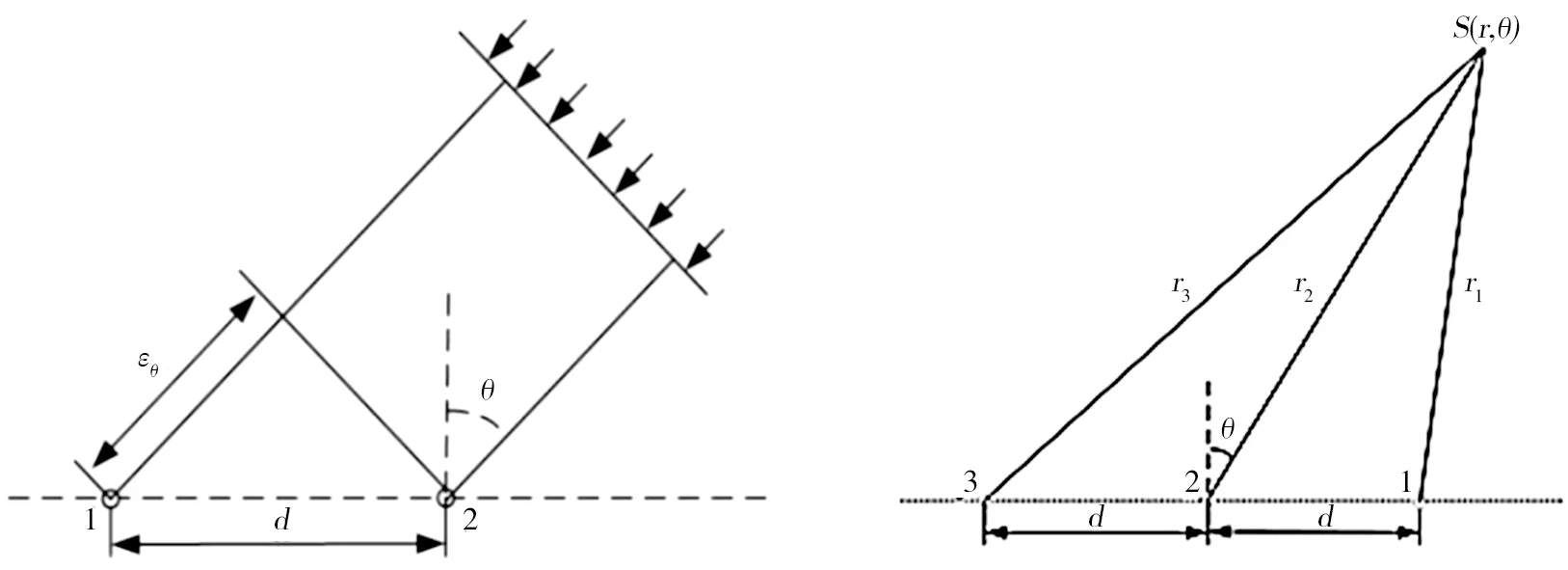
圖4 中遠場的二元測向模型 圖5 近場時的三元測向模型
聯立式(4)、式(5)、式(6)可推導出目標方位式(7):
(7)
通過模型分析可知,距離較遠時,根據二元測向模型,AGV的超聲波回聲定位只能判斷障礙物的方位,定位效果較差;距離較近時,根據三元測向模型,AGV的超聲波回聲定位能較精確地定位到障礙物的位置。
2.2 建立AGV運動模型
通過AGV的超聲波回聲定位模型,使得AGV自身擁有了一定的感知范圍。在感知范圍內,根據感知距離的大小將AGV的感知范圍設定為兩個區域,分別是:①當AGV和障礙物之間的距離到達一個臨界值,為防止相撞,AGV會改變運動軌跡,該區域稱為排斥區域Ⅰ;②當AGV與障礙物距離過遠,超過其感知范圍,則此時AGV和障礙物之間無任何聯系,該區域稱為無用區域Ⅱ。
在平面坐標系中,將AGV看做一個具有平面坐標和運動方向的矢量點。初始時刻t=0,設置AGV的運動速度且大小不變(AGV載重時所需速度不需要太大,近似認為作曲線運動與直線運動時速度大小相等),初始運動方向隨機給定。
針對運行中的AGV,設置了三大運動規則:(1)慣性運動規則。運動物體具有維持先前運動狀態的趨勢。因此AGV具有慣性運動。
AGV的初始單位慣性運動矢量為:
(8)
式中,(x0,y0)為AGV在t=0時刻隨機給定的初始慣性運動矢量。
(2)排斥運動規則。在排斥區域Ⅰ內,由于AGV在t時刻與障礙物距離過近,為了避免碰撞,AGV與障礙物之間會產生一種“排斥力”,從而改變AGV當前行進的運動方向:
(9)
式中,(mt,nt)為障礙物的平面坐標。
(3)吸引運動規則。在整體路徑規劃中,AGV會被預先設置目標點,由此目標點與AGV之間會產生一種“吸引力”,運行期間所有行為均是為了能夠無碰撞且快速地到達目標點:
(10)
式中,(xMM,yMM)為設置目標點的平面坐標。

圖6 AGV的運動規則
AGV的運動規則如圖6所示。取3個運動規則下的運動方向的合方向為AGV在t時刻的運動方向,表示為:
(11)
式中,M0為AGV初始慣性運動方向;Mt為AGV在t時刻的運動方向。
但是考慮到各個運動規則對AGV的影響效果不同,各規則對AGV進行運動決策的影響程度應通過層次分析法進行分析求解。故對公式進行改進,加入3個運動規則的貢獻度,則AGV在t時刻的運動方向為:
(12)
式中,λ1為慣性運動的貢獻度;λ2為排斥運動的貢獻度;λ3為吸引運動的貢獻度;且λ1+λ2+λ3=1。
AGV在t時刻的平面坐標為:
(13)
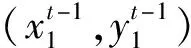
2.3 建立動態障礙物運動曲線擬合模型
考慮到動態障礙物運動方向和速度的隨機性,采用加權最小方差(WLS)擬合原理[9]來擬合動態障礙物的運動曲線。通過超聲波傳感器實時監測動態障礙物的位置信息,然后利用加權最小方差擬合原理進行數據分析,最后得到其運動曲線,這種數據擬合方法得到的曲線更加平滑且貼合運動規律。對應N階多項式的擬合公式,所需要求解的擬合系數需要求解線性方程組,其中線性方程組的系數矩陣和需要求解的擬合系數矩陣分別為:
(14)
使用加權最小方差法求解得到擬合系數為:
(15)
其對應的加權最小方差表達式為:
Jm=[Aθ-y]TW[Aθ-y]。
(16)
利用Matlab進行隨機數據的曲線擬合,通過調用rand()函數來實現基礎數據的隨機性。
研究分別設置比較1個與3個動態障礙物,均隨機取10個隨機數據進行曲線擬合,得到擬合曲線如圖7所示。即使遇到多個動態障礙物,該模型仍能很好地擬合各自的運動曲線。
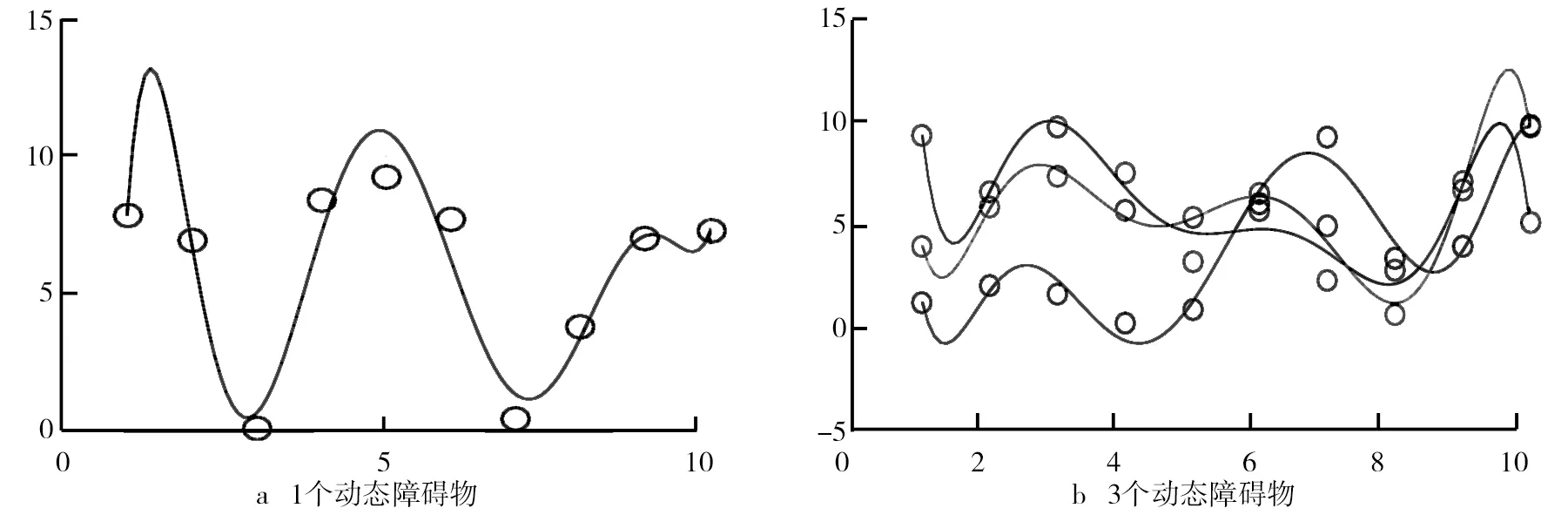
圖7 動態障礙物運動擬合曲線
3 動態環境的路徑規劃
3.1 模型分析
引入逐步判別法來實現動態避障控制。簡化AGV為一個質點,定義圓為不確定域[10],即動態障礙物在下一時刻可能出現的任意位置,其半徑為動態障礙物的最大步長。
假設AGV在通往目標點的可運行區域中(AGV此刻離動態障礙物較遠),在n次不同時刻對動態障礙物的位置進行了n次監測[11]。
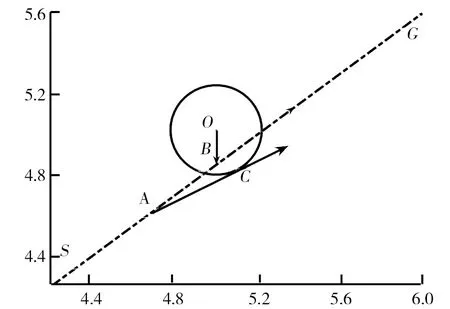
圖8 逐步判別法避障
逐步判別法避障如圖8所示。選取第n次監測,此時AGV在A點,O點位置為動態障礙物。下一時刻,按原定路線,AGV應到達B點。然而,B點在圓O的不確定域內,那么AGV在運行過程中存在一定概率與障礙物相撞,所以實際運行時AGV應偏轉一定的角度θ,才能繼續前進(如圖8所示,θ=∠BAC,為AB與圓O切線AC的夾角)。
若B點在圓O的不確定域外,則AGV按原定路線運行。重復以上步驟,直到AGV安全繞過所有障礙物到達目標點。
3.2 仿真運行
通過仿真分析,得到單個障礙物的運動擬合曲線和AGV的路徑規劃曲線。多隨機避障曲線如圖9所示。由圖9a可知,在自由柵格區域,AGV通過監測數據進行曲線擬合,判斷動態障礙物下一時刻可能出現的位置,進而有效地繞過了動態障礙物。由圖9b可知,再增加一個動態障礙物,仍然能夠完成基礎避障工作,驗證了該方案的可行性。
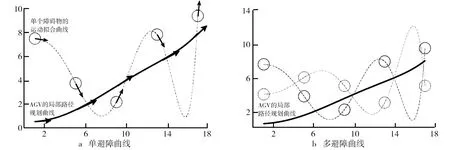
圖9 多隨機避障曲線
研究的方案對比文獻[7]的方案。其中,文獻[7]動態障礙物避障過程如圖10所示。文獻[7]的方案是對勻變速物體進行避障規劃的,而研究的方案可以規劃非勻變速的物體,并且具有較好的避障效果。
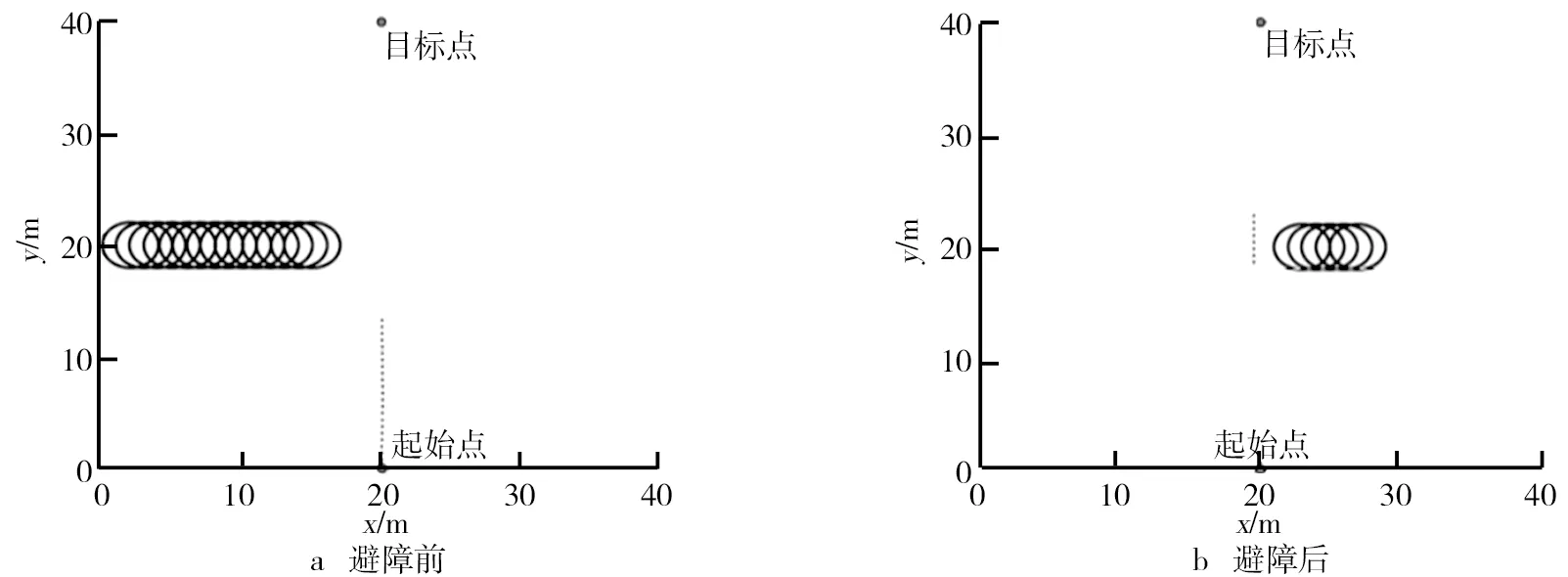
圖10 文獻[7]動態障礙物避障過程
4 結論
研究從靜態和動態兩個方面對AGV的最優路徑及避障控制進行分析:針對靜態環境,基于粒子群算法,通過柵格地圖簡化環境,得到AGV最短路徑的收斂曲線和運動軌跡,驗證了靜態環境規劃的有效性。針對動態環境,利用傳感器,建立AGV的超聲波定位模型和運動模型,推導出障礙物和AGV的位置信息,并通過加權最小方差原理擬合運動曲線,最后引入逐步判別法來實現動態避障控制。通過仿真分析,得到AGV多隨機障礙物的避障曲線,驗證了動態環境規劃的可行性。

