鐵的自旋轉變對菱鎂礦熱力學性質的影響

馬超杰，吳 瀟，馬陽陽，何開華，姬廣富

（1.中國地質大學（武漢）數學與物理學院，湖北 武漢 430074；2.中國工程物理研究院流體物理研究所沖擊波物理與爆轟物理重點實驗室，四川 綿陽 621999）

含碳固溶體的存在會影響地球內部的物理和化學性質[1-4]。近年來，菱鎂礦（MgCO3）被認為是碳進入地球深部的主要載體之一，因其在地球深部碳循環中的關鍵作用而引起廣泛關注[5-13]。Isshiki等[14]、Oganov等[15]的研究表明，菱鎂礦在下地幔的溫壓條件下能夠穩定存在；Hazen等[13]、Oganov等[15]開展的高溫高壓實驗研究揭示，菱鎂礦和菱鐵礦的固溶體[(Mg,Fe)CO3]可以在低于100 GPa的壓力條件下穩定存在。

鐵是多價態的過渡金屬，會對菱鎂礦和菱鐵礦固溶體的性質產生非常重要的影響。此外，鐵的自旋在一定的壓力和溫度條件下可以發生轉變，引起物理性質變化[16]。國內外學者對鐵方鎂石(Mg,Fe)O的自旋轉變開展了大量研究，結果表明，鐵方鎂石中的鐵（Fe2+）在40～50 GPa范圍內會從高自旋（High spin, HS）態向低自旋（Low spin, LS）態轉變，并伴隨著結構、電子、光學、彈性和熱力學性質的異常變化[16-28]。對于含鐵的菱鎂礦，已有的高壓穆斯堡爾光譜[29]、X射線發射光譜[30]、激光拉曼光譜[10]、X射線衍射[5,8,11]等實驗研究和第一性原理計算研究[31-32]都證實，(Mg,Fe)CO3中的鐵在約45 GPa時從HS態向LS態轉變，導致(Mg,Fe)CO3的體積比MgCO3減小6%～10%[11]。Liu等[11]、Hsu等[32]、Fu等[33]利用理論計算和實驗相結合的方法，詳細討論了彈性和地震波速在自旋轉變時的變化，得到了非常有意義的結果。其他熱力學參數如熱膨脹系數、格臨愛森常數和比熱容等在自旋轉變條件下的性質尚缺少報道。

本研究利用第一性原理計算方法，開展高溫高壓下(Mg,Fe)CO3在HS、LS及HS和LS態共存時的混合自旋（Mixed spin, MS）態的熱力學性質（熱膨脹系數、體變模量、體積、速度等熱力學參數）研究，并與不含鐵的MgCO3的相關性質進行對比，分析引起(Mg,Fe)CO3熱力學性質變化的機制。研究結果可為研究地幔深部碳的行為以及地幔在全球碳循環中的作用提供制約因素。

1 研究方法與理論

1.1 含鐵菱鎂礦的結構和計算參數

菱鎂礦MgCO3屬于三角晶系，其空間群為，原胞中包含10個原子（2個Mg原子、2個C原子和6個O原子）。為了討論鐵及其在高溫高壓下的自旋轉變對菱鎂礦物理性質的影響，本研究選擇用1個Fe原子替換1個Mg原子，得到Fe和Mg的摩爾比為1∶1，分子式為（Mg0.5Fe0.5）CO3。

幾何結構優化和相關能量的計算[34]采用基于密度泛函理論（Density of functional theory, DFT）的第一性原理分子動力學計算軟件VASP完成。由于結構中有鐵存在，需要考慮強關聯作用，因此計算中考慮了Hubbard參數U的影響，即LDA+U。已有的研究表明，U值會隨自旋轉變而改變，本研究選取Tsuchiya等[18]、Krukau等[35]通過線性響應理論計算得到的U值，分別為ULS= 5.3 eV，UHS= 4.0 eV。K點采用Monkhorst-Pack方法生成以Γ點為中心的15 × 15 × 15網格，截斷能設置為1 000 eV[36]。總能量的收斂閾值設置為1 × 10?6eV/cell，原子力的收斂閾值為1 × 10?3eV/cell。采用基于準諧近似的PHONOPY軟件計算得到二階原子間力常數（IFCs）、聲子譜和其他熱力學參數[37]。構造求解高對稱q點聲子頻率本征值的動力學矩陣，然后利用倒空間中動力學矩陣的傅里葉變換，計算其他一般q點的聲子頻率。所有計算中，以Γ為中心的q點網格選取為30 × 30 × 30。計算熱力學參數之前，用VASP軟件完成不同位移或不同體積下結構的能量計算，計算過程中的參數設置與上述幾何優化參數設置相同。

1.2 MS態熱力學參數

根據已有的研究結果，MS態時的吉布斯自由能可表示為

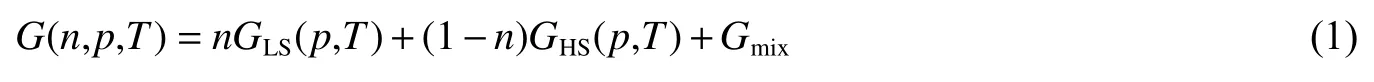
式中：n為LS態在MS態中所占的百分比，p為壓力，T為溫度，GHS、GLS分別為HS態和LS態的吉布斯自由能，Gmix為HS-LS混合態的吉布斯自由能。Gmix可以表示為

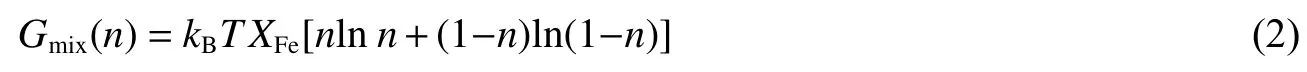
式中：XFe為鐵在含鐵菱鎂礦中的摩爾分數，kB為玻爾茲曼常數。在給定的壓力和溫度條件下，通過求最小化MS態吉布斯自由能得到LS態的占比n

式中：ΔGLS?HS為(Mg0.5Fe0.5)CO3在LS態和HS態的吉布斯自由能之差。對于Fe2+來說，自旋和軌道簡并量子數分別為s= 2，m= 3。得到n后可以推導出MS態的熱膨脹系數α(n)和等溫體積模量KT(n)分別為

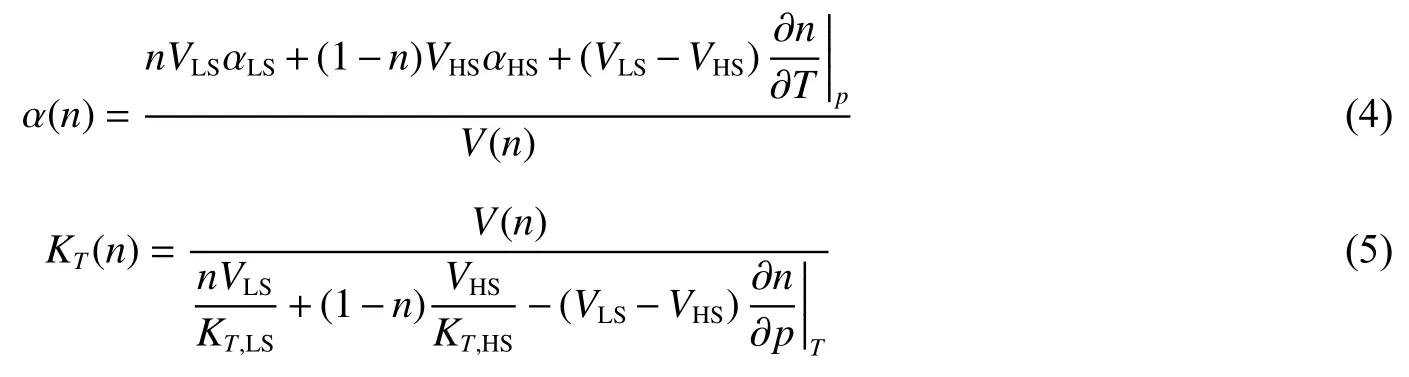
式中：KS為絕熱體積模量，CV,m為定容比熱容，ρ為密度。根據上述公式可以計算出MS態下的體積V、速度v和格臨愛森常數γ。

2 結果與討論

2.1 Fe2+的自旋轉變

含鐵菱鎂礦(Mg0.5Fe0.5)CO3的LS態與HS態的焓差ΔH（HHS-HLS）隨壓力的變化趨勢如圖1所示。由圖1可知：在低壓時，ΔH＜ 0，HS態的焓值小，因此 HS 態更穩定；在高壓時，ΔH＞ 0，LS 態的焓值變小，LS態變得更穩定。本研究計算得到的自旋轉變壓力為44.5 GPa，與實驗觀察得到的結果（40～52 GPa）很好地符合[5,10-11,29-30]，與 Hsu 等[32]的計算結果（48 GPa）也符合較好，較小的差異源于鐵在含鐵菱鎂礦中的摩爾分數不同。

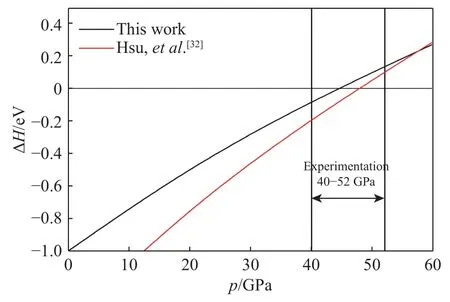
圖1 (Mg0.5Fe0.5)CO3的LS態與HS態的焓差ΔH（HHS-HLS）隨壓力的變化Fig.1 Pressure dependence of the enthalpy difference (ΔH)between LS state and HS state (HHS-HLS） for (Mg0.5Fe0.5)CO3

2.2 含鐵菱鎂礦HS態與LS態的熱力學性質

圖2(a)給出了菱鎂礦含鐵前后的體積對比。由圖2(a)可以看出，菱鎂礦含鐵后HS態對應的體積比LS態對應的體積大，在30 GPa、300 K的溫壓條件下，(Mg0.5Fe0.5)CO3在HS和LS態下的體積分別為77.138 10 ?3和73.366 07 ?3，自旋轉變后體積減小5.0%左右。對比含鐵菱鎂礦與不含鐵菱鎂礦的體積可知，含鐵菱鎂礦LS態的體積減小，HS態的體積則在低溫端增大，在高溫端減小，說明含鐵菱鎂礦的HS態對應的熱膨脹系數小于不含鐵菱鎂礦。本研究中自旋轉變導致的體積變化幅度比Liu等[11]實驗測量得到的變化幅度稍小，這是由于實驗所用樣品為(Mg0.35Fe0.65)CO3，體積變化幅度的差異源于測量樣品中鐵的摩爾分數不同。

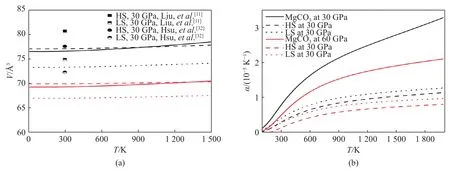
圖2 (Mg0.5Fe0.5)CO3的HS態與LS態的體積V（a）和熱膨脹系數α（b）隨溫度的變化關系Fig.2 Temperature dependence of the (a) volume V, (b) thermal expansion coefficient α for both the HS and LS state of (Mg0.5Fe0.5)CO3

熱膨脹系數是研究礦物熱力學性質的重要參數，本研究計算了含鐵對菱鎂礦熱膨脹系數的影響。圖2(b)分別給出了含鐵菱鎂礦的HS、LS態在30 GPa和60 GPa時的熱膨脹系數，為了便于比較，圖2(b)中給出了對應壓力下MgCO3的熱膨脹系數以及部分前人的結果[11,32]。由圖2(b)可知，在相同的溫壓條件下，(Mg0.5Fe0.5)CO3的HS與LS兩種自旋態的熱膨脹系數均小于MgCO3，即含鐵會導致菱鎂礦的熱膨脹系數急劇減小。在30 GPa、300 K的溫壓條件下，計算得到MgCO3與(Mg0.5Fe0.5)CO3的熱膨脹系數分別為 8.05 × 10?6K?1和 3.13 × 10?6K?1，減小幅度為 61.0%；(Mg0.5Fe0.5)CO3的 HS 和 LS 態的熱膨脹系數分別為 3.13 × 10?6K?1和 4.22 × 10?6K?1，鐵的自旋轉變導致的熱膨脹系數增加幅度為 34.8%。此外，熱膨脹系數會隨著壓力的增加而減小，并且對溫度的依賴性減弱。這與含鐵方鎂石在低壓下HS態的熱膨脹系數比LS態大，而在高壓下HS態的熱膨脹系數反而比LS態小的變化趨勢有所差別[28]。根據格臨愛森定律

由于影響熱膨脹系數的主要物理量為格臨愛森常數γ、定容比熱容CV,m、體積模量ΚT及體積V，因此可以從上述熱力學參數的變化來解釋含鐵菱鎂礦熱膨脹系數的變化機制。

圖3給出了(Mg0.5Fe0.5)CO3的熱力學參數隨溫度和壓力的變化關系。由圖3可知，定容比熱容在低溫段先隨溫度升高而急劇增大，隨后趨于飽和，MgCO3的定容比熱容為 231.75 J/(mol·K)，(Mg0.5Fe0.5)CO3在HS、LS態時的定容比熱容分別為 232.99 J/(mol·K)和 231.58 J/(mol·K)，彼此之間的差異很小，因此定容比熱容對熱膨脹系數的影響可以忽略不計。由1.2節的研究結果可知，菱鎂礦含鐵及鐵的自旋轉變引起的體積變化在5.0%左右，無法成為熱膨脹系數劇烈變化的決定性因素。由圖3(b)和圖3(c)可知，菱鎂礦含鐵后格臨愛森常數明顯減小，由HS態轉變為LS態后明顯增大，與熱膨脹系數的變化趨勢很好地符合。需要注意的是，含鐵菱鎂礦LS態的格臨愛森常數γ比不含鐵時大，而熱膨脹系數卻比不含鐵時小，由此可以推斷，體變模量KT對熱膨脹系數的變化也起到至關重要的作用。因此，菱鎂礦含鐵及鐵的自旋轉變導致的熱膨脹系數變化是由格臨愛森常數γ與體變模量KT共同決定的。

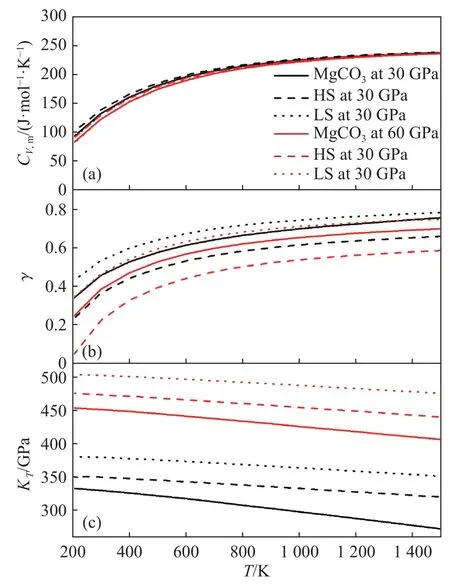
圖3 MgCO3與（Mg0.5Fe0.5）CO3的定容比熱容CV,m(a)、格臨愛森常數γ(b)、體變模量KT(c)與溫度的關系Fig.3 Temperature dependence of the (a) specific heat capacity of constant volume CV,m, (b) Grüneisen parameter γ,(c) bulk modulus KT of MgCO3 and (Mg0.5Fe0.5)CO3

2.3 含鐵菱鎂礦MS態的熱力學性質

Liu 等[11]、Hsu 等[32]、Fu 等[33]的研究表明，含鐵菱鎂礦的MS態在高溫高壓下會引起彈性及聲速的異常變化。研究MS態熱力學參數的前提是計算出自旋共存時LS態的占比n。根據式（1）～式（8）計算出MS態下LS的占比n，n對p和T的一階導數以及α、V、v等熱力學參數。

圖4給出了不同溫度下n隨壓力的變化關系。由圖4可知：在低溫時，n急劇增大到1，即HS態與LS態共存的壓力區間很窄；隨著溫度升高，HS態與LS態共存的壓力區間明顯增大；當溫度為300 K時，HS態與LS態共存的壓力區間約為5 GPa；溫度為1 500 K時，兩者共存的壓力區間增大到約15 GPa，與Liu等[11]、Hsu等[32]通過實驗和理論計算得到的趨勢一致。同時，通過計算發現：自旋轉變的壓力隨溫度的升高而增加；溫度為300 K時，自旋轉變發生在約40 GPa；而溫度為3 000 K時，自旋轉變發生在約60 GPa。該自旋轉變行為在鐵方鎂石的理論計算和實驗研究中也有報道[18,20,22,38-40]。HS態與LS態共存區間和自旋轉變隨壓力的變化關系決定了n對溫度和壓力的一階導數，如圖5所示。計算表明：當壓力為50 GPa時異常變化的起始溫度為500 K左右；70 GPa時異常變化的起始溫度為1 500 K左右。同時峰的寬度也由50 GPa時的1 000 K增大到70 GPa時的1 700 K，由此可知，自旋轉變引起的峰隨著壓強的增加向高溫方向移動，同時峰的寬度也隨之增加。圖5(b)給出了隨壓強的變化關系，其峰高和峰寬隨壓力的變化趨勢與類似。

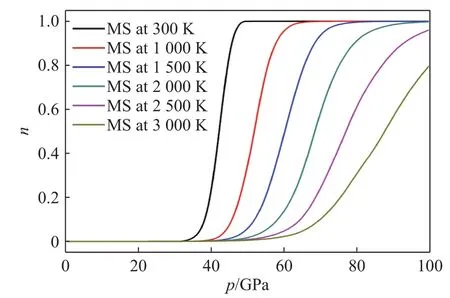
圖4 n隨溫度和壓力的變化關系Fig.4 Ratio n as the function of pressure at different temperature

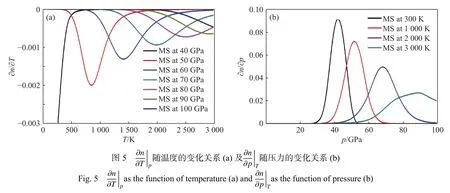
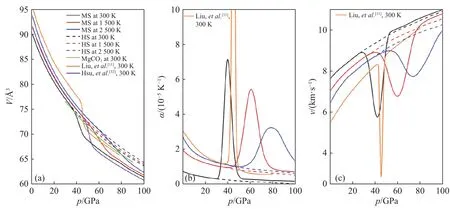
圖6 MS態的體積V(a)、熱膨脹系數α(b)、速度v(c)隨壓力的變化關系Fig.6 Volume V (a), thermal expansion coefficient α (b), velocity v (c) of MS state as the function of pressure

圖6(b)和圖6(c)分別給出了熱膨脹系數α和速度v隨壓力的變化關系。由MS態時熱膨脹系數的計算公式(4)可知，α主要受到LS態的占比n對溫度的一階導數的影響，其中α與成反比，由圖5(a)可知，隨著HS態向LS態發生自旋轉變，在自旋共存區間內的變化趨勢為先突然減小然后增大，因此熱膨脹系數α的變化趨勢為先突然增大然后減小，這與體積的變化趨勢不同；由式（5）、式（6）、式（8）可知，MS態的速度主要由LS態的占比n對壓強的一階導數決定，且v與成反比，由圖5(b)可知，在自旋共存區間內，的變化趨勢為先突然增大后減小，因此速度v在自旋共存區間的變化趨勢為先突然減小然后增大。在300 K時，MS態(Mg0.5Fe0.5)CO3在約40 GPa時產生異常變化，而在1 500 K時，這類異常變化出現在約50 GPa，該變化趨勢與的變化一致，表明熱力學參數的變化受n的影響。α、V、v由于自旋轉變引起的異常隨溫度的增大向高壓方向移動，并且變得更加平滑，但在2 500 K左右時，α、V、v的異常仍然比較明顯。本研究計算結果與前人的實驗研究均符合較好，在相同溫度下，僅峰的位置存在較小的偏差，這是由于實驗中Fe2+的濃度較高，其自旋轉變的壓力也隨之相應地提高。(Mg0.5Fe0.5)CO3的MS態體積和速度的異常變化也會影響其在地球深部條件下的熱傳導特征。

3 結 論

采用第一性原理計算方法研究了含鐵菱鎂礦(Mg0.5Fe0.5)CO3中鐵的摻入以及自旋轉變對其熱力學性質的影響，得出以下主要結論。

（1）含鐵后菱鎂礦晶體的體積發生明顯變化，HS態在低溫端體積增大，而在高溫端體積比不含鐵時減小，LS態的體積明顯減小，表明鐵的自旋轉變會導致含鐵菱鎂礦晶體體積減小。

（2）含鐵后菱鎂礦的熱膨脹系數顯著減小，但是鐵的自旋轉變導致熱膨脹系數有所增大，但仍然比不含鐵時要小；格臨愛森常數與體變模量的變化是熱膨脹系數變化的主要決定因素。

若要進一步明確含鐵菱鎂礦的熱力學性質對地幔在碳循環中的作用，還需全面考慮地幔中其他礦物對菱鎂礦的影響，如鐵方鎂石和鈣鈦礦等在地球深部同時存在時所表現出的物理化學性質。