注重深度體驗，打造高效課堂
——從一次“一課三上”研討說起

江蘇省蘇州工業園區斜塘學校 郭建芬

《不含括號的三步混合運算》是蘇教版四年級上冊的內容，是在學生已經理解了四則運算的意義，掌握了兩步混合運算順序的基礎上進一步學習的。 “如何基于兒童，打造高效課堂”是教學的永恒追求，數學教研組三位青年教師圍繞這課進行一次“一課三上”專題研討活動，結合實踐提出了一些思考。

【首次教學】——按部就班，學生“被學習”

本課教學立足書本，依托書本例題和習題主要圍繞四個環節進行教學：復習回顧、引入新課；聯系實際，探究新知；練習鞏固、強化認知；全課總結，交流收獲。在數學課堂教學中，比較是常見的數學思想方法之一，也是促進學生思維發展的手段。因此，在課的新授部分和“試一試”，教師都注重引導學生對比，并掌握相應的混合運算的運算順序，學會正確計算。第一次執教，教師有條不紊地展開教學，總體感覺課上得比較流暢，學生配合度較高。但是縱觀全課不難發現課堂上教師過于“包辦”，“一問一答”的教學模式導致學生“被學習”，學生的主體意識沒有被真正喚醒，主動性沒有被真正發揮，思維沒有被真正激活。如何讓學生更自主、更高效地學，教研組再次研讀課標、分析學情，重新定位，進行了第二次跟蹤教學。

【跟蹤教學】——嘗試翻轉，難點“難突破”

【片段一】課前預學，交流反饋

師：這節課我們一起探究的課題是《不含括號的三步混合運算》，同學們課前已經通過微課、導學單進行了自主預習，通過預習你有什么收獲嗎？

生1：在沒有括號的算式里，先算乘除，再算加減。

生2：只有乘、除的部分，還是按照順序計算。

師：你預習得很認真！那大家有什么疑惑嗎？

師：其實三步混合運算中還有一些非常值得探討的問題，希望這節課我們能有更大的收獲！

【片段二】新知探究，質疑釋疑

1.例題再現

師：從圖中你獲得什么信息？

生：有3 副中國象棋，每副12 元，4 副圍棋，每副15 元，問題是一共要付多少元。

師：一共要付多少元，你是怎樣想的？

生：3 副中國象棋的錢加上4 副圍棋的錢。

師：可以怎樣列綜合算式？

生：12×3+15×4。

師：老師搜集了同學們的例題解答過程，有兩種，這兩個算式各是按怎樣的運算順序計算的？你能對照例題圖說一說嗎？

課件出示

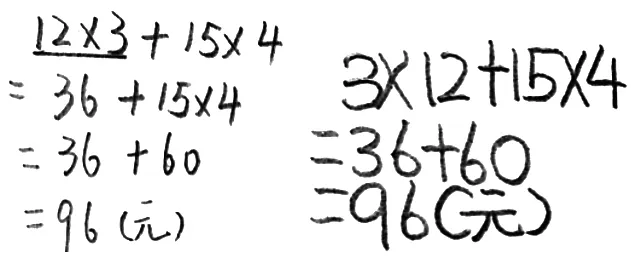
生：第一種先算12×3，3 副中國象棋的價錢，再算15×4，4 副圍棋的價錢；第二種同時計算12×3，15×4。

師：你更喜歡哪一種？為什么？

生：更喜歡第一種，過程比較簡便。

師：像這樣的，兩邊是乘法，中間是加法的算式，可以先同時計算兩邊的乘法，再計算中間的加法，這樣更簡便，數學就是要講究簡潔美。

2.變一變

師：你根據上面的4 個條件你還能提出什么問題？

生1：4 副圍棋比3 副中國象棋貴多少錢？

生2：4 副圍棋的價錢-3 副中國象棋的價錢=4 副圍棋比3 副中國象棋貴的價錢。

交流匯報，列式與計算過程

過渡：剛才我們解決的兩個算式，都是兩頭是乘法，中間是加或減，計算的時候先算兩頭的乘法，再算中間的加或減。

3.試一試

出示: 150+120÷6×5。

師：同學們仔細觀察一下這道算式， 它與前面的算式有什么相同或不同？

生1:相同之處都有3個運算符號，4 個數，不同的是，前面算式兩頭是乘、中間是加或減，這個算式前面是減，后面是除和乘。

生2：前面的兩個乘是分開的，這道算式的乘和除是連在一起的。

……

這次教學努力體現“先學后教，以學定教”的理念。教師課前引導學生觀看微課進行預學，設計導學單了解學生對新知的掌握情況，分析學生學習的難點，引領孩子經歷了課前“試學”—課中“探學”—課后“用學”的全過程，努力實現“為疑難而教，為發展而教”。但是縱觀全課學生課前預習后似懂非懂，有的學生預習只是停留在表面，對于如何正確計算三步混合運算認識還比較模糊，尤其是對于有乘除和加法或乘除和減法這類運算的運算順序出現混淆，書寫也欠規范，教師雖然能夠選擇預習過程的一些錯誤進行糾錯、化錯，但是因為學生的參與度不夠，生成性資源未能靈活運用，教學難點并沒有得到有效突破，作業正確率不容樂觀。于是再次調整，重點推敲針對新授和練習環節，進行了第三次跟蹤研討。

【再次跟蹤】——深度體驗，課堂顯“高效”

引入環節基本相同。重點在探索新知環節做了調整，以數量關系為抓手，以“問題引領”為契機，引領學生經歷獲取信息、提出問題、分析問題和解決問題的全過程，練習環節設計了說、玩、改等類型，通過對比題、游戲“順序大師”等，凸顯了三步混合運算的運算順序的價值。

【片段三】

課件出示例1 情景圖。

師：從圖中，你能獲取哪些數學信息？

生：小女孩買了3 副中國象棋和4 副圍棋；一副中國象棋12 元，一副圍棋15 元。

課件動態演示將這些條件標上序號① ② ③ ④。

師：那么哪些條件之間是有關聯的呢?

生：①和③， ②和④。

師：根據這些條件我們能夠解決哪些問題呢？

生1：買中國象棋用去多少錢？圍棋用去多少錢？

生2：買一副圍棋比一副中國象棋多花多少元？（或買一副中國象棋比一副圍棋少花多少元？）

生3：買圍棋比買中國象棋多花多少元？（或買中國象棋比買圍棋少花多少元？）

生4：一共要用多少錢？

師：同學們真了不起，提出了這么多問題，那么這節課我們重點來研究“一共要付多少元”這個問題。怎么解決這個問題呢？

生：就是把3 副中國象棋的錢和4 副圍棋的錢相加。

出示數量關系式：一共要付的錢= 3 副中國象棋的錢+4 副圍棋的錢。

師：怎么列綜合算式呢？3 副中國象棋的錢可以用哪個算式代替？

生：12×3。

師：4 副圍棋的錢呢？

生：15×4。

師：最后不要忘記把它們相加。

觀察這個算式，里面有加法和乘法，我們應該先算什么呢？這里幾個“×”？

師：和加法相比，乘法屬于高級運算，所以這2 個“×”要同時計算。（課件出示畫線的過程）

【片段四】

1.說一說：先說出下列算式的運算順序，再完成計算。

37+12×3÷4 20+4×5-3

37+12÷3×4 20÷4×5-3

師：仔細觀察上下兩組算式，你有什么發現？

生：數字相同，運算符號不同。

師：運算符號不同會引起哪些變化？

生：運算順序變了，運算結果也變了。

2.玩一玩。

出示游戲規則：將你所看到算式的運算順序寫在橫線上。如：看到 2×4-4÷2，就寫 ×、÷、-。

課件依次快速閃過以下算式，學生在橫線上寫出運算順序。

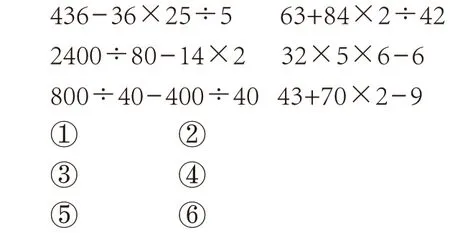
【反思展望】

一次教學一次反省一次進步，發現問題、剖析問題、跟進調整，每次都有新的突破。第一次立足教材，以本為本，帶著學生參與學習。第二次先學后教，以學定教，以學為本，努力實現教學方式的轉變，力求把主動權還給學生。第三次教學立足學生的認知起點，尋找新舊知識的生長點，抓住數量關系，問題引領，努力實現自主遷移，自主建構，深度體驗，打造高效課堂，促進學生思維的發展。

1.注重細節，問題引領，實現三維目標的和諧發展。

小學數學課堂教學應致力于讓學生積極參與、自主探究，學生不應該是知識的被動接受者，而應該是在學習的過程中主動積極的參與者，是認知過程的探究者，是學習活動的主體，通過學生自身的活動，對知識的理解更深刻，應用得更靈活，同時也培養了學生發現問題、分析問題、解決問題的能力。教學中，在處理新授時，教師注重條件的整理，問題的引領，關注數量關系，使學生明確每一步算式的意義，將算式的意義具體化，引導學生掌握基本的解決問題的思路，同時在解決的過程中明確運算順序，讓學生感悟到數學方法的價值，體會到學習的樂趣與成就感，實現三維目標的和諧發展。

2.同中求異，異中見同，實現教學難點的有效突破。

教師有意識地將例題和練習中的題目進行適度整合，形成對比，讓學生充分暴露問題，剖析問題，使得學生在練習中自主發現計算練習的易錯、易混點，自主辨析錯誤、糾正錯誤，讓學生認識到在有乘除和加減運算中不管是乘在前還是除在前，都要先乘除后算加減，同級運算一定要遵循從左往右的運算順序，完善了認知結構，掃清認知障礙，凸顯了知識的本質，有效突破了教學難點。

3.合理定位，實現習慣和技能的同生共長。

“不含括號的三步混合運算”既是發展學生計算能力的需要，又是學習運算律（含簡便運算），以及小數、分數混合運算的基礎，所以在小學數學運算教學中起到承上啟下的作用。教學時既要研讀教材，又要分析學情，合理把握學生的認知起點，提供給學生充分的探索空間，在抓實計算習慣的同時實現技能和習慣的同生共長。堅持“一看（運算符號）、二想（運算順序）、三做（正確計算）、四查（認真檢查）”，養成認真嚴謹、細致計算的學習習慣，樹立數學規則意識，提升數學素養。