多面體網格在滑行艇數值仿真計算中的應用

李昆鵬，魏成柱，梁曉鋒

(1. 陸軍研究院作戰保障研究所，江蘇 無錫 214035；2. 中國艦船研究設計中心上海分部，上海 201108；3. 上海交通大學 海洋智能裝備與系統教育部重點實驗室，海洋工程國家重點實驗室，上海 200240)

0 引 言

滑行艇在軍事和民用領域的應用非常廣泛，其相關研究工作也在大量進行。傳統上，滑行艇的設計和優化工作基于經驗公式和模型試驗。隨著CFD 技術的發展，模型試驗結合CFD 成為滑行艇設計優化和性能分析的主流手段之一。CFD 技術在滑行艇水動力性能分析中扮演了愈來愈重要的角色。相比潛艇和排水型船，高速滑行艇的數值仿真難度更大。Brizzolara等[1]和王碩等[2]分別進行了滑行艇數值仿真計算精度的研究，均使用了NACA 公布的滑行楔形體模型。Brizzolara 等在數值仿真計算中使用了六面體網格，王碩等在數值仿真計算中使用了六面體網格和切割體網格。他們的研究工作表明基于CFD 的滑行艇數值仿真精度很高，誤差在實驗測量誤差之內，表明基于CFD 的滑行艇數值仿真計算可以應用于實際工程中。

網格是CFD 分析的基礎。現實中的滑行艇通常具有復雜幾何形狀的船體表面，經典的六面體網格很難對其進行網格劃分。因此，采用非結構性網格成為解決此類網格貼面問題的重要手段。傳統上，四面體網格被用來適配一些滑行艇的復雜幾何表面，但近年來切割體網格（trimmed mesh 或cut cell）開始得到比較廣泛的應用。除了非結構性的四面體網格和切割體網格外，多面體網格也逐漸得到廣泛應用。多面體網格已經在空氣動力學相關領域有了廣泛的應用并贏得良好的口碑[3]。但是多面體網格在海洋工程領域中的應用十分有限。多面體網格是一種非結構網格。二維多面體網格主要由六邊形網格構成，其幾何形式廣泛存在于自然界中；三維多面體網格單元為任意多面體形狀。多面體網格在引入可靠的基于面的有限體積法和相關的多面體網格生成器后才逐漸可用，并在近幾年得到了商業解算器的推廣。相較于同為非結構網格的四面體網格，多面體網格有更多的臨近單元，能夠更加精確地計算梯度及局部的流動狀況，并且對幾何變形沒有四面體網格敏感。對于一種新興的并具有良好特性的網格，有必要驗證其在海洋工程領域中的適用性。

研究人員在對滑行艇進行數值計算時經常會遇到偽擴散的問題。 一層薄空氣層會附在船體，與實際船體表面水氣分布不符合。若使用VOF 法[4]捕捉自由面，偽擴散意味著船體浸沒表面部分或全部的水組分不等于1。這個空氣層會直接影響船體表面的切應力。偽擴散解方程歐拉型模式所特有的，其大小與所用的有限差分格式有關。為了克服偽擴散，須采取特殊的技術措施和各種不同的差分格式。在網格設置方面，克服偽擴散的方法有增加網格密度，沿流線方向布置網格。王志剛等[5]指出，網格加密10 倍偽擴散效應就減小1 個量級。每個方向按10 倍進行加密，那么3 個方向的網格數將是原網格數的1 000 倍，需要付出極大的計算代價。故采用網格加密不能有效減小偽擴散效應，而沿流線方向布置網格總體上僅對靜態仿真有效，當網格發生改變時原有優化布置的網格很可能不再與流線方向相符合。此外，FRISK[6]在研究中通過添加源匯，強制性將船體濕表面處水組分小于0.7 的地方設置為1。Spiegel 等[7]對比分析了四面體網格和多面體網格在腦血管動力學仿真計算中的應用效果，認為多面體網格收斂性更好，且對WSS（wall shear stress）的計算更準確，這對計算滑行艇的摩擦阻力是有益的。參考文獻[7]并考慮到多面體網格有更多的臨近單元，能夠更加精確地計算梯度及局部的流動狀況，本文嘗試通過使用多面體網格處理滑行艇數值仿真中遇到的偽發散問題。

研究證實，基于多面體網格滑行艇的水動力預報具有相當高的精度，完全滿足工程需要，多面體對控制滑行艇仿真計算中出現的偽擴散問題有很大改善。

1 多面體網格計算精度分析

使用NACA 公開的滑行楔形體幾何模型及相關的實驗設置和實驗數據[8]。滑行楔形體的幾何尺寸參見文獻[8]，幾何模型如圖1 所示。選擇底部斜升角為20°的模型。仿真計算采用固定模式，即模型初始狀態設置為水池實驗中測量到的狀態。選擇其中幾個典型的工況進行仿真計算，如表1 所示。實驗中測得的升力平均相對誤差為3%，最大相對誤差為8%；測得的阻力平均相對誤差為20%，最大相對誤差為50%；速度平均相對誤差為0.70%，最大相對誤差為1.30%；吃水平均相對誤差為5%，最大相對誤差為10%；縱傾角平均相對誤差為2%，最大相對誤差為5%。

圖 1 NACA 滑行楔形體幾何輪廓Fig. 1 NACA planing wedge

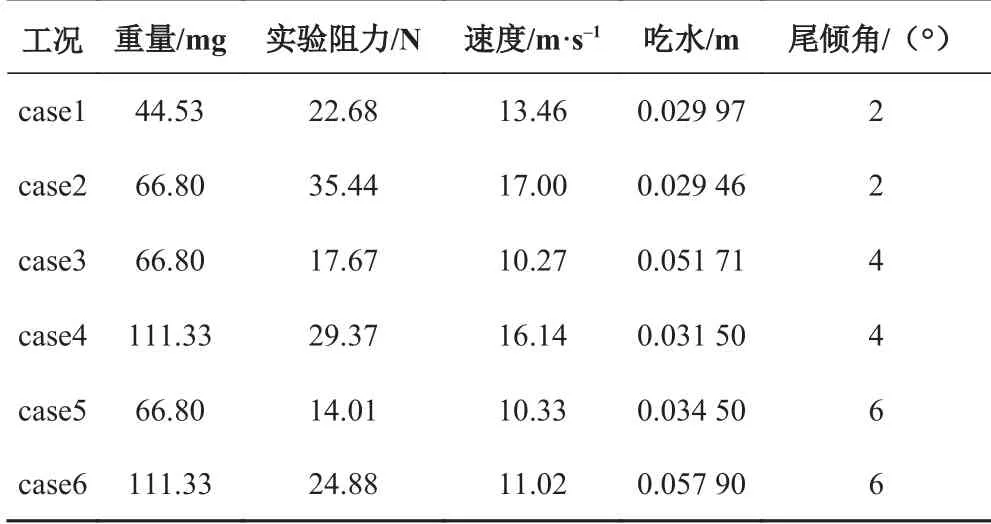
表 1 基于NACA 滑行楔形體的數值計算工況統計Tab. 1 Statistics on simulations of NACA planing wedge

數值仿真計算使用重疊網格，背景網格使用切割體網格控制網格密度，減小網格數量和提高網格的分層性和正交性。隨體網格通過合理布置獲得良好分層性和正交性的多面體網格。合理布置網格密度及改善網格的正交性和分層性對自由面鋸齒現象的消除及興波與飛濺的捕捉非常關鍵。計算域和網格設置如圖2所示。由于使用重疊網格，網格數量在260 萬左右。

計算選用STAR CCM 作為求解器來求解非穩態RANS方程。數值計算選用SST k-ω[9]湍流模型。為了對自由面的捕捉，使用VOF（volume of fluid）模型。為了減小計算代價并參考文獻[10]，使用高yplus（又稱y+）壁面函數和較為粗糙的近壁面網格在一定程度上減少網格數量來提高計算速度。

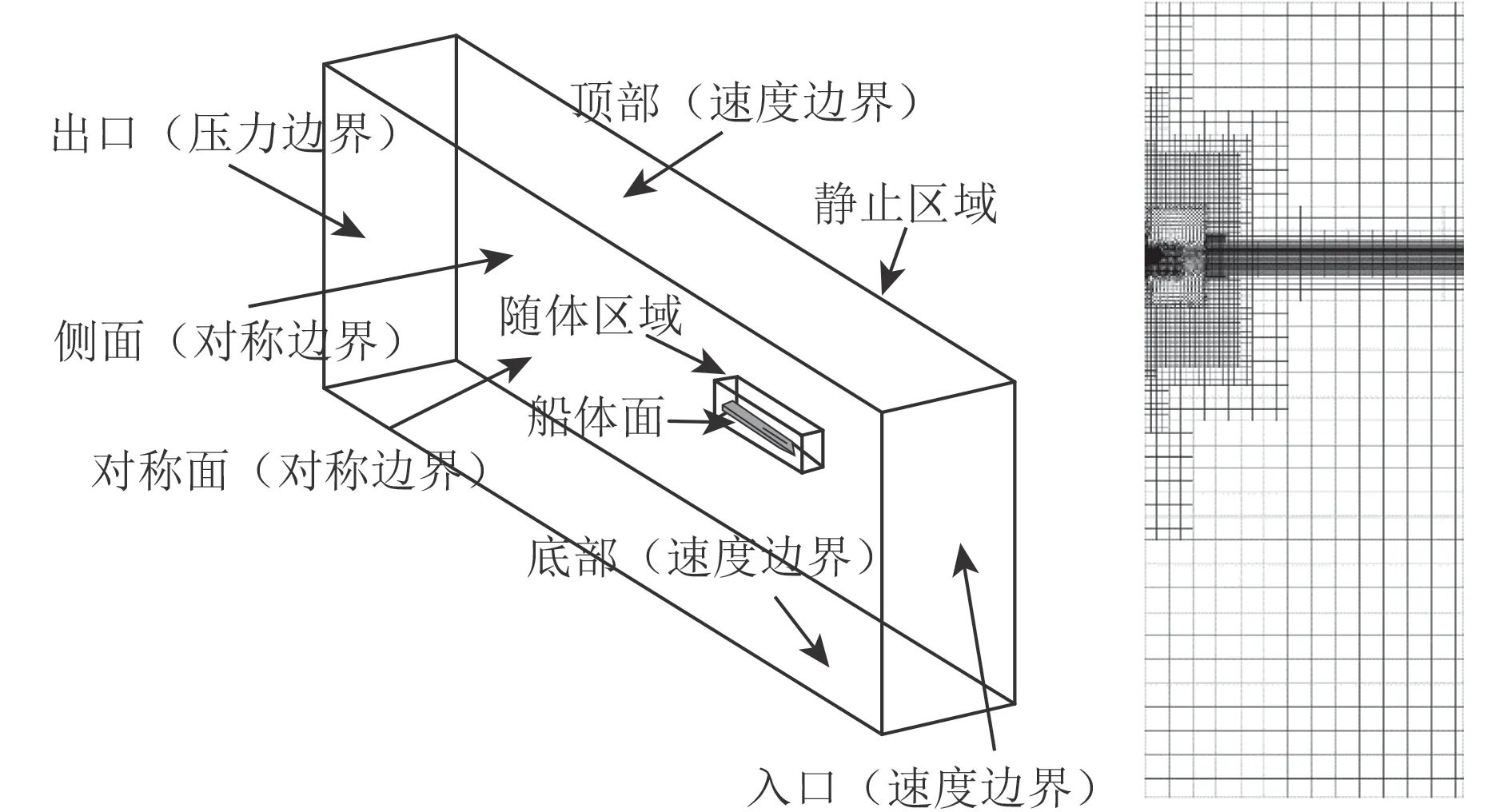
圖 2 基于NACA 滑行楔形體的計算域設置及網格Fig. 2 Computational domain settings and mesh

數值仿真計算給出了光順的興波圖，在傳統非結構網格在波形描繪中出現的等高線鋸齒現象有很大改善，如圖3 所示。將本文的計算結果同水池實驗結果及文獻[1] 和文獻[2] 中的阻力和升力結果進行匯總（見表2 和表3）。表4 和表5 進一步匯總了本文及文獻[1]和文獻[2]中的計算誤差。文獻[1]基于六面體網格的計算結果標記為HEX-1；基于六面體網格的計算結果標記為HEX-2，文獻[2]基于切割體網格的計算結果標記為TRIMMED；本文的計算結果標記為POLY。對比文獻[8]中NACA 給出的水池一般性固有誤差可見，基于多面體網格的數值仿真計算的升力誤差與其3%固有平均誤差相比稍微偏大，但誤差均小于最大相對誤差，而阻力計算誤差遠小于其20%的參考值。同其他計算結果對比表明，基于多面體網格的阻力預報的精度稍高，而升力的預報的誤差稍微偏大。對比每一個工況下不同網格的阻力和升力預報可知，基于多面體網格的預報結果誤差值和分布具有一定的相似性。

通過以上對比可見，基于多面體網格的滑行艇水動力預報具有相當高的精度，完全滿足工程需要。

2 多面體網格對偽擴散的改善

圖 3 NACA 滑行楔形體興波（case2）Fig. 3 Wave making of NACA planing wedge (case2)

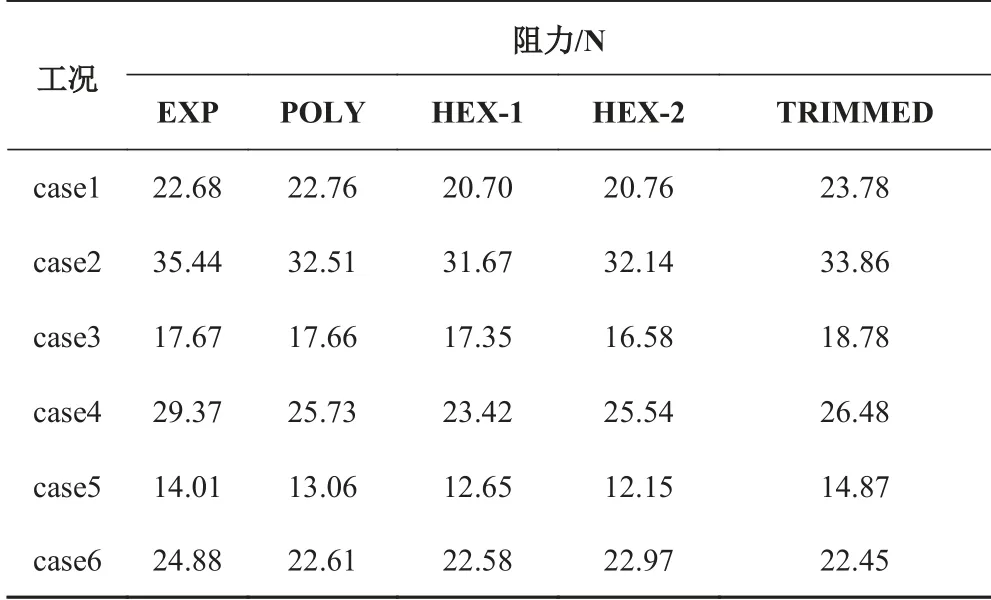
表 2 不同網格的NACA 滑行楔形體阻力計算結果Tab. 2 Numerical results of drag of NACA planing wedge based on different meshes

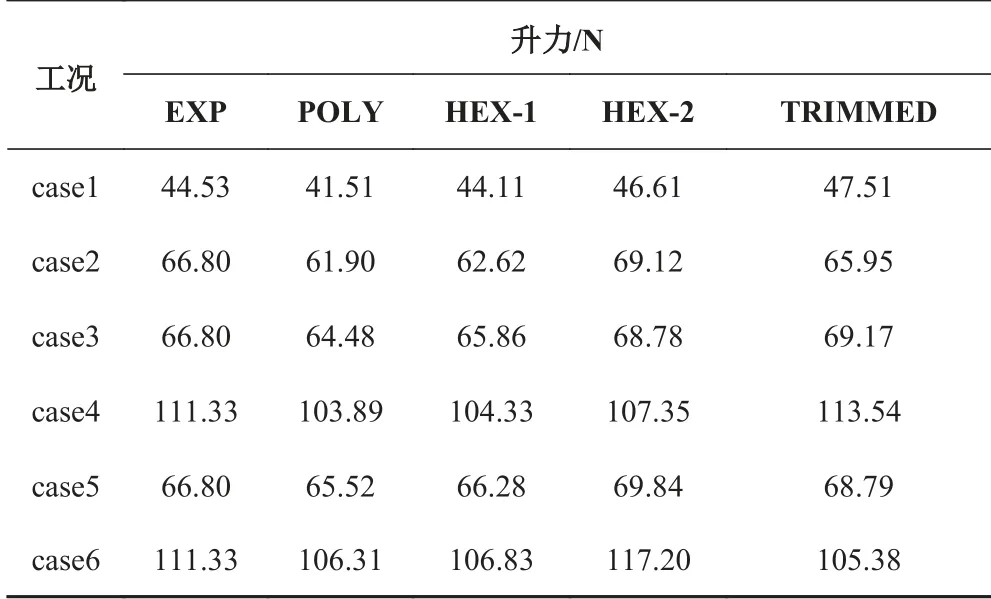
表 3 不同網格的NACA 滑行楔形體升力計算結果Tab. 3 Numerical results of lift of NACA planing wedge based on different meshes

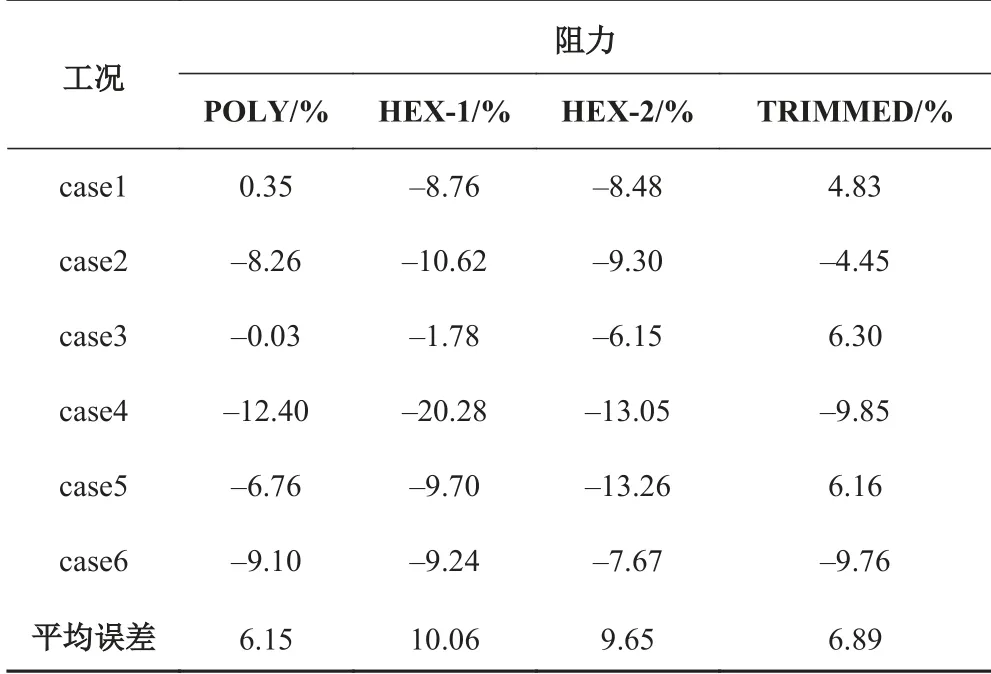
表 4 不同網格的NACA 滑行楔形體阻力計算結果誤差Tab. 4 Drag error of NACA planing wedge based on different meshes

在基于切割體網格、嘗試使用STAR CCM 作為求解器對某一細長尖肶滑行艇進行數值仿真計算時遇到了偽擴散問題，表現為船體濕表面處的水組分值應為1 的地方卻小于1。但在使用多面體網格（填充隨體區域）和六面體網格（填充靜止區域）構成的混合網格并利用FLuent 求解時未遇到偽擴散問題，船底濕表面處水組分值為1，如圖4 所示。在研究過程中發現，通過合理設置第一層網格的高度和選擇合適的壁面函數可以改善基于切割體網格的偽擴散問題，但不能完全解決。為了驗證多面體網格改善偽擴散的能力，對比不同yplus 下，Fn=1.63 時分別基于切割體網格和多面體網格的船體表面水組分分布及阻力預報結果。網格采用上一節中的設置，區別在于隨體區域分別由切割體網格填充和由多面體網格填充。船體固定，姿態設置為基于四面體網格給出的預報值。計算基于求解非穩態RANS 方程。

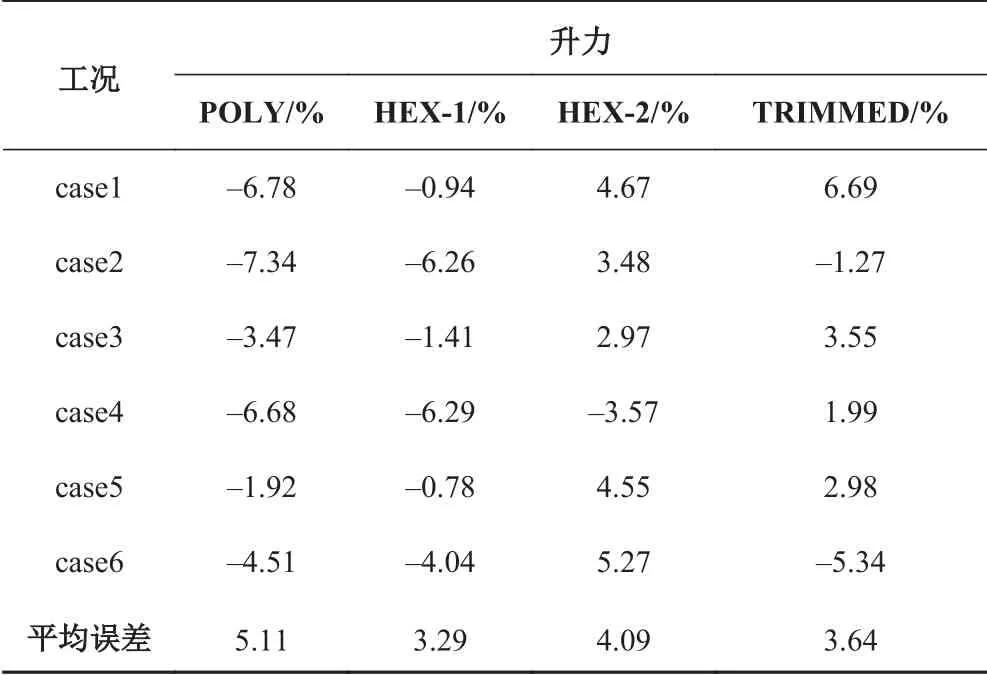
表 5 不同網格的NACA 滑行楔形體升力計算結果誤差Tab. 5 Lift error of NACA planing wedge based on different meshes

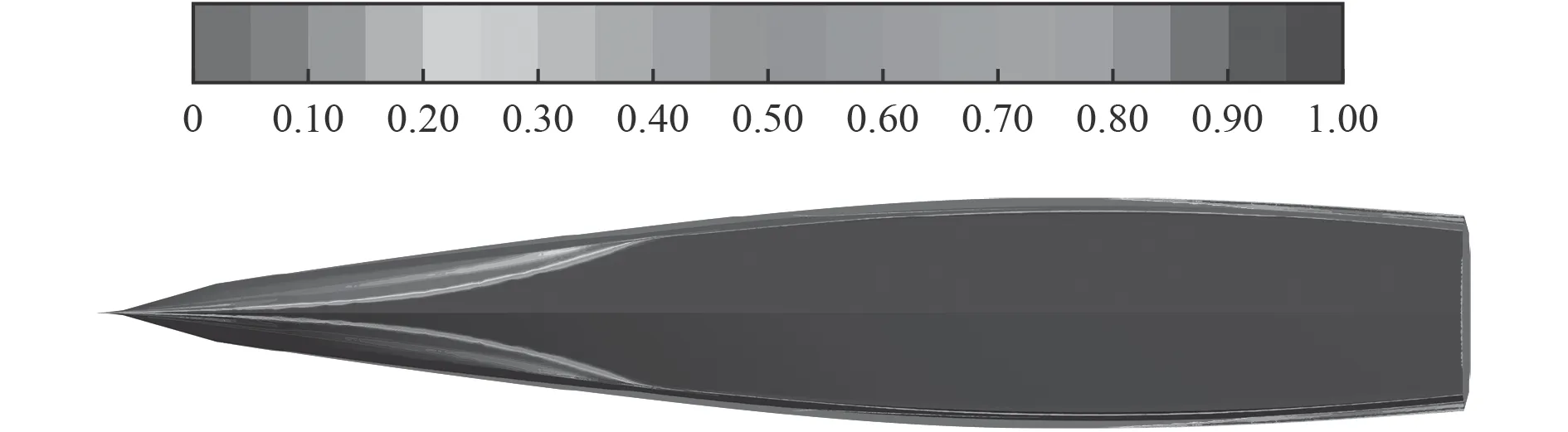
圖 4 基于多面體網格的船體表面水組分分布Fig. 4 Volume fraction of water on the hull bottom predicted by polyhedral mesh

由圖5 可知，不同yplus 下切割體網格對偽擴散的敏感性要明顯高于多面體網格。對比工況a 和工況b，可見在壁面函數選擇和yplus 值分布區間不合理時，基于多面體網格的數值仿真計算仍然給出了合理的船底水組分分布，而基于切割體網格的數值仿真計算則出現了嚴重的偽擴散。水組分分布直接影響了摩擦阻力的預報。由表6 可知，工況a 所得的摩擦阻力系數遠小于其他工況所得的摩擦阻力系數。當選合理選擇壁面函數和yplus 值分布區間時，基于切割體網格的數值仿真計算遇到的偽擴散問題有很大改善，但是沒有徹底消除。而基于多面體網格的數值仿真計算未遇到偽擴散的問題，對偽擴散不敏感。因此在不能很好確定流場狀況及第一層網格高度的情況下，使用多面體網格可以減小預報誤差。此外，本文研究結果也同文獻[7]中提到的多面體網格對WSS（wall shear stress）的計算更準確形成呼應。

圖 5 不同yplus 下的基于多面體網格和切割體網格船底面水組分分布Fig. 5 Volume fraction of water on the hull bottom predicted by polyhedral and trimmed meshes under different yplus

表 6 不同工況下網格參數及阻力系數Tab. 6 Mesh information and drag coefficient of different cases

3 結 語

本文研究得到以下結論：

1）基于多面體網格的滑行艇數值仿真計算具有相當高的精度，完全滿足工程需要；

2）多面體可以改善滑行艇仿真計算中遇到的偽擴散問題。通過對比切割體網格可知，基于多面網格的滑行艇的數值計算對偽擴散問題不敏感。對于一些具有復雜外形設計、難以使用六面體網格計算域填充的滑行艇仿真案例，若使用切割網格遇到偽擴散問題時則可以考慮使用多面體網格，或者直接使用多面體網格填充隨體區域來嘗試解決遇到的偽擴散問題。