負浮力四傾轉推進器水下機器人姿態跟蹤控制
王 濤,吳 超,葛 彤
(上海交通大學 船舶海洋與建筑工程學院,上海 200240)
0 引 言
在最近的幾十年中,大量的海洋探索工具被開發出來,擴展了人類的研究范圍,獲得了關于海洋的更多知識,使得深海的礦藏能夠得到有效利用[1–2]。其中,AUV(Autonomous underwater vehicle)是一種廣泛使用的潛水器,它有高速和活動范圍大的優勢[3–4]。大部分AUV 在水中是中性浮力的,為了維持中性浮力,AUV 需要安裝很多浮力材料,增加了AUV 的體積及AUV 在水中航行時的阻力。
本文針對一種負浮力四傾轉推進器AUV(negative-buoyancy quad tilt-rotor autonomous underwater vehicle,NQTAUV),進行了抗干擾姿態跟蹤控制設計。NQTAUV 沒有安裝浮力材料,因此在水中有剩余重量。NQTAUV 質量為 m ,浸沒于水中受到浮力為 B,且滿足 B <mg, g為重力加速度。有懸停、傾轉、水平巡航3 種工作模式。在懸停模式下,依靠垂直向下的推進器產生升力克服剩余重量;在傾轉模式下,推進器由垂直向下旋轉至朝向后方,推動AUV不斷水平加速。NQTAUV 安裝有水翼,隨著水平分量推力的增加,AUV 速度加快,機翼產生的流體升力克服水中剩余重量[5–6],實現水平巡航。
NQTAUV 有獨特的機身傾轉懸停(body-tilt-hover,BTH)功能,即在機身實現大幅度俯仰角機動的時候,能夠懸停在水中一個位置點,而不產生水平的分力,不會引起水平的位移。對于普通AUV 來說,一般是在艇體尾部有一個推進器,部分在艇體上還有垂向和橫向的推進器,實現垂向和水平機動。不過,這些推進器一般固定在艇體上,只能提供固定方向的力或力矩,不能提供矢量推力,所以不能做機身傾轉懸停。然而,NQTAUV 可以借助自身的矢量推力進行機身傾轉懸停[7–8]。BTH 是一項有用的功能。比如,AUV 前部一般安裝有攝像機,用以提供視頻信息。通常來講,為了更大的視角,攝像機安裝在一個二自由度云臺上。然而,當云臺損壞后,相機的視角被限制,此時,可以采用BTH 功能,操作手可以重新獲得原來的視角。不過,當工作在BTH 模式時,因為舵機會隨著俯仰角而轉動,引起轉動慣量的變化,同時產生一定的干擾力矩,且不能計算或測量得到干擾量幅值。因此,需要更魯棒的姿態控制器,實現姿態的跟蹤。此外,在BTH 模式下,水動力矩也會隨著機身的旋轉運動而改變。因此,研究干擾的估計和補償策略,以及在干擾下的姿態跟蹤,是符合實際應用需要的。
為了進行干擾下的控制,學者們進行了大量研究。Li[9]設計了四自由度非線性滑動狀態觀測器,建立了ROV 的洋流模型和簡化的臍帶干擾力模型,基于簡化的索力模型表征電纜的干擾力,并實時估計纜的干擾力,提高了觀測精度,減少了抖振。Yuan[10]設計了一種非線性自抗擾控制方案控制氣動肌肉執行器,采用連續離散擴展狀態觀測器估計總擾動,然后使用非線性復合控制器,在氣動平臺上進行了實驗,驗證了整個系統的可控性。Cui[11]對路徑跟蹤問題,設計了自適應神經網絡控制器,考慮了外部干擾、控制輸入非線性和模型不確定性等因素。Liu[12]用非線性干擾觀測器估算了作用在飛行器上的風效應,然后將風信息與控制器結合,設計了一種抗干擾導航算法,實現風干擾下的實時路徑跟蹤,并理論分析了復合控制器的全局漸近穩定性,進行了軟件在環的仿真。對小型飛機進行的飛行仿真試驗,驗證了其性能。可以看出,在以往的研究中,對于干擾觀測的研究取得了大量進展,部分控制器的穩定性得到了證明。不過,這些算法在實際應用中存在調參數量多的問題,不利于控制器實際的部署和調整。
姿態跟蹤控制是NQTAUV 的重要功能,一般作為路徑跟蹤等更高一級控制的內環,它的性能決定了上層控制的精度[13]。干擾力矩對姿態控制精度影響很大,為了補償干擾對姿態跟蹤控制的影響,設計調試簡單,易于部署的抗干擾控制器,本文提出了基于干擾觀測器的姿態跟蹤控制器設計框架,并進行了姿態跟蹤實驗。
首先,基于修正的羅德里格斯參數(modified Rodrigues parameters, MRPs)姿態表示法建立NQTAUV 的運動學和動力學模型,并進一步推導出姿態跟蹤誤差模型。其次,設計干擾觀測器,估計作用在姿態上的干擾;設計姿態跟蹤控制系統,并證明控制系統的穩定性。最后,進行實時姿態跟蹤實驗,驗證了所提方法的控制性能。
1 NQTAUV 數學模型
1.1 運動學和動力學
在姿態跟蹤控制中用到了3 個坐標系:地球坐標系 Fe、 本體坐標系 Fb和目標坐標系 Fd。坐標系示意圖如圖1 所示。
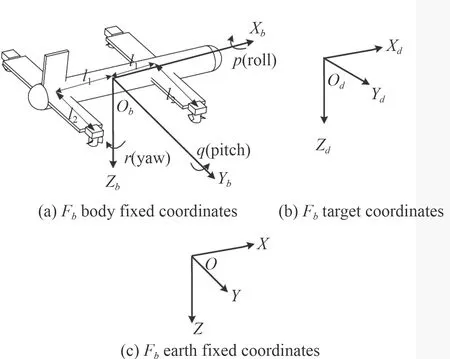
圖 1 坐標系Fig. 1 Coordinates
BTH 模式示意圖如圖2 所示。
表示剛體姿態的方法有多種,其中歐拉角是三參數姿態表示法,因為簡單、直觀,被廣泛應用。然而,歐拉角在 ±90°有奇異;MPRs 也是三參數姿態表示法,不過在 ± 180°才有奇異點,能夠表示更大范圍的機動[14]。因此,本文選取MRPs 表示姿態。

圖 2 機身傾轉懸停模式Fig. 2 Body-tilt-hover mode
NQTAUV 的運動學和動力學方程為:
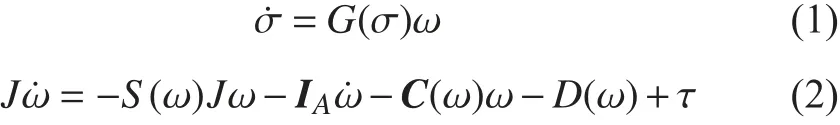
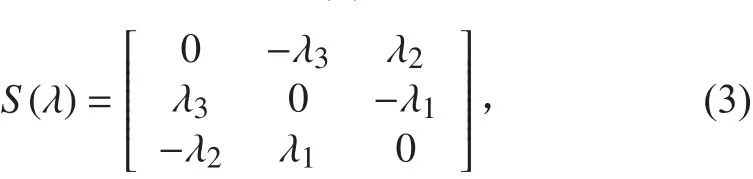
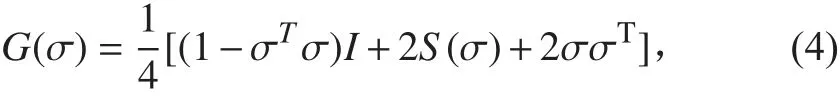
G(σ)有性質:
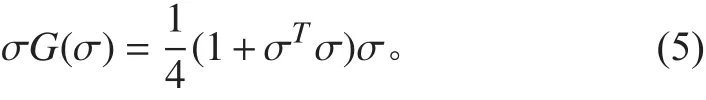
1.2 姿態跟蹤誤差模型
在姿態跟蹤問題中,定義目標姿態 [σd,ωd,ω˙d],因此,相對姿態就是:
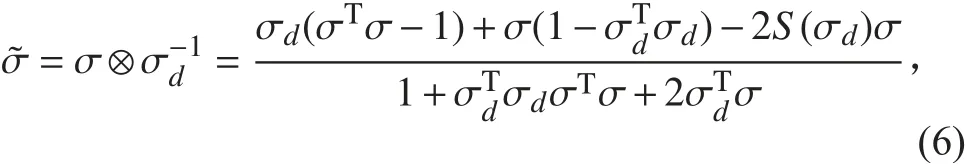
相對角速度為:

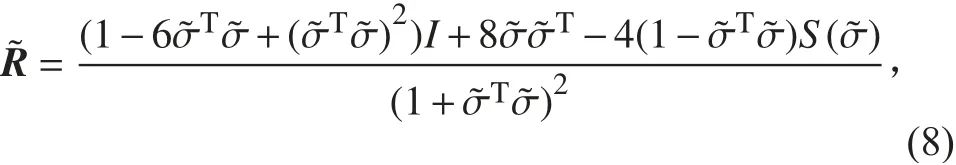

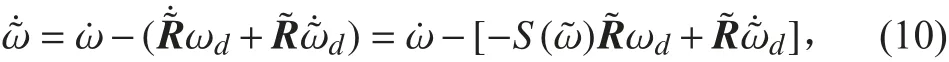
因此,姿態跟蹤誤差模型為:
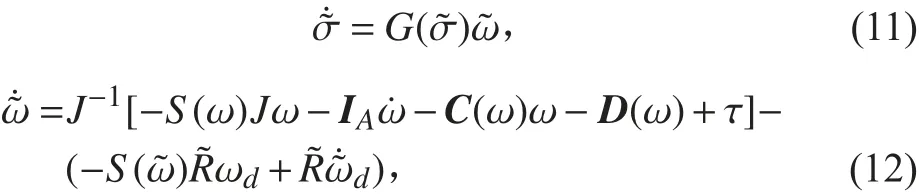
用反饋線性化消去系統動態中的非線性項:
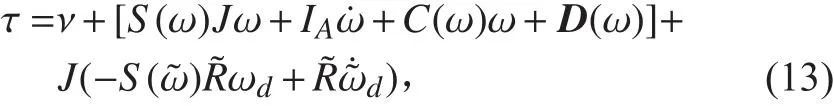
其中, ν是要設計的控制量,那么公式(12)變成:

其中: d 為干擾,且 d 來源于很多方面。首先,推進器的旋轉會對俯仰產生干擾力矩;其次,當NQTAUV在水中水平巡航的時候,水翼也會產生額外的力和力矩。在沒有速度傳感器的情況下,水動力矩不能被準確計算。在此,將所有干擾當做一個復合的干擾,估計這個復合干擾 d 。記d′=J-1d,方程(14)變成:

2 控制器和干擾觀測器設計
基于干擾觀測器的控制框架如圖3 所示。

圖 3 控制框架Fig. 3 Control scheme
2.1 干擾觀測器設計
作用在NQTAUV 上的干擾不能被直接測量,因此需要引入干擾觀測器估計這個干擾。假設干擾是常值,記的估計,估計誤差記為。基于方程(15),設計干擾觀測器為:
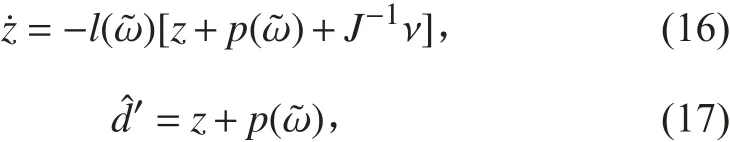

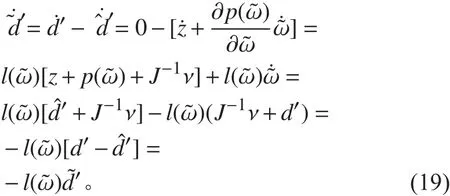
同時,因為 ,故得到:


故得到:

2.2 控制器設計
選取李雅普諾夫函數:
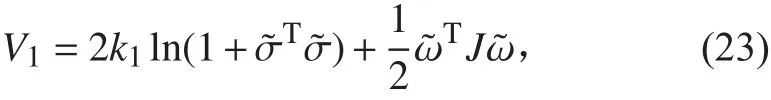
其中 k1>0 , V1的導數為:
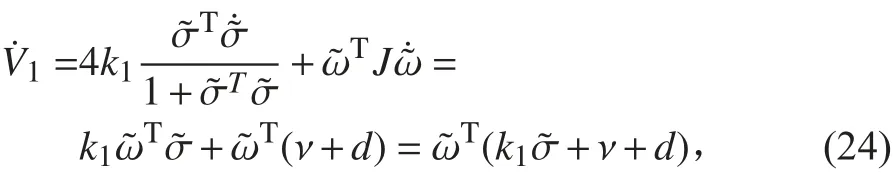

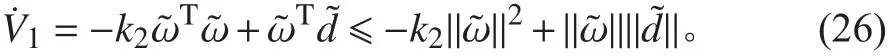
2.3 穩定性分析
用李雅普諾夫穩定性理論分析整個系統的穩定性。選取李雅普諾夫函數:

V2的導數為:

又選取李雅普諾夫函數 求導得到:

選取 k2,k3, 滿足,則。故由李雅普諾夫穩定性理論,系統是全局漸進穩定的。
3 實驗結果和分析
3.1 測試平臺
實驗采用浸入水中的三自由度測試平臺進行。NQTAUV 本體通過一個球鉸連接在固定的基座上,使得本體能夠實現俯仰和橫搖各 ±30°的活動范圍,首向角可實現 360°的活動范圍。傾轉推進器可以進行360°的旋轉,最大旋轉速度6.9 rad/s,最大提供1 5 N的推力。姿態傳感器采用MPU9250,提供三軸的角速度、加速度和磁場強度,經過卡爾曼濾波融合后得到姿態角和角速度。控制電路板采用STM32 F401RE,具有512 kB 內存,84 MHz頻率。控制器控制頻率為100 Hz。NQTAUV 的機械參數見表1。

表 1 NQTAUV 機械參數Tab. 1 Mechanical parameters of the NQTAUV
3.2 姿態跟蹤實驗
控制器和觀測器參數選取為k1=3.58,k2=0.67,k3=10。對于BTH 模式,典型姿態跟蹤測試信號是俯仰軸的正弦信號,因此,定義目標姿態正弦信號為:
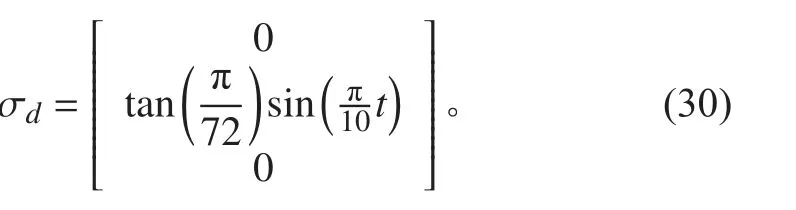
在 x 和 y 軸施加約0.008 N.m 的常值干擾力矩。為了驗證所提干擾觀測器和姿態跟蹤控制器的有效性,在實驗的 0 ~50 s 內,將干擾觀測器關閉;在 5 0 ~100 s內,將干擾觀測器激活。實驗結果如圖4~圖6 所示。其中,圖4 顯示姿態跟蹤效果,圖5 顯示控制力矩,圖6顯示干擾估計值。
從圖4 可以看出,當干擾觀測器關閉時,能跟蹤正弦跟蹤信號,但是會產生大約0.02 的姿態偏移量,且有大約1 s 的相位滯后。同時可以看出,姿態波動幅值很大,說明受干擾影響很大。當干擾觀測器激活后,姿態偏移量為0,相位滯后也被消除,姿態波動非常小,說明干擾被補償掉,實際姿態能夠精確跟蹤目標姿態。
從圖5 可以看出,在激活干擾觀測器后,控制輸出有一個整體的增加,說明對常值干擾力矩進行了補償。
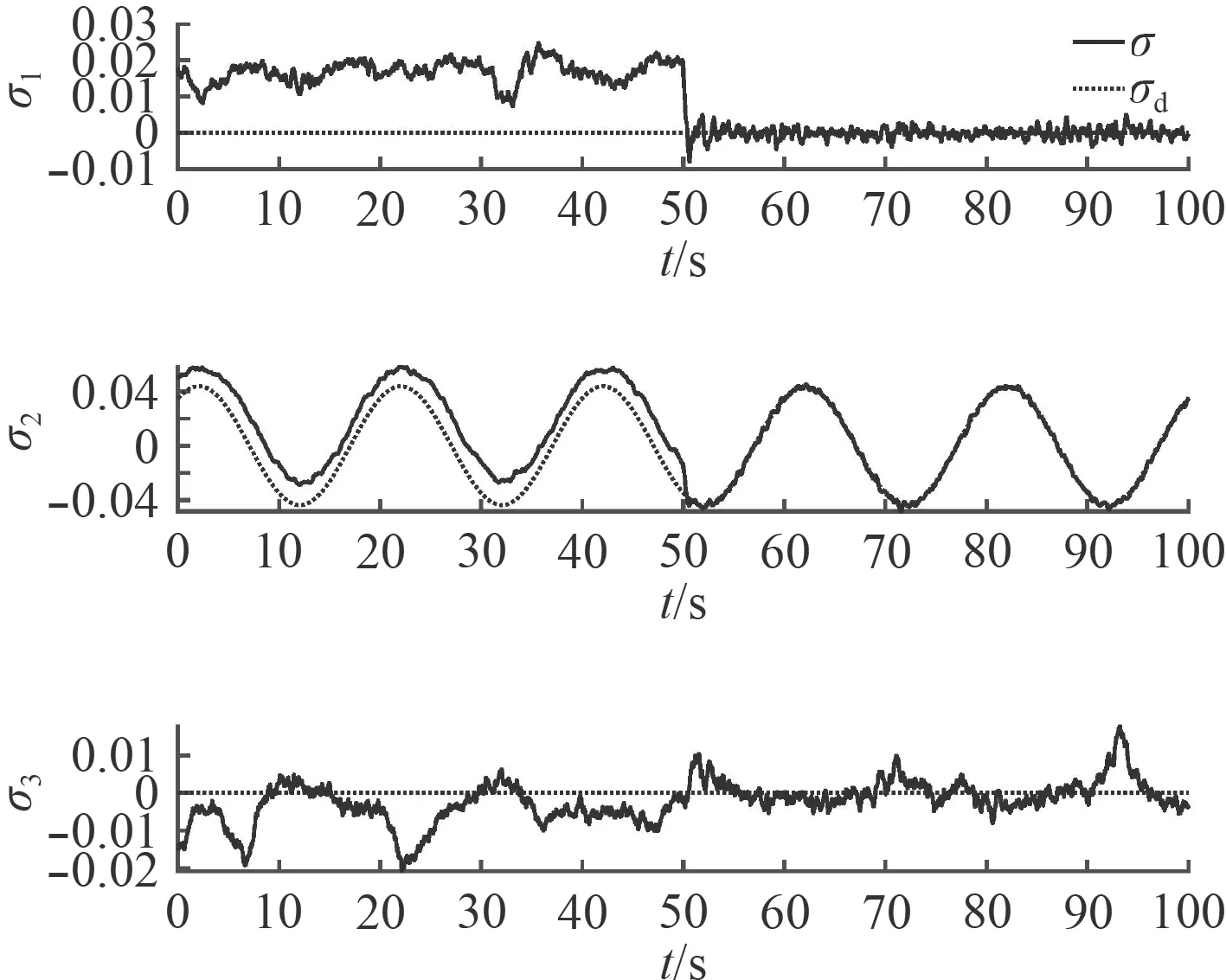
圖 4 正弦信號姿態跟蹤結果Fig. 4 Sinusoidal attitude tracking performance
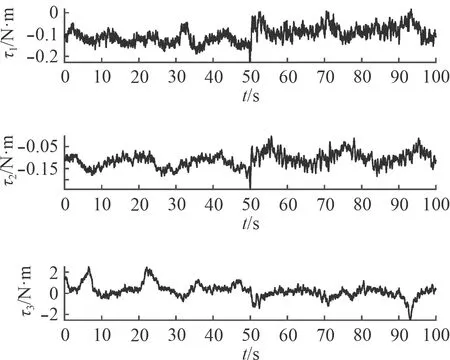
圖 5 控制輸入Fig. 5 Control input
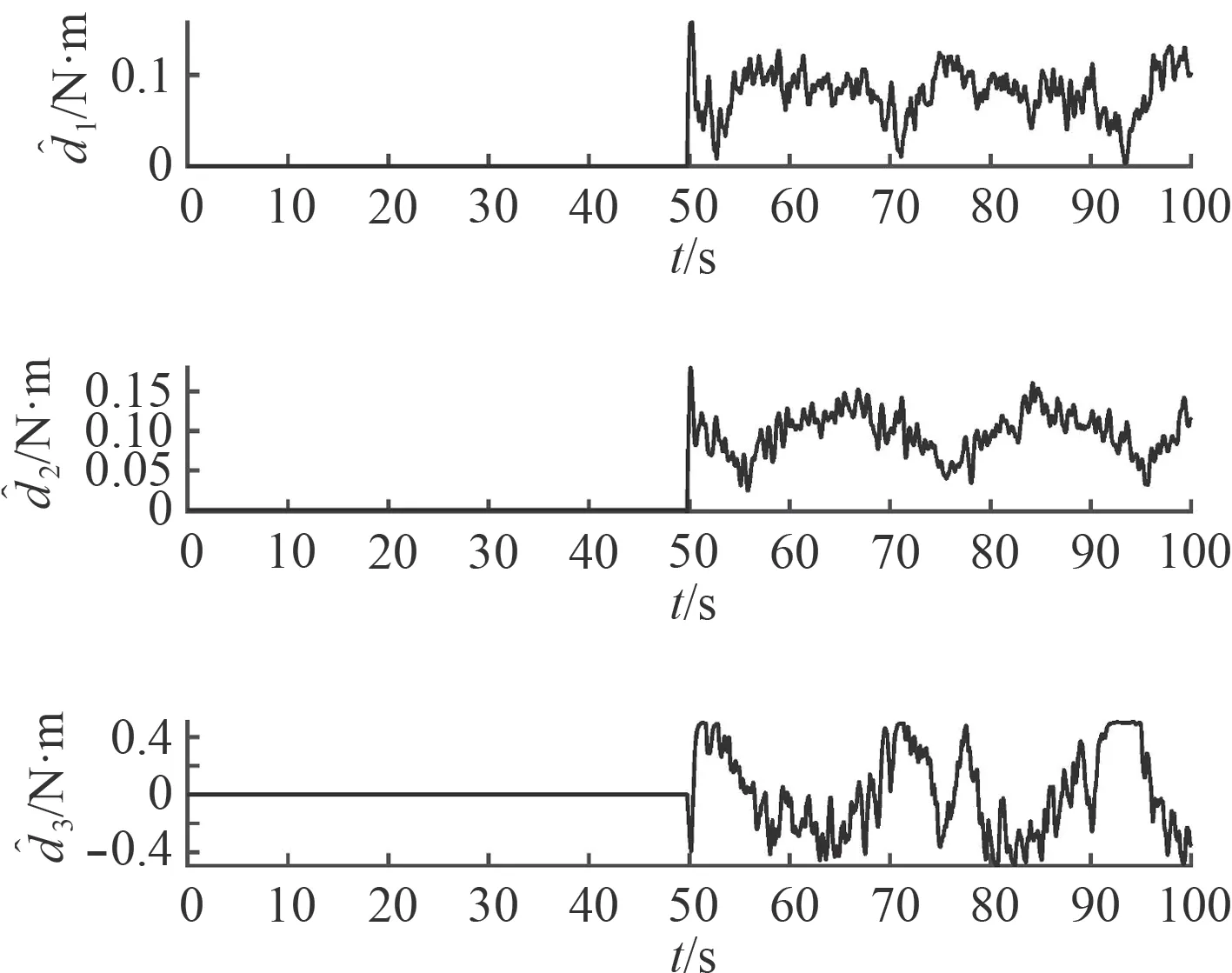
圖 6 干擾觀測值Fig. 6 Disturbance estimation
從圖6 可以看出,當干擾觀測器激活后,干擾估計值呈現波動,與正弦信號相位相吻合。在正弦姿態跟蹤時,NQTAUV 受到周期性的水動力,其周期和相位與本體運動相同,由于目標姿態信號周期為20 s,因此這是緩慢變化的干擾。這也說明干擾觀測器不但可以估計常值干擾,還可以估計緩慢變化的干擾。
綜上,干擾觀測器能夠準確估計常值干擾,對緩慢變化的干擾也有準確的估計。所提的姿態跟蹤控制器能夠準確跟蹤目標姿態。
4 結 語
本文針對負浮力四傾轉推進器水下機器人,設計了抗干擾控制框架。基于修正的羅德里格斯參數,導出了負浮力四傾轉推進器水下機器人姿態跟蹤的數學模型。然后設計了干擾觀測器來估計干擾,并基于此干擾觀測器設計了姿態跟蹤控制器。控制框架的穩定性得到了證明。最后,通過實時姿態跟蹤實驗,比較干擾觀測器激活和關閉2 種不同情況下的姿態跟蹤表現,驗證了控制框架的性能。所提出的基于干擾觀測器的控制框架,抗干擾能力強,參數數量少,調節簡單,易于實際部署。

