半參數模型在開采沉陷預計中的應用
成 樞 朱玉明 馬衛驕 高秀明 劉忠偉
(1.山東科技大學測繪科學與工程學院,山東青島266590;2.山東省核工業二四八地質大隊,山東青島266041;3.山東泰豐控股集團有限公司王家寨煤礦,山東泰安271204)
由于參數模型具有很強的假設性,需要滿足一些假設條件,比如:觀測誤差中只有偶然誤差,平差模型線性化后的微小量可忽略不計等。所以,當參數假定與實際偏差較大時,平差模型的參數估值精度降低。由于參數模型的局限性,相關學者引入非參數模型理論。非參數模型取消了變量之間在函數關系形式上的假設,其函數模型表示任意的函數關系,因此放寬了函數形式的限制[1-3],但是非參數模型的模型解釋能力較低且觀測數據的維度受到限制。因此,針對參數模型與非參數模型各自的局限性,相關學者將二者結合到一起構建了半參數模型。
在20世紀80年代,Engle等針對氣候條件改變對電力需求變化的影響提出了半參數模型[4-6]。半參數模型作為一種重要的統計模型,數學模型中包含參數部分與非參數部分,克服了單一的參數模型與非參數模型的不足[7]。當觀測值中存在無法忽略的模型誤差時,半參數模型在數學模型方面相對于參數模型更符合客觀實際;在數值求解方面可以分別求解參數向量、非參數向量和偶然誤差,因此被廣泛應用于測量數據處理中。
本研究采用礦區地表沉降實測數據建立半參數灰色Verhulst 模型,考慮到模型誤差問題,灰色Verhulst 模型的時間響應序列的系數求取可以采用半參數模型,根據半參數模型估值準則設計不同計算方案構建半參數灰色Verhulst 模型,求解時間響應序列中的參數,并進行沉降預計結果對比和精度分析。
1 半參數灰色Verhulst模型
1.1 半參數模型
通常影響觀測值的因素有很多,然而經典平差模型不考慮系統誤差與粗差的影響。當模型誤差無法忽略且其性態十分復雜時,可以在函數模型中加入一個待定量,用來描述觀測量與影響因素之間函數關系不明確的部分,這種平差模型即為半參數模型[4,7]。
半參數模型的函數模型和隨機模型分別為
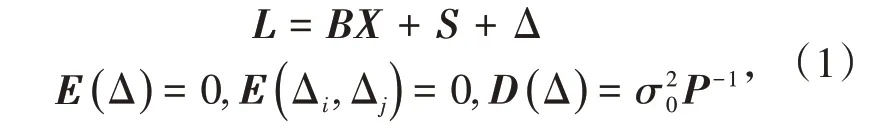
式中,L 為n 維觀測向量;X 為t 維參數向量;B 為列滿秩設計矩陣;S 為n 維非參數向量;Δ 為n 維誤差向量;為方差因子;P為Δ的權矩陣。
半參數模型在函數模型表達式中添加了非參數部分,相對于參數模型而言,在模型誤差無法忽略時,半參數模型具有更大的優越性:在模型建立方面,數學模型與客觀實際更為接近;在數值解算方面,可求出模型誤差與偶然誤差。
由式(1)可知,半參數模型的誤差方程為
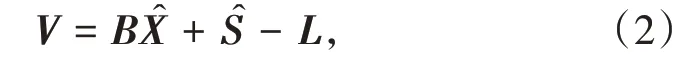
在最小二乘準則VTPV=min 下構造條件極值函數得到的法方程為
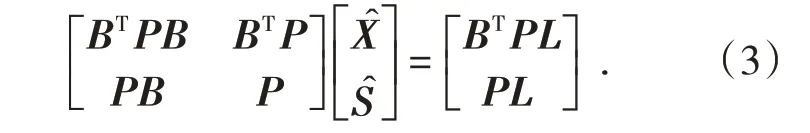
由于待定參數個數多于誤差方程個數,因此基于最小二乘準則構建的半參數模型的法方程唯一解不存在,需要在VTPV=min基礎上附加最優化準則,構成補償最小二乘法則[8]:
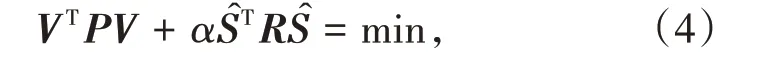
式中,R 為正則矩陣;α 為正則化參數(或稱為平滑因子),其主要作用是在極小化過程中,在二次型VTPV和起到平衡作用[9-10]。
根據式(2)和式(4)以及構造條件極值的拉格朗日乘數法,構造的目標函數為
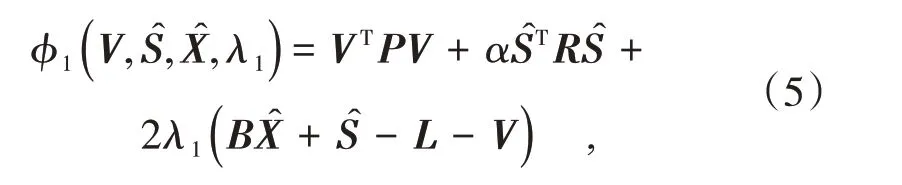
式中,λ1為拉格朗日常數。
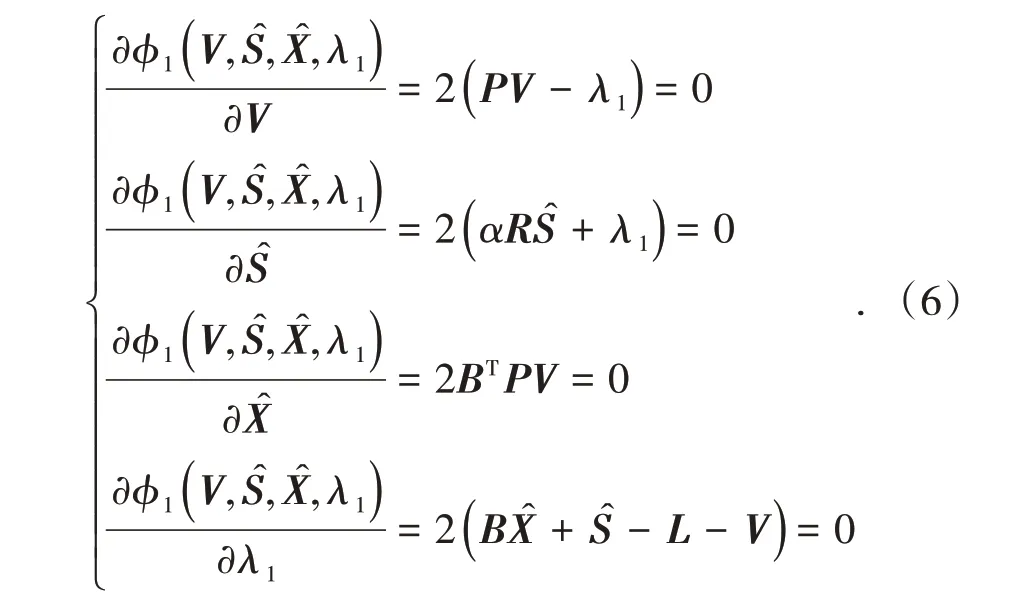
由式(6)可得:
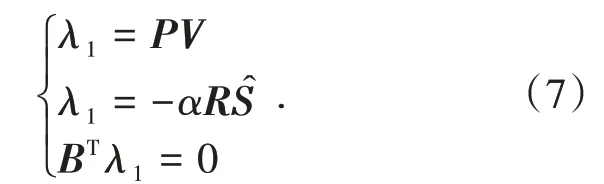
結合式(2)和式(7),可得到基于補償最小二乘估計準則的半參數模型誤差方程的法方程:
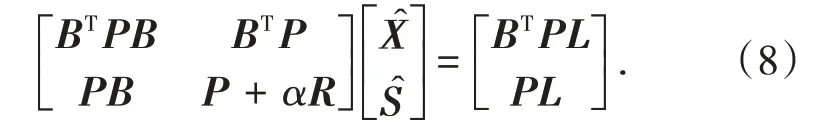
由于矩陣R為正定矩陣,因此基于補償最小二乘估計構建的法方程是正定可逆矩陣,法方程有唯一解,對式(8)求解可得:
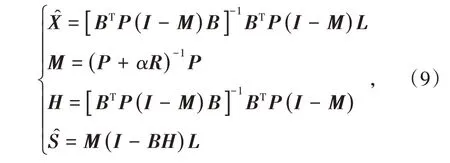
式中,M為光滑矩陣;H為帽子矩陣。
正則矩陣選取根據實際情況,構造方法一般有時間序列法、距離法和樣條函數法等;正則矩陣選取一般有L曲線法、信噪比值法、效率法等[7,12]。
當法方程系數矩陣接近奇異時,應當采用半參數嶺估計準則:
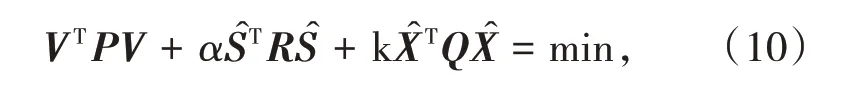
式中,k 是在X 與V 的正則化參數,稱為嶺參數,嶺參數的構造方法一般有L曲線法[7,13]、U曲線法[14-15]等,參數求解方法與式(6)相同,在此不做贅述;Q一般取單位矩陣。
1.2 灰色Verhulst模型
設原始監測數據序列為
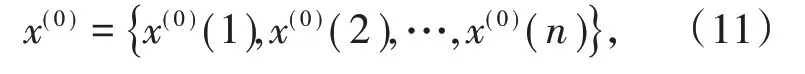
通過原始數據累加弱化原始數據序列的波動性和隨機性,生成1-AGO序列

根據GM(1,1)模型的建模方法,得到灰色Verhulst模型的一階白化非線性微分模型為

式中,a,b為灰色Verhulst模型待計算參數。
若按最小二乘法,解得待求參數估值為
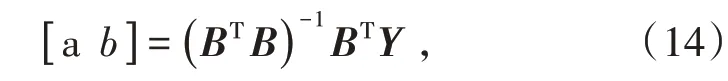
將參數估值a,b 代入微分方程求解得到灰色Verhulst模型的時間響應序列[16]:

最后還原數列得到模型的預測值:
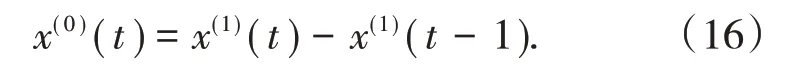
從測量平差的角度分析,式(14)求取待求參數與參數平差的法方程求解形式相同。在只考慮偶然誤差的情況下,可以采用最小二乘準則求解灰色Verhulst 模型一階白化非線性微分方程中的參數最優估值。若模型誤差不可忽略,可考慮采用半參數模型求解一階白化非線性微分方程的參數估值,進而建立半參數灰色Verhulst模型進行預計。
1.3 半參數灰色Verhulst模型檢驗
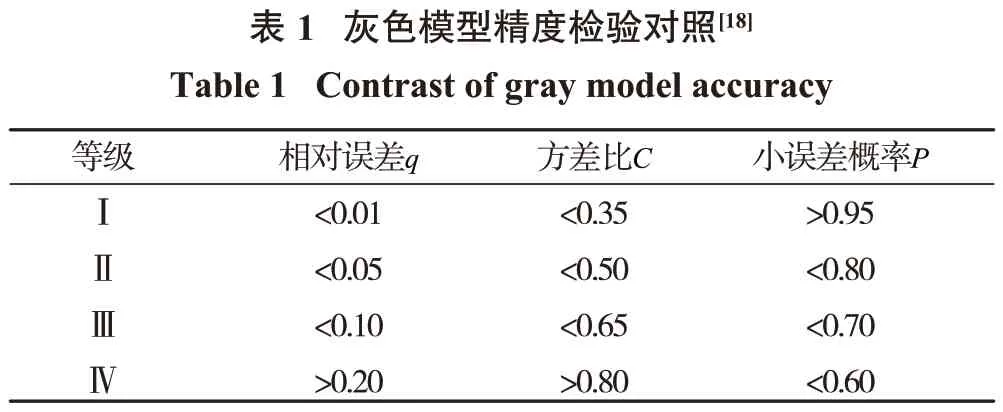
建立半參數灰色Verhulst 模型時應當進行模型檢驗,驗證所建立的模型是否符合實際情況。半參數灰色Verhulst 模型檢驗主要包括采用半參數模型求解一階白化非線性微分方程中參數估值的假設檢驗以及灰色模型的精度檢驗。其中,半參數模型檢驗采用線性假設法[17],灰色模型精度檢驗結果等級劃分如表1所示[18]。
?
2 算例分析
2.1 試驗數據
以某礦區地表沉降監測為例,跟據相關設計,礦區九采區共有5 個回采工作面,其中,7265 工作面回采走向長度D1=909 m,傾向長度D2=186 m,煤層厚度m=4.15 m,煤層傾角θ=0~12°(平均7°),傾斜面積168 334 m2,工業儲量106 萬t,工作面標高-678~-743 m,地面高程34.1~37.5 m,2017年2月中旬開采,2018 年1 月12 日回采結束,回采量88.2 萬t,回采率85%。
依據《測量規程》和“三下”開采規范,結合九采區的覆巖巖性,選取巖移角值參數布設觀測線。
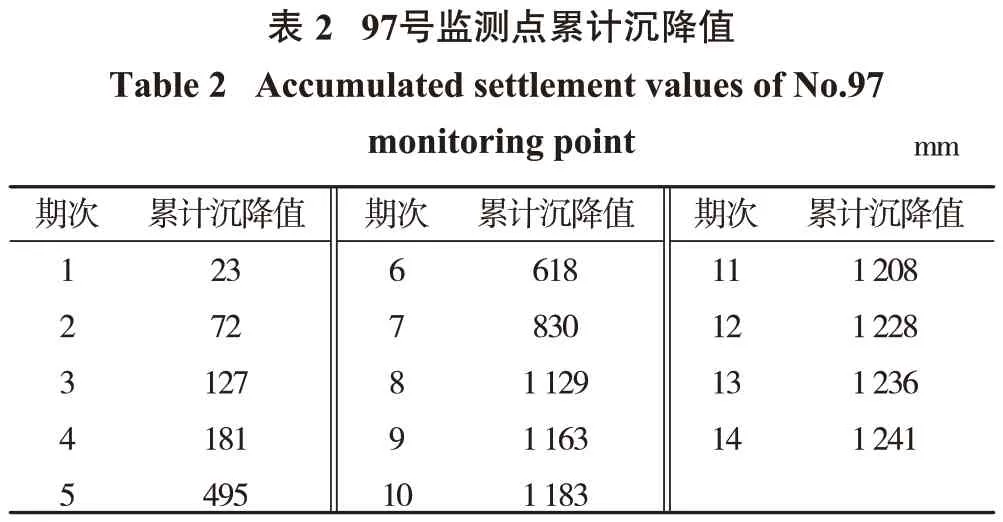
7265 工作面觀測期間,觀測站97 號測點具有最大下沉速度Vmax,最大下沉值達到Wmax=1 241 mm。選取97 號沉降監測點的14 期觀測數據得到的累計沉降值W(表2)建立預計模型。以原始數據為基礎建立預計模型,并以最后4期數據進行預計值與實際值對比,作為精度檢核依據。
?
2.2 計算結果對比及分析
若根據礦區沉降實測數據建立半參數灰色Verhulst 模型,首先要判定系數矩陣B 的復共線性[19-20]。經計算,系數矩陣B 存在較強的復共線性,因此半參數模型中估值準則只需要考慮半參數嶺估計準則。
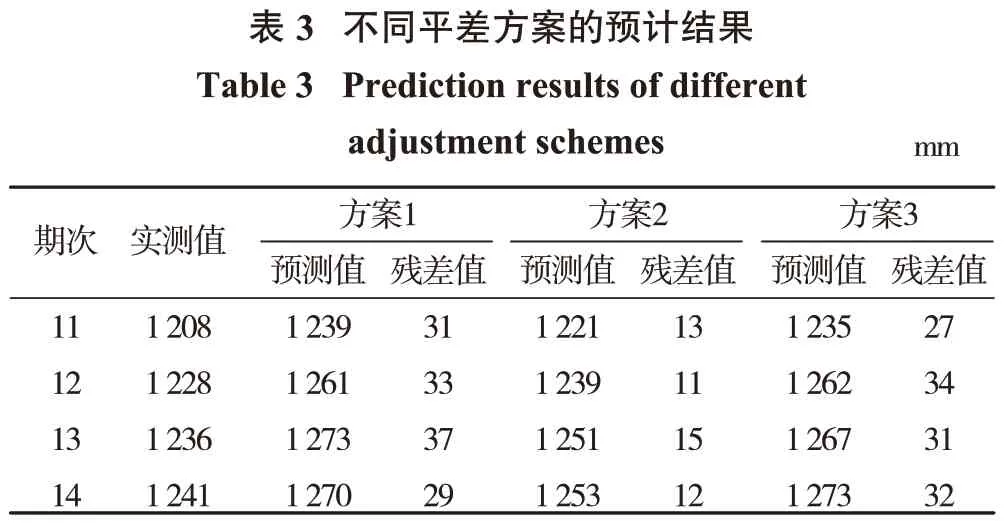
基于半參數灰色Verhulst 模型在無粗差數據時設計了以下3種計算方案:①灰色Verhulst模型;②半參數灰色Verhulst 模型,其中正則矩陣采用時間序列一階差分法;③半參數灰色Verhulst 模型,其中正則矩陣采用時間序列二階差分法。正則化參數按Xu函數法確定取值α=2.436,嶺參數按U 曲線法確定取值k=0.334。經過不同方案計算,并以最后4 期的實測值作為預計效果的評價標準,得到了不同平差模型的預計結果以及殘差值如表3所示。
?
由表3可知:通過采用不同半參數回歸模型對97號監測點進行累計沉降預計時,方案1預計誤差絕對值的最大值為33 mm,方案2 預計誤差絕對值的最大值為15 mm,方案3 預計誤差絕對值的最大值為34 mm,3 種方案的均方誤差經計算分別為37.68 mm、14.82 mm 和35.92 mm。因此方案2 建立的半參數灰色Verhulst 模型求取時間響應式參數的精度最高,在3 種方案中的均方誤差最小,相應的預計下沉曲線更加符合實測數據的變化趨勢。
由表3 中方案2 和方案3 對比可知:當正則矩陣采用時間序列法確定時,方案2得到的預計結果優于方案3。因此,本次實測數據中采用半參數模型的估值準則計算灰色Verhulst 模型一階白化非線性微分方程的待求參數時,應選擇時間序列一階差分法確定的正則矩陣。
在上述分析的基礎上,本研究進一步對實測數據進行半參數模型檢驗與灰色模型精度檢驗。由線性假設法計算可知,統計量F=87.642。由F分布表可知:F >F0.05( 14, 13 )>F0.05( 15, 13 )=2.53,因此非參數向量S 為非零向量。同時,經計算相對誤差q=0.032,方差比C=0.394,小誤差概率P=0.615,對照灰色模型精度檢驗表(表1)可知:灰色模型精度滿足Ⅱ級(優)標準。因此,礦區地表沉降實測數據適用于構建半參數灰色Verhulst模型。
3 結 語
采用礦區沉降實測數據進行了半參數灰色Verhulst 模型的算法驗證,基于半參數模型理論和礦區沉降實測數據建立了半參數灰色Verhulst 模型。針對灰色Verhulst 模型的時間響應序列的系數求取問題,根據正則矩陣、正則化參數以及嶺參數的選取方法,設計了多種方案計算半參數灰色Verhulst 模型的參數估值,并進行了沉降預計結果對比和精度分析。在上述分析的基礎上,采用模擬數據與礦區沉降實測數據進行了模型檢驗。檢驗結果表明:礦區沉降實測數據適用于半參數灰色Verhulst 模型。實際應用中,關于地表沉陷動態預計的時間函數還有Knothe時間函數、Logistic 時間函數等,對于不同地表沉陷動態預計的時間函數可進行進一步討論。

