凸輪軸升程型線的GUI界面開發

周少甫

（武漢理工大學，湖北 武漢 430000）

由于凸輪輪廓不是簡單地由多段圓弧和直線組成，而是一段比較復雜的曲線方程。工業上一般用專業設備測量得到離散點數據，然后再按各種數控機床的不同需求（功能指令代碼和程序格式及插補方式等）進行后續處理，編出加工程序。這種方法編程困難，工作量大，精度低，效率低下。

針對以上問題，筆者用Matlab軟件擬合工具箱中的polyfit函數，可以方便快捷地進行凸輪軸升程曲線擬合，并開發了GUI界面，方便用戶調用、操作，解決了企業加工輪廓困難的問題。

1 凸輪軸升程型線的設計

凸輪軸升程型線主要是由緩沖段、上升段、下降段等組成。下面介紹具體的設計方法。

1.1 緩沖段設計

（1）緩沖段參數。緩沖段參數主要有緩沖段高度、緩沖段速度、緩沖段包角等，具體參考值如表1所示。

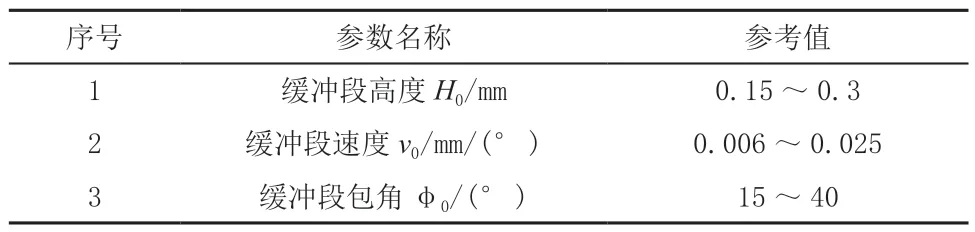
表1 凸輪升程緩沖段主要參數

式中：φC為緩沖段任意時刻的包角，0≤φC≤φ0；h0為緩沖段任用時刻的高度[1]。

1.2 上升段、下降段設計

高次方多項式凸輪軸型線。一般凸輪型線的設計都是先設計上升段，然后再通過對稱得到下降段。筆者采用六項式型線方程來擬合上升段：

式中：x為凸輪軸轉角，0≤x≤θ；y為對應凸輪轉角x的平 底挺 柱升程；C0、C2、Cp、Cq、Cr、Cs為方程各項的系數；θ為凸輪的工作段半包角；p、q、r、s是冪指數，按升冪排列，可以是任意實數，是設計變量，由設計者在設計時調節以得到理想的設計結果[2]。

2 凸輪升程型線GUI界面

文章通過Matlab的GUIDE用戶開發界面編寫子程序M文件來定義約束函數，并以回調函數方式進行調用[3]。GUI初始界面如圖1所示。此界面支持兩種邊界條件的擬合，一是“默認參數”選項，選擇此按鈕后，Matlab會從后臺直接調取系統默認的參數進行擬合，得到默認的凸輪軸升程曲線。二是用戶根據實驗或計算得到的數據，點擊“打開文件夾”按鈕，使數據加載到GUI界面，點擊“預處理”按鈕，得到速度與加速度曲線圖，判定起始、末尾分段點及包角大小，將數值分別輸入到“半包角”“升程”“起始分段點角度”“末尾分段點角度”按鈕框中，然后點擊“曲線擬合”按鈕即可獲得最終結果。完成擬合后，點擊“另存為”按鈕，程序開始以EXCEL的格式保存擬合后的數據。通過“退出”按鈕即可恢復原始界面狀態。

圖1 凸輪升程型線擬合的GUI界面

3 凸輪型線擬合

3.1 已知邊界條件的凸輪型線

根據前文論述，在AVL的TD（Time Driving）模塊中，找到多項動力擬合凸輪型線的例子，再次用其邊界條件。已知p=26q=34r=56s=60（p，q，r，s均為多項動力的冪指數），thita（半包角）=65°，v0（緩沖段末點速度）=0.016667mm/（°），Hmax（凸輪最大升程）=9.5mm，H0（緩沖段高度）=0.35mm。fay1（凸輪工作段的角度）=33°。編程運行后得到的圖像就是GUI界面中“默認參數”所編寫程序得到的圖像，如圖2所示。

3.2 給定數據后擬合的凸輪型線

圖2 由邊界條件得到的凸輪升程

工業上用專業設備測得的離散點數據，保存成數據表。先點擊“打開文件夾”按鈕，導入要擬合的數據表，然后點擊“預處理”按鈕，得到它們的速度和加速度曲線圖，如圖3所示（圖中曲線變化幅度大的為速度曲線，另一個為加速度曲線）。

由速度和加速度找到分段點，圖形發生突變的點即為分段點。由圖3可知分段點為115°和245°。這樣就知道了緩沖段和工作段的包角。

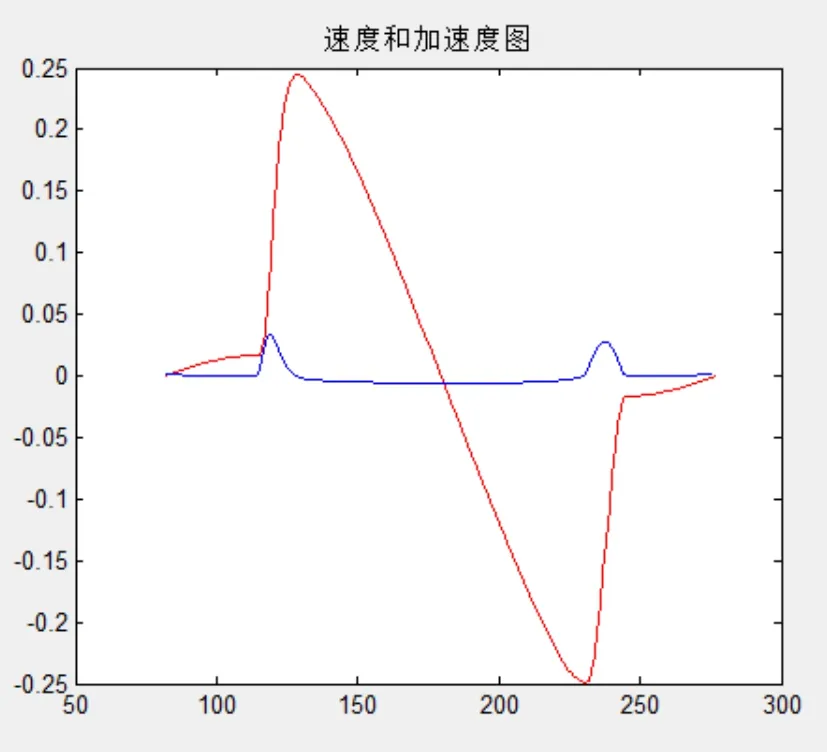
圖3 數據的速度和加速度

由最小二乘法[4-6]的指導原則：

即在數據點上的擬合值與數據值之差的平方和最小。工作段用polyfit（x,y,n）擬合，編程計算得到n=24時，s最小。緩沖段用余弦型函數擬合,得到擬合后的圖像如圖4所示。

圖4 擬合得到的凸輪升程型線

4 結束語

通過GUI界面調用程序擬合后，得到的擬合曲線基本與理論曲線重合，說明程序運行沒有問題。另外還開發了GUI進度條，使得用戶隨時把握程序運算的進度。GUI控件的應用，使得編寫Callback（回調函數）的程序可以隱藏，使得界面更加人性化和友好。由于編程語言簡單，從而可以快速方便地進行繪圖和計算，特別是矩陣的計算，相比手工插值擬合，大大提高了準確率并減少了工作量，這對于產品精準加工具有重要的意義。