基于扇區載荷的風電機組塔筒焊縫疲勞強度分析
劉建爽 李鋼強 劉祥銀 田家彬
隨著我國風電競價上網和平價上網時代的到來,塔架作為風電機組的支撐結構,具有生產周期短、可根據風電場載荷定制化設計的特點,一直以來都是風電行業研究的重點。風電機組塔架結構型式主要有圓筒式、桁架式等,按照材料類型又可分為純鋼式、混凝土式等。其中,鋼制圓筒式塔架作為主流技術被國內外風電企業大量采用。近年來,各地風電場出現的風電機組倒塌事故主要是由結構疲勞引起斷裂破壞導致的,因此,疲勞特性分析是塔架結構設計中必不可少的環節。
鋼制塔筒通過多個筒節焊接而成,焊縫的厚度直接影響塔筒結構的強度和重量。由于風電場風能資源分布具有時空變化的特點,風電機組在運行時一般采用主動偏航對風控制以達到捕捉更多風能的目的,然而這種方式導致塔筒在不同偏航扇區內承受的載荷不同。為了更精細地評估塔筒焊縫的疲勞強度,有必要考慮由于偏航對風引起的不同扇區載荷對塔筒焊縫疲勞強度的影響。
目前,國內外學者主要采用工程算法和有限元法等對風電機組塔筒進行研究。例如,使用DIN18800-4中關于應力計算的工程算法推導塔筒焊縫等效疲勞損傷計算公式,提出了等效疲勞損傷和時序疲勞損傷兩種計算方法;采用有限元法對組合式塔筒的強度和剛度進行改進分析,獲得了最佳的過渡段設計方案;基于ABAQUS協同仿真平臺對風電機組進行流固耦合分析,獲得了塔筒的內力和變形。綜合當前國內外相關文獻,還未發現考慮風電場扇區載荷影響的塔筒焊縫疲勞強度分析方面的研究。
本文對處于運行狀態的風電機組塔筒所承受的扇區湍流和載荷特性進行了詳細闡述,推導了塔筒相同高度橫截面上不同焊縫點受扇區載荷作用下的彎曲正應力計算方法,并結合雨流計數法和塔筒焊縫S-N曲線,以某2.5MW風電機組塔筒為例,獲得了分別考慮扇區和等效湍流強度的塔筒焊縫疲勞損傷。本文的研究可為風電機組塔筒焊縫疲勞設計提供一定參考。
扇區風況分析

等效湍流強度為風電機組載荷計算時通常采用的數值,但從上述推導過程中可以發現,由于風電機組所承受的扇區湍流不同,為了更精細地評估風電機組的安全性,有必要考慮不同扇區載荷對機組疲勞強度的影響。風電機組塔筒承受的載荷主要有機艙和風輪的重力、來自風輪的氣動載荷和作用在塔筒上的風載荷。其中,來自風輪的氣動載荷產生的塔筒前后方向的彎矩是影響塔筒疲勞強度的主要因素。因此,為簡化計算并避免考慮剪應力等涉及的疲勞多軸性問題,以下疲勞分析僅考慮塔筒前后方向的彎矩產生的正應力作用。
焊縫疲勞損傷
風電機組鋼制塔筒由不同的筒節焊接而成,焊縫形式主要有環焊縫和縱焊縫兩種。其中,縱焊縫與環焊縫存在交匯點,所受載荷與環焊縫基本相同,且縱焊縫疲勞等級大于環焊縫(只要環焊縫滿足疲勞強度要求,縱焊縫也就滿足要求),因此,本文僅對塔筒環焊縫進行疲勞分析。
一、焊縫彎曲正應力
當風電機組塔筒承受前后方向彎矩時,塔筒某高度橫截面處的彎曲正應力分布如圖1(a)所示,其中,塔筒橫截面一側受拉,另一側受壓。在每個扇區分別取塔筒環焊縫位于扇區中心處的焊縫點作為分析對象,即在塔筒相同高度橫截面上可按照扇區均勻選取12個焊縫點。當風電機組偏航對風運行至扇區1時,風從圖1(b)中所示的虛線方向流過,在扇區載荷作用下,每個焊縫點至中性軸的距離如圖所示,此時焊縫點H1和H7至中性軸的距離y1和y7最長,焊縫點H4和H10至中性軸的距離y4和y10最短,為零。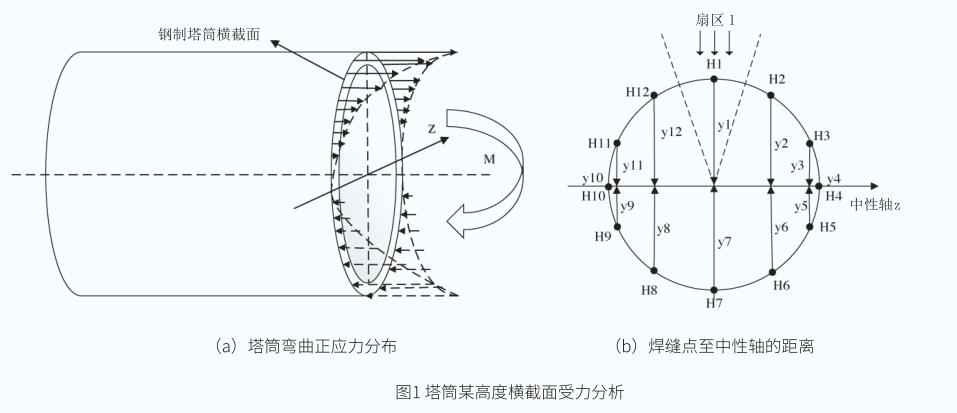


三、疲勞損傷計算
根據扇區湍流強度對風電機組塔筒進行載荷模擬,以塔筒某高度橫截面扇區1內的焊縫點H1為例,在設計壽命期20年內基于扇區載荷的塔筒焊縫疲勞損傷計算流程如下:
根據上述方法對鋼制塔筒不同高度橫截面上的所有焊縫點進行疲勞損傷計算,即可獲得基于扇區載荷的風電機組鋼制塔筒焊縫疲勞損傷結果。
算例分析
以某2.5MW風電機組87m鋼制塔筒為例,進行基于扇區載荷的風電機組塔筒焊縫疲勞損傷計算,該塔筒部分焊接截面幾何參數如表1所示。
該風電機組輪轂中心處的年均風速為7.35m/s,尺度參數和形狀參數分別為6.89和1.96。扇區湍流強度、等效湍流強度和年扇區累積時間分別如圖2和圖3所示。其中,等效湍流強度為考慮12個扇區湍流強度和扇區累積時間等效合成而來。從圖中可以看出,最大和最小湍流強度分別發生在扇區7和扇區2,等效湍流強度介于最大和最小湍流強度之間;最大和次大扇區累積時間分別發生在扇區2和扇區7,即主風向為北偏東,次主導風向為南。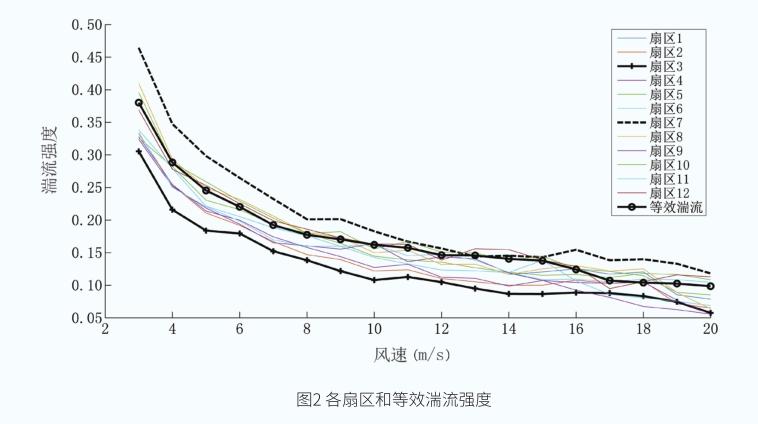
采用上述湍流強度對風電機組塔筒載荷進行模擬,獲得塔筒前后方向彎矩。按照塔筒焊縫疲勞損傷計算流程分別采用扇區和等效湍流強度對塔筒所有高度橫截面上的焊縫點進行疲勞損傷計算,獲得塔筒焊縫疲勞損傷結果,其中塔筒10m、30m、60m和80m高度橫截面上的焊縫點疲勞損傷分布如圖4所示。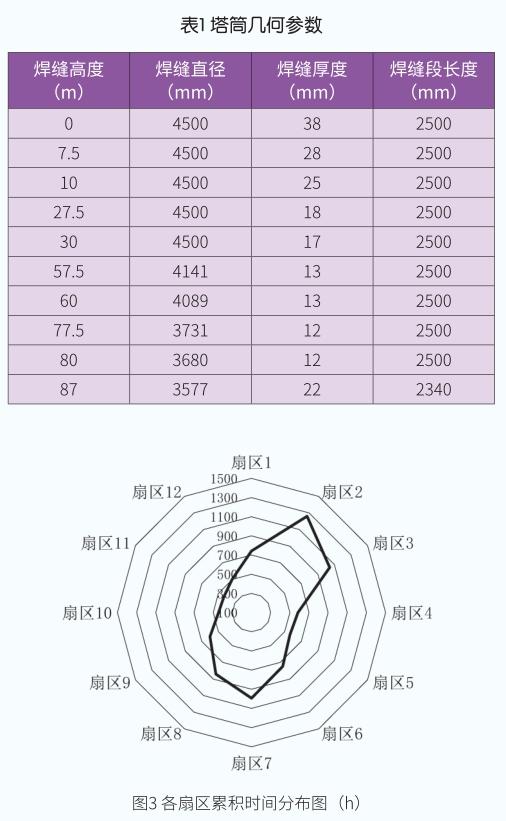
從圖中可以看出,塔筒各截面焊縫疲勞損傷均小于1,滿足疲勞強度要求。當采用扇區湍流強度時,處于塔筒相同橫截面上的焊縫點疲勞損傷不同,4個截面的最大疲勞損傷均發生在扇區7的H7焊縫點,疲勞損傷分別為0.4843、0.8912、0.5843和0.8075;當采用等效湍流強度時,由于塔筒對稱性,處于塔筒相同截面上的不同焊縫點疲勞損傷相同,分別為0.5289、0.9335、0.6143和0.8468,比采用扇區湍流強度時分別增加9.2%、4.7%、5.1%和4.9%。由此可以看出,若采用等效湍流強度對塔筒焊縫進行疲勞強度評估,會高估塔筒焊縫的疲勞損傷。此外,選取的塔筒截面的扇區疲勞損傷分布趨勢與扇區湍流強度和扇區累積時間大小呈現較高的相關性,扇區湍流強度直接影響塔筒扇區載荷大小,扇區累積時間直接影響風速發生的概率,因此,扇區載荷受扇區湍流強度和扇區累積時間的影響較大。由于扇區7的湍流強度最大,扇區累積小時數也較高,焊縫疲勞損傷最大點均發生在扇區7的H7點;雖然扇區2的湍流強度最小,但由于扇區2的累積小時數最大,焊縫點H2的疲勞損傷較大。因此,塔筒相同截面上不同焊縫點的疲勞損傷受扇區載荷的影響較大。
總結
本文在推導風電機組扇區和等效湍流強度之間的關系,以及塔筒相同高度橫截面上不同焊縫點彎曲正應力計算方法的基礎上,采用雨流計數法和疲勞損傷疊加原理獲得了基于扇區載荷的塔筒焊縫疲勞損傷計算方法。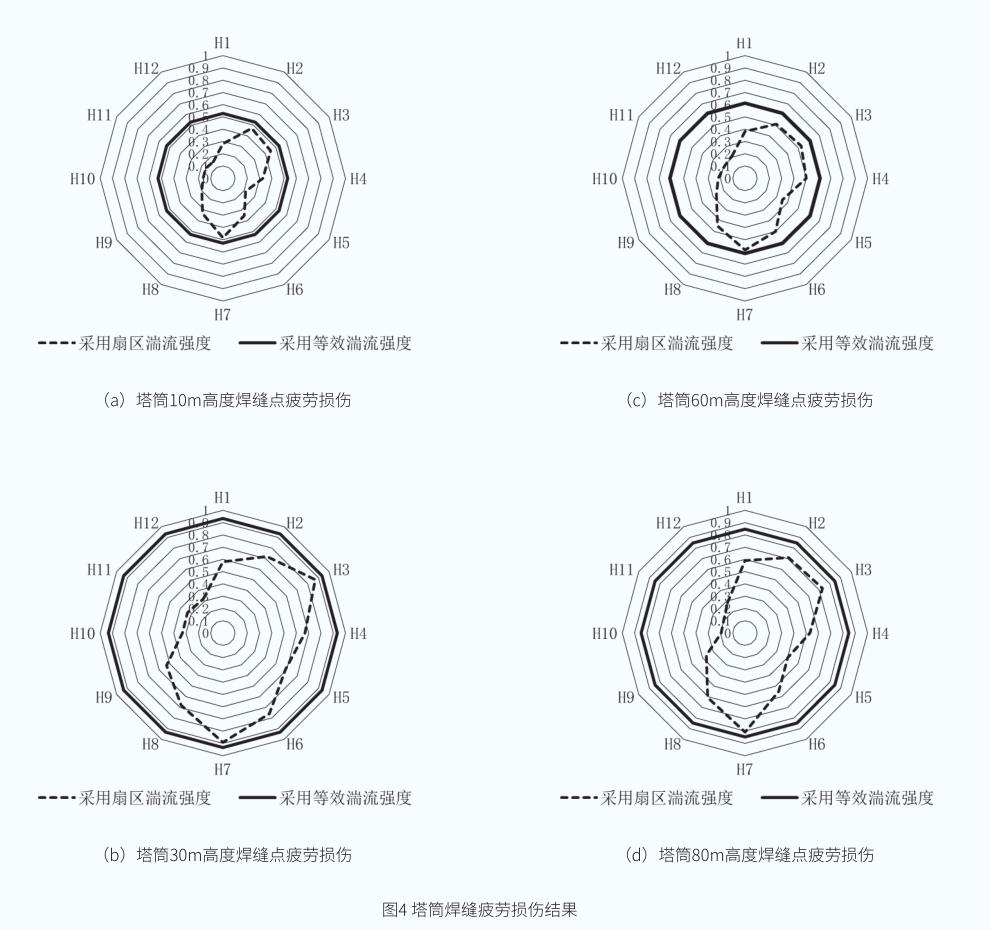
風電機組塔筒截面的扇區疲勞損傷分布趨勢與扇區湍流強度和扇區累積時間具有一定的相關性,若采用等效湍流強度對塔筒焊縫進行疲勞強度評估,會高估塔筒焊縫的疲勞損傷。因此,為了更精細評估風電機組塔筒的安全性,需要考慮不同扇區載荷對塔筒焊縫疲勞強度的影響。
(作者單位:山東中車風電有限公司)

