基于深度強化學習算法的終端區飛機著陸調度算法研究

盧銳軒

（四川大學視覺合成圖像圖形技術國防重點學科實驗室，成都610065）

0 引言

隨著中國空中交通運輸的迅速發展，極速增長的客運、貨運需求和有限的樞紐機場的終端區空域資源的矛盾日益突出，如何解決有限機場終端區里的航班調度問題是整個空中交通問題中的關鍵問題。

航班著陸調度問題（Aircraft Landing Scheduling，ALS）是典型的多目標優化問題，而且是多目標多約束的組合優化問題，航空界一直以來都在處理這類NP 問題（即多項式復雜程度的非確定性問題），目前尚未得出較為完善合理的解決方法，因此在這個問題存在很多研究的空間。目前中國飛機的終端區調度一般采取先來先服務（First-Come, First-Served，FCFS）的方式，這樣比較穩定，計算也比較方便。近年來一直有很多專家學者在將相關智能優化算法應用到航班著陸調度應用領域，如有針對蟻群算法對飛機著陸調度的基于均衡更新蟻群算法的飛機排序調度[1]，也有基于改進免疫粒子群算法的調度算法[2]，其次還有基于遺傳算法的著陸調度問題研究[3]。

深度強化學習算法是一種可以模擬人類學習過程的新型智能算法，其中強化學習算法通過提供一個可反復訓練的環境給待訓練模型，就好比提供一個學習環境給一個孩子，讓他在環境中通過自學來提升自己的能力；而將深度學習的加入則提高了智能體的表達和理解環境的能力，因為環境可能會比較復雜，包含多維信息，利用傳統的強化學習算法來通過表格理解環境已經不太現實。目前有很多學者和科學家在將深度強化學習應用到很多工業領域，如在移動機器人避障領域的研究[4]，還有在自動駕駛方面的應用[5]，也有在行人和車輛檢測方向的研究[6]。ALS 問題中尋求最優解過程就是一種不斷訓練，不斷探索，尋求最優解的過程，可以通過深度強化學習算法來去尋求最優解。

本文分析了航班著陸調度問題的問題來源和流程，建立了用來深度強化學習訓練的航班著陸調度環境，通過引入深度強化學習算法，提出了一系列利用深度強化學習算法來解決航班著陸調度的新方法。通過實驗表明，其算法相對于傳統粒子群算法效果更好。

1 問題描述與建模

1.1 問題描述

本文采用類似滑動窗口的方式對待航班著陸問題，即在一個時間段內，只考慮固定數量的飛機，對該時間段飛機進行安全著陸后，再將時間窗口向后滑動，并對后面的飛機進行處理。一段時間內的一組飛機P={a1,a2,a3,...,an}中的每架飛機包含飛機的機型PT、最佳著陸時間MF、最早著陸時間ME、最遲著陸時間ML、實際著陸時間AL 等主要屬性。

其中飛機類型包括三種：輕H、中L、重S，不同的類型的飛機的提前著陸單位時間成本和延誤著陸單位時間成本，同時不同類型的飛機準備要著陸時與之前剛著陸的飛機的最小安全時間間隔不同；實際著陸時間需要滿足飛機之間的最小安全時間間隔，同時還需要做到使得幾架飛機的總著陸成本盡量小。具體著陸時間與費用的關系如下圖1 所示，其中費用與著陸時間為線性關系，其中飛機延誤相當于飛機需要在機場附近上空盤旋等待降落，提前著陸相當于飛機需要在整個航行過程中進行一定加速飛機，所以延誤著陸單位時間成本會比提前著陸單位時間成本高。

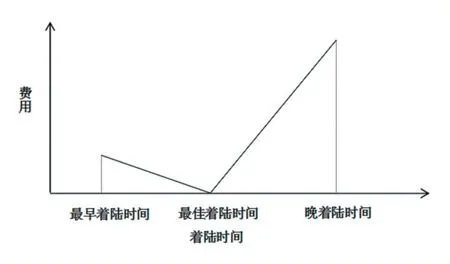
圖1 著陸時間與費用關系圖

1.2 優化目標

假設在某時間段內有n 架飛機需要著陸，如上所述，每架飛機都包含以下屬性：飛機的機型PT、最佳著陸時間MF、最早著陸時間ME、最遲著陸時間ML、實際著陸時間AL，著陸總成本的計算方法為：每架飛機實際著陸時間AL 與最佳著陸時間MF 的差與單位時間提前著陸成本EC 或單位時間延誤著陸成本LC 的乘積和。計算公式：

其中i 表示各架提前著陸的飛機序號，j 表示各架延誤著陸飛機序號，時間的單位是分鐘（min），成本的單位是元每分鐘（￥/min）。

1.3 環境建模

要想將深度強化學習算法應用到航班著陸調度問題中，首先要建立一個能夠讓深度強化學習智能體在其中訓練的環境，這個環境需要做到支持環境與智能體之間的互相交互，如圖2 所示。

圖2 深度強化學習方法

環境中輸出用于表示狀態的state 的包括的信息如表1 所示。

表1 狀態信息表

環境中接收用于表示動作的action 包括的信息如表2 所示。

表2 動作信息表

其中DQN 網絡訓練中使用的是飛機著陸序號來進行著陸，DDPG 網絡中使用的是飛機著陸時間比例進行著陸。

除此之外，環境還需要對神經網絡輸出的動作進行評價和打分，評價的依據就是以計算后著陸時間進行著陸后的總著陸成本，著陸成本越大說明動作方案還不夠合理，這樣得到的動作評價越低，相反著陸成本越低則說明動作方案比較合理，這樣得到的動作評價越高。其中著陸成本取決于飛機著陸時間和最佳著陸時間的差和延誤著陸或提前著陸成本單位時間系數，不同的飛機的著陸成本單位時間系數如表3 所示，單位為元每分鐘。

表3 單位時間成本表

著陸成本的具體計算方法為每架飛機實際著陸時間AL 與最佳著陸時間MF 的差與提前著陸成本EC 或延誤著陸成本LC 的乘積和。計算公式：

其中i 表示各架提前著陸的飛機序號，j 表示各架延誤著陸飛機序號，時間的單位是分鐘（min），成本的單位是元每分鐘（￥/min）。

2 算法設計

2.1 深度強化學習算法

深度強化學習算法中分為基于值函數的方法和基于策略函數的方法，兩種方法的區別就在于基于值函數的深度強化學習方法是用深度網絡去逼近動作的獎勵價值函數，而基于策略函數的深度強化學習方法是用深度網絡去逼近策略函數。因此，兩種深度強化學習方法的深度神經網絡的輸出是不同的，在基于值函數的深度強化學習方法中，深度網絡輸出當前狀態下每個動作的動作價值大小，并由此選擇動作價值最大的動作去執行；基于策略函數的深度強化學習方法中，不再用深度網絡去輸出每個動作的價值函數，而是輸出一個具體動作值，這個動作值可以是連續的，而基于值函數的方法中最終輸出的只能是離散的動作。

DQN 又稱深度Q 網絡，是基于值的深度強化學習算法，也是一種Q 學習與深度學習結合的創新應用，Q學習中是使用Q 表格來記錄狀態-動作對的值的，在DQN 算法中使用神經網絡來擬合Q 函數用來代表動作價值函數。同時，DQN 還具有兩大利器，其一就是使用經驗池的方法來解決相關性以及非靜態分布問題，其二就是使用一個主網絡來生成當前Q 值，再使用目標網絡生成目標Q 值，經過一定次數的迭代將主網絡的參數賦值給目標網絡，兩個網絡不同步更新，提高了訓練的穩定性并且加速了收斂速度。將DQN 應用到飛機著陸算法的過程中，可以通過DQN 輸出飛機的排序序號，為飛機著陸時間定好初始值，再通過粒子群算法對著陸時間進行調優。

DDPG 是基于策略的深度強化學習算法，在動作輸出方面他采用一個網絡來擬合策略函數，直接輸出動作，可以應對連續動作的輸出，在應用到飛機著陸調度中時，可以將動作空間定為[0.0,1.0]區間，代表實際著陸時間在最早著陸時間和最遲著陸時間的比例，通過該方法可以計算出具體的著陸時間。

2.2 粒子群算法

粒子群優化算法（PSO）是由Kennedy 和Eberhart在1995 年提出的群體演化算法，是通過模擬鳥群捕食行為設計的。PSO 算法中首先初始化一波粒子群，其中每顆粒子代表著每個初始化的解，每顆粒子通過不斷探索和信息交互來向最優解靠近，最終每顆粒子都能聚集在最優解的周圍。

將粒子群算法應用在飛機著陸問題中時，每個粒子的位置向量就代表著每架飛機的具體著陸時間，粒子群算法可以把飛機著陸成本當做每個粒子的個體值的評價標準，并讓粒子群不斷向著陸成本更低的方向移動。但在將傳統粒子群算法應用到飛機著陸調度問題中的時候，在面對優化難度較大的問題時，粒子群算法很容易陷入局部最優解，由局部最優解再向全局最優解探索的過程會消耗更大計算時間，由此本文引入了深度強化學習算法來先為粒子群算法制定好初始解，先通過深度強化學習算法的探索能力和學習能力來對最優解進行探索，但深度強化學習算法得出的解可能不夠精確，所以可以再借助粒子群算法進行調優處理。

3 實驗過程及結論

3.1 實驗過程

本文在CPU 為1.7GHz，內存為4GB 的計算機及Windows 7 環境下，采用Python 編程運行上述算法。算法參數如下：仿真實例共4 架飛機，即每次一共為4架飛機進行著陸調度，每架飛機的最佳著陸時間都集中在隨機的3 分鐘范圍內，以保證飛機無法都按照最佳時間進行著陸，即飛機需要進行著陸時間的調整。總共包含兩次實驗：

實驗一：將DDPG 應用到飛機著陸調度問題中，首先將DDPG 的輸出的動作action 的范圍調整為[0,1]，假設輸出的動作為a，待調整飛機的最早著陸時間為me，最遲著陸時間為ml，則計算出的實際著陸時間為me+a*（ml-me），然后將幾架飛機的著陸時間按順序排列，如果后著陸的飛機不滿足最小安全時間間隔原則，則將后著陸飛機以此向后延誤，進過調整后得到最終飛機實際著陸時間。作為對比的算法為先來先服務算法（FCFS），即讓飛機按照到達機場的順序進行以此著陸，如果飛機不滿足最小安全時間間隔則直接按著陸順序向后延遲。實驗結果如下圖3 所示，其中實驗數據取沒100 次試驗的平均值，橫軸代表實驗次數，單位為每100 次，縱軸為著陸成本，單位為元。

圖3 實驗一

實驗二：將DQN 結合粒子群算法應用到飛機著陸調度中，首先在DQN 的每步動作中，讓動作網絡輸出的不是具體著陸時間而是著陸順序，現根據飛機的先后順序，依次為飛機計算著陸時間，而不是按照初始的先后順序來計算著陸時間。計算好的時間作為初始化時間再利用粒子群算法進行微調和優化，從而計算出確切的著陸時間。對照實驗依然為先來先服務（FCFS），實驗結果如下所示，其中實驗數據取沒100 次試驗的平均值，橫軸代表實驗次數，單位為每100 次，縱軸為著陸成本，單位為元。

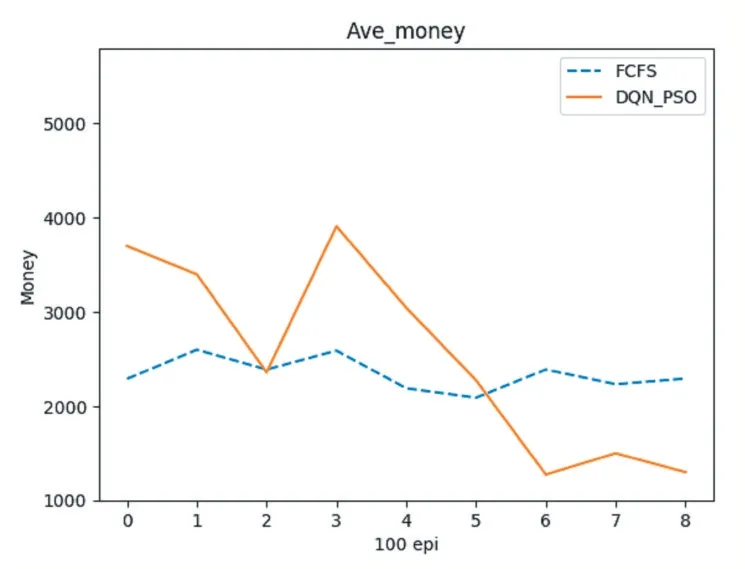
圖4 實驗二

3.2 實驗結論

通過以上實驗的對照，可以發現經過一段時間的訓練，兩種深度強化學習算法在飛機著陸調度的應用結果都好于現在主流的先來先服務FCFS 算法，同時經過粒子群算法優化的實驗二的數據要更好一些。在將粒子群算法與深度強化學習DQN 算法結合來解決飛機著陸調度問題中時，將深度強化學習這種反復訓練不斷逐優的特性和超強的學習能力加入飛機著陸調度過程，提升了粒子群算法的探索能力并且解決了直接將深度強化學習算法應用到飛機著陸調度算法中時，最終計算結果優化不夠的問題。同時將深度強化學習算法與群計算智能算法結合的這種思路也為避免深度強化學習算法和群智能算法陷入最優解提供了新的解決方案。