海洋平臺升降裝置的齒輪齒條均載特性研究

陳寶慶，葉福民，孟淼

(江蘇科技大學 機械工程學院,江蘇 鎮江212003)

0 引言

自升式海洋平臺具有造價低、定位能力強、同步性好和用鋼量少等優點，被廣泛運用于海洋石油的開發和勘探工程[1]。齒輪齒條升降系統是自升式海洋平臺的核心裝置之一，其原理是通過一系列的減速變速過程，最終通過兩個小齒輪與作為樁腿齒條的異側嚙合來提升平臺。在理想狀態下，齒條兩側的小齒輪受力是相等的。但是由于升降裝置的振動、齒輪嚙合誤差等因素的影響，齒條和兩側小齒輪的嚙合力存在一定的偏差，結果會造成升降裝置載荷分布不均勻，即不均載的現象。這將會使平臺產生振動、噪聲，輪齒出現點蝕，甚至導致輪齒折斷。

國內外學者針對齒輪的均載特性做了大量的研究，且現有的關于齒輪均載性能的研究，大都是針對行星輪系的均載性能研究。KAHRAMAN[2]建立了單級行星輪系的集中參數模型，并討論了系統的固有特性。BODAS[3]等分析了載荷和輪齒制造誤差對行星傳動均載特性的影響; SINGH[4]等通過實驗詳細研究了行星傳動系統中的載荷不均等特性;陸俊華[5]等人從動力學角度建立2K-H型行星傳動系統的計算模型，研究了太陽輪浮動、裝配和安裝誤差以及轉速等因素對系統均載特性的影響。孫智民[6]等建立了行星齒輪傳動系統非線性動力學模型，分析了齒輪副的綜合誤差和齒側間隙對均載性能的影響; 方宗德[7]等得到了2K-H行星減速傳動系統的時域和頻域解，分析了各行星輪上的均載特性和輪齒偏心誤差對其均載特性的影響;葉福民[8]等人建立了非等模數、非等壓力角NGW 型行星齒輪系的計算模型，并通過建立方程，用理論推導的方式討論了壓力角、齒輪誤差、嚙合剛度等對系統的均載特性的影響。其他學者[9-10]也對多級行星齒輪傳動系統的均載特性做了研究。

本文以自升式海洋平臺齒輪齒條升降裝置的樁腿為研究對象，分別從升降裝置在載荷、壓力角以及模數變化情況下，對齒輪齒條升降裝置進行動力學研究，揭示升降載荷、壓力角和模數對于均載系數變化的影響，可以為升降裝置的設計優化提供理論參考，也可以為自升式海洋平臺齒輪齒條升降裝置動力學分析提供理論參考。

1 齒輪齒條升降裝置的均載機構及系統的主要參數

圖1為自升式海洋平臺升降系統的示意圖。電動機提供的動力傳遞給行星減速器的“中心太陽輪”，然后由行星架10和外齒輪1分別在左右兩軸主動輸出。2個主動七齒小齒輪構成一個“統一輸出”的差動輪系，即2個左右七齒小齒輪的模數相同、轉速相等。

升降平臺在上下運動的過程中，小齒輪要承擔平臺的重力。在正常的工況下，每個升降單元的承載能力不能低于400t，所以每個小齒輪的承載能力為200t[11]。此升降裝置是由6個小齒輪與一條齒條組成，因此給齒條質心加一個12000kN的力來模擬升降平臺的載荷，研究對象是每根樁腿的升降裝置的一組升降單元中的七齒小齒輪。表1為升降裝置各部件參數。

1—外齒輪；2—七齒齒輪；3—齒條；4—七齒齒輪；5—帶外圈的內齒圈；6—行星輪；7—太陽輪；8—惰輪；9—系桿；10—行星架。圖1 海洋平臺齒輪齒條式升降裝置示意圖

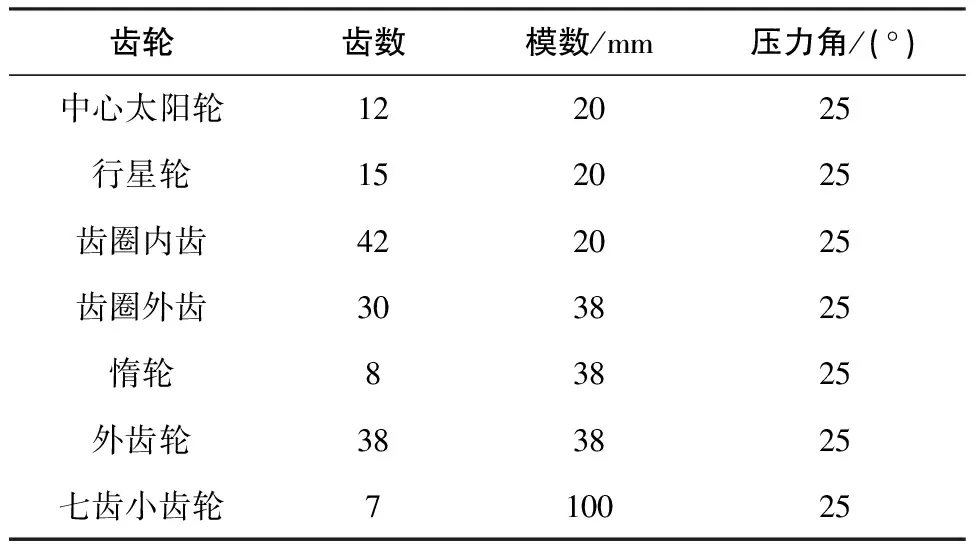
表1 升降裝置各個部件參數

2 齒輪齒條升降裝置動力學模型的建立

a) 升降裝置的動力學模型

首先在Pro/E中建立升降裝置的三維模型，接著在Pro/E中轉換成Parasolid 格式中性文件，然后在ADAMS軟件中導入中性文件，并對各個部件施加相應的約束、創建接觸力并設置相應的參數，施加驅動。

b) 升降裝置動力學模型的參數設置

1)約束的設置

與大地間建立旋轉副的齒輪有：太陽輪、行星輪、小齒輪、外齒輪、齒圈，旋轉中心為各自的質心；其中3個行星齒輪與大地之間建立旋轉副時，小齒輪為參照物；齒條與大地之間建立移動副。

2) 接觸力中參數的設置

接觸剛度為2個物體接觸時表面抵抗彈性變形的能力。根據赫茲理論，接觸剛度系數計算如下：

(1)

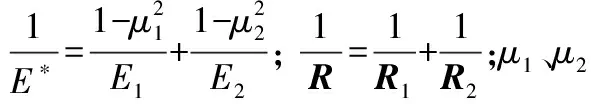
代入數據，得到剛度系數為3.98×106N/mm2。

3) 模型驅動的設置

由于太陽輪為輸入動力的一端，因此給太陽輪施加驅動。設置轉速為180°/s(30r/min)。求解器的仿真時間設置為t=20s，仿真步數stepsize=100。

c) 升降裝置的動力學計算結果

當裝置在正常升降時，平臺承受的設計升降載荷為12000kN。得到齒輪齒條接觸力曲線圖，如圖2所示。當小齒輪的升降載荷為12000kN時，每個小齒輪受到的切向力理論值FX為2000kN，那么小齒輪受到的接觸力的理論值F0為:

(2)

式中：α為壓力角，?=25°，經過計算F0約為2200kN。

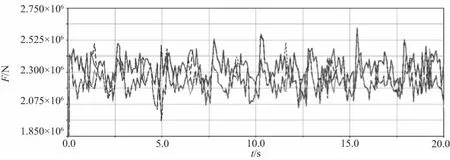
圖2 載荷為12000kN時的接觸力曲線圖

3 參數影響分析

3.1 齒輪齒條升降裝置的均載定義與計算

通過ADAMS進行仿真分析，在后處理中得到接觸力的數值，導入到Excel中進行數據處理，再將數據導入到MATLAB中進行數據處理，得到均載系數隨著升降載荷、小齒輪壓力角、模數變化的曲線圖。圖3為齒輪齒條示意圖，假設小齒輪1受到的載荷值為F1，小齒輪2受到的載荷值為F2，設小齒輪1和2受到載荷的理論值為F，設均載系數為β，小齒輪的均載系數為：

(3)

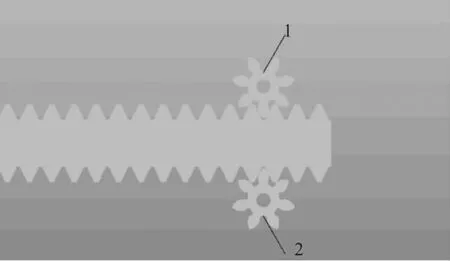
圖3 齒輪齒條示意圖

在ADAMS的PostProcessor模塊中，得到仿真后曲線的參數，通過處理將數據導入到表格中，在表格中進行數值運算。由于齒條同一側有3個小齒輪，所以每組只要測量1個，本文取后處理中的contact1和contact4曲線。通過Excel中的數值運算，得到均載系數，最后在MATLAB中繪制均載系數曲線。

由于最終得到的均載系數是一條曲線，為了便于比較，所以取曲線上最大值點作為小齒輪最終的均載系數。

3.2 載荷對于均載系數的影響

采用上述方法分別計算升降平臺在載荷分別為18000kN、24000kN、30000kN，36000kN時的均載系數。在MATLAB中，通過輸入代碼得到曲線圖，得到在不同升降載荷下，均載系數隨著時間的變化曲線圖一，如圖4所示，同時得到均載系數隨著載荷變化的曲線，如圖5所示。

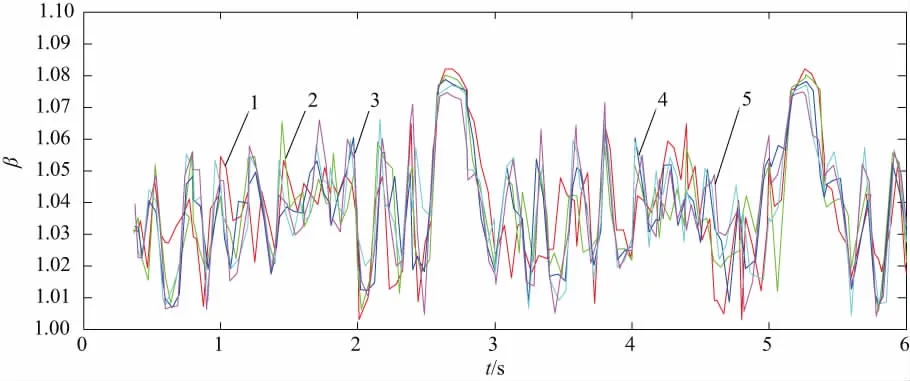
曲線1—載荷為12 000 kN時；曲線2—載荷為18 000 kN時； 曲線3—載荷為24 000 kN時；曲線4—載荷為30 000 kN時；曲線5—載荷為36 000 kN時 。圖4 均載系數隨著時間的變化曲線圖一

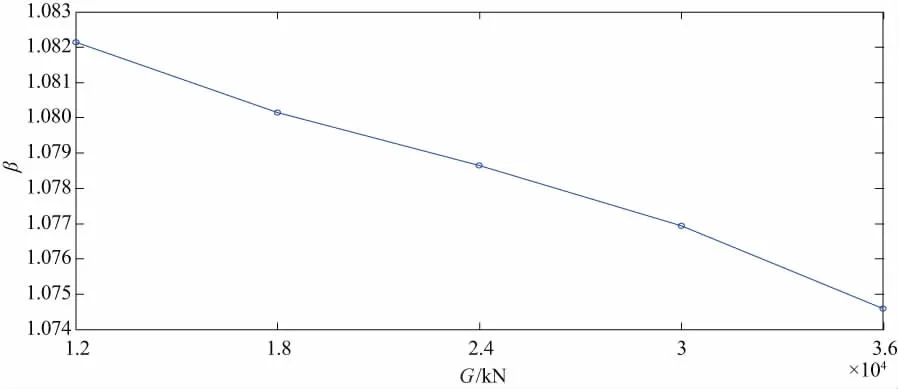
圖5 均載系數隨著載荷的變化曲線圖

由圖5可知，曲線有周期性的變化，周期大約為2.5s，這說明小齒輪轉過一個齒大約需要2.5s。從圖5中還可以發現齒輪發生了單雙齒交替時，均載系數是明顯變化的，雙齒嚙合的時候，均載系數大；單齒嚙合的時候，均載系數小。由圖6可以看出，小齒輪的載荷在增大的情況下，小齒輪的均載系數呈現出變小的趨勢，均載系數的值大致在1.074～1.082之間變化。

3.3 小齒輪壓力角對于均載系數的影響

分別計算小齒輪在壓力角為25°、26°、27°、28°、29°時小齒輪的均載系數，得到在不同壓力角下，均載系數隨著時間的變化曲線圖二，如圖6所示，同時得到均載系數隨著壓力角變化的曲線，如圖7所示。

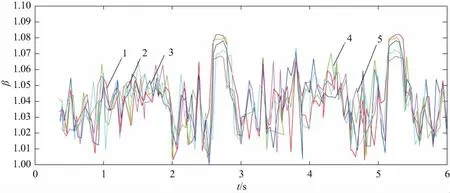
曲線1—壓力角為25°時；曲線2—壓力角為26°時；曲線3—壓力角為27°時；曲線4—壓力角為28°時；曲線5—壓力角為29°時。圖6 均載系數隨著時間的變化曲線圖二

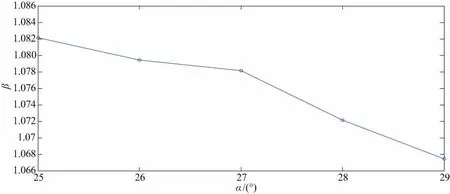
圖7 均載系數隨著壓力角的變化曲線圖

由圖6可知，曲線有周期性的變化，周期大約為2.5s。這說明小齒輪轉過一個齒大約需要2.5s。從圖中可以看出，齒輪在運動過程中，均載系數是不斷變化的，雙齒嚙合的時候，均載系數大；單齒嚙合的時候，均載系數小。由圖7可知，小齒輪在壓力角變化的情況下，小齒輪的均載系數大致在1.067～1.082之間變化，而且隨著小齒輪壓力角變大，均載系數呈現變小的趨勢。

3.4 小齒輪模數對于均載系數的影響

分別計算小齒輪的模數為90mm、95mm、100mm、105mm、110mm時小齒輪的均載系數，得到在不同模數下，均載系數隨著時間的變化曲線圖三，如圖8所示，同時得到均載系數隨著模數變化的曲線，如圖9所示。

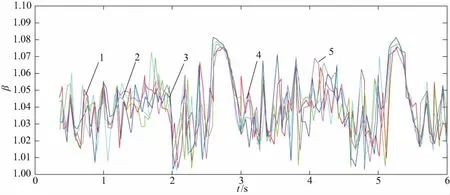
曲線1—小齒輪模數為90 mm時；曲線2—小齒輪模數為95 mm；曲線3—小齒輪模數為100 mm時；曲線4—小齒輪模數為105 mm時；曲線5—小齒輪模數為110 mm時。圖8 均載系數隨著時間的變化曲線圖三

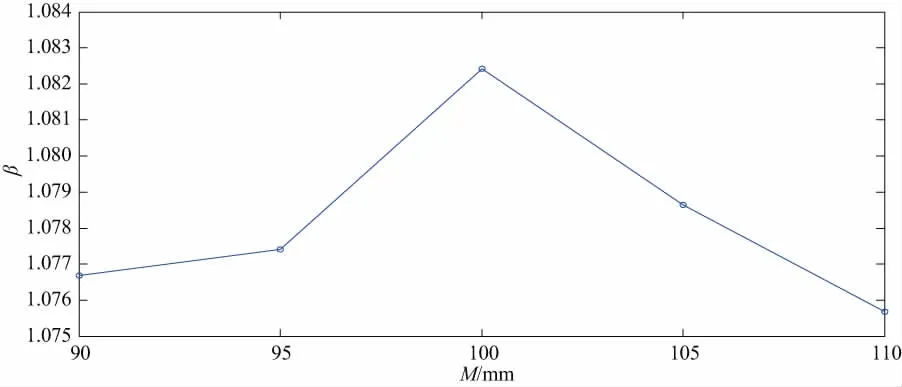
圖9 均載系數隨著模數的變化曲線圖

由圖9可知，曲線有周期性的變化，周期大約為2.5s，這說明小齒輪轉過一個齒大約需要2.5s。由圖10可知，當小齒輪模數由90mm變化到110mm時，小齒輪的均載系數呈現先增加后減小的趨勢，即小齒輪的模數在從90mm增加到100mm的過程中，均載系數是變大的，而小齒輪的模數在由100mm增加到110mm的過程中的時候，小齒輪的均載系數呈現變小的趨勢。

4 結語

對自升式海洋平臺升降裝置齒輪齒條進行了動力學分析并研究了小齒輪的均載系數隨著載荷、壓力角、模數變化的變化情況后，對各種情況的變化規律總結如下：

1) 在小齒輪的載荷由12000kN增加到36000kN的過程中，隨著升降載荷的變大，小齒輪的均載系數有變小的趨勢，均載系數在1.074～1.082之間變化。因此升降系統噸位越大，升降平臺運行越穩定。

2) 在小齒輪壓力角由25°變化到29°的過程中，隨著小齒輪壓力角的變大，小齒輪的均載系數有變小的趨勢，均載系數在1.067～1.082之間變化。因此在可供選擇的壓力角范圍內，選擇較大的壓力角。

3) 在小齒輪模數由90mm增加到110mm的過程中，隨著小齒輪模數的變大，均載系數呈現出先增大然后減小的趨勢。總體來說，模數對于小齒輪的均載性能影響不大。