基于Linux的開放式數控系統加工軌跡仿真功能研發

陳平斌，林述溫，陳坤火

(福州大學 機械工程及自動化學院，福建 福州 350116)

0 引言

開放式數控系統，其結構開放、模塊具有互換性，功能可擴展，已成為數控技術發展的趨勢[1]。數控系統的加工仿真功能可有效檢驗NC代碼的正確性、檢驗加工程序是否存在過切或欠切，優化切削參數[2-3]等。大多數控系統仿真功能需要借助CAM軟件實現，如UG、CATIA等。隨著計算機建模技術的發展，許多學者對數控仿真系統進行了研究，如文獻[4] 運用實體幾何法建模思想研究了數控車床運動仿真及切削仿真；文獻[5] 采用Z-MAP方法對數控銑削加工仿真進行了研究；文獻[6]基于離散建模對三軸數控銑削加工仿真算法進行研究。但上述研究大都是建立在Window平臺上，而且系統能夠支持仿真的對象有限。智能制造環境下對數控系統提出了開放性、集成CAM軟件，方便編程模擬的需求[6]。為此，本文針對基于Linux平臺，采用PC+可編程I/O卡體系的開放式數控系統[7]，研究了加工軌跡仿真功能單元的通用模型，并基于該模型，研發了數控銑削機床的加工仿真功能。

1 軌跡仿真功能單元通用模型設計

數控系統是一個多任務、高實時的控制系統，基于IEC61499[8]功能塊模型建立軌跡仿真功能單元的標準模型，可以在滿足上述需求的同時降低開發周期。IEC61499基本功能塊模型(BFB)如圖1所示。根據該模型，建立加工軌跡仿真功能單元的通用模型，如圖2所示。功能單元的執行由事件觸發驅動，如開始仿真事件、觸發事件可以多樣，但是接口必須符合BFB模型標準。軌跡仿真控制執行表依據觸發事件切換狀態，并調用此狀態下的控制算法進行處理，如若觸發事件為開始仿真，ECC的狀態由FREE轉為START狀態，開始處理刀位、毛坯等數據，并依次調用相應算法進行加工仿真計算。處理完畢后自動更新內部數據，將得到的數據由數據輸出接口輸出。當ECC的狀態為FINISH狀態，軌跡仿真功能單元執行完畢。

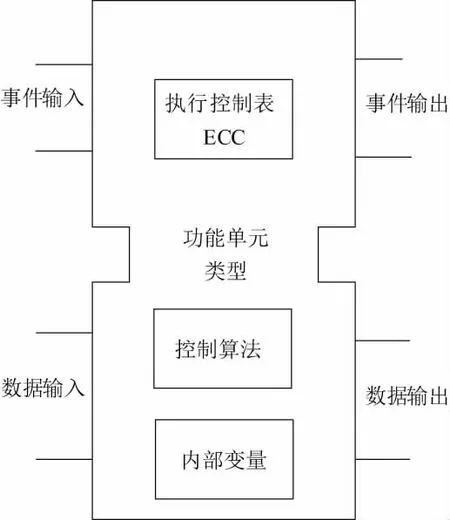
圖1 IEC61499基本功能塊模型

圖2 基于BFB的軌跡仿真功能單元通用模型

2 數控銑削加工仿真功能單元的開發

2.1 改進離散矢量建模原理

在仿真計算中，采用離散矢量建模法進行加工仿真的實質[9]是刀具掃描體與毛坯體求交運算和毛坯體數據的更新顯示。因此，采用何種方式、何種精度離散出用于求交計算的數學模型是該方法的關鍵所在。

均勻網格離散建模，是以一定的網格間距(離散精度)將零件包圍在xoy平面的投影面均勻劃分為有限個網格。每個網格點法矢方向與零件外表面的交點稱為Z-MAP點。均勻網格的離散方式簡單但是其仿真速度和離散精度存在矛盾，要想得到較好的仿真效果，只有不斷地提升劃分精度，但是會帶來大量數據，嚴重影響仿真速度。

針對上述問題，進行了改進和優化，如圖3所示。首先以一般的精度對零件曲面進行均勻離散劃分，在零件外表面曲率值較大處進行局部增加劃分精度，從而提升仿真效果，又兼顧了仿真速度。本文將這種局部優化的方法稱為改進離散矢量建模方法，建立的數學模型稱為非均勻離散方式模型。

圖3 非均勻離散方式模型

2.2 毛坯體的建模

毛坯體建模采用改進離散矢量建模法，以方形塊料為例進行闡述毛坯模型建立的流程如下。

首先定義毛坯和仿真精度，包括毛坯尺寸、加工余量、仿真精度和速度控制。仿真精度和速度用Epsilon參數和Step參數控制。Epsilon表示相鄰均勻離散網格之間的間距，Step用于改變單步的網格數，來調節粗加工和精加工時對網格間距的不同要求。在算法中，兩者之積控制了仿真精度和速度。然后進行均勻離散網格劃分，在毛坯建模中，將Z-MAP點的初始高度值賦值為毛坯高度，均勻離散網格之間的間距根據刀具類型和切削深度進行確定。球型刀和環形刀可按式(1)確定。

(1)

式中:et為切削深度；R為刀具半徑。

對于平底刀

Epsilonmax=2et

(2)

在網格實際劃分時由于切削深度無法精確估計，大多數情況下et遠遠小于R。為了簡化起見，在仿真精度控制中將Epsilon取值范圍定為0.1～1.0mm，并通過Step參數來調節粗加工和精加工時對網格間距的不同要求。實際采用的網格劃分間距L為兩者之積。

L=Epsilon×Step

(3)

在均勻離散網格劃分完成后，對零件表面曲率較大之處添加非均勻離散網格點。非均勻離散網格劃分流程如圖4所示。先將加工零件曲面離散為四邊面片拼接表示，然后進行曲率估算。顯然曲率較大之處四邊面片不同方向兩弧長之積將越大。據此通過遍歷所有四邊面片，計算其兩弧長之積Si并和曲率較小處四邊面片S0相比較來確定是否需要添加非均勻離散網格點。在算法中，令S0=L×L，并設定當Si>1.5S0時，以等間距在均勻離散網格基礎上添加非均勻離散網格點。

圖4 毛坯體局部非均勻離散網格劃分流程

2.3 刀具掃描體與毛坯模型交點計算

刀具在本仿真建模中可視作剛體處理，其模型建立后就保持不變。因此，關鍵是刀具掃描體與毛坯模型求交計算后模型的更新顯示。所謂刀具掃描體是指刀具在刀位點之間移動形成的包絡體，不同刀具類型會形成不同的包絡體，因此涉及的求交計算也不同。

毛坯體數據的更新依賴于離散點法線方向與刀具掃描體的求交計算，為了簡化計算和加快仿真速度，本文在每一個刀位點，先得到切削加工影響的局部區域(刀具在xoy平面投影的外切最小正四邊形)，在此區域進行求交計算，達到毛坯數據的局部更新。

1) 離散點法矢與球形刀掃描體交點位置計算

球形刀的求交計算如圖5所示，設刀具(半徑為R)從一個刀位點(xs,ys,zs)移動到另一刀位點(xe,ye,ze)，兩點的連線d稱為刀具運動的中心線，其在xoy平面的投影線記作dxy，刀心在xoy平面的投影點記作點s和點e。p(xp,yp)為xoy平面局部區域的一離散點，其法矢方向直線與球形刀具掃描體的交點為p′(xp,yp,zp)，此時對應的刀心坐標為(xc,yc,zc)，則：

(4)

(5)

式中:Δx=xe-xs；Δy=ye-ys；Δz=ze-zs。

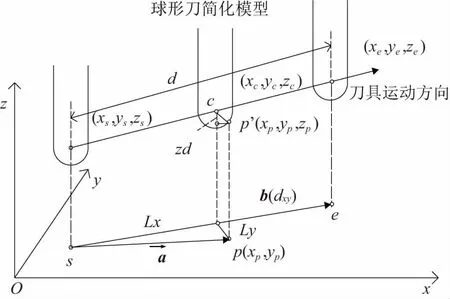
圖5 球形刀與毛坯交點的幾何關系示意圖

連接點s和點p得到有向線段記作向量a，連接點s和點e得到有向線段(長度為dxy)記作向量b。記向量a在dxy的投影長度為Lx，在dxy垂線上的投影長度為Ly，由向量投影原理和幾何關系可得：

(6)

(7)

(8)

設過當前位置刀心點c(xc,yc,zc)在加工影響的局部區域取離散網格點p(xp,yp)，作垂直于dxy線段的平面與球形刀相交得到一半圓弧，該半圓弧即為當前刀具的切削刃。由包絡線的特性，半圓弧上的點與刀具中心線的距離為Ly，則交點p′(xp,yp,zp)與當前位置刀心點(xc,yc,zc)在z軸方向的距離zd為

(9)

由此可得離散網格點與球形刀具掃描體交點處的高度值zp：

(10)

2) 離散點法矢與環形刀掃描體交點位置計算

環形刀的切削刃為圓環面下部外側面。設刀具半徑為R，切削刃半徑為r，對于平底刀可以看做是環形刀的特例(切削刃半徑r為0)。環形刀在兩刀位運動之間的某一位置如圖6所示。p′(xp,yp,zp)為加工影響的局部區域一離散網格點p與環形刀具掃描體的交點，其與當前位置刀心點Oc(xc,yc,zc)在z軸方向的距離為zd。以dxy方向為x軸，z軸方向不變，建立一個新的坐標系。α1是p′o′連線與z軸方向的夾角，α2是xoy平面pc與x軸方向的夾角。

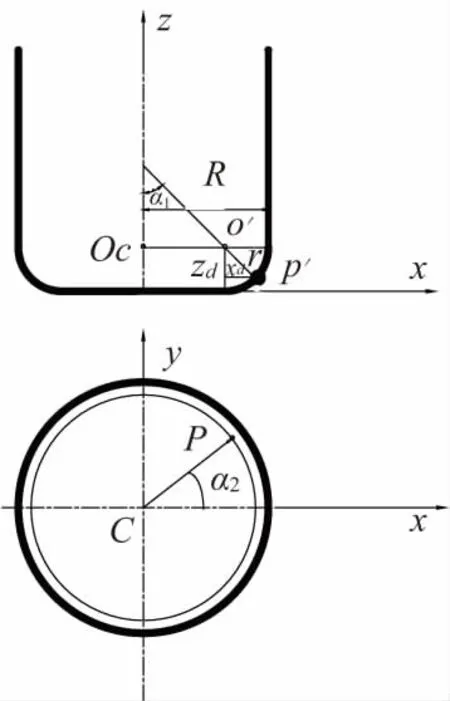
圖6 環形刀求交計算

由包絡體特性可知，點p′的法線(p′o′)方向與刀具速度方向正交，設刀具速度方向T，p′的法線方向為N，則有：

T·N=0

T可取為刀具中心點移動方向，N取為單位法線方向則：

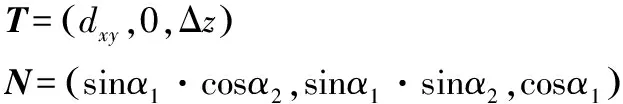
由幾何關系可知：

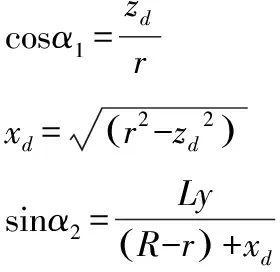
將式(12)、式(13)代入式(11)可得

(14)

在算法中采用迭代法求解zd，根據式(8)求得zc，則離散網格點與環型刀具掃描體交點處的高度值zp：

zp=zc-zd

(15)

毛坯體數據的更新算法流程如圖7，其基本原理是通過比較求交計算所得zp值，當新zp小于原zp值時更新離散點的z值，否則保留原值不變。當遍歷完當前刀位點局部區域的所有離散網格點后，調用Open GL庫glBegin(GL_QUAD_STRIP) 函數繪制四邊面片拼接形成切削后的毛坯外形。

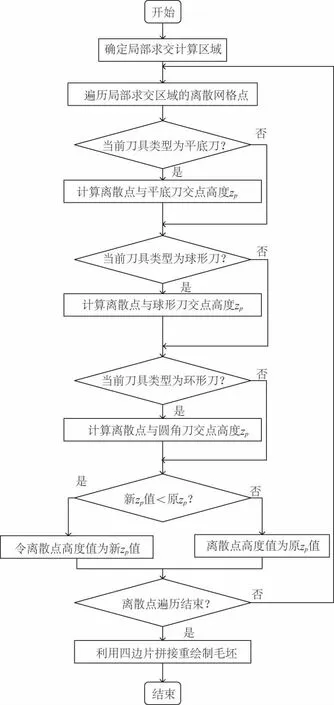
圖7 毛坯體數據更新算法流程

所研發數控銑削加工軌跡仿真功能單元的運行流程如圖8，在外部輸入事件的驅動下，通過執行控制表切換狀態進入下一個流程，并調用相應算法實現從毛坯定義、模型離散、求交計算、數據更新繪制等過程。

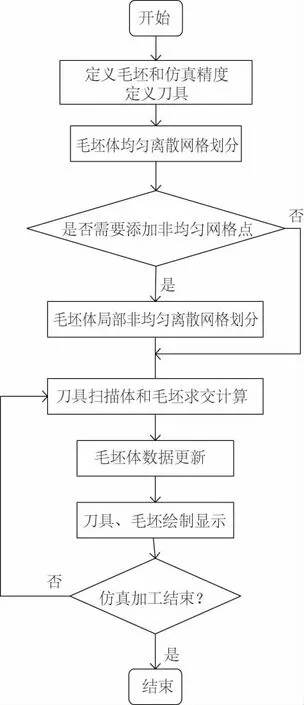
圖8 數控銑削加工軌跡仿真功能單元運行流程

3 數控銑削加工軌跡仿真功能驗證

圖9所示為數控銑削加工仿真功能單元的默認顯示界面。通過打開軌跡文件按鈕。調用數控系統粗插補計算后的刀位文件。刀位文件獲取采用前瞻速度、加速度預處理插補算法，詳見文獻[10] 。仿真時毛坯選為塊料，加工精度控制參數設為Epsilon×Step=0.5×5。采用平底刀和球型刀加工仿真時的效果如圖10所示。此外，仿真功能單元能對過切、欠切進行檢查并輸出錯誤的程序段號。如圖11所示，當發生過切時將進行提示，并在毛坯模型上通過與正常加工時差異化的顏色(圖中為灰色)體現。實際加工試件經測量數據對比發現，仿真結果和實際加工結果基本一致，所研發數控銑削加工仿真功能單元適應本開放式數控系統。

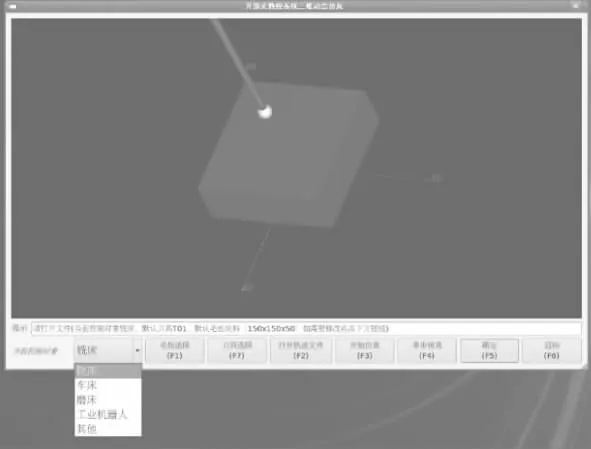
圖9 銑床軌跡仿真功能單元默認顯示界面

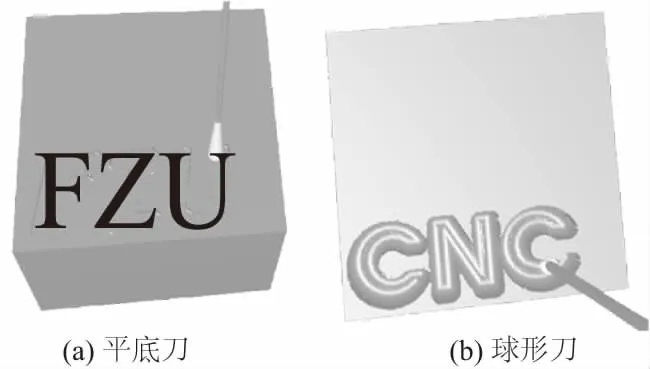
圖10仿真加工結果

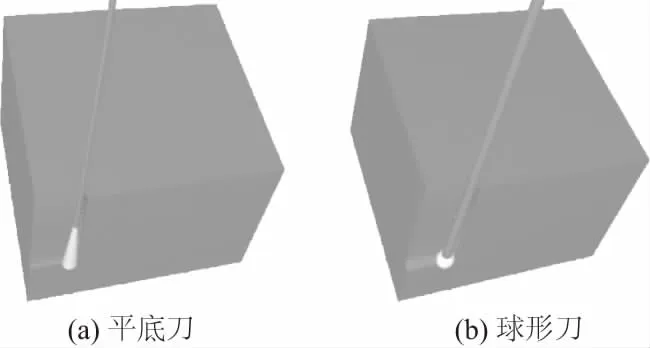
圖11 過切檢查

4 結語

本文針對PC+可編程I/O(接口)體系結構的開放式數控系統，為滿足不同控制對象的仿真需求，基于IEC61499基本功能塊模型設計了適應本開放式數控系統的軌跡仿真功能的通用模型。仿真建模時，為改善毛坯數學模型離散化精度和仿真速度之間存在的矛盾，在均勻網格離散基礎上加以改進，并以數控銑床為例，基于通用模型和改進離散矢量建模法設計開發了三維動態加工仿真功能單元，實現了試切模擬和軌跡錯誤檢查。毛坯建模時，離散化精度和仿真速度之間存在矛盾，本文采用改進離散矢量建模法，使之得到一定改善，但仍有待進一步探索新方法，以提高仿真精度和兼顧速度。