基于改進PSO的局部陰影下光伏陣列MPPT控制

王豪，王宏華

(河海大學(xué) 能源與電氣學(xué)院，江蘇 南京 210098)

0 引言

光伏發(fā)電具有分布廣泛、無污染、方便等優(yōu)點，成為當(dāng)今的研究熱點。其中，光伏系統(tǒng)的最大功率點跟蹤(maximum power point tracking，MPPT)控制，是提高其發(fā)電效率的重要措施之一。然而在局部陰影下，光伏陣列的P-V曲線呈現(xiàn)多峰值現(xiàn)象，傳統(tǒng)的MPPT算法(如爬山法、電導(dǎo)增量法等)難以追蹤到最大功率點。針對該問題，文獻[1] 利用局部陰影下光伏陣列最大功率點電流與短路電流之間近似的比例關(guān)系，提出一種三步驟全局MPPT算法，其結(jié)構(gòu)簡單，但動態(tài)調(diào)整過慢。文獻[2]針對傳統(tǒng)MPPT算法進行改進，提出了差分進化(DE)算法與變步長擾動觀察法結(jié)合的復(fù)合控制算法，但其依賴于光伏組件參數(shù)并且控制復(fù)雜。文獻[3]采用斐波那契(Fibonacci)搜索法，但是該方法不能對任意情況進行MPPT，實用性不強。

粒子群優(yōu)化算法(particle swarm optimization, PSO)作為全局尋優(yōu)算法，非常適用于多峰值光伏系統(tǒng)的MPPT。文獻[4-6] 采用粒子群算法實現(xiàn)多峰MPPT控制，能對任意陰影情況進行最大功率點跟蹤，但其收斂速度慢。文獻[7-8] 對傳統(tǒng)粒子群算法進行改進，分別提出了慣性權(quán)重對數(shù)遞減粒子群和變異粒子群算法，可顯著提高收斂速度，但其仍易陷入局部最優(yōu)。基于此，本文采用改進的粒子群優(yōu)化算法實現(xiàn)光伏陣列局部陰影下MPPT控制，針對傳統(tǒng)PSO容易陷入局部最優(yōu)解，即“早熟”缺陷，引入自適應(yīng)調(diào)節(jié)的慣性權(quán)重和學(xué)習(xí)因子進行進一步優(yōu)化，提高算法的收斂速度。通過仿真驗證改進后的算法在不同陰影條件下，能夠快速且準確地跟蹤最大功率點，提高了光伏陣列輸出效率，具有良好的實用價值。

1 光伏陣列的多峰值特性分析

單塊光伏電池可用圖1的等效電路來表示。

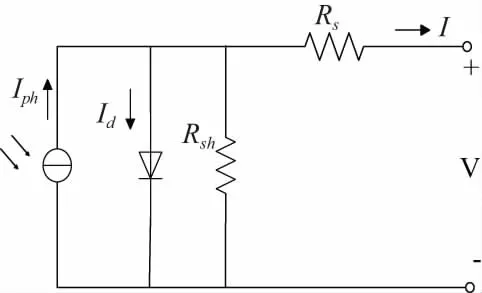
圖1 等效電路圖

本文采用一種適合工程應(yīng)用的近似仿真模型[9-11]，根據(jù)電池廠商提供的標準環(huán)境下相關(guān)參數(shù)和對不同環(huán)境下電池性能參數(shù)的修正得到如下公式：

I=Isc[1-C1(eU/(C2Uoc)-1)]

(1)

C1=(1-Im/Isc)e-Um/(C2Uoc)

(2)

C2=(Um/Uoc-1)[ln(1-Im/Isc)]

(3)

式中：U、I為光伏電池的輸出電壓和電流；Isc為短路電流；Uoc為開路電壓；Im和Um分別為最大功率點所對應(yīng)的電流和電壓。

光伏陣列由多個單體光伏電池串并聯(lián)而成，其輸出特性可視作單體電池輸出特性的疊加。由文獻[1] 可知，局部陰影下并聯(lián)的光伏組件可相對獨立工作，其P-V曲線仍呈單峰特性；然而，處于局部陰影下串聯(lián)的光伏組件，其P-V曲線將呈現(xiàn)多峰值特性。圖2為3個光伏電池串聯(lián)組成的陣列，每個光伏電池并聯(lián)一個旁路二極管，防止其工作在反向電壓。

本文仿真采用的太陽能電池型號為MG-P50，廠家給出的性能參數(shù)為：Pm=50W,Uoc=21.5V,Um=18.4V,Isc=2.95A,Im=2.72A。參考溫度是25℃，參考光照為1000W/m2。在局部陰影下，3塊光伏電池的光照強度將不再相同。假設(shè)此時PV1的光照強度為1000W/m2，PV2為800W/m2，PV3為600W/m2，在該種情況下陣列輸出的P-V、I-V曲線如圖3所示。此時，陣列的開路電壓Uoc_array=64.5V。當(dāng)陣列輸出電流iIsc2>Isc3)，3個旁路二極管都不導(dǎo)通，PV1、PV2、PV3共同輸出功率；當(dāng)Isc3Isc2時，只有PV1輸出功率；因此，陣列的輸出P-V曲線呈現(xiàn)多峰值特性。

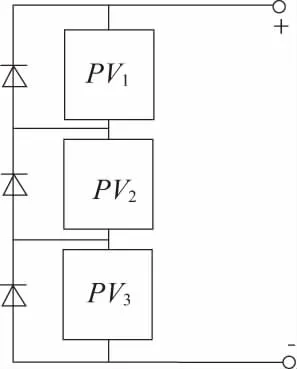
圖2 3塊光伏電池串聯(lián)

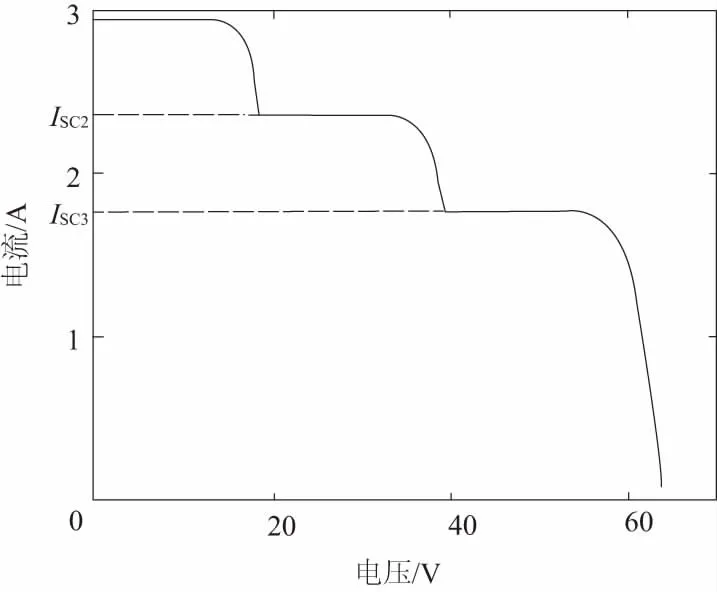
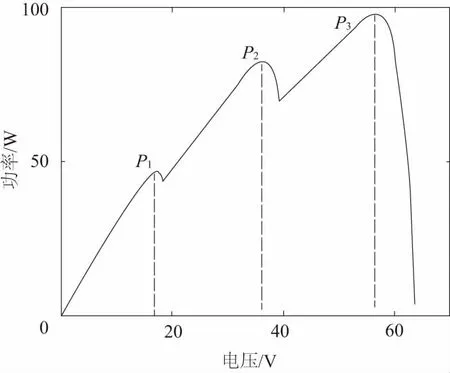
圖3 局部陰影下I-V, P-V曲線

通過上述分析，可推廣到一般情況，當(dāng)串聯(lián)陣列中由n塊電池組件受到局部陰影影響，光照條件不一致時，其I-V曲線會出現(xiàn)n級階梯，P-V曲線將呈現(xiàn)出n個峰值點。文獻[6] 指出，當(dāng)粒子群優(yōu)化算法的粒子數(shù)目和粒子初始位置選取不當(dāng)時，容易造成PSO算法陷入局部最優(yōu)，導(dǎo)致無法跟蹤到最大功率點。

2 改進PSO算法在最大功率跟蹤中的實現(xiàn)

2.1 改進PSO算法

PSO算法作為一種全局搜索算法是多極值函數(shù)尋優(yōu)的有效方法，其原理是初始化一群隨機粒子(隨機解)，然后通過迭代找到最優(yōu)解。每個粒子都具有由速度、位置和目標函數(shù)決定的適應(yīng)度。在每一次迭代中，粒子通過跟蹤兩個極值來更新自己的位置和速度，一個為粒子自身到目前為止的最優(yōu)解，簡稱為個體極值(Pbest)；另一個是整個種群目前找到的最優(yōu)解，即全局極值(Gbest)。種群中任意一個粒子的位置和速度更新方程如下式所示。

(4)

(5)

式中：i表示第i個粒子；k表示迭代次數(shù)；w為慣性系數(shù)；c1和c2為學(xué)習(xí)因子；r1、r2為[0,1] 上的隨機數(shù)；x、v為粒子的位置和速度。

在PSO優(yōu)化算法進行最大功率點跟蹤過程中，慣性權(quán)重w和學(xué)習(xí)因子c1、c2的取值對算法的性能具有重要影響[10]；w取值過大會難于得到精確解，反之，過小會導(dǎo)致陷入局部最優(yōu)；同時，初期設(shè)置較大的c1和較小的c2可避免“早熟”，后期較小的c1和較大的c2可以加速收斂。因此，本文采用了一種自適應(yīng)調(diào)節(jié)的方法，隨著迭代次數(shù)k的增加更新學(xué)習(xí)因子c1和c2并按指數(shù)函數(shù)遞減的慣性權(quán)重，其公式為：

(6)

(7)

w=wstarte-k/kmax

(8)

式中：kmax為最大迭代次數(shù)；c1start,c2start和c1end,c2end為起始和終止學(xué)習(xí)因子；wstrat為初始慣性權(quán)重。

2.2 改進PSO在MPPT中的應(yīng)用

在光伏陣列最大功率點跟蹤中，粒子群算法的適應(yīng)度函數(shù)為測量陣列的輸出功率。將光伏陣列的電壓作為搜索變量，則粒子的位置代表光伏輸出電壓值，其速度即為電壓增量。通過上文可知，PSO優(yōu)化算法粒子數(shù)目和初始位置選擇不當(dāng)會導(dǎo)致跟蹤失敗。因此，粒子個數(shù)應(yīng)大于等于極值點個數(shù)；同時，粒子應(yīng)均勻分布在整個電壓區(qū)間內(nèi)，否則會陷入局部最優(yōu)而導(dǎo)致跟蹤失敗。

由于在最大功率點附近反復(fù)多次迭代會產(chǎn)生長時間的波動，為了避免在最大功率點附近振蕩并使系統(tǒng)快速穩(wěn)定在最大功率點上，本文對PSO優(yōu)化算法設(shè)計了終止策略。當(dāng)各粒子間的最大電壓差<0.5%Uarrray時，即認為找到最大功率點，停止迭代；并將此時所有粒子中對應(yīng)功率最大粒子的值定義為Um，最大功率定義為Pm。

上述方法針對的僅僅是陰影情況固定的MPPT，而在實際情況下陰影和光照強度都會發(fā)生改變，最大功率也隨之變化，所以應(yīng)在算法中加入重啟條件。定義功率變化量p為

(9)

式中Preal為在Um下光伏陣列的實際輸出功率。當(dāng)p大于設(shè)定閾值時，重啟算法，重新尋找最大功率點，其流程圖如圖4所示。

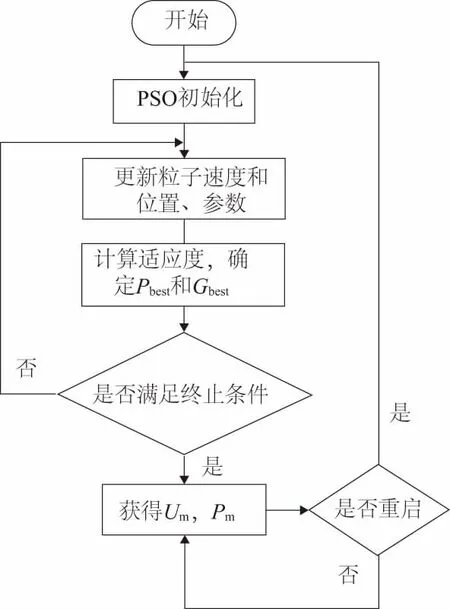
圖4 改進PSO流程圖

3 仿真分析

3.1 仿真模型

為驗證改進PSO優(yōu)化算法在MPPT控制中的正確性，本文在simulink中搭建了基于Boost電路的光伏最大功率跟蹤系統(tǒng)[13]，其系統(tǒng)框圖如圖5所示，其中光伏陣列由3塊MG-P50型光伏電池板串聯(lián)組成。Boost電路的仿真參數(shù)如下：光伏輸入濾波電容C1=200F，直流母線電容C2=1000F，Boost升壓電感L=5mH，負載R=80，開關(guān)頻率為10kHz。

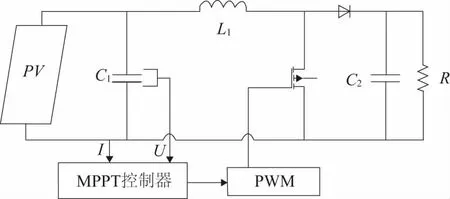
圖5 最大功率跟蹤系統(tǒng)

MPPT控制器模塊中，控制過程為將改進PSO算法中粒子當(dāng)前電壓作為給定電壓，光伏實際電壓作為反饋，通過PID調(diào)節(jié)調(diào)制占空比D，最終實現(xiàn)MPPT。

3.2 仿真分析

仿真時采用3塊光伏電池串聯(lián)組成光伏陣列，并設(shè)計了兩種陰影條件。陰影1條件下3塊光伏電池的光照強度分別為：PV1=1000W/m2,PV2=800W/m2,PV3=600W/m2；陰影2時PV3的光照強度突變?yōu)?00W/m2；兩種陰影下的P-V曲線如圖6所示。陰影1的最大功率和其對應(yīng)的電壓分別為Pm= 98.31W,Um=55.92V；陰影2的最大功率和其對應(yīng)的電壓分別為Pm= 82.56W,Um=36.34V。

圖6 兩種陰影下的P-V曲線

本文在仿真時，選取5個粒子，其初始位置均勻分布在電壓區(qū)間內(nèi)；初始慣性權(quán)重w=0.8；最大迭代次數(shù)為100。首先，在MATLAB中分別編寫兩種算法來驗證算法的正確性，得到的適應(yīng)度(即功率)曲線如圖7所示。從圖中可以看出，改進PSO算法在15代找到了最大功率； 而PSO算法陷入了局部最優(yōu)，并經(jīng)40次迭代才結(jié)束。

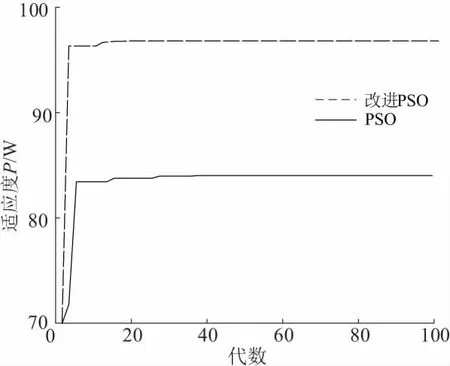
圖7 適應(yīng)度曲線

將MATLAB中的算法改寫成S函數(shù)與Boost電路一同仿真，得到的功率和電壓波形如圖8和圖9所示。PSO算法則經(jīng)過1 s的搜尋找到了最大功率點，其在搜索過程中一度陷入了局部最優(yōu)，最后成功跟蹤到最大功率點；Pm=96W，其功率波動范圍為95.6～96.4W，電壓波動范圍54.3～54.8V。

改進PSO在0.3s時追蹤到了最大功率點Pm=97W，電壓穩(wěn)定值為56V，其電壓和功率跟蹤誤差<1%；其功率波動范圍在97.65～97.85W之間，電壓波動范圍在56～56.3V之間。

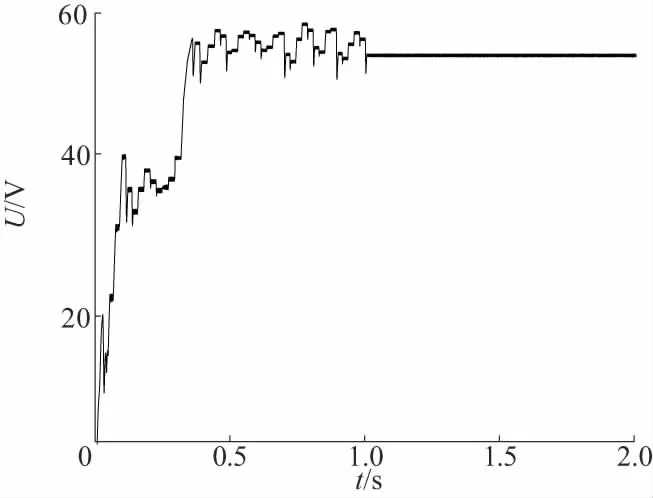
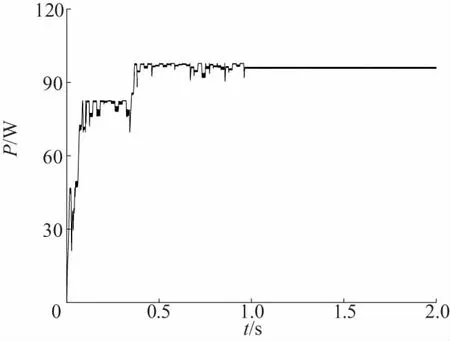
圖8 陰影1下PSO的電壓、功率跟蹤結(jié)果

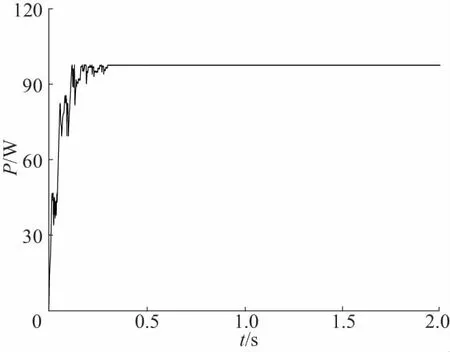
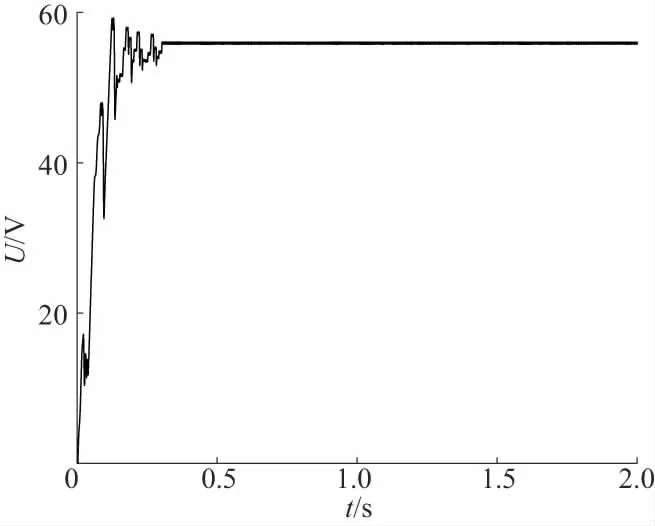
圖9 陰影1下改進PSO的功率電壓、跟蹤結(jié)果

上述只是考慮了靜態(tài)條件，在實際中陰影會發(fā)生突變，因此需要考慮在光照強度發(fā)生突變時算法的有效性。在1s時由陰影1突變?yōu)殛幱?，采用改進PSO算法的MPPT仿真結(jié)果如圖10所示。在由陰影1突變?yōu)殛幱?的瞬間，電壓并未改變但功率快速下降，此時重啟了算法進行尋優(yōu)，經(jīng)過0.3s重新追蹤到了新的最大功率點Pm=82.6W。

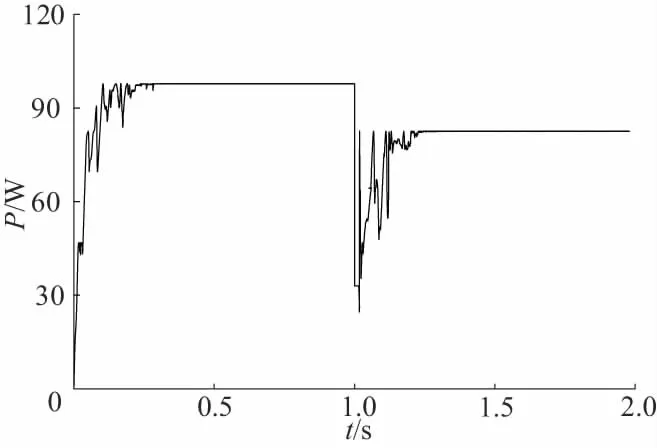
圖10 陰影突變時仿真結(jié)果

4 結(jié)語

本文研究了一種改進的粒子群算法，并將其運用到局部陰影下光伏陣列的MPPT控制中。改進后的粒子群算法的慣性權(quán)重和學(xué)習(xí)因子能夠自適應(yīng)調(diào)節(jié)，克服粒子群算法易陷入局部最優(yōu)的缺點，同時加快了收斂速度。通過仿真表明，經(jīng)過改進的粒子群算法，在靜態(tài)和動態(tài)環(huán)境下都能夠?qū)崿F(xiàn)MPPT，提高了光伏系統(tǒng)的發(fā)電效率。