離散數學模型關聯度檢測方法研究
姚永輝 陸雨


摘要:在大型工程計算分析當中,最難解決的是構建的計算數學模型與實際系統狀態的關聯問題,以及如何對離散數學模型進行修改。基于以上問題,設計離散數學模型關聯度檢測算法,構建出一個檢測離散數學模型關聯度的方法。通過對比實驗證明,設計的檢測方法能夠更加精準的檢測出離散數學模型的關聯度,且通過檢測方法對模型進行改進能夠得出與實際系統關聯度更高的最優模型。
關鍵詞:離散;數學模型;關聯度;檢測
中圖分類號:0158 文獻標識碼:A
文章編號:1009-3044(2020)06-0261-03
將一個實際的問題轉化為數學模型得到相應的理論方程時,其主要的目的是為了讓理論數學模型可以對實際問題進行具體的分析以及運算。離散數學模型的構建是在某一特定的前提條件下提出的,且在構建過程中不考慮其非線性問題的存在,僅僅利用線性完成對模型的構建。伴隨著現代化科學技術的發展,人們對于客觀事實的計算能力已經得到了質的飛躍,因此具備了構建離散數學模型的能力,并且能夠通過數學模型做到對實際系統的模擬,以此可以在最大限度上,滿足實際工程中的應用需求。
1檢測算法設計
1.1相空間重構算法設計
在力學當中,相空間是一種抽象的數學空間。在動力系統當中,相空間是由一組一階方程構成,系統中每一個分量的改變都會與其他分量產生相互的作用。在對離散數學模型的關聯度進行檢測時,最重要的一步是將檢測數據轉換為狀態矢量,即相空間重構。選擇同一時間間隔對數據進行采樣其時間序列可表示為:
公式(1)中,x(t)表示為在t時刻,數學模型的動態學性能;e表示為數學模型嵌入空間的維數;τ表示為數學模型的延遲時間。通過公式(1)的計算,可建立由相空間RE到對應的Re的映射。通過對相空間重構的結果進行分析,可以看出在數學模型中保留了其中原有的動力學性質以及幾何性質。因此可以說明,相空間的重構是時間序列當中的基礎。相空間重構的方法有很多,本文選用一種延遲坐標的方法對相空間進行重構。其重構的主要因素是利用對數學模型延遲時間r和嵌入維數e兩個因素決定。選取延遲坐標完成對數學模型的重構,嵌入維數e表示為能夠完成在狀態轉移過程中構成的最小吸引子的維數大小。在進行實際檢測的過程當中,周圍環境產生的噪聲會對重構結果造成一定的影響,而時序中的噪聲水平越高越會對重構效果造成更大的影響。假設d表示為生成時序向量X(t)數學模型的一個分維數,在重構環境中存在噪聲的情況下,要保證重構的相空間e滿足e≥2d+l,該公式表示為嵌入維數大于吸引子維數適當的整數。因此通過上文研究,從數學角度上,證明了狀態空間重構的有效性。
1.2動力系統算法設計
2離散數學模型關聯度檢測方法設計
2.1相空間重構參數設定
通過對離散數學模型進行上述計算得出相應的響應數據,再將其與實際的結構數據對比,構建一個新的相空間,從而獲取到兩個序列結構的向量,通過對動力信息的數據進行提取以及對離散數學模型與實際結構進行關聯度分析,從而完成對離散型數學模型關聯度的檢測。數學模型數據序列的主要特征包括:在同一個動力系統當中,數據序列的響應能夠代表一個動力系統在某一特定的狀態,從理論角度分析該狀態屬于一個無窮的序列,但在實際檢測的過程中數據序列的數目是有限的。同時,該數據序列與數學模型的離散程度有著密切的聯系;其次,在數據序列當中,其本身隱藏著一個與該動力系統具有密切聯系的信息,并且在信息當中還含有大量的噪聲影響因素;在數學模型當中的向量與從數據序列中選擇的起始點有關,因此需要添加一步位移運算將其消除。
對于一個數學模型的時間序列a1,a2,a3,…,an+(e-1)通過重構相空間算法,計算出引人恰當的嵌入維數和時間延遲,構成一個完整的矩陣或向量。其表達式為:
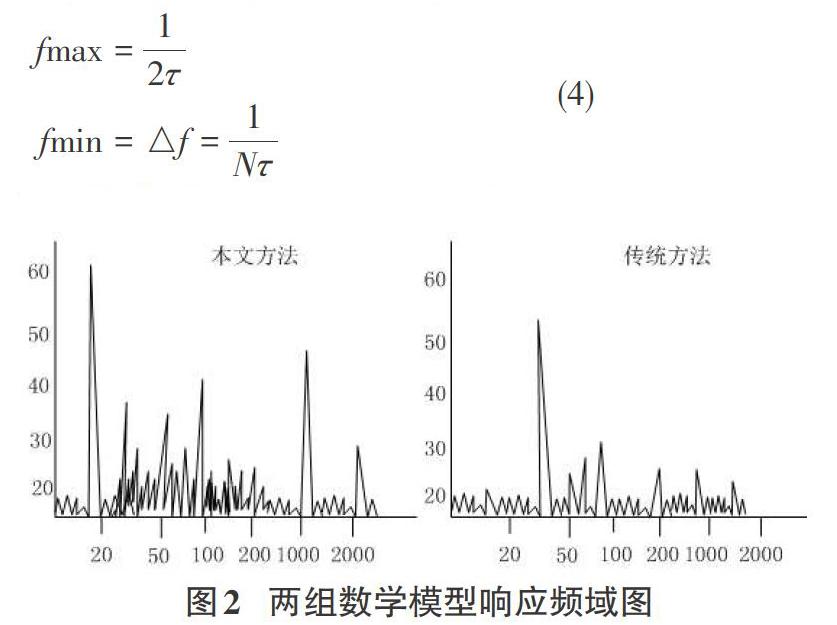
公式(2)中,A表示為構造向量;e表示為嵌入維數;τ表示為時間延遲。通過該表達式對被檢測的數據固定時間進行延遲,從而構成一個多維度狀態的空間。通過不斷的重復提取出在不同時刻下各個延遲量,從而產生對e維相空間相點的變化軌跡。對數學模型的數據序列進行關聯度檢測方法流程設計圖,如圖1所示。
在對數學模型進行瞬態激勵作用下,動態響應的是數學模型整體的動態信息,因此維數要盡可能選用數值較大的,才能保證恢復其實際的動力系統信息,同時也可以有效保證數據模型數據的噪聲干擾以及結構系統動力學信號完整。
2.2有限元結構動力分析方法設計
有限元結構的基本前提是將連續的求解域進行離散處理,從而構成一個有限個數單元的組合體。通過構建的組合體,可以對數據模型的區域進行求解。而另一種方法,是利用每一個單元中的假設近似函數,將其表示為全部待求解的未知函數。離散數學模型的有限元分析可分為如下幾個步驟:
第一步,對數據模型中的連續區域進行離散處理;
第二步,根據數據模型中的數據樣本構造一個適當的插值函數;
第三步,構建一個具有單元特性的矩陣,一個具有數學模型整體特性的矩陣;
第四步,將整個數學模型的運行方程導出,其方程可表示為:
方程(3)中,[M]表示為質量矩陣;[c]表示為阻尼矩陣;[K]表示為剛度矩陣;[P(t)]表示為整個數學模型的運行模式;
第五步,通過計算,求出數學模型的運行方程。
2.3有限元結構動力分析具體流程
利用有限元結構動力分析方法對數學模型中的有限元動力響應進行求解,求解方法如下所示:
在進行求解前,首先要在程序中構建一個全新的文件,并將其對應的初始參數設置為0,從而為后續的計算保留出足夠的計算空間和存儲空間。
步驟1:在處理分析程序的初始模塊中,計算出數學模型中所有的有限單元,同時預設計算過程中的相關參數,再利用有限元結構動力分析軟件中的建模工具,構建一個與其相符的數學模型,對于造成數學模型影響不大的條件,例如載荷、約束等,進行適當的簡化。以所需分析的問題作為基礎,選取合適的網格劃分方法,對該數學模型進行劃分處理,在完成一系列操作后,退出該模塊;

