論容阻電路中導體棒的運動
葉正勇
(浙江省衢州二中,浙江 衢州 324000)
切割情形下容阻電路的典型模型,其示意圖如圖1.

圖1
圖1中,質量為m、有效切割長度為l、棒有效電阻為r0導體棒通過導軌與定值電值R0及電容器C(開始不帶電)構成閉合回路.導體棒在平行于導軌的恒力F作用下由靜止開始沿導軌運動;整個導軌處于垂直于導軌平面的勻強磁強B中,假定導軌足夠長而電阻不計.試分析導體棒將如何運動?回路中的電流及電容器所帶電荷量如何隨時間變化?上述過程中能量如何轉化?
1 電學量分析
1.1 回路中的電流i如何隨時間變化?
從棒開始運動時刻開始計時.由題意,t=0時,各物理量的值(初始值)分別為:電流i0=0,電容器的電荷量q0=0;棒的初速度v0=0,棒的初始加速度a0=F/m.
圖1中,對任一時刻t,設電容器上極板的電荷量為q,回路的電流為i,導體棒的速度為v,則
(1)
(2)
其中:R=R0+r.
(3)
將(2)式對時間t求導得
將(1)、(3)兩式代入上式化簡有
此式即回路中的電流i滿足的微分方程.結合初始條件i0=0,解得
(4)
令
(5)
(6)
(5)式簡化為
i=IS(1-e-λt).
(7)
(7)式表明:回路中的電流隨時間按指數函數增加,且增加到一定的值后保持不變(見i-t圖像).
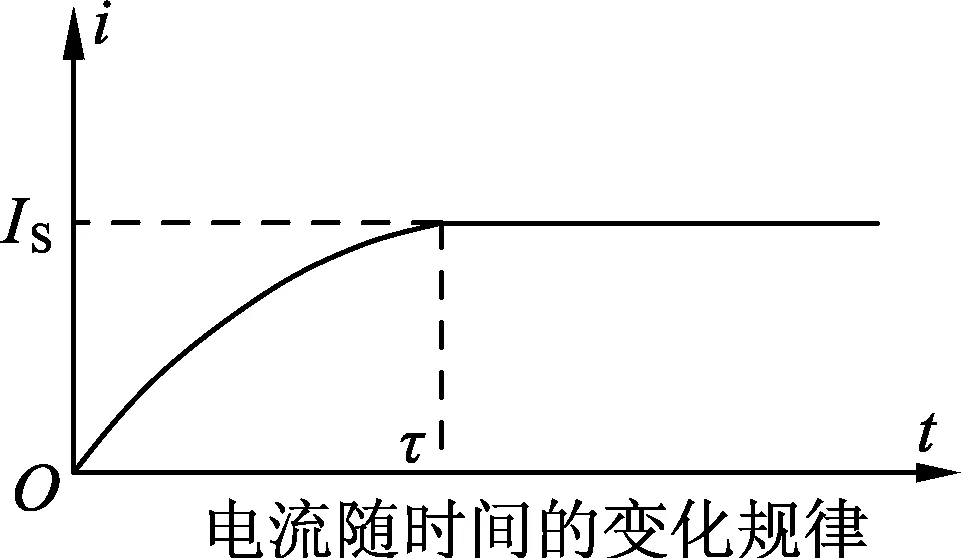
圖2
1.2 電容器的電荷量如何隨時間變化?
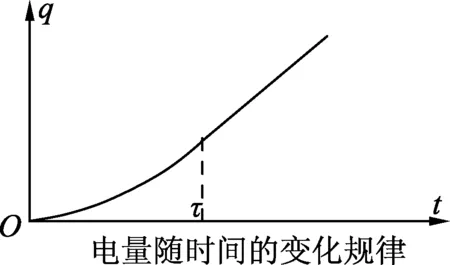
圖3
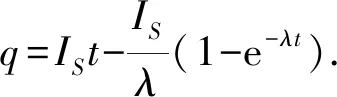
在i-t圖像中,q等于圖像圍成的面積,由此可定性畫出q-t圖像(見圖3),可見電荷量隨時間的變化情況是,電荷量隨時間的增加而增大,且電荷量的時間變化率(電流)隨時間先增加后保持不變.
2 導體棒運動情況分析
2.1 導體棒的加速度如何隨時間變化?
將電流隨時間變化的(7)式和(5)式代入(3)式可求得棒的加速度a,
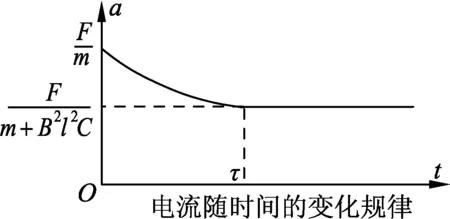
圖4
由此可畫出a-t圖像(見圖4),可見棒的加速度隨時間按指數函數減少,且減到一定的值后保持不變.
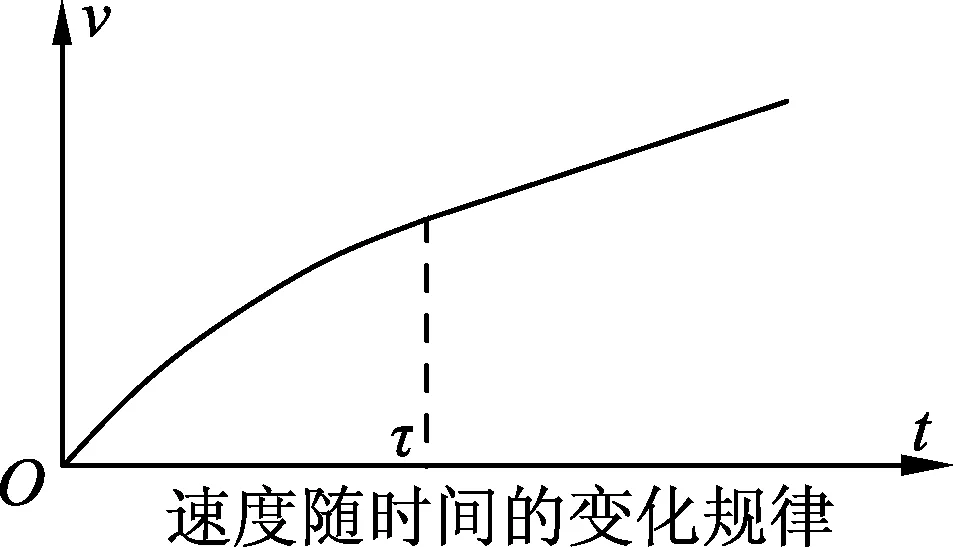
圖5
2.2 導體棒的速度如何隨時間變化?
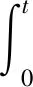
在a-t圖像中,v等于圖像圍成的面積,由此可定性畫出v-t圖像(見圖5),可見棒先做加速度不斷減少的非勻加速運動,后做勻加速運動.
3 系統中的能量轉化與守恒分析
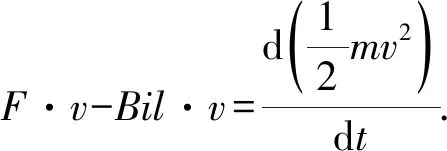
同時,導體棒在電路中又是電源,是提供電能的裝置,根據電路中的能量守恒:電源的總功率等于內、外電路中所有電器消耗的總電功率,故對時刻t又滿足
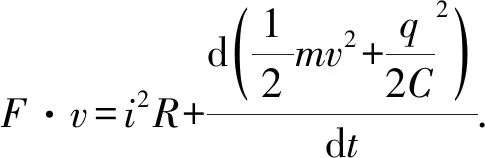
此式給出了整個系統的能量守恒關系,它表明,外界提供給系統的能量(用外力F做的功量度)最終轉化為電路中內、外電阻上增加的內能、電容器內增加的電場能以及導體棒增加的動能;且數值上等于三者之和.
可以證明,將前面求得的i、q、v、a的表達式代入此能量關系式恒成立.
綜上所述,切割情形下的容阻電路模型,具有以下明顯特點:
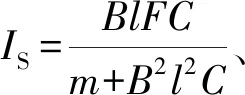

(3) 該模型系統的能量轉化與守恒體現在,系統總能量(電阻器的內能,導體棒的動能以及電容器的電場能的總和)的增加量等于外界輸入到系統的能量(通過外力做功).
(4) 本模型中電流,加速度,速度隨時間的變化情況也適用于純電阻切割模型和純電容切割模型.純電容模型可視為本模型在R→0時的特例;純電阻模型可視為本模型在C→∞時的特例.

