彈簧擺到底能擺多高?
——由一道高三聯考題引發的思考和研究
江俊勤
(廣東第二師范學院物理與信息工程系,廣東 廣州 510303)
1 衡中同卷——2019年全國高三聯考理綜卷第21題及其答案
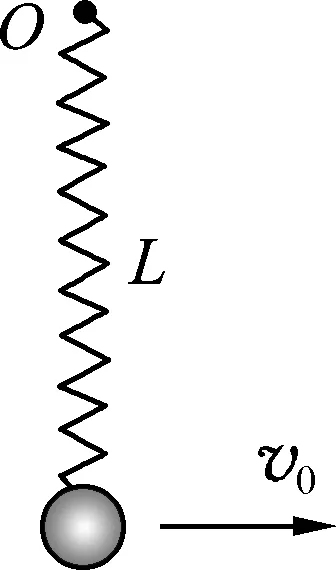
圖1 彈簧與小球的初始狀態

(A) 彈簧的最大長度大于L.
(B) 小球到達的最高點高于O點.
(C) 小球到達的最高點與O點等高.
(D) 小球到達最高點時彈簧彈力為0.
試題答案與解析: (A)、(B).

2 用機械能守恒定律做定性分析
原考題所給的答案“選項(B)正確,(C)錯誤”明顯是一個想當然的武斷結論、其解析也邏輯混亂,錯誤地認為開始時系統的機械能mv02/2+EpF>mgL就保證了小球到達的最高點高于O點. 在原題答案的解析中,明顯漏掉了最高點處小球可能有較大的動能mvx2/2 (x為水平方向,y為豎直方向,O為坐標原點;如圖2所示),也沒有考慮小球在最高點時的彈力勢能,這兩項的大小將直接影響著小球所能到達的高度,下面先從機械能守恒定律出發進行定性分析.
設彈簧的勁度系數為k,松弛狀態(自然狀態)的長度為L0,最高處小球的縱坐標為ymax、彈簧的長度為l;以小球的初始位置為重力勢能的零點,則開始時系統的機械能為mv02/2+EpF=mv02/2+k(L-L0)2/2>mgL;在最高點處系統的機械能為mvx2/2+k(l-L0)2/2+mg(L+ymax).由機械能守恒定律得
mv02/2+k(L-L0)2/2=mvx2/2+k(l-L0)2/2+mgL+mgymax.
(1)
式(1)右邊前兩項mvx2/2和k(l-L0)2/2的大小都是未知的,從題設條件我們并不知道mv02/2+k(L-L0)2/2是比mvx2/2+k(l-L0)2/2+mgL大還是小,故不能確定ymax>0還是ymax≤0,即無法保證小球到達的最高點高于O點!
小球到底能擺多高?小球到達的最高點能不能高于O點?為了徹底解答本問題,必須從牛頓第二定律出發進行定量分析.
3 動力學方程和數值分析
(2)
由牛頓第二定律可知擺球的動力學方程為
(3)
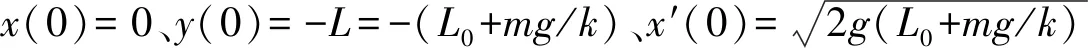
本文固定取m=0.1 kg,L0=0.5 m,而k取各種不同數值進行求解. 先取較小的勁度系數,例如k/m=110 N/(m·kg)(即m=0.1 kg、k=11 N/m),則擺球在1.5 s、12 s和180 s內的運動軌跡分別如圖2~4 所示,球到達的最高點自始至終都低于O點,即選項(B)“小球到達的最高點高于O點”是不能實現的.
小球處于平衡時合力為0,突然獲得一水平速度后沿水平方向做直線運動并開始拉伸彈簧(所以選項(A)正確),隨著彈簧長度增加拉力增大,小球向上做曲線運動(然后彈簧開始處于壓縮狀態);第一次到達最高點(嚴格來說應稱為y的極大值點)處之后受外推彈力作用向右下方運動,第一次到達最低點處(y的極小值處)在慣性和彈簧力拉扯下向左上方向運動,并跨越中線(x=0)到達左邊,如圖2所示,在1.5 s內小球的運動軌跡開始呈現出“上下左右反復”的復雜性;圖3給出了12 s內的運動軌跡,小球的運動軌跡雜亂無章、左右不對稱;但經歷足夠長的時間后,運動軌跡表現出規律性——小球運動軌跡被限制在某種帶狀的有限區域內并呈現出大體上的左右對稱,180 s內的運動軌跡如圖4所示.
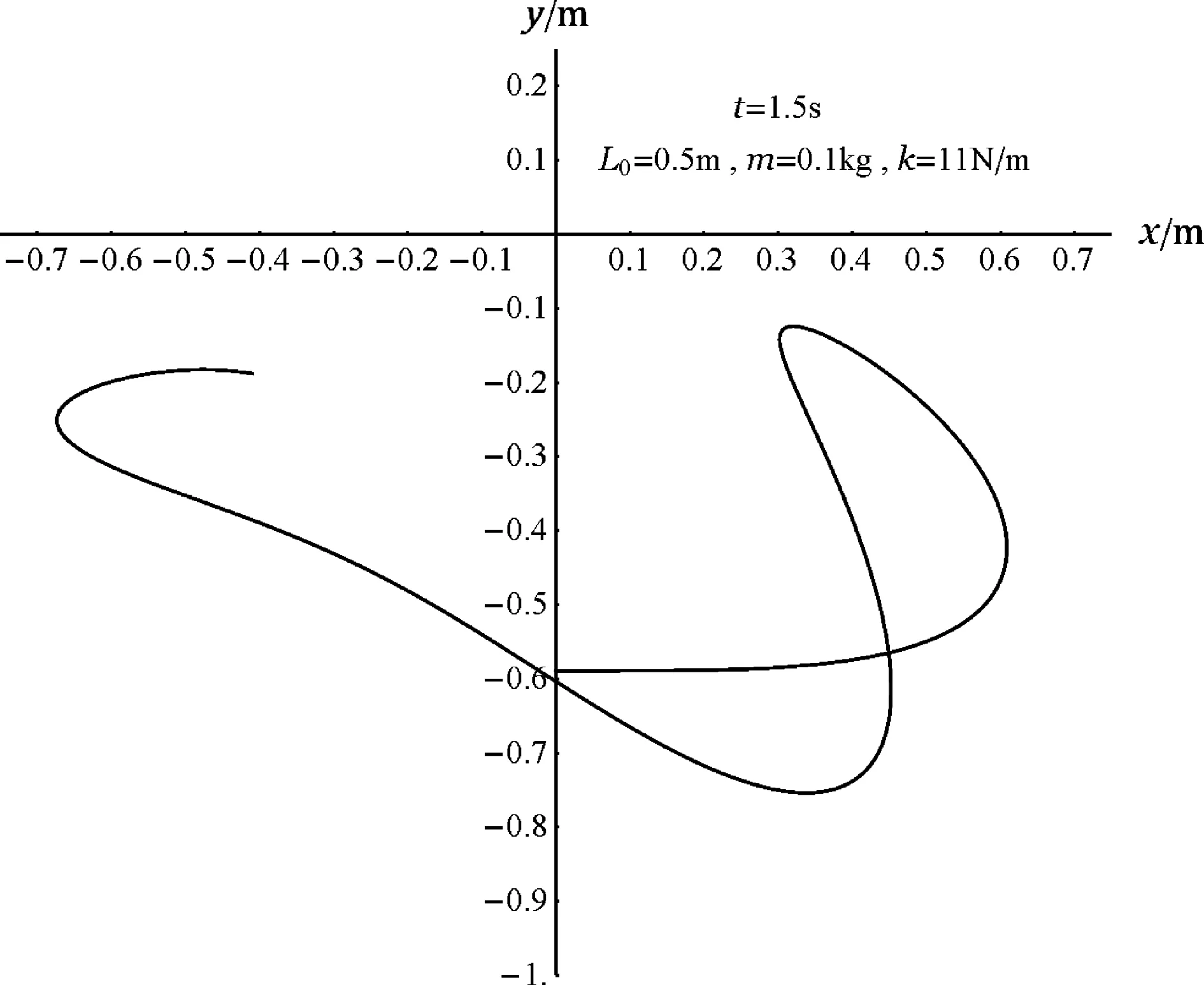
圖2 當k/m=110 N/(m·kg)和L0=0.5 m時,小球在1.5 s內的運動軌跡
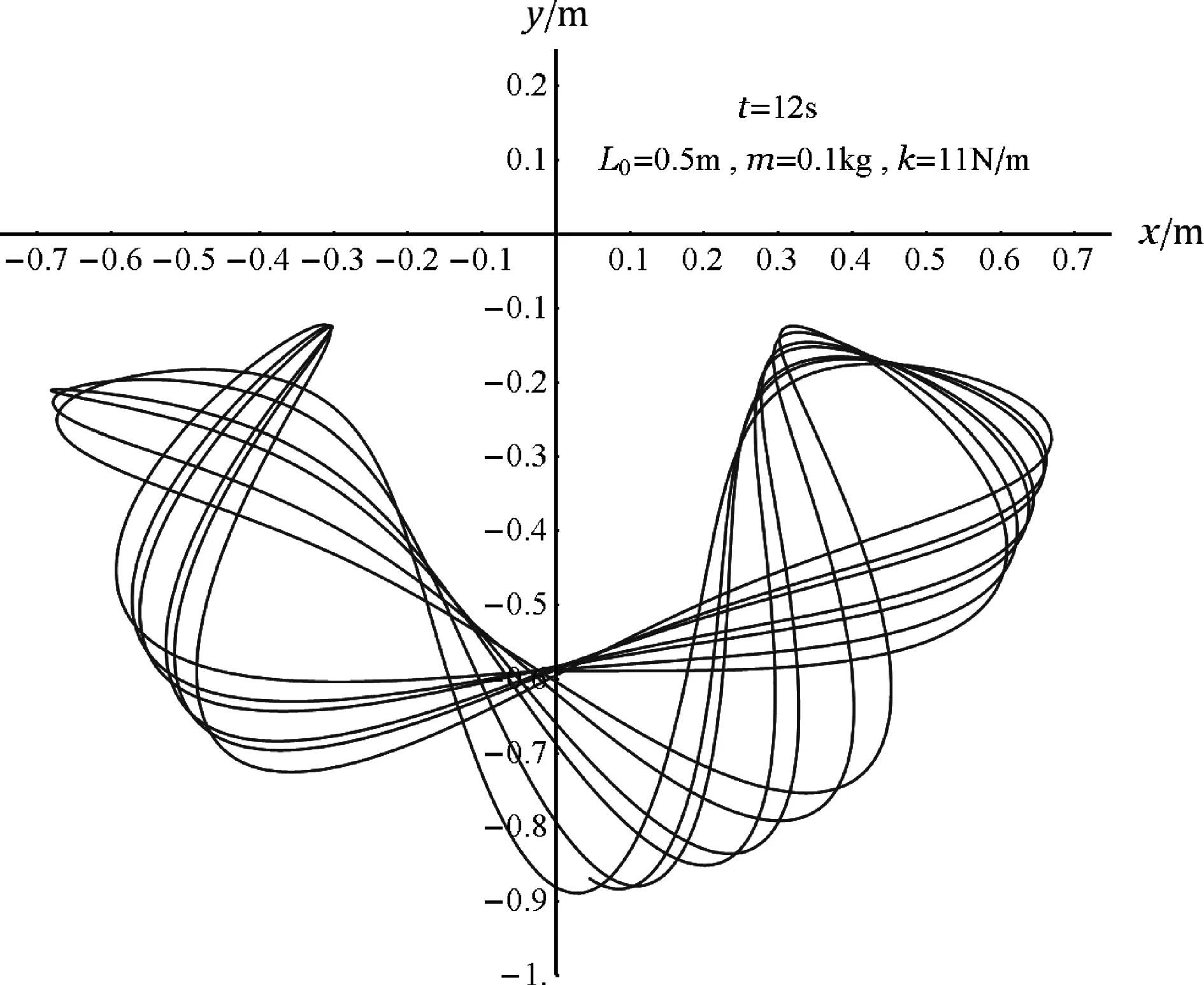
圖3 當k/m=110 N/(m·kg)和L0=0.5 m時,小球在12 s內的運動軌跡

圖4 當k/m=110 N/(m·kg)和L0=0.5 m時,小球在180 s內的運動軌跡
圖2~4顯示:當k/m=110 N/(m·kg) 時, 最高點處小球具有較大的動能mvx2/2或較大的彈力勢能k(l-L0)2/2,所以雖然mv02/2+EpF>mgL,但小球的最高點低于O點(ymax<0). 更多的模擬表明在k/m≤134 N/(m·kg) 時都是如此.
若取大一些的勁度系數, 如k/m=150 N/(m·kg)(即m=0.1 kg、k=15 N/m), 則擺球在1.5 s、3.5 s、12 s和180 s內的運動軌跡分別如圖5~8 所示.
從圖5~圖8可知,當k/m=150 N/(m·kg) (即m=0.1 kg和k=15 N/m)時,能實現擺球到達的最高點高于O點. 但是,在小球向上運動的過程中,不是每次擺到“最高點(嚴格來說是高處反轉點或y的極大值)”都高于O點,更不是一開始就能高于O點:圖6顯示直到第3.5 s前夕的第四個高處反轉點時才第一次出現高于O點的機會,圖7表明前12 s內才有兩次出現高于O點的情況(當ymax>0時該極大值點處小球的動能和彈力勢能都較小).

圖5 當k/m=150 N/(m·kg) 和L0=0.5 m時,小球在1.5 s內的運動軌跡
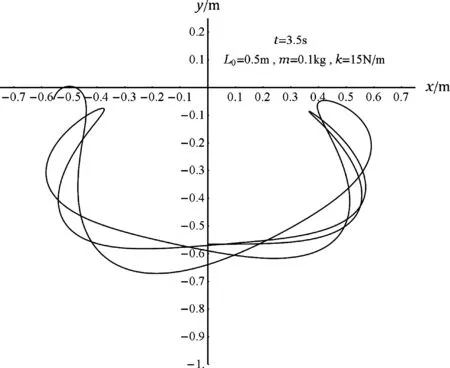
圖6 當k/m=150 N/(m·kg)和L0=0.5 m時,小球在3.5 s內的運動軌跡
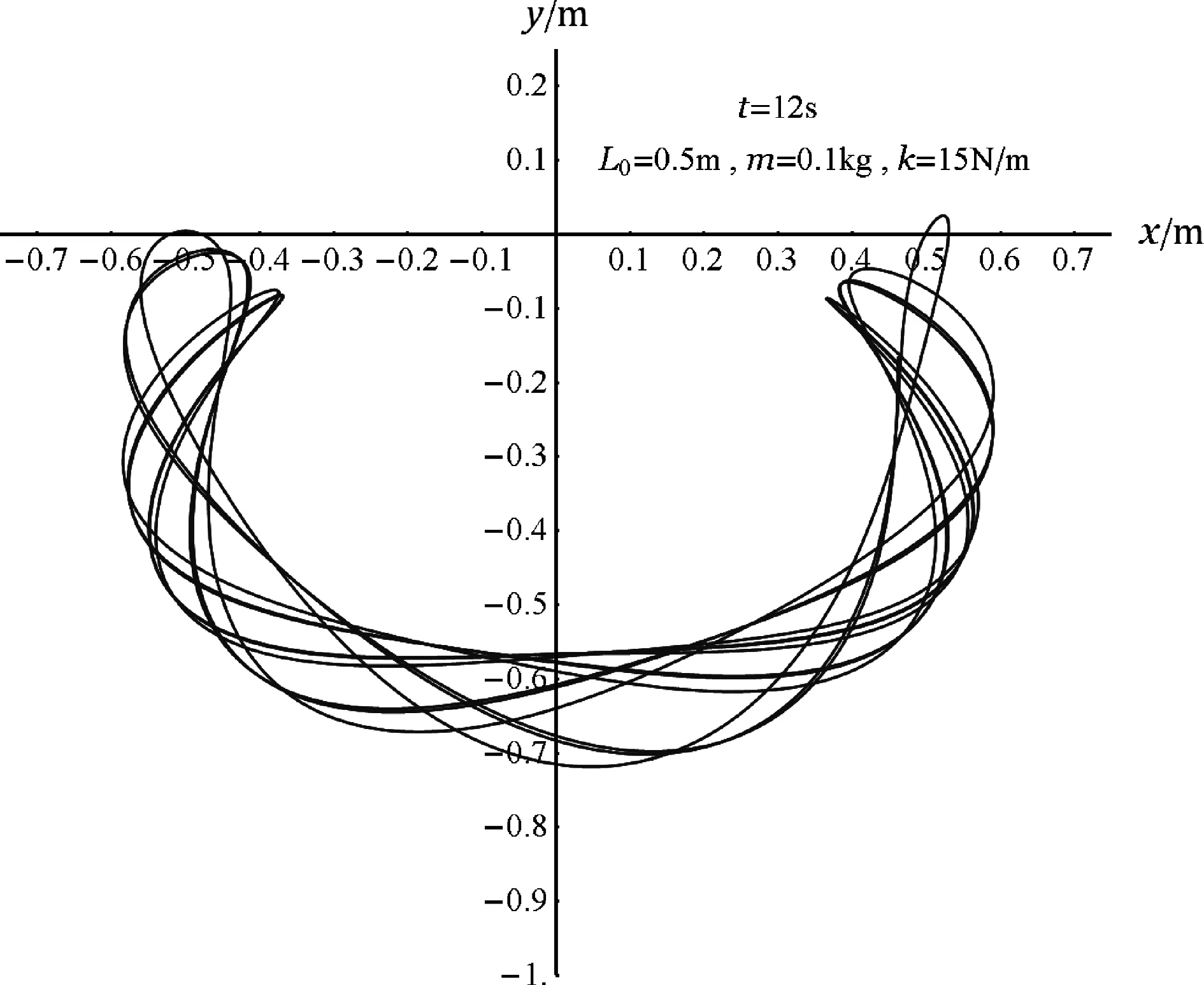
圖7 當k/m=150 N/(m·kg)和L0=0.5 m時,小球在12 s內的運動軌跡

圖8 當k/m=150 N/(m·kg)和L0=0.5 m時,小球在180 s內的運動軌跡
進一步的數值結果表明:只要134 N/(m·kg) 取更大的勁度系數,例如k/m=200 N/(m·kg) (即m=0.1 kg 、k=20 N/m),則擺球在180秒內的運動軌跡如圖9所示,小球到達的最高點又是都低于O點. 圖9 當k/m=200 N/(m·kg) 和L0=0.5 m時,小球在180 s內的運動軌跡 本文先從機械能守恒定律出發對2019年全國高三聯考理綜卷第21題進行了定性討論,結果表明:從機械能守恒定律出發無法判斷擺球到達的最高點能不能高于O點,考題的原答案及其解析都是欠妥的. 為了讓問題有明確的答案,本文接著從擺球遵循的牛頓第二定律出發、使用著名通用軟件Mathematica對該問題進行具體深入的數值計算和檢驗,由具體的計算結果可以得出如下結論: (1) 選項(A)“彈簧的最大長度大于L”是正確的. (2) 選項(B)“小球到達的最高點高于O點”不一定能實現,只有小球質量m和彈簧勁度系數k滿足某些特殊條件才能實現,若取m=0.1 kg和L0=0.5 m,則只有勁度系數在較狹窄的范圍內13.4 N/m (3) 既然在m和k滿足某些特殊條件可以實現小球到達的最高點高于O點,那么選項(C)“小球到達的最高點與O點等高”的可能性就不能完全排除在外. 總之,小球到達的最高點能否高于O點由彈簧的自然長度L0和勁度系數與小球質量的比值k/m共同決定,本考題的原答案及其分析都是不對的,它給物理教師的警示是:在設計新型題目時務必小心謹慎,最大限度地避免“想當然”. 公開推出新題之前應該從大學物理的高度認真審視其科學性,如果遇到沒有簡單解析解而無法得出明確結論的情況,則最好能利用通用軟件進行數值檢驗.
4 結論與討論

