浙江省2019年4月物理選考卷第23題分析及教學拓展
嚴建麗
(浙江省湖州中學,浙江 湖州 313000)
1 原試題的呈現和分析
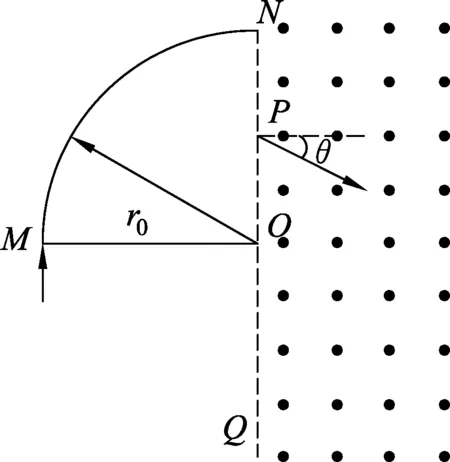
圖1
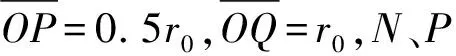
(1) 求靜電分析器中圓弧軌跡處的電場強度E0和磁分析器中的磁感應強度B;
(2) 求質量為0.5m的離子打在探測板上的位置與O點間的距離l;
解析:題中帶電粒子在直線邊界勻強磁場中的運動在中學里是為大家之熟悉,而徑向電場則突破了以往定量計算帶電粒子運動的勻強電場.此題將徑向電場和直線邊界勻強磁場完美地結合,充分體現了考題設計的智慧.試題的場景和設問,考生是熟悉的,入口也很柔.第(1)問求離子運動軌跡處的徑向電場強度以及磁分析器中的磁感應強度,由徑向電場力和洛侖茲力分別提供離子做圓周運動的向心力,就能得到結果,簡單直接.第(2)問鑒于考綱的限制,并沒有糾纏于離子在電場中運動的路徑,試題通過直接給出質量為0.5m離子從徑向電場出射時的位置和方向,只討論在磁場中運動的情況,成為離子以一定角度入射直線邊界磁場中的典型問題.第(3)小題作為試卷最后的壓軸之問,集中了質譜儀模型中不同質量離子以不同速度、不同方向、在不同位置入射時,因磁場發生波動而致使離子束打在探測板上位置發生重疊的問題,內容多、設問新、難度大,是很好的壓軸之問.
2 挖掘試題隱含的物理內涵
帶電粒子在徑向電場中運動有著豐富的物理內涵,但試題因考綱限制而將其隱去,使此題成為高考可考之題,可見命題者的良苦用心.然而,從教學角度來講,此題有許多可以進一步挖掘的教學價值.下面分析此題背后的物理內涵,并進行一些拓展討論.
2.1 質量為0.5m離子在靜電分析器中出射速度的解法賞析
徑向電場在工程技術中有許多應用,可由帶等量異號電荷的兩同心球面、兩同軸柱面或孤立的點電荷等帶電系統產生.試題中的徑向電場,沒有具體說明是如何產生的,但孤立的點電荷產生的徑向電場與本題給出的條件是自洽的,即若電場強度
(1)
其中Q為點電荷電量,k為靜電常量,由于質量為m的離子軌跡處的電場強度
(2)
則電量Q與靜電常量k滿足
(3)
上式出現負號是考慮到離子帶正電.由方程(3)就可得到題設中的N、P兩點間的電勢差
(4)
因此,本題的徑向電場可認為是帶電荷量為Q的點電荷產生的.
認識到本題徑向電場的形成,我們就可以挖掘試題背后的物理規律.分析考題為什么要給出題設中的一些條件,而且求解質量為0.5m的離子從靜電分析器中出射的速度時,可以有更多的方法.
解法1:離子沿圓周運動時,其徑跡為等勢面,靜電場是保守場,做功與路徑無關,由動能定理,有(高考試題給出的標準解答)
(5)
解法2:離子在保守場中運動,由能量守恒定律,有
(6)
解法3:此題的徑向電場為平方反比力場,類比引力場,開普勒第二定律在本題的徑向電場中仍然適用,于是有
(7)
解法4:徑向電場為有心力場,角動量守恒(本質與開普勒定律一致),有
0.5mv0r0=0.5mvrsin(90°+θ).
(8)
2.2 質量為0.5m離子在靜電分析器中的軌跡、出射位置和方向的進一步討論
為了避免高考試題超綱,本題直接給出了質量為0.5m離子的出射位置和方向.在教學中我們可在上述分析的基礎上,與我們熟悉的引力場作一類比,稍稍拓展一下所學知識,就能讓學生知其所以然.題中“別有洞天”的情境會大大開闊學生的物理思維和物理眼界,有學習的獲得感.
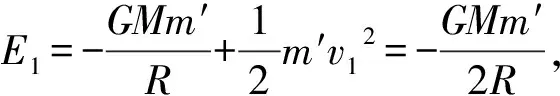
衛星做橢圓運動,其半長軸與機械能有如下關系
(9)
所以,只要已知系統的總能量,衛星的運動軌跡就完全確定了.點電荷系統與行星系統類似,也有相同的規律.因此,對于質量為0.5m、以同樣速度v0運動的離子,其總能量
(10)

圖2

(11)
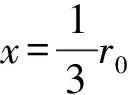
方程(11)兩邊對x求導數,得

3 徑向電場中離子運動的一般性討論及教學拓展
本題還可以進行一般性討論,若設離子質量m″=m(1+γ),考慮離子做橢圓運動,要求離子的能量E<0,即
(12)
由于質量為正,故γ的取值范圍為-1<γ<1.
通過與上述類似求解,可得粒子的運動方程為
(13)
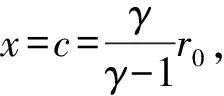
方程(13)兩邊對x求導,可得到離子出射方向與水平方向的夾角的余弦,即
(14)
顯然,高考試題是γ=-0.5時的特例.
掌握了離子在徑向電場中運動的一般規律,在教學上就可以進行一些有益的拓展.比如在原試題的基礎上,我們可以討論質量為1.5m的正離子在靜電分析器中的運動軌跡、出射位置、出射速度等問題.

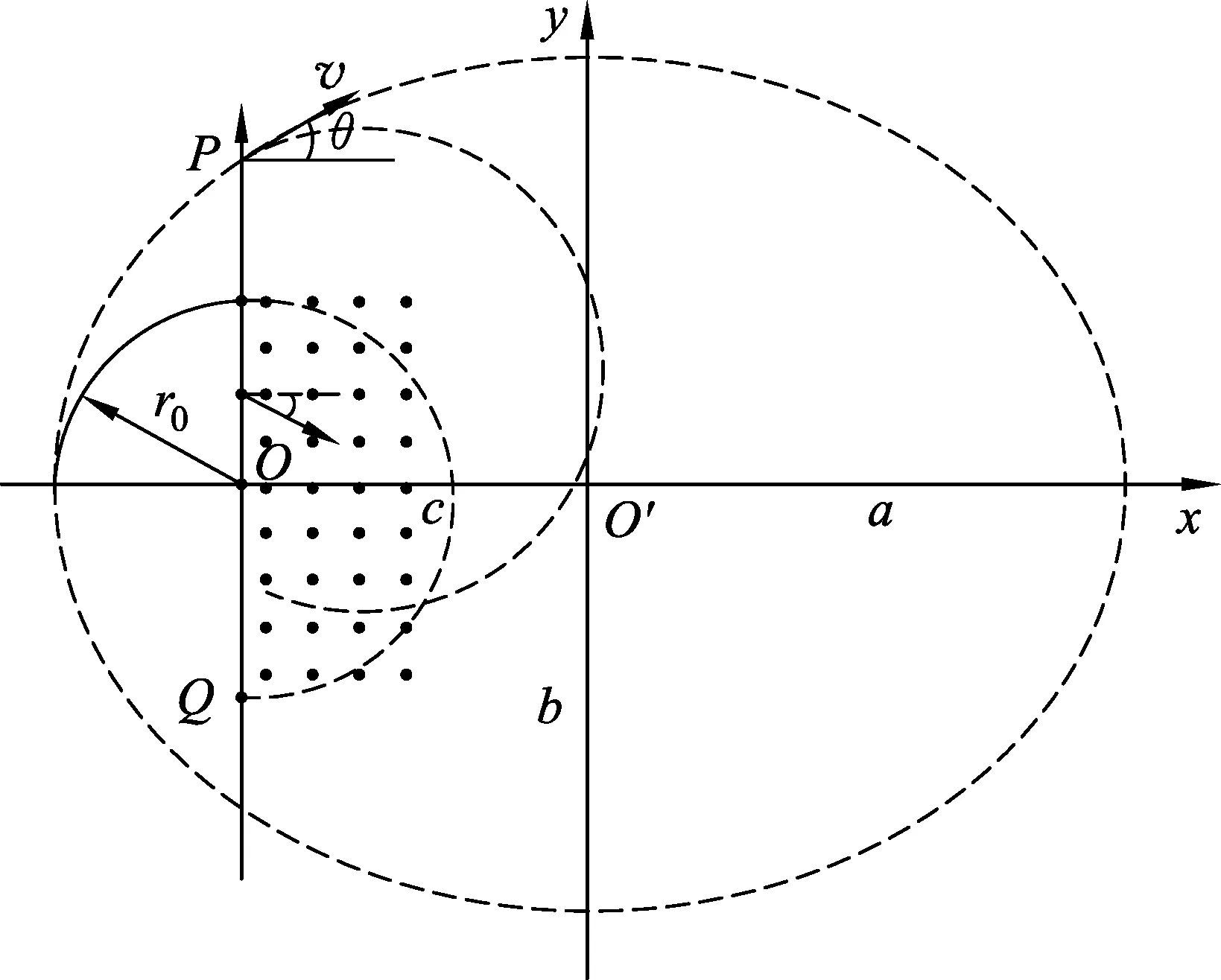
圖3
離子出電場后,經磁場偏轉,然后打在探測板的位置與O點的距離為
1=2rcosθ-1.5r0=0.5r0.
因此,如果質量分別為m和1.5m的兩離子束進入這雙聚焦分析器,可將高考題中的第(3)小題遷移到這里來進行同樣的設問.上述分析表明,質量為0.5m與1.5m的離子從靜電分析器中的出射位置、出射方向是對稱性的,因此,在磁分析器中兩束離子不發生重疊時允許磁場波動的條件與高考題是一樣的.

圖4
這樣類似的拓展可以根據教學的需要設置.挖掘高考試題隱含的物理思想,總結其規律,能打開學生的學習思路.特別是面向一些要參加自主招生或競賽的優秀學生,深入進行這樣的物理內涵的挖掘,學習思路上的類比、遷移和拓展,是非常有必要和有意義的.

