從相位傳播的角度計算多普勒頻移的“降階”方法
——對一道全國中學生物理競賽復賽試題解答的思考
鄭金山
(莆田第四中學,福建 莆田 351100)
第32屆全國中學生物理競賽復賽試題第4題,設置了機載測地雷達的電磁波多普勒頻移的討論. 其中第1問的原參考解法,從電磁波中的相位傳播的角度進行計算. 由于采用了解析幾何的框架,演算比較復雜. 根據其思路,在給高中生講解時,借鑒《力學》[1]教材中的處理,嘗試通過結合信號傳播路徑的幾何關系,計算信號傳播時間,分析多普勒頻移,降低了計算的難度.
1 原題及解答思路

圖1
(32屆全國中學生物理競賽復賽第4題1問)[2]如圖1,飛機在距水平地面(xz平面)等高的航線KA(沿x正方向)上,以大小為v(v遠小于真空中的光速c)的速度勻速飛行;機載雷達天線持續向航線正右側地面上的被測固定目標P點(其x坐標為xP)發射扇形無線電波束(扇形的角平分線與航線垂直),波束平面與水平地面交于線段BC(BC隨著飛機移動,且在測量時應覆蓋被測目標P點),取K點在地面的正投影O為坐標原點. 已知BC與航線KA的距離為R0. 天線發出的無線電波束是周期性的等幅高頻脈沖余弦波,其頻率為f0. 已知機載雷達天線經過A點(其x坐標為xA)及此后朝P點相繼發出無線電波信號,由P反射后又被機載雷達天線接收到,求接收到的回波信號的頻率與發出信號的頻率之差(頻移).

原解答過程[2]對數學運算能力的要求比較高,為了便于直觀理解,筆者嘗試從兩個信號(余弦電磁波脈沖)的傳播路徑的幾何關系入手,分析兩個時間間隔的關系. 由于采用幾何的方法,比較直觀,高中生更為熟悉,可以降低學習難度.
2 從幾何直觀上分析,考慮信號傳播過程進行求解

圖2
如圖2所示,先把三維的空間描述,轉換為二維平面上的情形.當飛機飛到A點,從波源發出一個波峰(僅為了便于理解,當然可以是某個其它的相位)開始計時,這個波峰相位向空間傳播,遇到目標P發射回來,接收器接收到了這個波峰的回波信號. 在波的傳播過程中,實際上飛機載著雷達以飛行速度沿航線運動. 這時飛機已經飛到了A′點.在發出第1個波峰之后,過了1個周期(源周期)τ的時間,當飛機飛到B點時,下一個波峰信號(或者延后了2π的相位)從雷達出發,向空間傳播,同樣被目標P反射后,接收器接收到了它的回波信號. 此時飛機飛到了B′點. 接收器接收到的兩個信號的時間間隔,即為接收到的信號的周期τ′. 如果能夠得到發射周期(源周期)和接收周期的關系,就可以計算出接收到的頻率.
假定在t1時刻,第1個波峰從A出發,到達P反射回來,到點A′被接收. 設所用的時間為t,有

(1)
信號到達A′的時刻為
(2)
當飛機飛到B處時,發出下一個波峰信號,此時刻為t2=t1+τ,此信號傳播出去,遇到P反射回來,到B′點被接收. 設所用的時間為t′,有

(3)
信號到達B′的時刻為
(4)
相鄰兩個波峰到達接收機的時間間隔

(5)
需要借助輔助線討論,從B′作B′D⊥A′P于D,從B作BE⊥AP于E.


(6)


(7)

(8)
在直角三角形ΔA′DB′中,

(9)
式(9)中θ=∠B′A′D.
在直角三角形ΔAEB中,

(10)
式(10)中φ=∠BAE.
由幾何關系∠B′A′D=∠BAE+∠A′PA,令δ=∠A′PA,則有θ=φ+δ. 討論式(9)和式(10)中兩個角的余弦,有
cosθ=cos(φ+δ)=cosφcosδ-sinφsinδ,
(11)
由(6)可知,δ是一個小角度,δ?1,cosδ≈1,sinδ≈δ,由式(11)得
cosθ=cosφ-δsinφ.
(12)
代入式(9),有
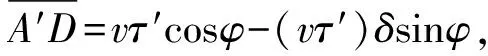
(13)
由式(6),vτ′是長度的一階小量,δ是弧度一階小量,sinφ是一個隨飛機飛行位置變化的有限數值,所以(vτ′)δsinφ是一個長度的二階小量,可以忽略. 式(13)可以變形為

(14)
將式(7)、(8)、(10)、(14)代入(5)可得

(15)
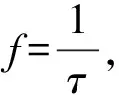
(16)
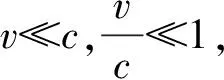

(17)
(18)
這里,飛機飛行的航線和從飛機射向目標P的光線的夾角為φ,飛機還未飛到F,此時飛機和目標之間是靠近的趨勢,cosφ>0,Δf=f′-f0>0,f′>f0,表現為頻率變大的現象;若飛機飛到F點,cosφ=0,沒有頻率差;若飛機飛過了F,cosφ<0,飛機和目標之間是遠離的趨勢,表現為接收到的頻率比源頻率減小的現象. 這和教材[3]中的討論是一致的. 從圖2中可以看出,產生信號周期差的原因是由于信號回程時少走了一段路程,導致接收到的信號周期比源周期小.
3 進一步的思考
以上通過分析兩個相隔一個周期(相位相差2π)的波峰信號的傳播過程,求解出多普勒效應中的接收到的信號周期和源信號周期的關系,從而求出頻率差.這種方法同樣適用于教材[3]中的幾種情況的討論: (1) 波源相對觀察者運動,觀察者靜止; (2) 波源靜止,觀察者相對波源運動; (3) 超聲波雷達測速,雷達不動,目標相對雷達運動. 這些情境中的頻移討論,也可以從相位傳播的角度,應用幾何路徑分析的方法進行計算.
4 對解答的反思
原題解在坐標系中嚴謹的進行了代數解析,運算要求較高,可以作為更高的要求去學習掌握,具有更廣闊的應用前景,例如這樣可以更方便的編制程序進行數值計算等. 本文的討論可以作為一個過渡,為學生理解原解答打下基礎. 另外在處理幾何的關系過程中,需要正確判斷高階小量并略去,突出主要因素,這是競賽解題中的運算的一項基本要求.
5 總結
基于相位傳播的計算多普勒頻移方法,可以解決一般的多普勒頻移的計算問題. 教師采用幾何方法幫助學生分析信號傳播路徑,計算信號相位傳播的時延,可以幫助降低計算難度,達到數學技巧“降階”,而物理直觀“升階”的目的,提高競賽輔導的實效.

