中小微企業組合貸款的多目標函數線性規劃分析決策研究
(西華大學 電氣與電子信息學院,四川 成都 610039)
首先,通過貸款額度以及信貸利率組成信貸策略,基于因子分析建立了投資風險量化模型。為規避部分風險對行業進行組合貸款,將首先刪除信譽度為D 的123 家企業,留下99 家企業進行行業分類。匯總各行業進銷價稅和營收總額,將進銷項作廢和負票率放入建立的風險量化模型得出不同行業投資風險,以此確定不同行業貸款額度。對于信貸利率,結合數據的流出率,并借鑒宏觀經濟學可持續發展思想,建立多目標函數線性規劃及模型,求解得出最優借貸利率[1]。
然后,通過貝葉斯模型和BP 神經網絡建立信譽度評價模型,擇優選擇貝葉斯模型對其中302 家無信貸記錄的企業做信譽度評價,基于先前建立模型給出信貸策略[2]。
最后,將突發因素選定為新冠病毒疫情,通過《中國金融年鑒2020》判斷出疫情對不同行業影響占比。將占比因素加入投資風險中,再對這302 家企業做信貸額度和信貸利率測評,為促進經濟恢復對測出的利率要適當降低調整[3]。
1 模型假設與約定
1.假設年度信貸總額度為3 千萬;
2.假設題目所給的數據真實可靠;
3.假設在考慮突發因素影響時只有新冠疫情這一因素影響風險量化模型。
2 符號說明及名詞定義
(如表1)
3 模型建立及求解
3.1 數據預處理
收集了如下數據:
1.已知信譽度的123 家企業相關數據;
2.無信貸記錄的302 家企業相關數據;
3.2019年統計銀行貸款年利率與客戶流失率關系(數據來自于歷年中國企業年鑒)。
收集數據給出了企業的所處行業信息、企業交易發票據信息、上下游影響力等相關信息對于眾多企業相關數據,我們需要對數據進行精細整理,使用EXCEL 對數據進行如下處理:
1.首先刪除123家有企業中信譽度為D的企業相關數據;
2.對信譽度為ABC 的企業分別進行進項、銷項價稅匯總并計算營收,進銷作廢率和負票率作為影響因子;
3.對123 家有信貸記錄的,和302 家無信貸記錄的企業進行行業分類;
4.匯總302 家無信貸記錄的企業的進項價、銷項價稅并計算營收,得出作廢率和負票率。
3.2 投資風險量化
3.2.1 投資風險量化模型
1.模型一:因子分析。因子分析方法的基本思想是根據相關性大小把變量分組,使得同組內的變量之間相關性較高,不同組的變量之間相關性較低。信用風險主要與企業實力強弱、供求是否穩定以及信譽度相關。通過對各企業進項、銷項、價稅、合計、營收、進銷作廢率以及負票率這7 個影響因子進行分析風險可得分量化[4]。
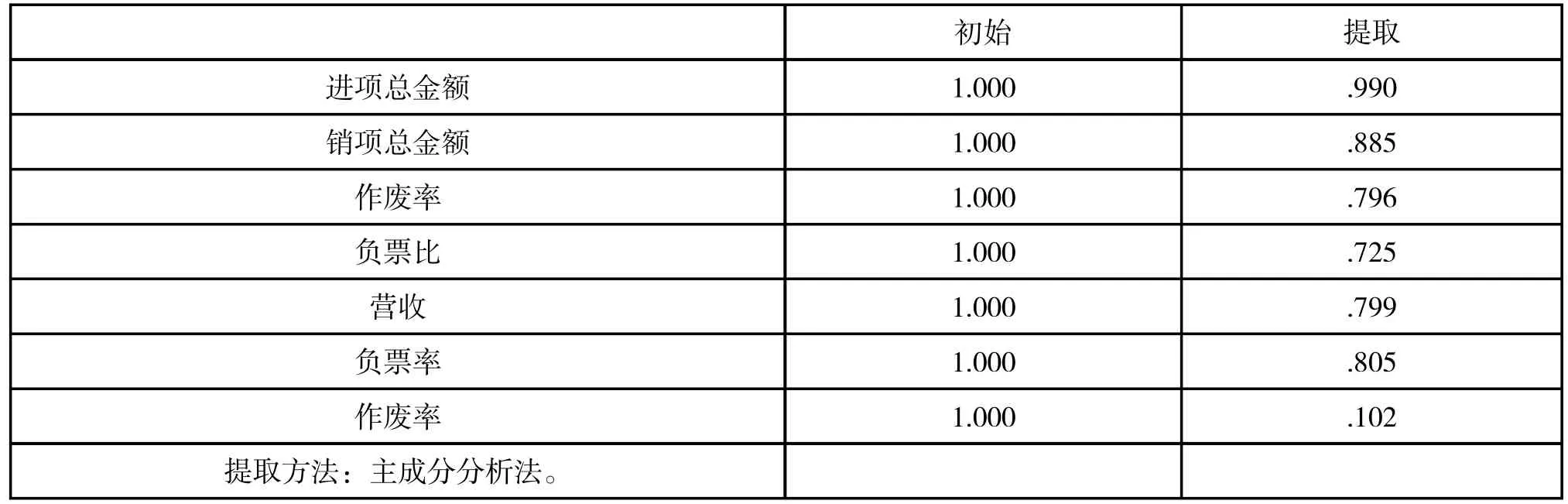
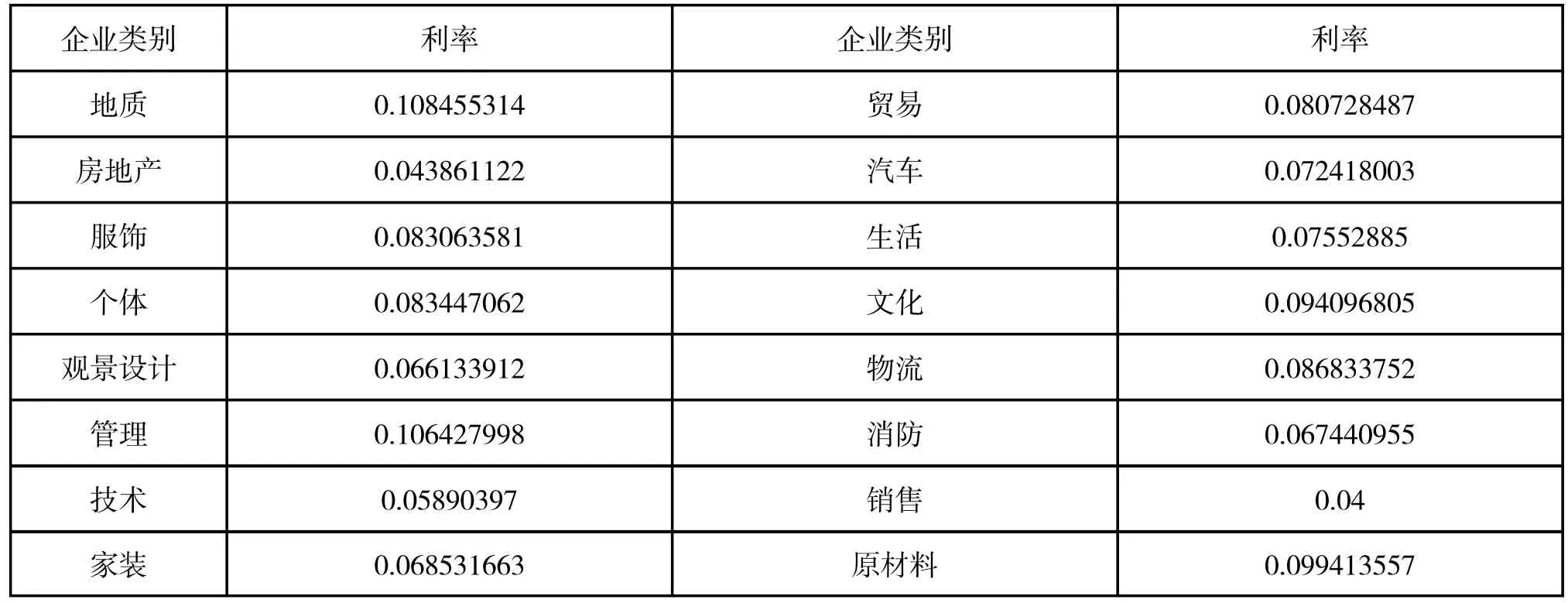
計算步驟:(1)假設原始觀測變量和變化后的新變量均用 x 表示。設原公共因子變量為Y1,Y2,...,Ym,經過標準化后的公共因子變量記為F1,F2,...,Fm(m 表1 符號說明及名詞定義 表2 KMO 和巴特利特檢驗 表3 公因子方差 上述F1,F2,...,Fm稱為主因子,ε1,ε2,...,εm為特殊因子,模型(5)中矩陣Ai=(aij)中的元素aij叫做因子載荷,它代表xi對Fj的依賴程度。 2.因子模型的建立和求解:通過SPSS 對數據進行整理匯總數據進行因子分析試驗。 首先觀測KMO 和巴特利特檢驗結果(表2),可見KMO 達到0.5 以上,滿足因子分析的要求,隨后觀測公因子方差(表3),可見所有數據信息提取比例都達到了80%以上,可見因子分析提取的公因子對變量的解釋性較強。 通過分析看到公因子可分為三個,繪出空間載荷圖,得到因子分系數矩陣方程: 因為單獨使用一種公因子很難具有代表性,因此根據公因子中的方差貢獻率,根據權重綜合得分,再通過三種公因子的得分保存為新變量,得到: 通過此因子分析和分數可得到風險因子。 因為不同行業的公司在投資上具有兩種風險,一種為非系統風險也叫特異性風險,只與個別貸款有關[5],另一種則為系統投資風險,與不同行業的系統風險相關,如果只集中在單個行業則對銀行投資風險與投資質量均有影響。因此,本題采用對不同行業的公司進行分類,并根據收益較高與較低的兩個行業進行組合貸款,以分擔各行業的非系統風險,同時由于數據存在負數對數據進行處理: 表4 各行業安全系數得分 表5 各行業貸款額度 表6 不同企業行業應收利率 因此對各公司整理后,得分情況如表4 所示。 3.2.2 信貸策略模型 1.貸款額度 通過不同行業風險得分對貸款額度做權重分析,得出年度信貸總額為3 千萬的各個行業,可申請貸款額度,表5為各行業具體貸款額度。 2.信貸利率 銀行貸款主要是為了獲得一定收益,即在最大限制下獲得最大的利潤,但高利率會導致客戶流失率上升,從宏觀經濟學角度分析其違背了行業所追求的可持續性發展。因此銀行收益由兩部分組成:一是當前經濟效益較好,信貸利率較高;二是長遠發展,有穩定的客戶來源,企業流失率趨向0。由此將建立一個雙目標的規劃模型,以此兼顧當前利益(較高利率)和長遠發展(較低流失率)[6]。 其目標任務是:(1)合理地配置各行業利率,使得當前的經濟效益S 最大。(2)得出不同利率時不同信譽度的客戶流失率并以此作為參考。配置資源時,兼顧潛在價值,以此求得長遠發展。建立貸款利率可得出不同行業的信貸利率,當前經濟效益值為16 個不同行業組合貸款時最后所交本息金額,即 其中,Si(ai)表示第i 個行業在分得利率ai 時所能創造的銀行收益。 由以上公式得: 另一方面,當該行業認為此利率為可接受時,會給銀行帶來一定的穩定客源,這將關乎銀行的長遠發展。計算得出不同利率對應客戶穩定率,第2 個目標函數為: 隱含約束條件:(1)題目提示。利率應該在一定范圍內: (2)客觀規律。銀行方面總是希望當年經濟收益超過前些年的經濟效益值,由此可以限定: 綜上所述,得到一個雙目標的線性規劃模型: 為了求解該雙目標的規劃模型,必須將其轉化為單目標規劃模型。對二者賦予權重m(0 表6 為當m 取值為0.6 的結果。 此為最優結果,綜上得出銀行對不同行業的貸款策略。 3.3.1 信譽度模型 1.模型一:BP 模型 BP 神經網絡是一種分層型的典型多層網絡,具有輸入層、隱含層和輸出層,層與層之間多采用全連接方式,其中輸入層和輸出層都為一層,而隱含層可以是一個或者多個,但是僅含有一個隱含層時,網絡就能夠滿足大多數的實際需求,能夠很好地解決問題,且提高算法運行效率。 (1)該模型由每組數據的各項影響指標作為輸入,以所得信譽度值作為輸出,所以樣本有7 個輸入參數,1 個輸出參數,這里的隱藏層通過公式計算得出n2 取值為15,即設置神經網絡結構為7-15-1,即輸入層有7 個節點,隱藏層有15 個節點,輸出層有1 個節點。 其中,n1 為輸入層神經元個數,n2 為隱藏層神經元個數。 (2)步驟 步驟1:初始化BP 神經網絡模型。設置網絡的初始權值和閾值,設置網絡的最大訓練次數與誤差條件,給隱層輸出層賦初值15。 步驟2:正向傳播求輸出函數。從輸入層開始,輸入值乘以對應的權值,加上其對應的偏值,最后通過激勵函數得到各個神經元的輸出值。計算公式為: (22)式中:Wij為權值;Oi為輸入值;Bj為閾值;Oj為輸出值。 步驟3:誤差反向傳播。通過反向傳播可以計算出輸出值,輸出值與真實值之間會存在1 個誤差,誤差函數可以表示為: (23)式中:Tj為真實值;Oj為輸出值。 計算每層神經元的等效誤差,從輸出層開始,計算到輸入層,不斷重復步驟2 和步驟3 的過程,以確保所有訓練樣本都進行了計算。 步驟4:更新各層的連接權值與閾值。通過式(24)計算出最后一層誤差,將該誤差利用梯度下降法進行反向傳播,經過隱含層直到最上一層,從而對權值和閾值進行更新。計算公式為: 式中:Wi為權值更j`新量;Bj`為閾值更新量;l為學習率,取值范圍為(0,1)。 步驟5:確定迭代條件。返回到步驟2,根據剛計算得到的權值和閾值,計算正向傳播輸出值,直到輸出值與真實值之間的差值滿足精度要求和網絡訓練完成為止,反之則繼續迭代更新權值和閾值,直到滿足要求為止。 其中,p=1,2…a;l=1,2…m;E 為給定的精度要求值。 步驟6:測試與誤差分析。將歸一化后的測試集代入訓練后的BP 神經網絡,得到測試結果,進行反歸一化處理,將結果與真實數據比較,進行誤差分析。 2.模型二:貝葉斯 設G1、G2為兩個p 維總體,概率密度分別為f1(x)和f2(x),總體G1、G2的先驗概率分別為q1和q2,誤判損失分別為C(2|1)和C(1|2),判別準則記為R=(R1,R2):若樣品x ∈R,則x ∈G1,否則X ∈G2。 在準則R=(R1,R2)下的誤判概率為: 表7 分類函數系數 表8 特征值 表9 得分結果 經花費三個小時得到結果,這主要由于它較低的學習效率;(2)由于對于激活函數的依賴導致它在激活函數達到飽和時網絡的自我調節幾乎停止;(3)容易陷入局部最優解。由于其本身的不完備性,采用的梯度下降法讓最優值向著最初的方向下跌。 貝葉斯判別法:(1)相比于BP 算法,貝葉斯判別法的速度較快,并且簡單有效;(2)對于分類問題也同樣特別有效,其復雜性同樣沒有明顯的上升。 同樣它也具有相應的缺點:(1)對于組內預測它沒有較好的判別性能,容易使判別結果趨于固定值;(2)沒有較好的理論基礎進行支撐。 考慮到本次數據較少沒有較大的數據流作為支撐,并且也沒較好的平臺能很好的運行BP 算法。作為最致命的問題,在本題中它陷入了局部最優解的狀態,因此選擇了貝葉斯判別法作為對企業信譽度的判斷。 根據模型一 中完善信譽度后的數據,得出302 家企業中不同行業的風險得分,由此帶入信貸策略模型,得出在年度信貸總額為1 億時對不同行業進行組合貸款的信貸策略。 考慮到突發因素(新冠病毒疫情)對不同行業的影響:由于對突發因素并沒有較為準確的定義,想要根據給出的財務信息得出其在疫情中的狀況幾乎不可能,所以要將企業的行業進行分組。查閱中國銀行于今年出版的《中國金融年檢》,將受影響的等級分為四級:非常嚴重、較為嚴重、嚴重、輕微,并且對于不同行業影響有: 非常嚴重:服飾、個體、物流、園藝、家裝、銷售; 較為嚴重:管理、建筑; 嚴重:汽車、食品、技術、文化; 輕微:環保、醫療、原材料、法務。 最后通過對比往年這時候的銷售數據可得到如下影響:非常嚴重:44.7%;較為嚴重:20%;嚴重:10%;輕微:8%。其受到的影響全部作用在風險量化上后的得分情況如表9 所示。 1.建立了基于因子分析的量化評價指標,以此對投資風險進行量化。為減小且規避部分投資風險進行了組合貸款。并建立了多目標線性規劃函數,考慮當前經濟效益和長遠發展,加入約束條件計算得出不同行業的利率,從結果分析可以得出對從事銷售、房地產和技術行業的風險較低,相應的所給利率也低,但貸款額度較高。 2.建立了信譽度模型。通過貝葉斯判別測得對302 家企業的行業分類的信譽度,再基于先前建立信貸策略模型得出不同行業對應貸款額度以及貸款利率。 3.面對突發因素。如新冠病毒疫情對不同行業的打擊,其中從事服飾、個體經營和物流的企業受到的打擊較大。為促進疫情過后的經濟恢復將放寬信貸政策,通過降低基利率刺激企業貸款,此時最終貸款利率為4%~13,6%。 本文所使用的因子分析模型通過適當的簡化使原始變量的信息進行重新組合,可找出影響變量的共同分子,化簡了數據。同時采用的貝葉斯判別法計算簡單,且不涉及各總體的分布,因此適用性很廣。 由于缺少相關數據,我們對問題的分析存在局限性,同時我們運用因子分析在計算因子得分時,采用的是最小二乘法,此法有時可能會失效,不適合用到一些研究中。采用的貝葉斯判別法未考慮各個總體出現的概率大小,且未考慮到誤判后造成的損失。 可以對不同行業、不同類別的公司的信貸策略做更為細致的研究,可以增加不同突發因素,研究其對信貸模型的影響。 可以結合模型一、模型二建立的可靠數據,較為準確的分析中小微企業的實力和信譽對信貸風險影響,然后銀行依據信貸政策、企業的交易票據信息和上下游企業的影響力等因素提出合理的信貸策略,使其發揮更大的效益。



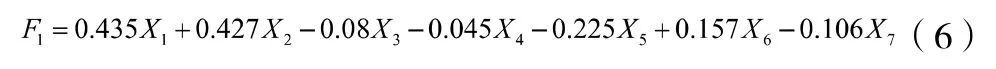
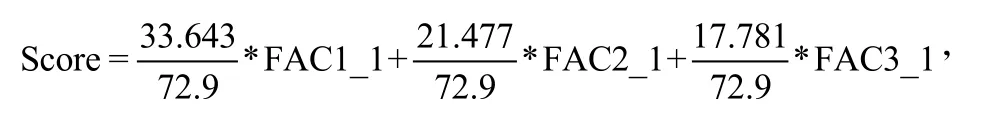


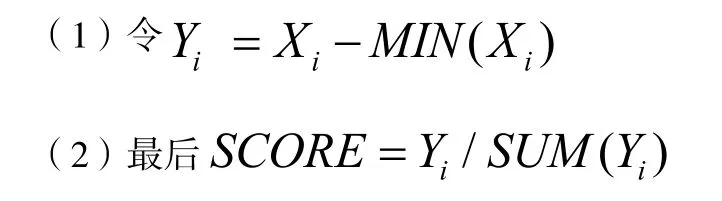

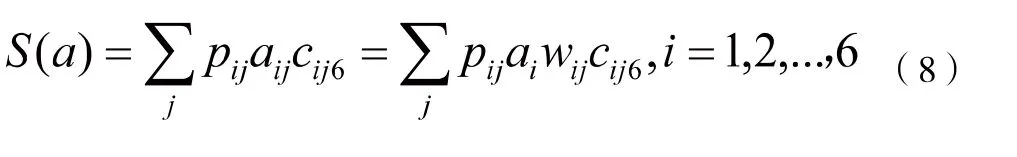
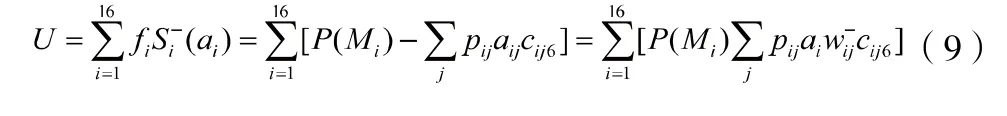

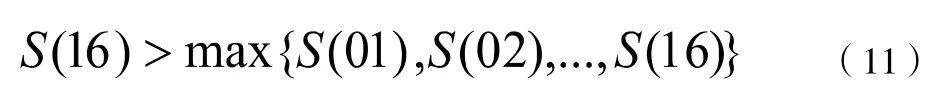
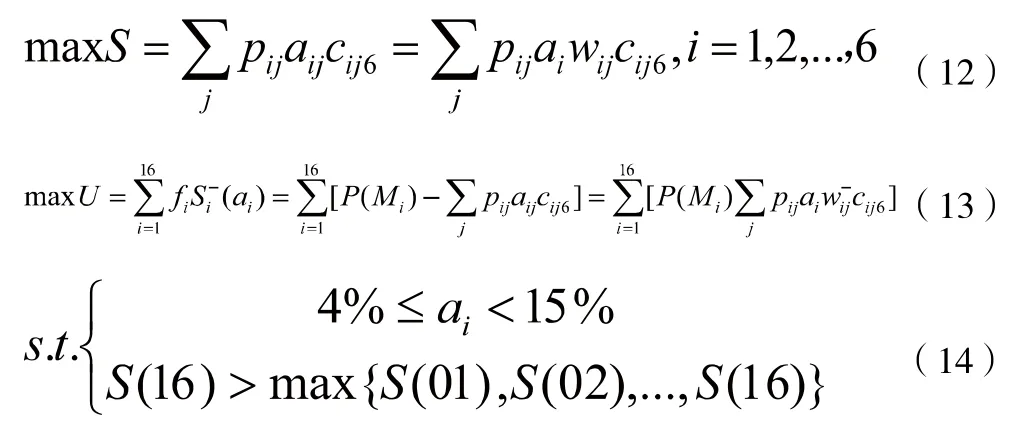
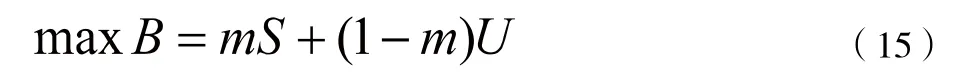
3.3 貸款模型及求解

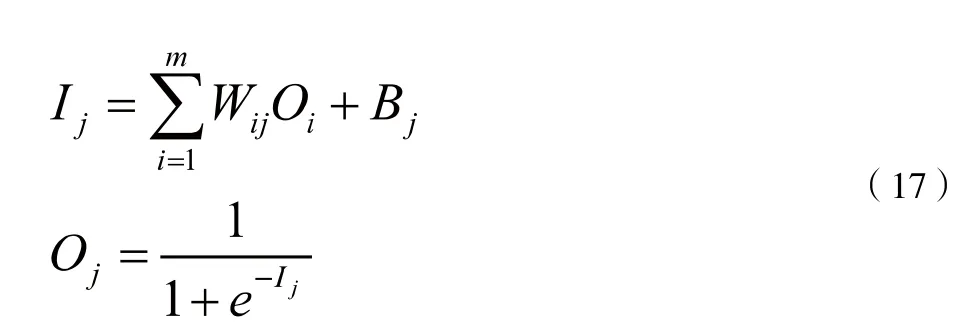
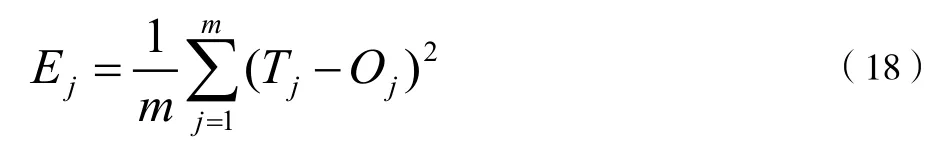
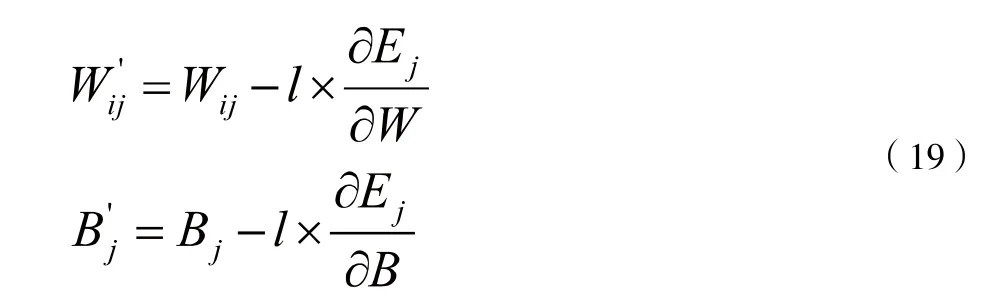

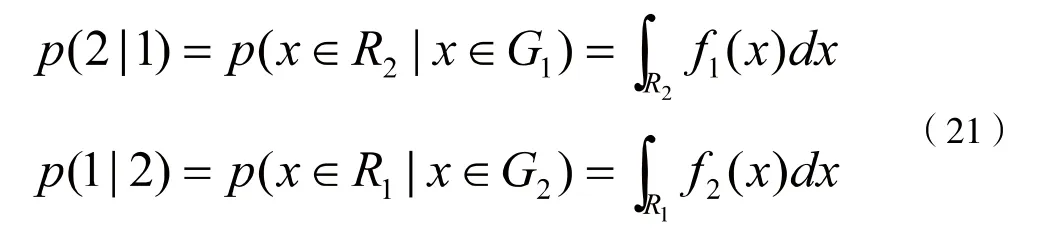





3.4 其他因素對貸款風險的模型及求解
4 結果分析
5 模型評價
5.1 優點
5.2 缺點
5.3 改進方法
6 模型推廣

