基于Mindlin解的盾構隧道施工地表變形及參數敏感性分析

楊玉平,劉運思,牟天光,李小雷,屈軍平,周小龍,王晶,周國民

(1.中鐵北京局集團 (天津)工程有限公司,天津,300000;2.湖南科技大學 巖土工程穩定控制與健康監測省重點實驗室,湖南 湘潭,411201;3.湖南科技大學 土木工程學院,湖南 湘潭,411201)

近年來,隨著國家經濟的日益發展,城市人口不斷增長,市內交通擁堵現象嚴重,而城市可利用交通建設的土地有限。因此,地下空間的利用日趨重要,地鐵建設是緩解市內交通擁堵的方法之一。然而,地鐵隧道周邊建筑物密集或位于道路下方,對控制地表變形要求較高,尤其在不良地質地區,隧道施工過程中,地表容易出現隆起或下沉,甚至會造成地面坍塌,這就跟給現場盾構施工帶來極大的風險。縱向地表變形規律是盾構隧道掌子面前后土體空間約束效應的直觀反映,預示著掌子面的穩定,以及盾構機推進過程中圍巖的穩定情況。因此,開展盾構施工縱向地表變形特征的研究具有極其重要的意義。目前,國內外一些學者對盾構隧道施工地層變形進行了相關的研究,如呂璽琳等[1]和黎春林等[2]對地鐵盾構隧道施工過程掌子面穩定和土體擾動情況進行數值模擬,考慮了壁后注漿參數、土體的塑性區等因素,但是沒考慮盾殼外壁與圍巖之間的摩擦力引起的土體變形。顏波等[3]、葉飛等[4]和何川等[5]對影響盾構法隧道施工引起地層變形的土層參數做了相關研究,得出控制地表沉降的措施,但未揭露縱向地表變形的規律。程紅戰等[6]和王長虹等[7]考慮巖土參數空間隨機性在盾構施工地表沉降的影響,進行了相關的理論分析,得出地表沉降近似服從對數正態分布,但未考慮盾構推進過程中開挖倉壓力對地表變形的影響。Mindlin[8]提出彈性體在力的作用下空間某一點的變形的理論計算方法。MIRO等[9]和MOLLON等[10]考慮地層參數隨機性對地表變形影響進行了概率統計分析。部分學者[11-16]利用peak公式,通過大量的工程監測資料進行分析,得出盾構隧道地表變形的彈性解。

綜上所述,本文基于Mindlin解,引入摩擦角φ,推導了盾構施工過程縱向地表變形的彈塑性解析解,開展盾構施工過程縱向地表變形規律研究,獲得盾構施工隧道中線上方縱向地表變形特征,以及地層參數對縱向地表變形的影響,為盾構施工前進行風險預測及地表變形對周邊構筑物的影響提供參考。

1 基于Mindlin解盾構施工縱向地表變形理論分析

1.1 盾構施工中地表變形分析

根據彈性力學R.Mindlin解,當土層為均質各向同性半無限彈性體,則在距表面某一深度H點作用有水平集中力P時的任意一點(x,y,z)的豎向位移可采用Mindlin解。水平力作用下地層豎向變形簡圖如圖1所示。假設本模型土層為均質各向同性半無限彈塑性體,土體的變形是由于土顆粒間的位置發生變化,這樣土層的變形表現為非線性,彈塑性土體的變形與其抗剪強度有關,而內摩擦角是土體抗剪強度的重要參數,因此可假設彈塑性土體的變形與其內摩擦角的正切值存在聯系,基于Mindlin解,對彈塑性土體在水平均布荷載作用下對地表產生的位移進行積分,得到水平均布荷載作用時,隧道中心線上方縱向地表任意一點的豎向位移。本模型假定盾構施工在模擬計算的里程范圍內沿直線推進,不考慮盾構施工糾偏、調線調坡、管片變形等引起的地層損失。

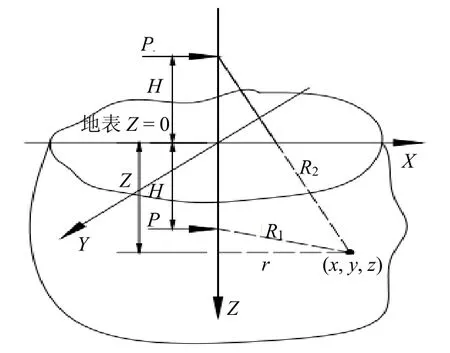
圖1 水平力作用豎向地層變形簡圖

2.2 掌子面附加作用應力引起的地表豎向變形

假定盾構機推進過程在隧道掌子面施加的開挖倉壓力為圓形均布荷載P(kPa),掌子面側向靜止土壓力為F(kPa),得到施加在掌子面的附加作用應力(現場施工時ΔP一般控制在±20 kPa,本文取附加作用應力為20 kPa。基于Mindlin解,取掌子面均布荷載微元作用引起的地表某一點的豎向位移為dz,對掌子面區域的均布荷載作用引起的地表豎向位移進行積分,得到隧道中心線上方由掌子面附加作用應力引起的地表豎向位移變形量z1。

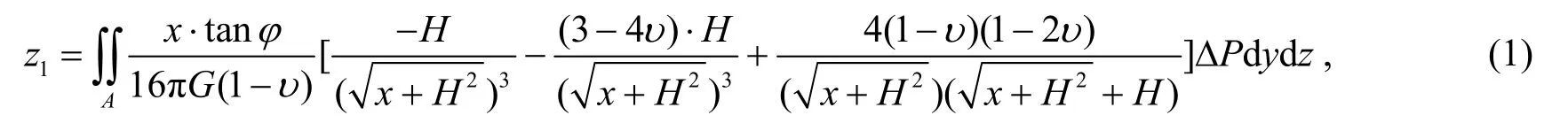
式中：z1為隧道中心線上方某一點的地表位移變形量,H為均布荷載作用的重心到地表X軸的距離,G為土體剪切彈性模量,,E為變形模量,υ為泊松比,?為內摩擦角,A為隧道掌子面面積,(x,y,z)為所求位移點的坐標。

2.3 盾殼外圓周側壁與隧道圍巖之間的摩擦力作用引起的地表豎向變形

取盾構機外圓周側壁外表面的微元面積Rdθdl,基于Mindlin解,對盾構機外側面圓周摩擦力的作用引起的地表豎向變形進行積分得到盾構機外壁與圍巖之間的摩擦力引起的地面豎向變形計算公式為

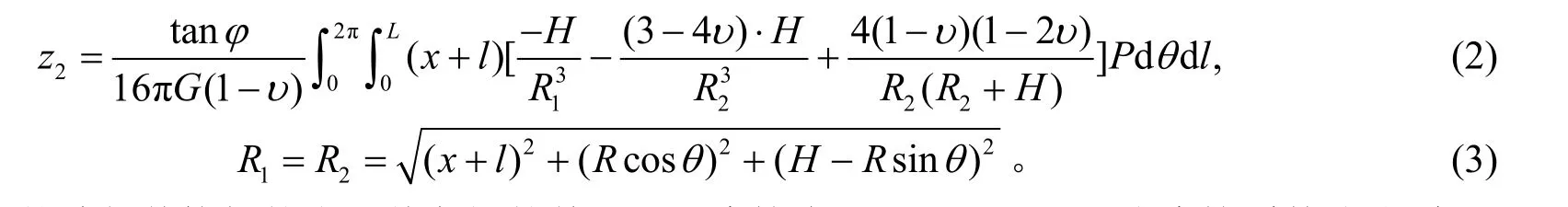
式中：P為盾構機外壁與其接觸的巖土體之間的單位面積摩擦力(kPa),P=μFN,μ為摩擦系數(根據本區間地質資料圓礫層摩擦系數取0.5),FN為圍巖對盾殼外壁法向壓應力,R為盾構機外徑,L為盾構機長度。

2.4 盾構施工引起的地表最終豎向變形

將掌子面附加作用應力作用效果和盾殼外壁與圍巖土體之間的摩擦力作用效果疊加得到最終隧道軸線上方地表豎向變形。

3 工程實例

本模型工程依托南寧地鐵某區間右線典型里程區間,本段區間隧道為兩條單洞單線圓形盾構隧道,右線隧道先于左線隧道施工,線間距為14.0 m,覆土埋深15 m。隧道位于⑤1-1圓礫地層,地面高程為76.5 m,地下水位穩定常水位高程為68.29 m。其物理力學參數詳見表1。

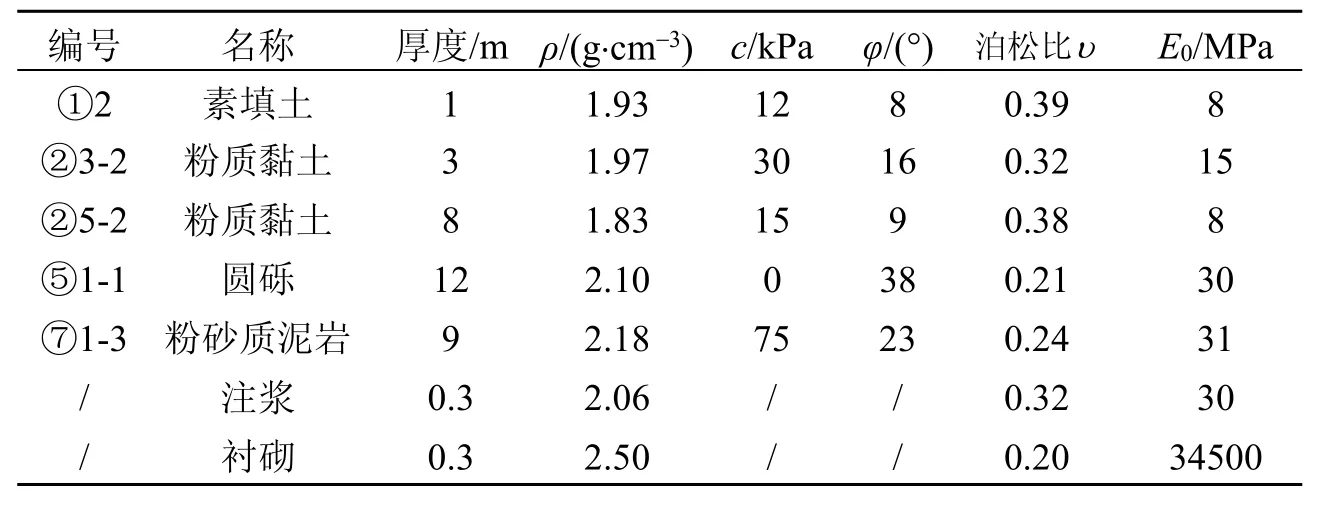
表1 物理力學參數表

3.1 數值分析方法

本文依托南寧地鐵某區間右線隧道典型里程地質進行數值分析,隧道盾構施工過程采用FLAC3D軟件分析,計算模型選取縱向(Y向)長度60 m,橫向(X向)寬度取為56 m,下邊界取2倍洞涇即12 m,隧道埋深15 m,即建立長×寬×高(60 m×56 m×33 m)計算模型。盾構機模擬外徑為6.24 m,長度7.7 m,隧道外徑為6 m,內徑為5.4 m,隧道襯砌采用環寬1.5 m,厚度為0.3 m的鋼筋砼管片,注漿層厚度取為30 cm。本文地層采用Mohr-Coulomb本構模型,隧道襯砌、壁后同步注漿層采用的則是彈性模型,注漿過程模擬則采用等代層的形式模擬注漿層。數值模擬網絡示意圖見圖2所示。

隧道縱向長度60 m,盾構施工從y=0開始推進,每次開挖4環即6 m,分5步開挖到y=30 m斷面,監測得到開挖面前方及后方的地表變形值。具體操作如下：

開挖前,需構建地層的初始應力場。土層在原始自重應力作用下應力達到平衡,然后將土層位移清零,邊界約束的速度設為零。

開挖后首先隧道縱向開挖范圍0～6 m。開挖模擬為瞬時開挖,掌子面從0 m瞬時達到6 m,并在掌子面施加均布荷載模擬開挖倉壓力。在等代層施加均布荷載來模擬盾殼與圍巖之間摩擦力。

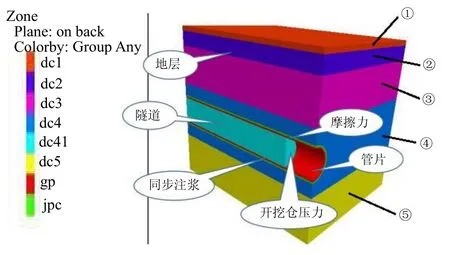
圖2 數值模擬網格示意圖

重復以上操作,依次進行下一步開挖,直到掌子面開挖到達y=30 m斷面。

3.2 盾構施工過程中縱向地表變形計算分析

圖3所示為盾構隧道中心線上方的縱向地表變形曲線。由圖3可知,盾構隧道開挖過程中,隧道中心線上方縱向地表變形規律基本呈現為“S”型,盾構施工過程中,開挖倉壓力會大于或等于掌子面水平土壓力,掌子面前方土層還受到來自盾殼與圍巖之間向前的摩擦力作用,帶動其周圍土體顆粒向前移動,應力狀態的改變會引起土體的變形,掌子面前方土體受到擠壓而隆起,掌子面后方土體存在松散空隙而沉降,隨著能量的傳播和耗散,掌子面前后方沿著縱向距離方向地表變形量先增加達到某一個波峰而后減小。實測數據、數值分析和理論計算所得數據較吻合,但掌子面后方理論計算所得的沉降量較數值分析和實測數據值小,導致這一原因是理論計算未考慮隧道開挖完成后地層損失及襯砌管片的變形量。

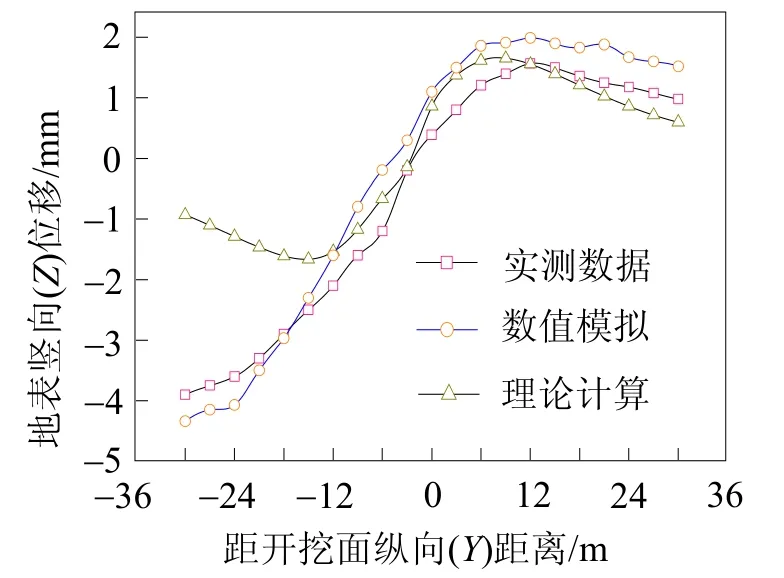
圖3 縱向地表變形對比分析圖

4 各參數對縱向地表變形敏感性分析

4.1 開挖倉壓力對縱向地表變形的影響

盾構施工的一個重要掘進參數在于控制開挖倉壓力與隧道掌子面水土壓力的平衡。盾構機開挖倉壓力是否準確,直接影響著開挖面的穩定和地層的變形。開挖倉壓力與朗肯理論計算的掌子面側向靜止土壓力的比值,記為RP。本文選取RP=1、1.2、1.4進行對比分析,如圖4所示。由圖4可知,增加開挖倉壓力對地表縱向變形的影響較小,當開挖倉壓力增加20%,地表縱向變形增加約5%。地表縱向變形主要還是由盾殼外壁與圍巖之間的摩擦力引起。

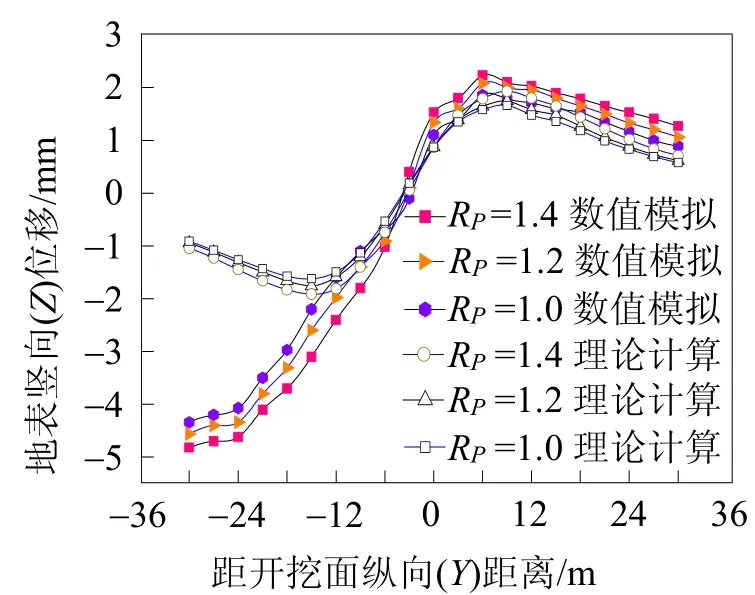
圖4 不同RP值縱向地表變形圖

4.2 盾殼摩擦力對縱向地表變形的影響

當隧道處于不同的土層時摩擦系數會不一樣,根據本區間地質資料,粉細砂層μ為0.4,粉質粘土層μ為0.3,圓礫層μ為0.5,假定在同一埋深盾殼外壁的法向應力一樣,從而不同摩擦系數可得到不同的摩擦力。圖5所示為不同摩擦系數縱向地表變形曲線。由圖5可知,理論計算和數值模擬均可得出盾殼摩擦力與縱向地表變形之間存在著正相關的關系,但并非線性關系,盾構機側壁與圍巖之間形成的摩擦力越大,隧道上方縱向地表變形也越大,盾殼側壁摩擦力對縱向地表變形影響較大。當摩擦力增加30%,縱向地表變形量增加最大約35%。

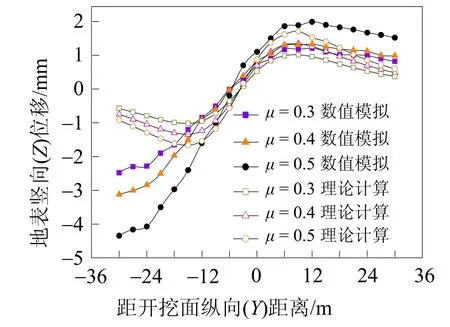
圖5 不同摩擦系數縱向地表變形圖

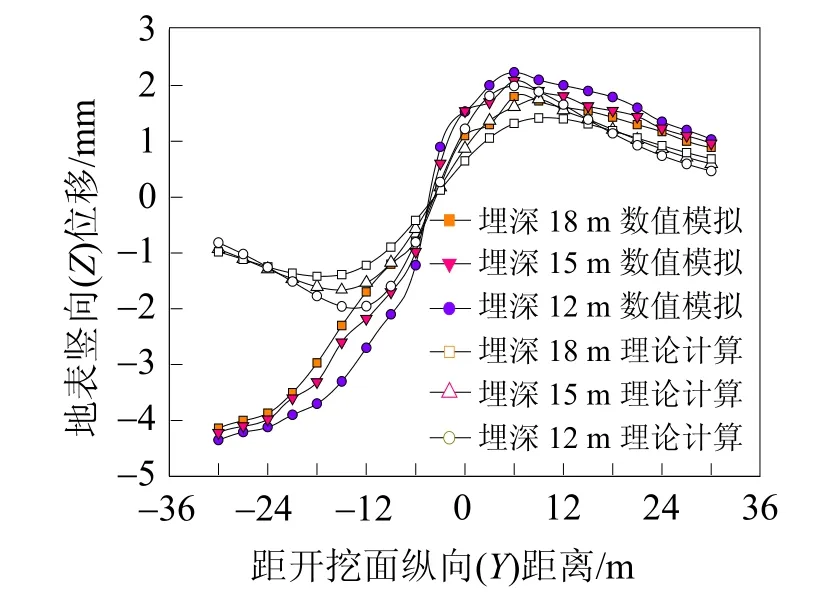
圖6 不同埋深縱向地表變形圖

4.3 不同埋深對縱向地表變形影響

城市地鐵盾構隧道在車站的端頭埋深較淺,隧道離開車站后,根據線路的調整,埋深會增加,而在相鄰里程范圍內地層條件相差不大,隧道埋深的不同,盾構開挖后的圍巖應力分布就不一樣,縱向地表變形也就不一樣。圖6所示為不同埋深縱向地表變形圖。由圖6可知,不同埋深下盾構隧道縱向地表變形規律,同一地層中,隧道埋深的不同,縱向地表變形量也不一樣,且隧道的埋深對縱向地表變形量的影響較為顯著。在開挖面附近前后25 m范圍內縱向地表變形隨著隧道埋深減小而增大比較明顯,當埋深減小20%,縱向地表變形增加約18%。在掌子面前方超過30 m范圍后的縱向地表變形對隧道的埋深的敏感性較小。

4.4 不同變形模量和泊松比對縱向地表變形影響

盾構位于不同地層,其彈性模量和泊松比不同。為了研究彈性參數對縱向地表變形的影響,本文對不同彈性參數展開研究。圖7所示為不同變形模量和泊松比縱向地表變形曲線圖。由圖7可知,隨著土層的變形模量減小、泊松比增大,縱向地表變形量增加,當泊松比增加20%,變形模量減小25%,縱向地表變形量增加最大約為50%,土層的變形模量和泊松比的變化對縱向地表變形量的影響較為顯著。

4.5 地表變形對土層內摩擦角φ的敏感性

盾構機推進過程將改變隧道周邊土層的應力—應變狀態,土體的內摩擦角是土的抗剪強度的重要參數,影響著土層的變形量。圖8所示為不同內摩擦角縱向地表變形曲線圖。由圖8可知,隨著土體內摩擦角的增大,縱向地表變形也增大,且影響較為顯著,但地表縱向變形增加幅度有所減緩;當內摩擦角從15°增加到25°,增量66.7%,縱向地表變形顯著增大,增加量最大約為73.1%,當內摩擦角超過25°后,隨著內摩擦角的增大,縱向地表變形量也增大,但是增量幅度減小,證明內摩擦角超過25°后,縱向地表變形對內摩擦角的敏感性減弱。

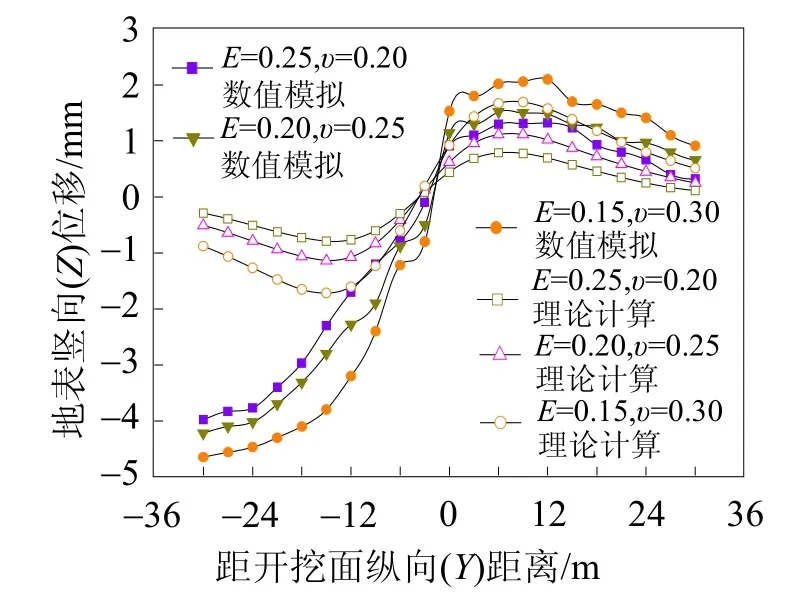
圖7 不同變形模量和泊松比縱向地表變形圖

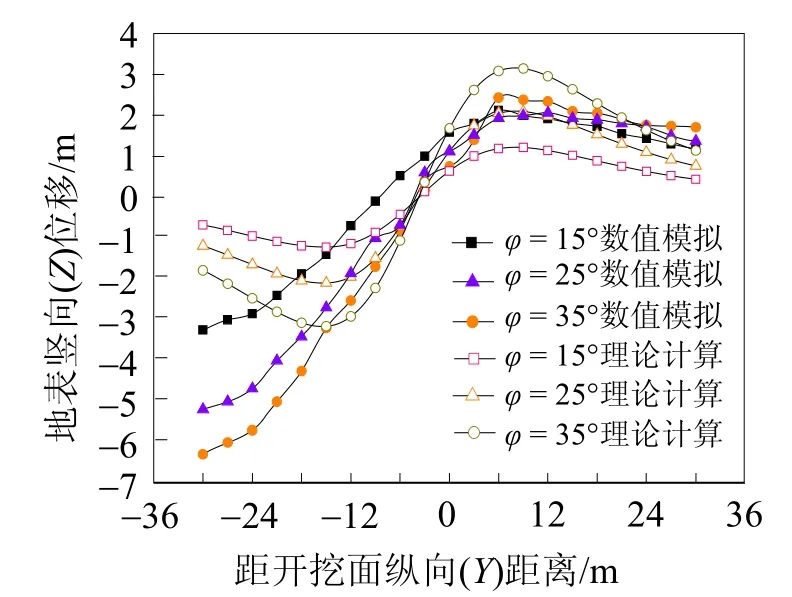
圖8 不同內摩擦角縱向地表變形圖

5 結論

本文基于Mindlin解,引入摩擦角φ,推導了盾構施工過程中縱向地表變形計算公式,并結合實際工程,與數值分析和監測數據進行對比分析,得到以下結論：

(1)基于Mindlin解,引入了摩擦角,推導了盾構施工縱向地表變形的彈塑性解,與數值分析和實測數據較吻合;

(2)盾構施工過程中,隧道中線上方縱向地表變形規律呈現為S型,掌子面前方地表隆起,掌子面后方地表下沉;

(3)盾殼與圍巖之間的摩擦力、土體內摩擦角?與盾構隧道中線上方縱向地表變形存在正相關,盾殼摩擦力增加30%,縱向地表變形量增加最大約35%;內摩擦角增加66.7%,縱向地表變形量最大約為73.1%;當泊松比增加20%,變形模量減小25%,縱向地表變形量增加最大約為50%;開挖倉壓力增加20%,縱向地表變形增加約5%;同土層不同埋深,當埋深減小20%,縱向地表變形增加約18%。