分區最大化色域邊界描述器的空區插值算法

朱 明，趙興運

河南工程學院，鄭州450007

1 引言

在跨媒體圖像復制中，需要把圖像顏色從源設備色域映射到目標設備色域內。能否精確地描述圖像和設備的色域邊界直接影響著色域映射精度的高低[1-3]。在圖像復制領域中，當前有兩種應用較為廣泛的色域邊界描述器。第一種是基于凸殼“充放氣”的色域邊界描述算法[4-6]。該方法首先對顏色樣本數據進行非線性變換，使得變換后的數據更接近凸集，然后進行凸殼計算，獲得色域邊界。凸殼算法需要將顏色樣本點進行包扎，計算量較大，而且需要提前對色域形狀作出假設。對于設備色域的計算來說，作出此假設非常有效。但對于圖像色域來說，由于凸殼性并非圖像色域的屬性，因此該算法不能很好地描述非凸色域邊界，可能會影響某些圖像的色域邊界計算精度。

針對凸殼算法存在的問題，Morovi? J 和Luo M R又設計了分區最大化色域邊界描述器（Segment Maxima Gamut Boundary Descriptor，SMGBD）[7-8]。該方法先根據明度軸和色調角將CIELAB 顏色空間按照球坐標進行區域等分，并將分割后的子區域內具有最大球坐標半徑的顏色樣本點進行存儲，最后根據子區域的鄰接關系把各分區的顏色樣本點進行連接，以獲得色域邊界。SMGBD無需對色域形狀作出預先假設，因此該方法對于設備和圖像色域均有較好的描述效果。更重要的是，區域分割法還提供了線色域邊界（Line Gamut Boundary，LGB）的計算方法，可以方便地應用于色域映射。

憑借上述優點，SMGBD 成為目前應用較為廣泛的色域邊界描述器。但該方法在提出時仍存在一些問題：（1）由于不同圖像的顏色分布特征不同，因此在計算圖像色域邊界時，可能會出現許多分區缺失邊界點的情況。這就需要對缺失邊界點的分區進行插值，否則會嚴重影響圖像色域邊界的描述精度。（2）在空區插值后，針對相鄰分區邊界點連線與等色相面的重合所導致的線色域邊界計算問題，也需要設計出合理的解決方案。本文在深入分析SMGBD的基礎上，提出了一種基于相鄰分區加權平均的空缺分區插值算法，并在此基礎上研究了線色域邊界的計算以及對異常問題的處理。借助色域映射的方式，本文設計了心理物理學實驗來評價色域空區插值算法的效果，同時還測試了算法的計算效率。

2 基于相鄰分區加權平均的色域空區插值算法

2.1 插值算法的設計原理

圖1顯示了SMGBD對CIELAB球體顏色空間的6×6區域分割情況，圖中標識的分區即為一個邊界點空缺分區。先將空缺分區的邊界點位置確定在該分區的中心，在已知分區數量的情況下，可以很容易地求出該空缺分區邊界點的球坐標角度α 和θ；然后再利用鄰域加權平均法插值計算出該分區邊界點的球坐標半徑r ：即以空缺分區為中心，分別沿圖2 所示的搜索路徑（向上，下，順時針，逆時針方向）查找相鄰分區的邊界點。可以明顯看出：該插值搜索算法的基本原理是對各方向的鄰域由近及遠逐一搜索（若當前分區為空，則按箭頭所指路徑搜索下一分區，直到在這一方向上找到非空分區為止），這樣才能確保最終得到的插值鄰域為該方向距離中心最近的非空分區。搜索完成后，將各鄰域分區邊界點對應的球坐標半徑r 進行加權平均，各相鄰分區對應的權重值與其和中心空區的距離成反比。需要注意：插值計算完成后，需要根據插值邊界點的球坐標半徑r 再計算出邊界點的明度值，并判斷該值是否超出明度L*軸的范圍[0，100]，若超出范圍，則需要進行數據規范化處理。

圖1 CIELAB球體顏色空間的區域分割情況（6×6分區）

圖2 插值算法的搜索路徑（從空缺分區向四個方向的相鄰分區）

2.2 線色域邊界的計算及異常問題的處理

空區插值完成后，針對色域映射的具體應用，還需要計算每個待映射顏色在等色相面內的線色域邊界（LGB）。圖3 顯示了線色域邊界的計算原理：首先在CIELAB球坐標系的水平方向上，逐行判斷待映射顏色所處的等色相角平面的左右相鄰分區，然后依次連接左右相鄰兩個分區的邊界點，這些連線與等色相面的交點為線色域邊界的節點（LGB Points），最后從上到下將這些節點連接起來形成線色域邊界。求解LGB點的本質是求解左右兩分區連線方程與等色相角平面方程所構成的線性方程組。

假定該等色相角平面在某行左右兩個相鄰分區的邊界點為J(j1,j2,j3)和K(k1,k2,k3)，那么連接兩點的直線方程可表示為式（1），其中P(p1,p2,p3)為該直線上任意一點，矢量u(k1-j1,k2-j2,k3-j3)固定不變，t 為可變參數。由于色相角已知，假定該等色相角平面過明度軸上已知兩點M(m1,m2,m3),N(n1,n2,n3)和已知的待映射顏色點L(l1,l2,l3)，因此該平面方程可表示為式（2），其中Q(q1,q2,q3)為該平面上任意一點，矢量v,w 固定不變，r 和s 為可變參數。

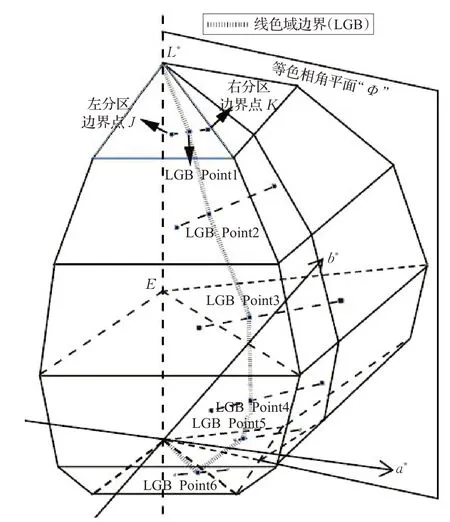
圖3 線色域邊界的計算原理

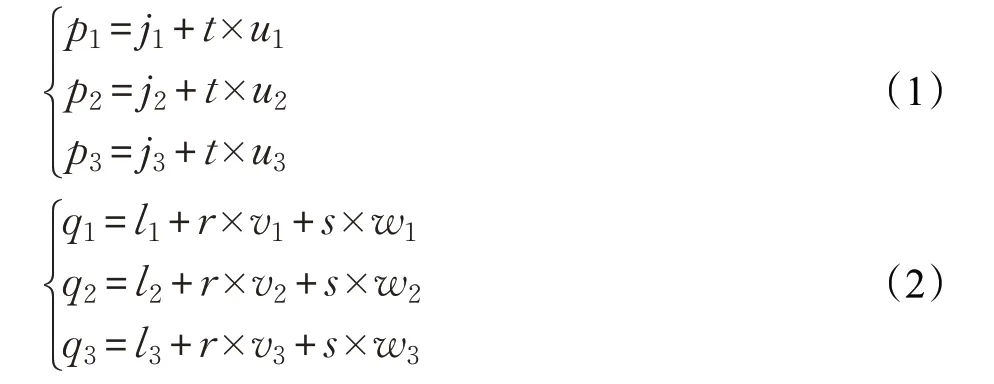
為了得到相鄰分區邊界點連線與等色相面的交點，可將式（1）和（2）構成線性非齊次方程組（3），其中r,s,t為待求解變量。當系數矩陣與增廣矩陣的秩相等，且都為3時，該方程組有唯一解，即為連線與平面的交點，此為大多數情況；但還需要注意另外兩種特殊情況：（1）當系數矩陣與增廣矩陣的秩相等，但小于3 時，該方程組有無窮解，此時說明該連線可能位于等色相面內；（2）當系數矩陣與增廣矩陣的秩不相等，該方程組無解，此時說明該連線可能與等色相面平行，因此無交點。注意：在實際應用中，第二種情況是不會發生的。當第一種情況發生時，本文采用了一種簡單而又合理的處理方式：令t=0，此時由式（1）可知，p1=j1,p2=j2,p3=j3，這意味著相鄰分區連線與等色相面的交點被設定成其中一個分區的色域邊界點，這樣可以避免線色域邊界和色域映射計算中出現的色域邊界缺失問題。

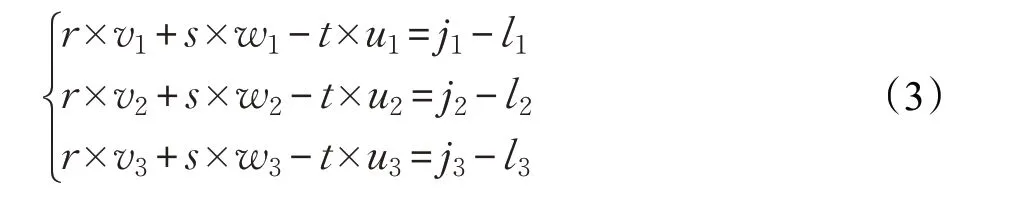
2.3 方法分析

當使用SMGBD 和空區插值算法（6×6 分區）計算圖4所示測試圖像的色域邊界時，所得的各分區色域邊界點構成了色域邊界描述矩陣（GBD_Matrix，GRD 矩陣），矩陣中各元素的CIELAB 值如表1 所示，表中的6行6列數據分別對應6×6的SMBGD分區。對于CIELAB值為（70.196，0，14.000）的某個圖像像素來說，它處在色相角α 為90°的等色相面內。根據表中數據可知，該等色相面第1行（頂部）左右相鄰分區邊界點的CIELAB值分別為（100，0，0）和（99.2，-5，27），兩點的色相角分別為0°和100°，因此其連線與90°等色相面的交點只有一個，即其中一個邊界點本身。這時，從表2可以看出：前兩個LGB點具有相同的CIELAB色度值，因此是互為重合的一個點。注意：在該案例中共有8 個LGB 點，分別對應垂直方向上6 個分區的LGB 點和明度軸的上下兩個端點。

圖4 原始圖像及映射像素

另外，該等色相面第6行（底部）左右相鄰分區邊界點的CIELAB 值分別為（0，0，0）和（1.2，0，2），其對應的色相角分別是0°和90°，此時可以明顯看出：這兩個分區邊界點連線與90°等色相面完全重合，即與上述第一種特殊情況對應。通過求解方程組（3）可知，系數矩陣與增廣矩陣的秩相等，但都等于2（小于3），即有無窮解。這時利用本文的解決方案，令t 值為0，此時交點計算結果為其中一個邊界點本身（CIELAB：0，0，0）。從表2可以看出：后兩個LGB 點互相重合成了一個點。與計算設備色域所用的均勻采樣色標不同，彩色圖像的顏色分布較不規則，因此上述情況經常在計算圖像色域時發生，且通常發生在LGB線色域邊界的頂部或底部。

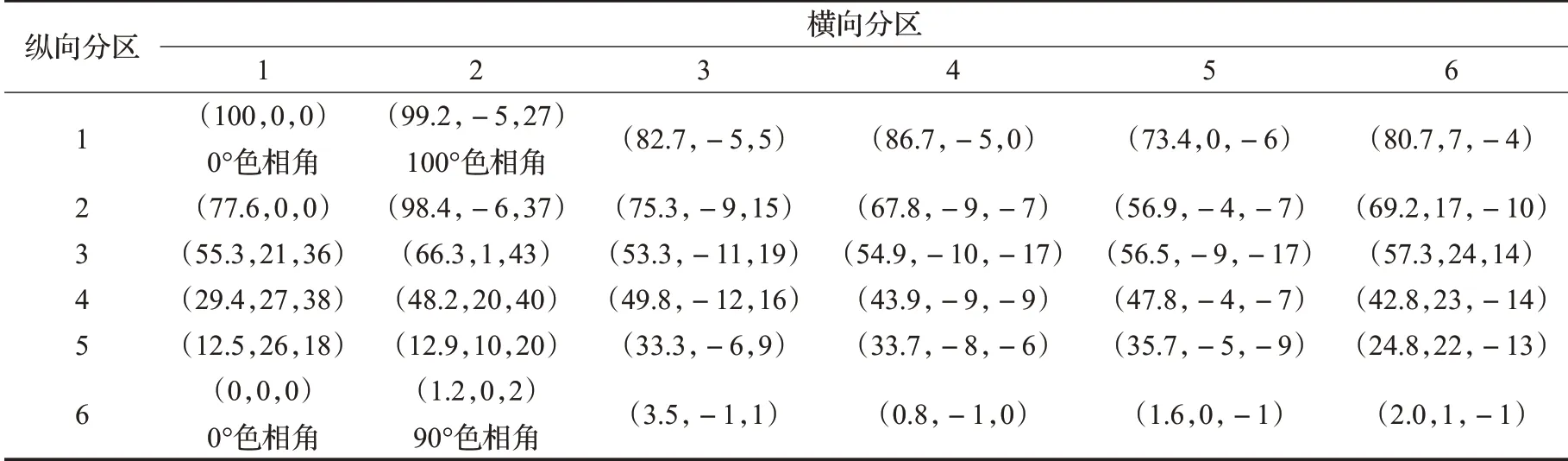
表1 原始圖像對應的色域邊界描述矩陣中各元素的CIELAB值（6×6分區）

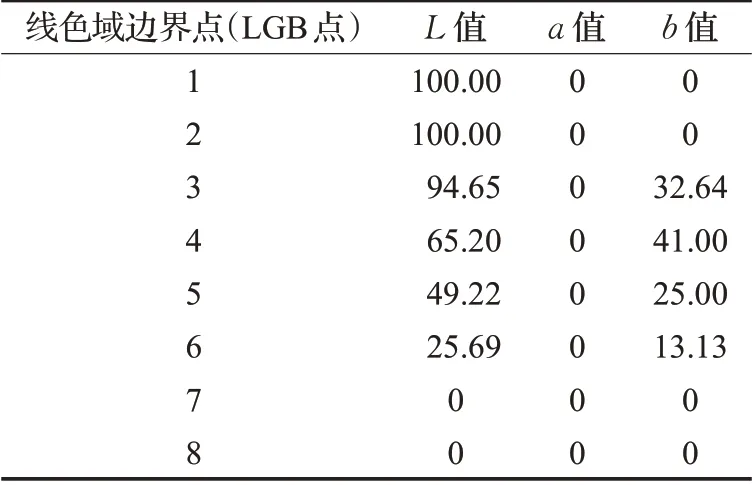
表2 像素所在等色相面內的LGB點及其CIELAB值

3 算法的性能評價

3.1 評價實驗的設計

準確地描述色域邊界，其目的是為了在不同媒體之間準確地進行色域映射。如果對圖像或設備的色域邊界描述不準確，就會直接影響到色域映射精度。因此，通過色域映射手段來評價和驗證色域邊界描述器的性能是合理而且可行的。色域映射方法按原理可以劃分為色域裁剪和色域壓縮，前者是將色域外顏色裁剪到目標色域邊界，而色域內顏色保持不變，因此它與圖像色域邊界描述并無關系，主要用于實現專色或圖表顏色的精確復制；后者是根據源色域和目標色域的關系，將色域外顏色朝映射中心的方向等比例映射到目標色域內。為了更好地保持映射圖像的階調層次，色域內顏色也可能需要映射，因此該方法主要用于彩色圖像復制。本文研究的SMGBD 空區插值算法主要針對圖像色域邊界的不規則性而提出，因此適宜選用色域壓縮的方式來評價色域邊界描述器的性能。

本文設計了基于圖像成對比較的心理物理學實驗來評價色域壓縮算法的性能，實驗在觀察條件和實驗方法等方面遵循了CIE TC 8-03 色域映射算法評價指導標準[9]。評價實驗包括準確性測試和偏好性測試。前者將每種測試算法得到的圖像分別與原始圖像兩兩顯示在顯示屏上，觀察者經過評判從中選出一幅最接近原始圖像的圖像；而后者分別將每種算法得到的圖像兩兩顯示在顯示屏上，觀察者經過評判從每對圖像中選出一幅圖像質量（顏色保真度、清晰度、彩度、局部細節等）最佳的圖像。評價用測試圖像從圖像數據庫TID2008[10]和CSIQ[11]中選取，如圖5 所示，這12 幅測試圖像涉及不同的顏色和階調特征。不同于簡單的色域裁剪，色域壓縮既要考慮目標色域范圍又要考慮源色域，因此為增強評價說服力，實驗采用的源色域和目標色域不是完全的包含和被包含關系，而是在不同的區域范圍有各自獨立的部分。源色域和目標色域分別從Samsung C27F591FD顯示器和HP z3200 噴墨打印機的ICC 特性文件中提取[12]，使用Gretag Macbeth 的Profile Editor 軟件顯示的源色域和目標色域如圖6 所示，實驗采用10×10 分區的SMGBD。實驗所用的5 種色域映射測試算法[12-15]的詳細信息如表3。

圖5 測試圖像的縮略圖

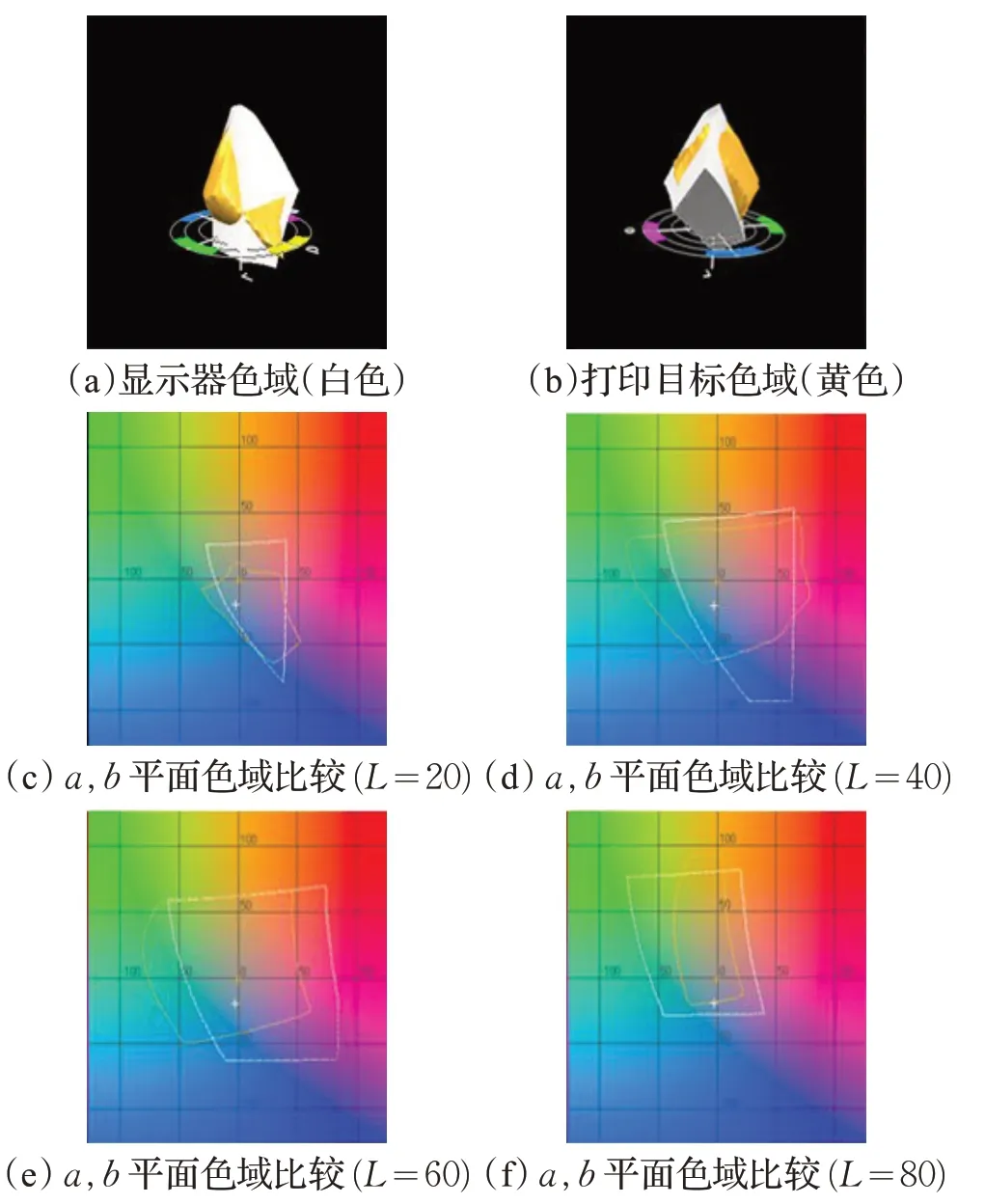
圖6 Samsung C27F591FD顯示器色域和HP z3200打印機色域范圍的比較

3.2 評價結果及分析

圖7 顯示的是根據準確性和偏好性評價實驗結果計算的每種測試算法的Z分數[15]，以及使用瑟斯頓配對定律制作的95%置信區間的等距量表。實驗觀察者由10 名圖像處理相關專業人員和10 名非專業人員組成。從圖中可以看出：偏好性Z分數與準確性Z分數的分布較為相似。在所有測試算法中，不進行色域空區插值的色域映射算法C1和S1表現較差，帶有空區插值的算法C2 和S2 表現較好，其中，算法S2 的性能甚至好于商業軟件中的對應算法S3。

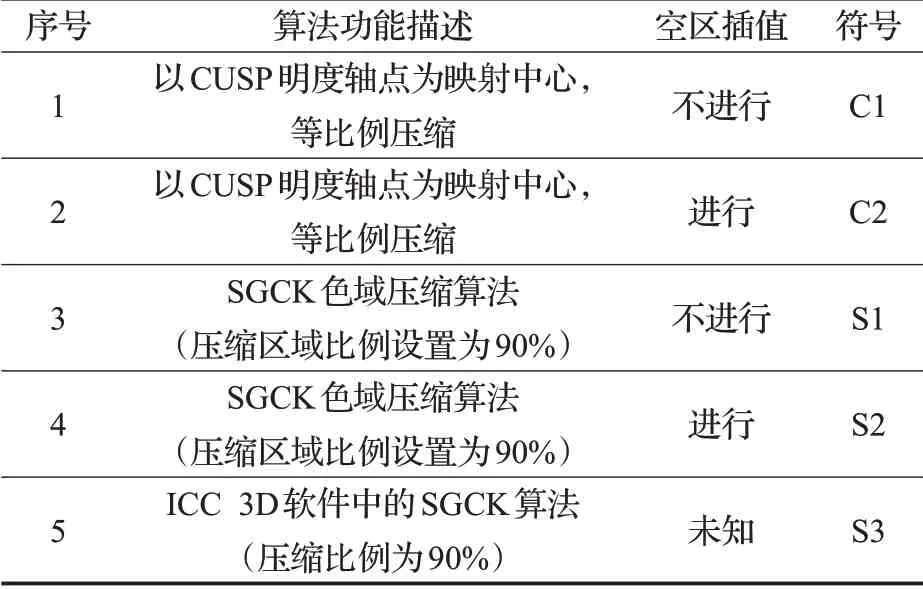
表3 評價實驗所用的5種色域映射測試算法的詳細信息

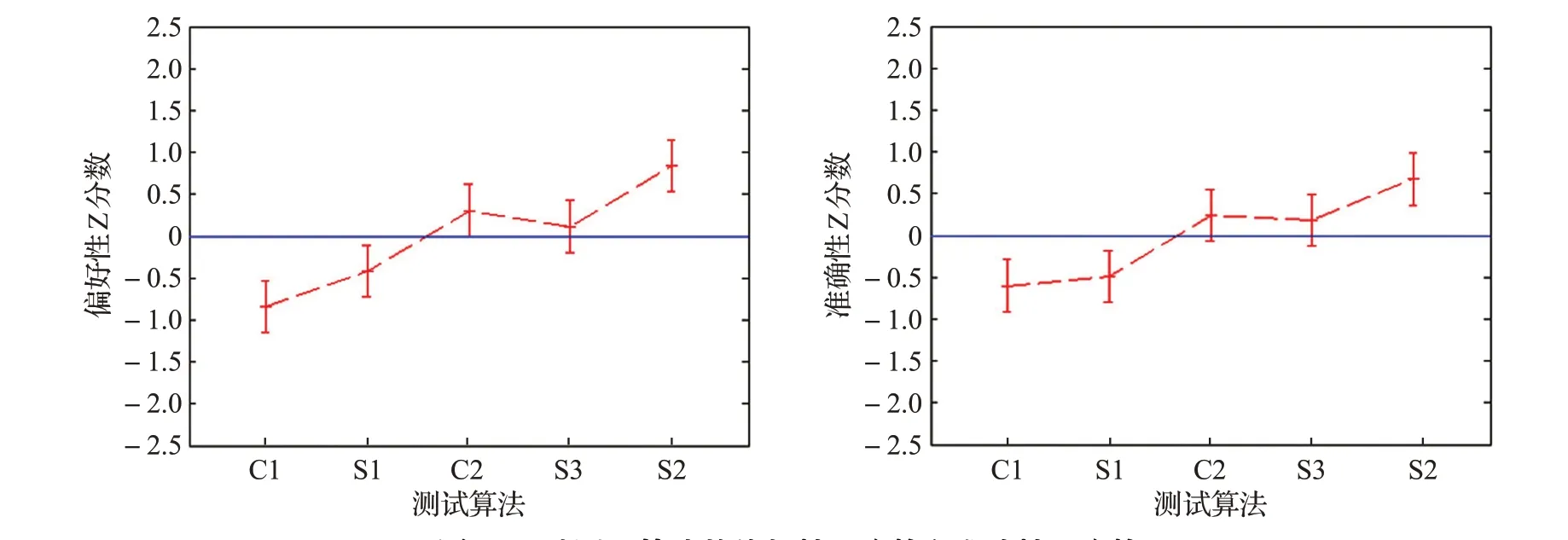
圖7 5種測試算法的偏好性Z分數和準確性Z分數

圖8顯示了無空區插值的映射算法C1對測試圖像I19 的映射效果，可以觀察到圖像中紅色方框內的區域在映射后出現了明顯的失真，如圖8（a）和（b）。通過分析發現：對于該區域內位置鄰近且顏色值非常接近的兩點Color1和Color2，其等色相面內的目標色域邊界外形非常相似，且比較規則；而圖像色域邊界相差很大，且很不規則。根據CUSP 色域壓縮原理，在圖8（c）中，在映射線OD 方向上的線段OD 大于OR（D 和R 分別是映射線與目標色域邊界和源色域邊界的交點），因此Color1無需映射。而在圖8（d）中，線段OD 卻小于OR，雖然Color2仍在目標色域內，但會按照壓縮比例映射到P 點，這就造成圖像色域內兩個顏色接近的點，因為色域邊界的描述誤差在映射后變成了兩個色差較大的像素點，從而造成了圖像失真。通過實驗發現：基于空區插值的圖像色域邊界描述更加精確，形狀更加規則，類似問題可以得到明顯改善，這也是測試算法C2 的性能明顯高于C1的原因。

圖8 映射算法C1對圖像I19的效果分析

圖9 映射算法C2對圖像I23的效果分析

通過對圖9案例的分析可以發現算法C2也存在著問題，圖9（a）中紅色方框區域的鸚鵡羽毛部位發生了明顯的映射失真，如圖9（b）。以該區域中位置鄰近且顏色值相似的兩個像素點Color1和Color2為例，在圖9（c）和（d）中，顏色點Color1位于目標色域邊界外，需要朝著映射中心O1 映射到目標色域內的P 點，導致映射后的彩度大幅度降低；Color2 位于目標色域內而不發生映射，彩度保持不變。這就造成了黃色羽毛部位在映射后出現了兩種顏色分界的失真。由于SGCK 算法并不對所有色域內顏色進行映射，而是只針對目標色域的固定比例范圍（默認比例范圍是90%）進行壓縮，因此不僅可以避免該問題，還能有效地保持部分圖像細節。從圖7還可以看出：算法S2 的性能明顯好于S3（ICC 3D 軟件中的SGCK），因為實驗中發現ICC 3D軟件中的SGCK算法對某些測試圖像會產生一些失真，如圖10，圖中的紅色區域即為映射后出現的失真區域，這也在某種程度上驗證了空區插值算法對SMGBD改進的有效性。

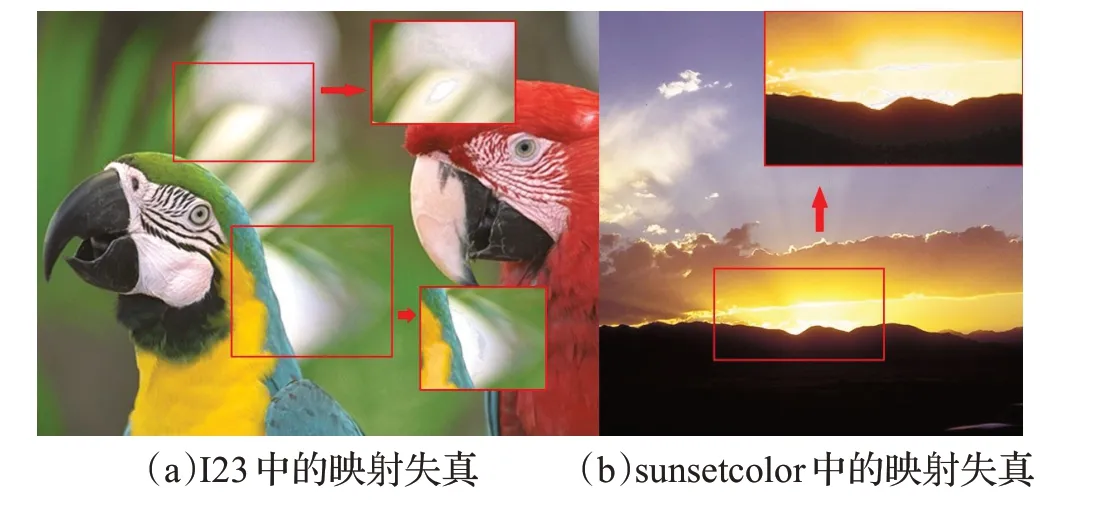
圖10 測試圖像I23和sunsetcolor的映射失真

3.3 色域邊界描述器計算效率

通過測試發現：無論是否進行空區插值，SMGBD對所有測試圖像的色域邊界計算效率都很高，且改進前后的計算時間不變（都在1 s 以內），這說明空區插值算法并不影響色域邊界的計算效率。本文還將具有相同色相角的顏色分別收集在一起進行映射，避免了同色相顏色的線色域邊界的重復計算，通過實驗發現此舉能夠大幅提升色域映射速度。本文使用色域映射算子HPMinDE[16-17]對部分測試圖像進行映射，計算時間如表4所示。可以看出：通過對圖像中相同色相角的像素進行同批映射可以大幅提高映射效率。本文算法效率的測試環境為MATLAB平臺（DELL OptiPlex，Inter?CoreTMi7-4770M CPU@3.40 GHz），源色域和目標色域的選擇與3.1節相同。

表4 不同圖像的色域映射時間 s

4 結論

本文研究了SMGBD 色域邊界描述器的空區插值和線色域邊界的計算方法，提出了基于相鄰分區加權平均的色域空區插值算法，從而可以更加準確地計算出各分區的色域邊界點。針對相鄰分區邊界點連線與等色相面重合所導致的色域邊界計算和色域映射問題，本文給出了合理的解決方案，并通過案例分析驗證了方案的可行性；在評價部分，本文借助色域映射的方式，利用心理物理學實驗評價了空區插值算法的效果，同時還測試了算法的計算效率。評價結果顯示：本文提出的色域空區插值算法能夠有效提升色域邊界描述器的精度，改善色域映射效果，而且并不影響色域邊界的計算效率。