基于賦時Petri網的景區游客分流研究

陸文星，王琥珀，王彬有

合肥工業大學 管理學院，合肥230009

1 引言

隨著我國旅游行業越來越龐大[1]，在旅游旺季和節假日游客大規模的集中出行，使得景區經常出現游客擁擠現象，不僅對景區的生態環境保護嚴重破壞，甚至引發踩踏等一系列的安全問題，造成嚴重的人員傷亡和經濟損失[2-5]。因此，旅游高峰期景區的游客管理工作越來越受到重視和關注。景區的自然環境容量代表了景區在保證自身生態環境不受到破壞的情況下，能承載的最大人數，而對于游客來說，景區的游客量超出一定界限后，游客的滿意程度會隨著人數的增多而越來越低[6]。所以在旅游高峰期時，在保證景區內景點不超載的情況下，使得游客在景區內分布更加均勻平衡是景區管理工作的重中之重。

許多學者從各個方面對景區分流問題進行了研究，但大多都是針對某一具體的景區的實例研究，沒有普適性的理論成果給不同景區的分流工作進行指導。如肖雄輝、戈鵬等以九寨溝風景區為例，通過引力分流調度模型來控制游客在景區內的分布，但模型假設中將景區的臨界值設為無窮大，即使在游客數量超載的情況下仍不會拒絕游客進入，與實際情況不符合[7]；李坤毅、陳炫宇等將無線射頻技術引入分流導航設計模型，掌握每一個游客的實時信息和位置來進行游客的疏導，但沒有提出具體的分流的方法[8]；潘航以北京故宮景區為例，分析了游客在高峰期時時空分布特征，并提出了分流對策，但不能夠根據游客的實時信息做出動態的調整[9]；胡明明、趙容等對景區內景點間不同交通方式的分流比率進行仿真模擬，并以管理熵作為評價標準，但忽略了景點自身的屬性[10]。

Petri網作為一種圖形化的建模工具，它具有精確的定義，有堅實的數學基礎支撐，被廣泛地應用于計算機和自動化技術領域。在實際應用中，根據現實情況對其顏色、時間和層次等進行擴展，形成了高級Petri 網[11]。如Zuberek 在普通Petri 網的基礎上加入了時間因素構成了時間Petri網，并給出了其基本定義及構造方法，解決了系統建模無法與時間關聯的問題[12]；Molloy等人把變遷與隨機的指數分布實施延時聯系起來，得到了隨機Petri網，利用它建模可以分析有隨機過程的系統中部件的利用率、系統的吞吐量和延時等指標，但是在利用隨機Petri網進行模型分析時系統的狀態空間會隨著系統規模的增大而指數性地增長，使得與其同構的馬爾可夫鏈難以求解[13]；楊健維、何正友將Petri 網引入電網警報處理和故障診斷，有效地處理警報信息中的各種情況，并使診斷結果更加精確[14]；李景峰、張艷等選用分層Petri網建立面向對象的分層Petri網模型，實現對供應鏈中物流、信息流和資金流的優化分析，但在約束條件的設置上不夠精確，有待優化[15]；王列偉、吳朔等提出一種自上而下的離散和連續Petri網的混合模型，通過對不同系統負載下交叉口內交通流排隊長度的仿真考察模型的誤差，來證明模型的優越性，但在排隊長度上有限制，與實際情況不太符合[16]；賈麗臻、檀潤華等將時間元素注入Petri 網，模擬系統中的能量流、物料流和信息流元素和有色Petri網結合對系統行為進行優化，但在優化產品時序過程方面不夠客觀[17]。李海燕、王艷萍等針對柔性制造中出現死鎖的問題，提出基于分支定界法的Petri網，分別設計了集中式監控器和分布式監控器，但在特殊情況下，加入控制子網后，會產生新的死鎖，并沒有完全解決問題[18]。

Petri 網因為其直觀的模型表達和狀態轉移持續性的特點，同樣適用于景區游客的動態游覽問題，本文在考慮到游客在景區內的動態游覽特點下，針對旅游高峰期景區穩態分流中部分熱門景點客流量過多以及景區游客分布不均衡的實際問題，以游客在景區內時間和空間分布上的情況為基礎，本文提出賦時Petri 網（Petri Net With Time，PNWT）的景區游客分流的8 元組動態模型Σ=(P,T,F,ω,M,σ,f,m0)。提出基于權重、平均分流、基于景點綜合負載率以及基于路線下游景點綜合負載率四種分流策略，以基于景點自身屬性的評價標準游客滿意度和負載率為評價標準來與傳統分流策略作比較。并采用仿真實驗分析在不同分流策略下景區負載率方差和游客滿意度兩種評價標準的變化趨勢，并在不同評價標準下選用合適的策略來解決景區游客穩態分流問題，本文所提出的模型方法具有普適性，對后期景區游客時空分流的研究以及景區管理工作有重要的參考價值。

2 賦時Petri網建模

在景區客流量高峰期時，景區管理部門需要針對部分景點存在的超載問題進行游客分流的工作，為了更好地描述景區景點之間的相互關聯關系，本文提出PNWT的景區游客動態游覽模型，本章介紹賦時Petri網模型的構建，包括賦時Petri網的定義、數學模型的相關概念。

2.1 模型定義

一個賦時Petri網模型定義如下：

Σ=(P,T,F,ω,M,σ,f,m0)為描述景區動態分流過程的賦時Petri網，其中：

P={p1,p2,…,pn} 為有限景點的集合，n 為景點的個數。

T={t1,t2,…,tn-1}為有限客流量流動的集合。

F=(P×T)?(T×P) 為有限的景點間連接道路集合，則T →P 為映射變遷到其所有輸入庫所的輸入，即流入景點的客流量，P →T 為映射變遷到其所有輸出庫所的輸出，即景點分流的客流量，則(P,T,F)為有向網，稱為Σ 的基網。

ω={ω1,ω2,…,ωn}是景區所有景點權重的集合，代表了景點的著名程度和游客的選擇傾向，且

m0表示每個景點的初始狀態，即初始游客數量。

M 表示每個景點游客的最大容量。

σ={σ1,σ2,…,σn}為游客在景點的平均停留游玩時間。

f=(fij)n×n為第i 個景點到第j 個景點的時間距離，即用兩個景點之間移動所需要時間的大小來表示景點間距離的遠近，且fij=fji，i,j=1,2,…,n。

如圖1 所示，圖中P1、P2分別表示兩個不同的景點，景點間通過客流量的流動T1連通，每個景點都有自身的屬性：M,m,ω,σ 分別代表該景點的最大游客容量，當前景點的游客數，該景點的權重，游客在該景點的平均游玩時間。每一個客流量的流動T 都有一個表示兩邊景點時間距離的屬性f 。從景區的入口開始，將所有景點按照這種規則連通起來，就形成了整個景區的Petri網模型。

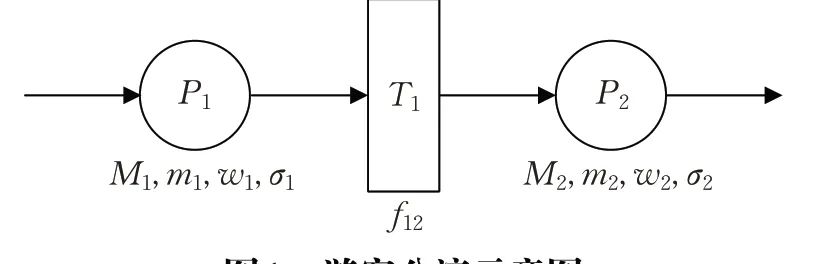
圖1 游客分流示意圖

2.2 數學模型

在j 時刻，景區景點游客的負載率計算公式如下：

其中，mij表示第i 個景點在j 時刻的游客人數，Mi表示第i 個景點的最大游客容量，lij表示第i 個景點在第j 時刻的景點負載率。

景點的空載率eij公式如下：

其中，eij表示第i 個景點在第j 時刻的空載率。平均負載率公式如下：

ωi表示第i 個景點當前的權重，Lave代表整個景區在第j 時刻的所有景點的平均負載率。

負載率方差公式如下：

Eij表示在第j 時刻第i 個景點的負載率方差，Eij越小，代表該景點此時的負載率與平均負載率越接近，E 代表了景區只考慮景點負載率的評價方式。

在j 時刻單個景點游客滿意度公式如下：

其中，sij代表第i 個景點第j 時刻的游客滿意度，eij代表j 時刻該景點的空載率，α 為大于0的正數，代表游客滿意度與空載率eij的正相關性，mij代表j 時刻該景點的人數，ωi代表該景點的權重。 s 代表了考慮到景點自身屬性的評價標準。

景區管理運營的目標就是提高游客的滿意度以及降低景區內負載率方差，因此模型的目標函數分別為：

3 游客分流策略

3.1 游客分流假設

景區內部游客的分布研究是一個復雜的系統研究，涉及到游客在景區游玩的時間分布問題，景區內載客工具的調度，游客選擇不同交通線路，以及不規律的游客休息問題。本文主要研究景區內不同分流策略對游客滿意度以及景區景點負載率的影響，因此作出如下假設：

（1）本文研究的是景區高峰期游客的分布情況，因此在實驗中假設這段時間內大量游客都是瞬時進入景區。

（2）在實際情況中景區內景點與景點之間可能存在不同交通工具，選擇不同方式去往下一個景點的時間也不相同，本文中假設兩個景點之間的移動方式只有一種，即兩個景點之間的時間距離是唯一的。

（3）游客在一次完整的游玩經歷中，在從景區入口進入景區到從景區出口離開景區的過程中，盡可能不會重復游覽已經游過的景點，且在某個景點達到該景點設定的平均游玩時間時會去往下一個景點，形成游客的自然流動。

3.2 游客分流流程

游客在景區的分流流程如圖2所示，其中關于基于時間約束Petri 網的游客分流的處理流程的相關定義如下：

（1）Q={q1,q2,…}為超載的景點集合。

（2）PNWT為根據游客分流中運行規則得到的Petri網模型。

（3）A={a1,a2,…}是景區接收到即將進入景區游客數量信息的集合。

（4）R={r1,r2,…}為時間約束規則中進行分流的景點的集合。

（5）L={l1,l2,…}為超載景點與其可分流的目標景點的集合，表示為{l1,l2,…}={(q1p1,q1p2,…),(q2p1,q2p2,…),…}，其中Q 集合中的景點僅與其相鄰的景點取值有意義，其余均為空值。

（6）I={i1,i2,…}為滿足規則的分流信息集合。

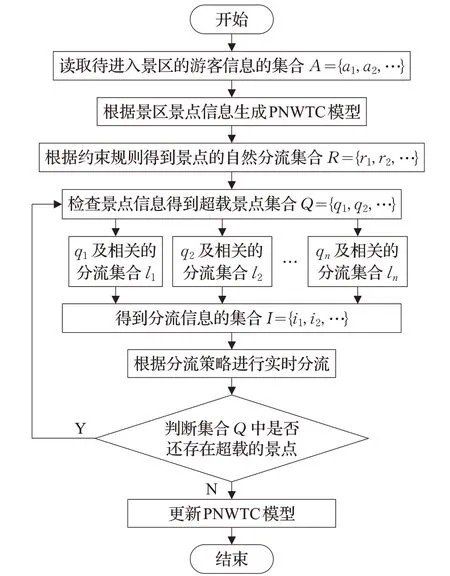
圖2 景區游客實時分流流程圖

3.3 分流策略

景區游客客流量的分流管理一般從初態分流、穩態分流和終態分流三個階段[19]進行研究，初態分流和終態分流分別是指游客進入景區內部之前和離開景區之后，景區的工作人員通過對車輛等交通設施的疏散和管理，使得景區入口、景區初始狀態和出口處游客均勻分布，這兩個階段的游客分流不是本文研究的重點，不做過多的贅述。在穩態分流中，當景區內某景點的游客在游玩完該景點之后將會去往下一個景點，這屬于景區的自然分流；或者當某景點的游客量超過了該景點的承載上限，需要景區管理人員根據景區其他景點的狀況來進行人工分流，這屬于景區的強制分流，這兩種情況都會面臨相同的問題，即被分流的游客應該分流至哪一個景點，以及分流至下游景點的比例。游客的時空分流是解決景區內游客擁擠，保護景區生態環境的重要手段，基于景點負載率的分流策略，即通過下游景點的負載率來確定目標分流景點以及分流的比例，是解決上述問題的重要方法[20]，本文提出平均分流、基于下游景點權重、基于下游景點綜合負載率和基于下游路線綜合負載率4種分流策略同傳統的基于景點的負載率分流策略相比較，探尋在不同分流策略下每個下游景點所獲得分流游客的比例，以及不同策略下景區負載率方差和游客滿意度的變化趨勢。假設存在需要分流的客流量M*時4種分流策略的具體思想如下：

（1）分流策略1。平均分流，即在景點人數超出景點容量時，將超出的人數平均分流至相鄰的其他景點。如圖3，當景點P1的客流量m1超過景點的游客最大容量M1時，采取平均分流的方法將需要分流的游客平均分流至下游節點，即景點P2和景點P3都獲得M*/2 的客流量。

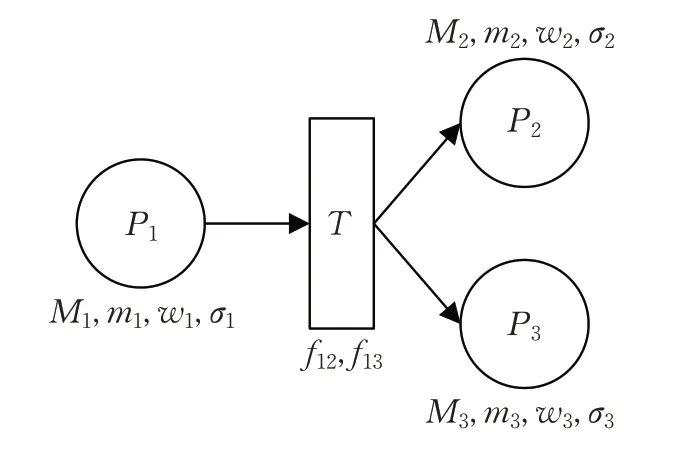
圖3 策略1、2、3示意圖

（2）分流策略2。基于下游景點權重實時分流，即比較相鄰景點的權重，按照權重的大小決定分流的景點以及比例。如圖3，當景點P1存在需要分流的游客時，采取基于下游景點的權重來決定分流的比例。即景點P2、P3獲得的客流量為ω2M*/(ω2+ω3)、ω3M*/(ω2+ω3)。ω2、ω3分別代表景點P2和P3的權重。可以從公式看出，景點的權重越大，獲得分流的游客數量就越多，對應到實際情況就是景點的知名度和吸引力越大，獲得的分流游客就越多。

（3）分流策略3。基于下游景點綜合負荷度實時分流，即比較相鄰景點的綜合負荷率，來決定景點獲得分流游客的比例。如圖3所示，景點的負荷率不僅和在景點的游客人數相關，還和上游景點與下游景點之間的時間距離以及下游景點的平均逗留都有關系，時間距離和游玩時間越長，說明在相同的時間內該景點接待的游客數量就越少，說明該景點不適合獲得過多的游客分流，與負載率正相關。而景點的權重會影響到游客的選擇傾向和滿意度，景點的權重越大，對于游客來說就越有吸引力，游客游玩該景點的意愿就越強，會降低負載率的影響，與負載率負相關。具體的計算公式如下：

kij代表了第i 個景點在j 時刻的綜合負荷率，σi代表該景點的游客平均游玩時間，f 表示上下游景點之間的時間距離。根據景點的綜合負載率可得景點P2和景點P3的獲得分流的客流量分別為k3M*/(k2+k3)和k2M*/(k2+k3)，從公式可以看出，綜合負載率越小的景點，獲得分流游客的數量越多。

（4）分流策略4。基于下游路線綜合負荷度實事分流，即比較不同路線的綜合負荷率，選擇綜合負荷率較小的路線。景區內的景點的負載率不是獨立存在的，往往受到同一條線路上的其他景點影響，正是考慮到這種影響，在游客分流的時候不僅考慮當前景點的綜合負載率，同時要考慮不同線路上的后續景點帶來的影響。若后續景點的負載率較小，則這條線路上應該獲得較多的分流客流量，若后續景點的負載率較大，則應該適當減少這條路線上所獲得的客流量，同時這種影響也和景點距離路線節點的距離有關，距離越遠的景點，影響力就會越小，因此具體的計算公式如下：

其中，rij表示在j 時刻第i 個景點基于路線的綜合負載率，f 表示路線上初始景點與路線節點之間的時間距離，hi表示路線上每個景點到路線節點的時間距離，hi包括景點與景點之間的時間距離和景點自身的平均游玩時間，且隨著hi的增大，該景點產生的影響減小。將路線上的景點負載率以時間距離加權平均即得到該景點基于路線的綜合負載率。如圖4所示。

例如圖4中G1,G2分別代表景區的入口和出口，景點P1和景點P3是路線節點。該景區的游覽路線分別是：（1）1-2-4-7；（2）1-3-5；（3）1-3-6-8。當景點P1處于超載的狀態時，根據路線可知，景點P2的后續景點有P4、P7，景點P3的后續景點有P5、P6、P8，分別計算出景點P2、P3基于路線的負載率r2、r3，計算公式如下：

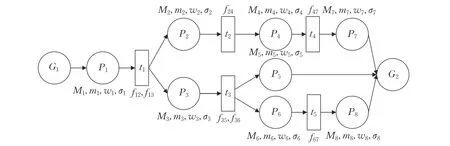
圖4 策略4示意圖

則可得景點P2和景點P3的獲得分流的客流量分別為

4 仿真實驗與結果分析

在自然狀態下，景區內游客隨機的游覽景點會導致景區內景點的負載率不斷發生變化，尤其在旅游高峰期，景區內的一個或幾個景點會出現游客的數量達到甚至超過當前景點游客數量的容納上限。此時如果景區的管理人員不對超載景點進行人工的游客分流管理，將會導致超載景點的游客數量持續增加，最終導致景區內各個景點的游客負載率急劇不平衡，影響游客的滿意度。為了更好地驗證基于時間約束Petri網模型的適用性和分流策略的有效性，本文借助仿真實驗進行比較分析，采用虛擬時鐘通過時間的變化（時鐘每增加一個步長，檢驗每一個時間約束是否觸發，檢驗完成后，更新到下一個時刻）來模擬游客流動和景點游玩的過程。

景區常見的景點分布情況有三種：單向性、多向性和復雜性[20]。而綜合文獻[7]、[9]、[10]、[20]來看，景區的客流量高峰期大部分處于8點到11點，持續時間最少為3 h，少部分景區7點到8點，11點到12點同樣處于高峰期，持續時間更長，景區的景點在高峰期的時間段內出現部分景點處于超載的情況。考慮到以上情況，本文仿真實驗中的虛擬時鐘時長確定為240 min，步長為1 min，景點空間布局如圖5所示。

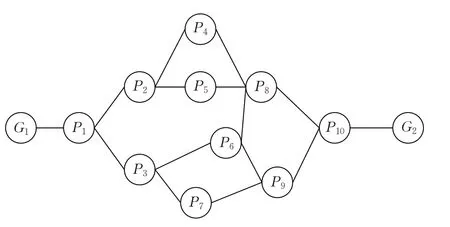
圖5 仿真實驗景區景點空間分布圖

圖5 中，G1代表景區入口，G2代表景區出口。P1,P2,…,P10代表景區內的景點。景點之間的連線代表兩個景點之間相通。為了更好地說明動態分流算法的應用過程和簡化仿真實驗，本文的仿真實驗做出以下說明：

（1）因本實驗模擬高峰期游客分流問題，所以游客進入景區時都是瞬時發生，以虛擬時間鐘的步長為單位時間，每個單位時間開始時，都會有固定數量的游客g0進入景區，在景區內的游客從入口G1處進入景區，游客只能按照景點分布圖中的道路移動，最終從出口G2離開景區。

（2）模型的時間信息代表了游客在景區的游玩逗留時間，游客每個景點的逗留時間不完全一樣，且不同景點的時間約束觸發條件獨立，當實驗中虛擬時鐘的時間點滿足是某景點時間信息的整數倍，則觸發該景點游客分流，在時間信息條件被滿足之后，觸發的景點都有20%的游客需要離開當前景點，且只能向相連的景點分流。經過不同景點之間的時間距離后到達目標景點。仿真實驗預先輸入的參數包括：①每個景點的游客平均游玩時間和最大客流量容量；②每個景點的權重以及上下游景點之間的時間距離；③實驗期間游客進入景區的速度（人/min）；④景區的初始狀態；⑤數學參數。具體如表1 和圖6所示。

表1 景點參數表

圖6 景點時間距離示意圖

表1 中的數據分別代表了景區中每個景點的最大容量M ，每個景點的游玩時間σ ，每個景點的權重ω，f 表示相鄰景點之間的時間距離，不存在直接連通的景點之間的時間距離取0。景區的初始狀態由實驗隨機給出，不同的景區初始狀態會對景點的初始時刻的負載率有影響，但不會影響負載率相關數據的整體發展趨勢，取游客進入景區的速度為g0=50 人/min，為便于計算，?取1。

實驗輸出的參數包括：（1）每個時刻景區的平均負載率；（2）每個時刻景區的負載率方差；（3）每個時刻所有景點游客的滿意度之和。

本實驗采用MATLAB R2014a 軟件進行仿真，在4種策略以及經典策略下，景區的負載率方差和游客滿意度實驗結果如圖7～圖11所示。

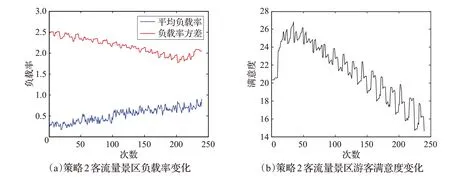
圖7 經典策略下時刻圖

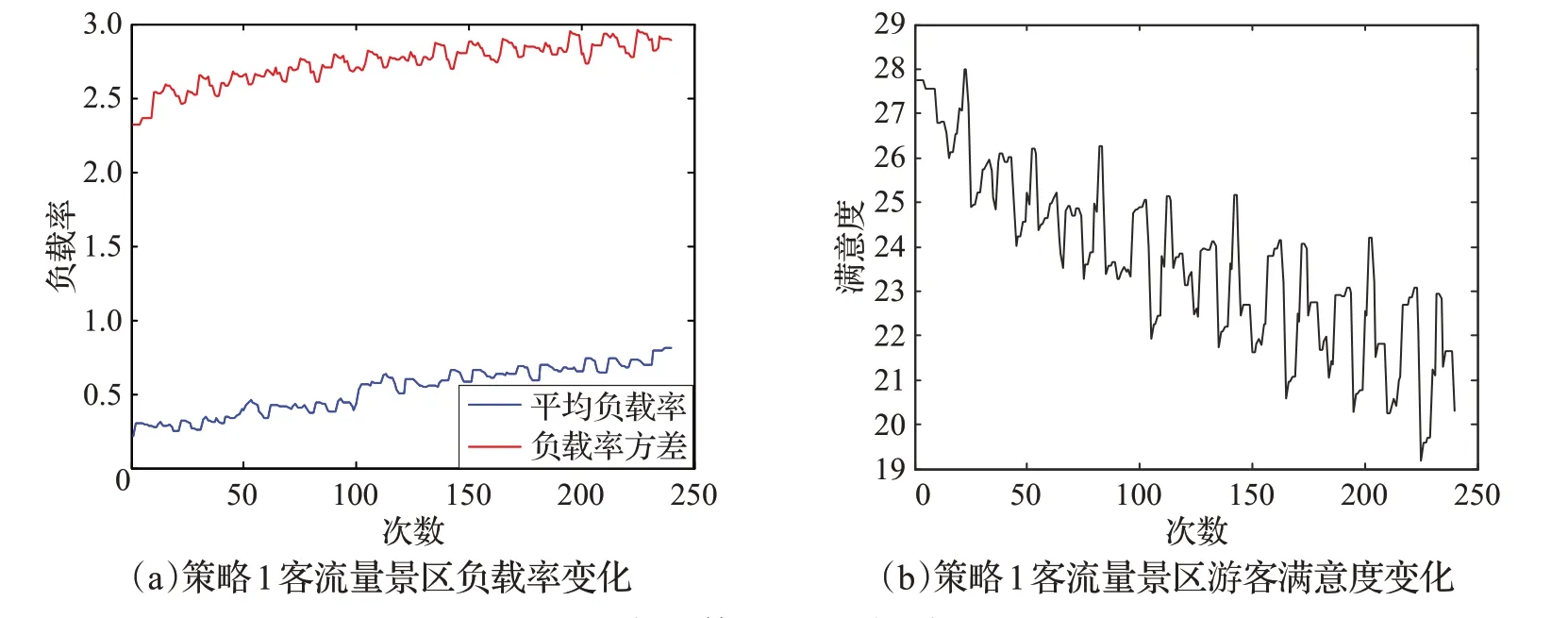
圖8 策略1下時刻圖

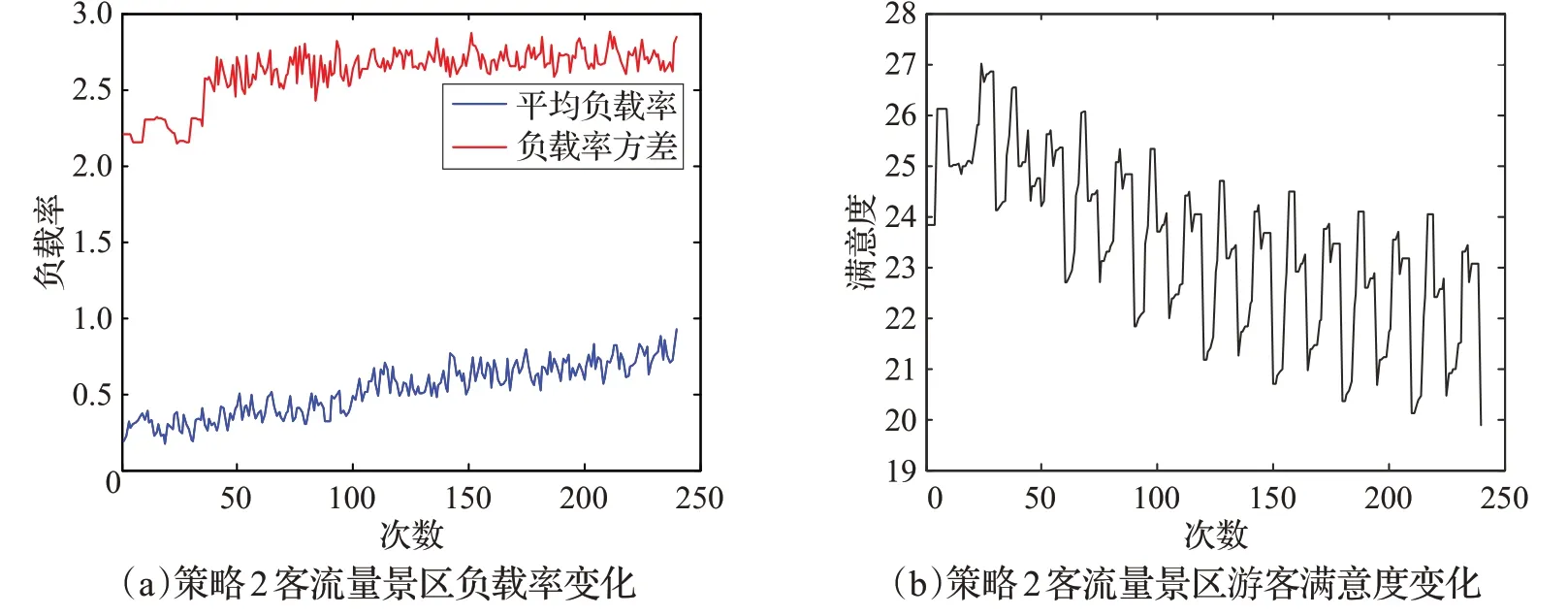
圖9 策略2下時刻圖

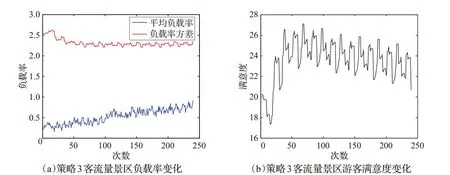
圖10 策略3下時刻圖

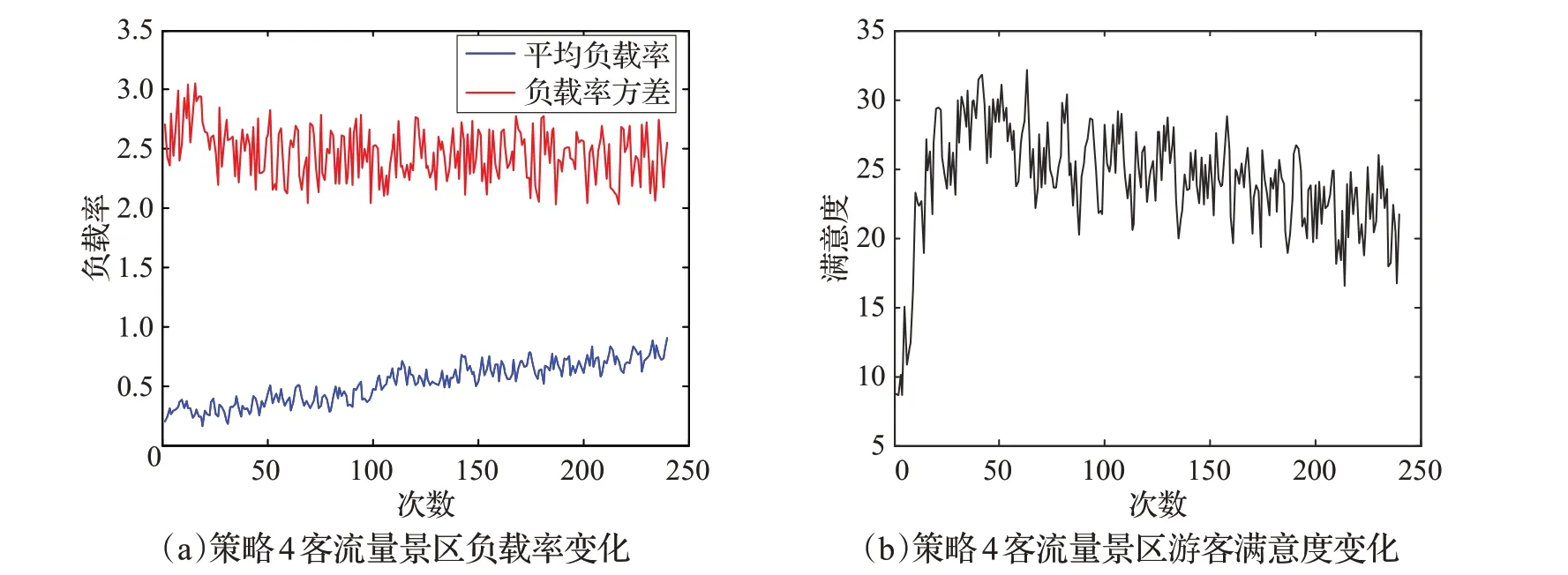
圖11 策略4下時刻圖

圖7 為經典策略基于景點負載率策略下景區每分鐘平均負載率、負載率方差和游客滿意度的時刻圖。從圖中可以看出隨著景區游客增多，平均負載率增大，景區的負載率方差呈現出下降的趨勢，說明采用基于景點負載率的分流策略可以有效地降低景區負載率方差，使景區內游客分布得更加均勻；景區的游客滿意度呈現出先上升后下降的趨勢，原因是隨著景區內游客的變多，每個景點的滿意度逐漸上升，又因為景點人數的增多，空載率下降，滿意度隨之減少，且隨著游客的越來越多，空載率趨向于0，曲線下降的幅度增大，所以出現先上升后下降的形狀。

圖8為平均分流策略下景區每分鐘平均負載率、負載率方差和游客滿意度的時刻圖。隨著景區進入游客的數量增多，景區的平均負載率和負載率方差逐漸上升，而游客的滿意度逐漸下降，且下降幅度較大，說明該策略不能很好地解決景區內景點游客分布不均勻的問題，原因為沒有考慮下游景點的情況。

圖9 為基于景點權重策略下景區每分鐘平均負載率、負載率方差和游客滿意度的時刻圖。可以看出該策略下隨著平均負載率的增加，負載率方差急劇上升，且一直保持較大的數值，說明該策略對于降低景區負載率方差并沒有作用；從游客滿意度曲線上來看，游客滿意度呈現出先上升后持續下降的趨勢，且下降的幅度較大，說明該策略對于提升游客滿意度的作用較小。

圖10為基于景點綜合負載率策略下景區每分鐘平均負載率、負載率方差和游客滿意度的時刻圖。從圖中可以看出該策略可以有效地降低景區的負載率方差，使得游客在不同景點的分布更加均勻，且趨向于穩定。從游客的滿意度曲線的形狀來看，在初始時刻，滿意度下降，可能是由于景區初始狀態的影響，但之后曲線的整體情況呈上升趨勢，而后在曲折中緩慢下降，說明該策略不僅能夠解決景區負載率不均衡的問題，同時對于在高峰期提高游客的滿意度同樣有作用。

圖11為基于下游路線景點綜合負載率策略下景區每分鐘平均負載率、負載率方差和游客滿意度的時刻圖。從圖中可以看出隨著景區游客的增多，平均負載率的增大，景區的負載率方差呈現出小小的下降趨勢，但曲線反復地變化，說明該策略對于降低景區內負載率方差的效果并不明顯，原因在于該策略中分流游客到目標景點以及后續的下游景點需要的時間比較長，所以曲線的波動比較大。而游客的滿意度曲線同樣呈現先上升后下降的趨勢，且下降的幅度較小，說明該策略對于提升游客滿意度有著較明顯的作用。

綜合以上4 種策略以及傳統策略來看：（1）在負載率方差方面，策略1 和策略2 下景區的負載率方差呈上升趨勢，說明該策略在降低景區負載率方差方面沒有發揮作用；傳統策略和策略3下的景區負載率方差都呈現下降趨勢，且比較穩定，說明這兩種策略對于降低景區負載率方差有較明顯的作用，而傳統策略下景區的負載率方差最大為2.514，最小為1.784，策略3下景區的負載率方差最大為2.615，最小為2.202，說明傳統策略的效果更好，策略3的穩定性更好；策略4下的景區負載方差呈現出一定的下降趨勢，但曲線上下波動幅度較大，不夠穩定，對于降低景區負載率方差的作用不太明顯。（2）在游客滿意度方面，策略1 和策略2 下景區游客的滿意度一直呈現下降的趨勢，說明該策略對于提高游客滿意度沒有作用；傳統策略下景區游客的滿意度呈現先上升后下降的趨勢，但下降幅度太大，說明該策略對提高游客滿意度的作用較小；策略3 和策略4 下景區游客的滿意度曲線形狀較為相似，呈現出先上升后下降的趨勢，且下降的趨勢較緩，說明這兩種策略對于提高景區游客滿意度都有較明顯的作用，而策略3下景區游客滿意度曲線大部分處于[20.7，27.11]，平均值為23.91，策略4下景區游客滿意度大部分處于[18.23，32.16]，平均值為25.12，說明對于游客滿意度策略4的效果更好，而策略3更穩定。（3）綜合景區負載率方差和游客滿意度來看，如果將景區負載率方差作為評價標準，采用傳統策略的效果更好；若將游客滿意度作為評價標準，采用策略4 的效果更好；若同時將兩者作為評價標準，策略3更好。

5 結論與展望

在旅游高峰期，大量游客涌入景區造成景區熱門景點超載以及景區負載不均衡的問題，對于景區的生態環境和游客自身的生命安全都造成了損害，本文針對以上問題，將景點、游客對應于Petri網系統中的元素，并注入了時間元素，具體工作如下：

（1）為了更好地描述景區內景點之間游客動態分流實際過程，根據游客動態游覽的特點、景點的自然環境容量問題以及其存在的時間距離關系，本文提出賦時Petri網的8元組模型Σ=(P,T,F,ω,M,σ,f,m0)，并對數學模型相關概念進行解釋。

（2）提出基于權重、平均分流、基于景點綜合負載率以及基于路線下游景點綜合負載率四種分流策略來與傳統分流策略作比較。

（3）提出基于景點自身屬性的評價標準游客滿意度，并采用仿真實驗分析在不同分流策略下景區負載率方差和游客滿意度兩種評價標準的變化趨勢，并在不同評價標準下選用合適的策略。

本文所提出的分流策略，具有普適性，對于大部分景區的穩態分流管理的實際工作都有重要的參考價值。此外，為進一步探索景區游客的時空分布特點以及更有效率分流策略，后續研究將重點放在以下兩個部分：

（1）考慮到實際情況中景點之間存在多種交通線路，即兩個景點之間的時間距離不唯一，進一步研究在這種情況下整個景區游客的時空分布特征以及分流策略的選擇情況。

（2）對于景區景點生態環境的屬性做進一步的思考，提出更全面有效的評價標準，在實驗中景區的參數設置更合理，更貼近實際。