基于QoS的D2D能效優化

李少華，覃錫忠+，賈振紅，馮 剛，曹傳玲

(1.新疆大學 信息科學與工程學院，新疆 烏魯木齊 830046；2.中國移動通信集團新疆有限公司 計劃部，新疆 烏魯木齊 830046)

0 引 言

隨著智能終端的指數型增長，巨大的能源消耗成為了5G的關注點[1]。D2D通信作為解決5G通信中頻譜資源利用率和系統能效的關鍵技術備受關注[2-4]。D2D用戶復用蜂窩用戶設備(cellular user equipment，CUE)的頻譜資源對CUE通信造成的干擾[5]，使得CUE通信服務質量變差。因此如何有效降低CUE和D2D用戶之間的干擾，提高系統能效是重要的研究課題之一。文獻[6]研究的是能效和延遲之間權衡。文獻[7]提出一種基于非線性分數規劃的迭代功率分配算法來解決能效優化問題。文獻[8-11]主要解決在保證用戶傳輸速率的條件下，能源效率最大化問題。文獻[12]提出一種高效的迭代資源分配的方案提高系統能效。上述文獻均未將干擾問題作為主要的待解決問題。

針對D2D用戶與CUE之間的干擾問題，李旺等提出了一種資源分配算法[13]，在保證用戶QoS的條件下最大化系統傳輸速率。本文在此基礎上進行改進，提出新的優化模型：在考慮用戶QoS的條件下，最大化系統能效，同時保證傳輸速率。針對優化問題中遇到的NP難題，提出一種啟發式資源分配算法，并將其分為兩部分：一是利用松弛方法忽略次要干擾的影響，降低算法的復雜度；二是縮短復用資源的搜索范圍，降低D2D用戶與CUE的匹配時間。仿真結果顯示，利用本文算法1-search可以降低搜索時間，提高系統能效，同時加快收斂速度。

1 系統模型和問題描述

1.1 系統模型

在D2D復用頻譜資源過程中，對CUE產生的干擾，一部分可以通過基站(base station，BS)進行控制，另一部分利用資源分配的算法進行復用資源的分配。因此在研究D2D用戶復用資源時，大多數研究者考慮的是上行鏈路(uplink，UL)[14-16]。本文的系統模型采用的是最基本的上行蜂窩網絡結構，如圖1所示，其中包含N個CUE和M個D2D對用戶(M≤N)，分別用C={1,2,…,N}，D={1,2,…,M} 表示，N個CUE被預先分配N個正交信道，且沒有多余的信道供D2D用戶使用。在頻譜復用過程中，D2D用戶和CUE都有最小QoS要求，用中斷概率來表示，因此控制一個D2D對只能復用一個CUE的信道資源。

圖1 系統模型

信道模型如圖1所示，第i個CUE到基站之間的信道增益和第j對D2D之間的信道增益分別用gi,B和gi表示；第j對D2D發射端到基站的干擾信道增益和第i個CUE到第j對D2D接收端的干擾信道增益分別用hj,B和hi,j表示。在D2D通信系統中，BS負責各系統的資源分配任務，因此需要獲得整個系統所有用戶的信道狀態信息(channel state information，CSI)。CSI的獲取有兩種方式：一種是完全信道估計即瞬時信道參數，瞬時參數是已知的，且在慢衰落信道中CSI基本不變。但實際情況中由于BS獲得的CSI都是從各個用戶節點反饋回來的，在這個過程中，瞬時狀態信息的獲取需要占用大量的信令開銷，因此為節約成本，一般不使用瞬時參數。另一種是不完全信道估計即統計信道參數，統計參數是經過多次訓練統計出來的比較準確的CSI，它不需要像瞬時參數那樣時時刻刻進行CSI的統計，也能獲得較準確的數據。在快衰落信道中多采用的是統計信道參數[17-20]。

統計信道參數采用文獻[13]中的瑞利信道參數模型，信道增益服從指數分布。若隨機變量X服從參數為λ的指數分布，則概率密度函數表達式為

(1)

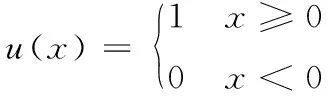
D2D鏈路中：gj～exp(γj)，hi,j～exp(γi,j)，γj和γi,j分別代表D2D鏈路的信道功率增益的期望和干擾鏈路的信道功率增益的期望。

UL鏈路：gi,B～exp(αi)，hj,B～exp(αj)，αi和αj分別代表UL功率增益的期望和干擾鏈路功率增益的期望。

1.2 中斷概率

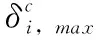
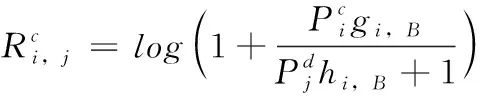
(2)

蜂窩鏈路和D2D鏈路的中斷概率限制表示為

(3)

1.3 優化模型

基于QoS要求的系統能效EE優化模型如下

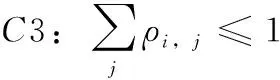
C5:ρi,j∈{0,1} ?i∈C,j∈D

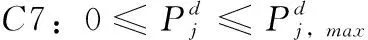
(4)

式(4)中，當ρi,j=1時，表示第j對D2D用戶找到了符合用戶QoS要求的第i個CUE共享頻譜資源。在限制條件中，C1和C2表示對用戶中斷概率的要求，即CUE和D2D之間的相互干擾要限制在一定范圍內；C3和C4，C5規定了一個D2D對只能復用一個CUE的頻譜資源，反之亦然；C6和C7表示CUE和D2D傳輸功率的限制范圍。

求解式(4)的最優解，就是將式(4)轉化為最大二分圖匹配問題，然后求出最優解。但是式(4)是一個混合整數的問題，屬于NP難題，求解困難。在性能損失很小可忽略不計的前提下，本文提出一種資源分配算法1-D search，將凸問題轉化為非凸問題，然后利用松弛的方法忽略次要干擾，降低算法的復雜度。與文獻[13]的資源分配算法2-D search相比，1-D search提高了頻譜資源的利用率，同時降低了最優匹配對的搜索時間，為5G的綠色通信和低時延提供了借鑒。

2 資源分配算法

要降低式(4)的搜索范圍，首先要對用戶中斷概率進行研究，然后降低匹配CUE集合的區間范圍，對那些不符合要求的共享頻譜對進行削減，這樣就降低了搜索范圍。本文分3步解決該問題。

2.1 1-Search降低搜索范圍

定義第j個D2D的復用CUE頻譜資源的集合為

(5)

當且僅當傳輸功率和中斷功率滿足上訴要求時，i∈Cj， 即存在i可以讓第j個D2D鏈路復用；如果任何傳輸功率和中斷概率都不能滿足上訴要求，則第j個D2D鏈路沒有可以復用的CUE的頻譜資源，則將這個鏈路刪除。這樣在求解優化問題時，搜索范圍大大降低，從而簡化優化問題。

(1)求解中斷概率

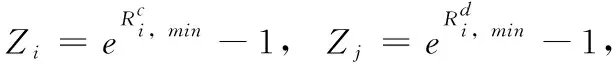
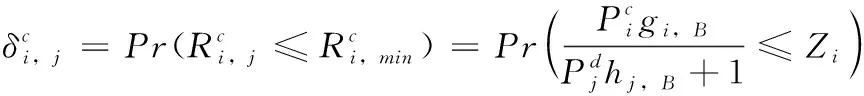
(6)

在實際通信中，D2D傳輸端到BS的干擾是遠遠大于CUE通信的其它噪聲干擾的，同理CUE到D2D接收端的干擾也是遠遠大于其它噪聲干擾[9]。因此式(6)簡寫如下

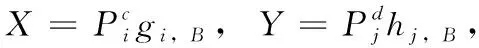
根據gi,B，hj,B的概率密度函數，通過聯合概率分布可求得

(7)

相比2-D search，1-D search忽略次要干擾的影響，對整個計算結果的影響幾乎可以忽略不計。在算法分析過程中，不僅大大簡化了式(6)的計算過程，對整個優化方程的計算難度也降低了，同時復用資源對的搜索速度也加快了。

(2)尋找可行區域

將中斷概率值式(7)帶入集合Cj式(5)可得

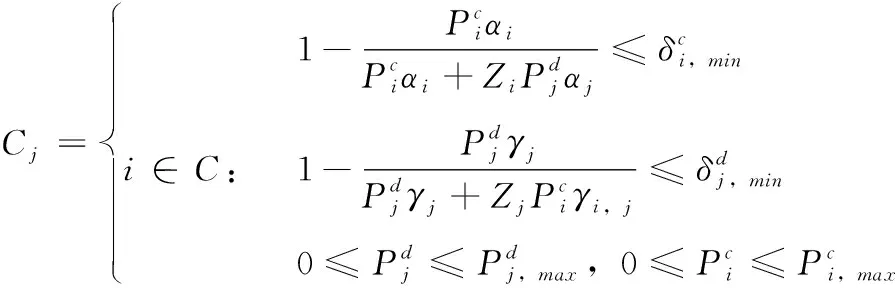
(8)

化解可得滿足中斷概率要求的傳輸功率的可行區域

(9)

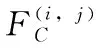
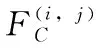
(10)

通過幾何圖形的線性關系，將上述多變量的式(9)轉化為只與信道參數和最大中斷概率有關的式(10)。因此1-Search可以降低共享頻譜對的搜索范圍，避免了算法計算過程中復雜的指數問題，非線性問題轉變為簡單的線性問題，不僅可以降低系統搜索時間，同時降低傳輸功率對匹配對的影響。

2.2 求解系統能效

假設給定一個D2D鏈路，它就會在集合Cj找到一個與該D2D相匹配的CUE，則它的能效表示為

則D2D鏈路的能效為

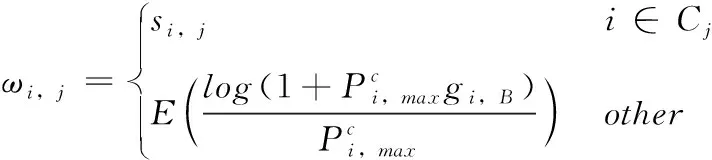
(11)

從式(11)可以看出：當i?Cj時，第j個D2D鏈路沒有和任何CUE共享頻譜資源，因此，ωi,j表示的能效為蜂窩鏈路的能效；當i∈Cj時，存在CUE與之共享頻譜資源，那么si,j就表示CUE和D2D的復用能效，式(4)簡化為

(12)

通過求解上述優化問題，就可以得到有效的復用對(i,j)。因此式(4)就簡化為式(12)。由于該問題的中斷概率以及統計信道參數都為變量，所以求解較困難。因此需引入兩個指數變量的引理[20]：

引理1 隨機變量X和Y都服從指數分布，X～exp(α1)，Y～exp(α2)， 所以

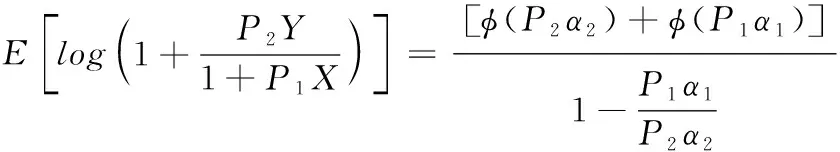
(13)

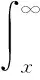
因此可以將能效計算式(11)化解為

(14)

2.3 最佳匹配方案

推導出系統能效值EE的計算方法之后，利用匈牙利算法對CUE和D2D鏈路進行能效最優配對，找出最佳匹配方案。具體算法見表1。

表1 算法1

根據引理2可知：和應滿足下面條件

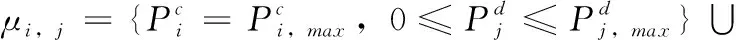
μi,j為蜂窩鏈路和D2D鏈路的發射功率的取值范圍。

3 仿真分析

仿真場景如圖2所示，D2D對用戶的數目M=4，蜂窩用戶的數目N=4，仿真參數見表2。

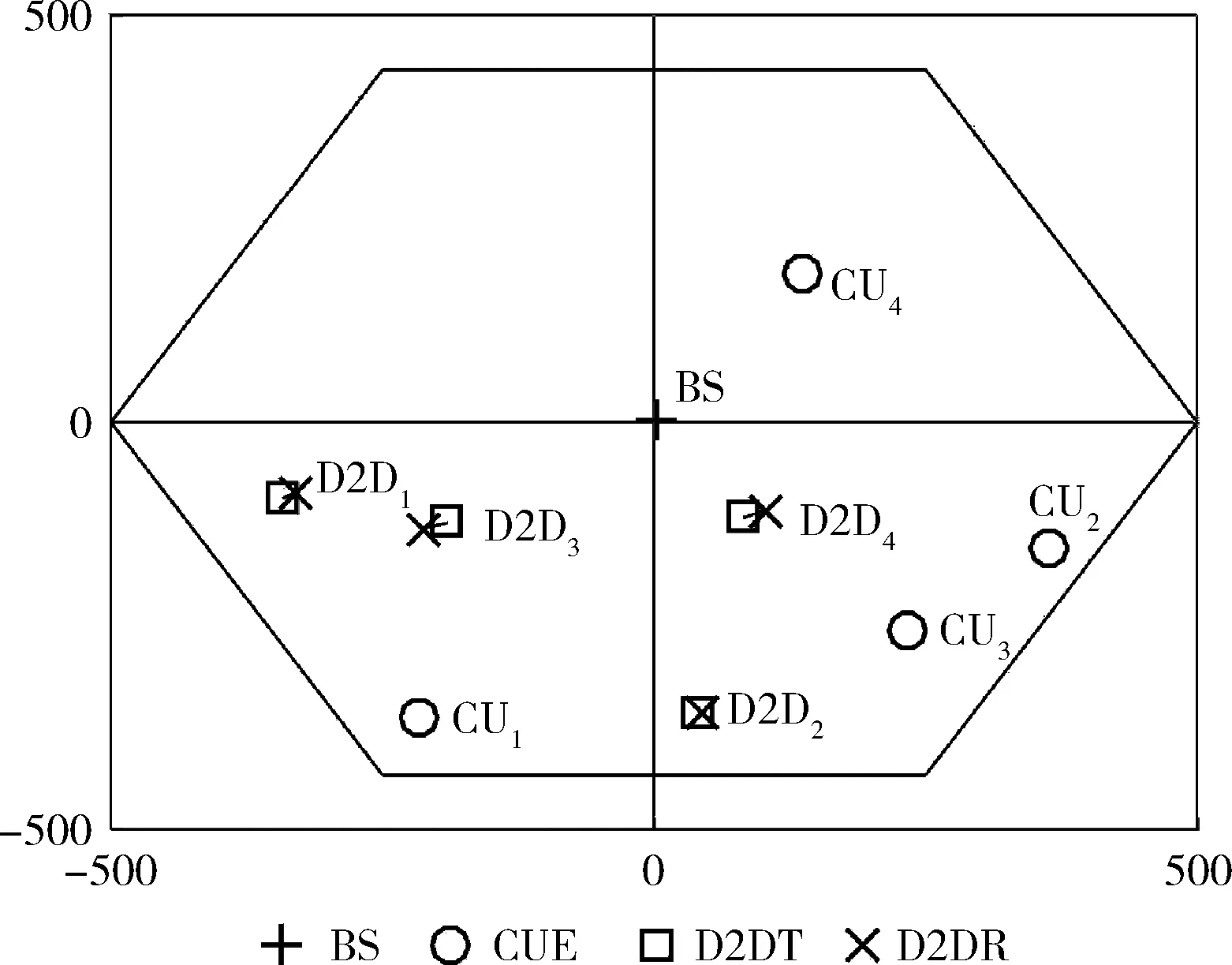
圖2 用戶節點

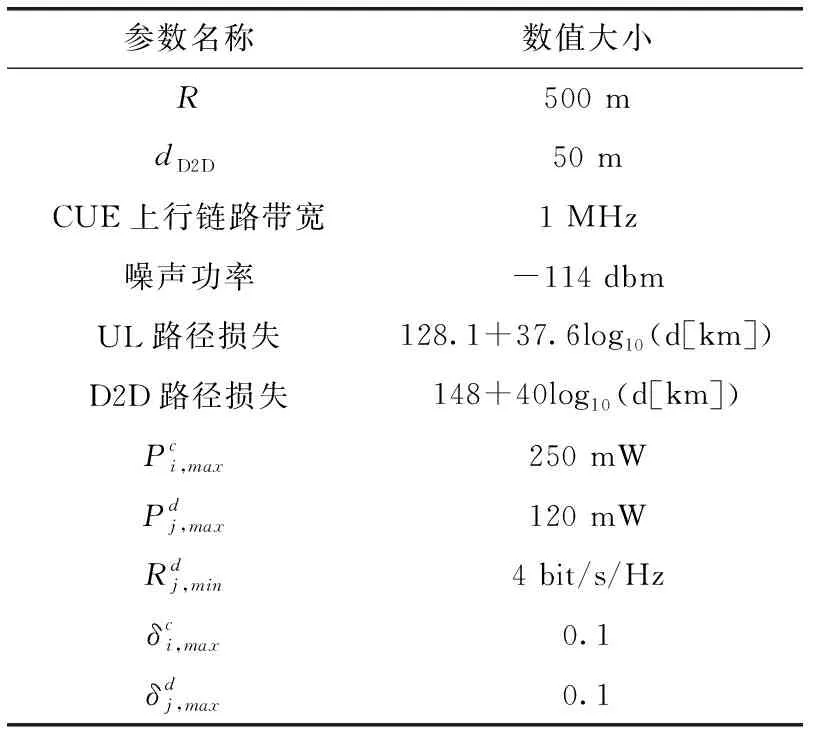
參數名稱數值大小R500 mdD2D50 mCUE上行鏈路帶寬1 MHz噪聲功率-114 dbmUL路徑損失128.1+37.6log10(d[km])D2D路徑損失148+40log10(d[km])Pci,max250 mWPdj,max120 mWRdj,min4 bit/s/Hzδci,max0.1δdj,max0.1

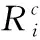
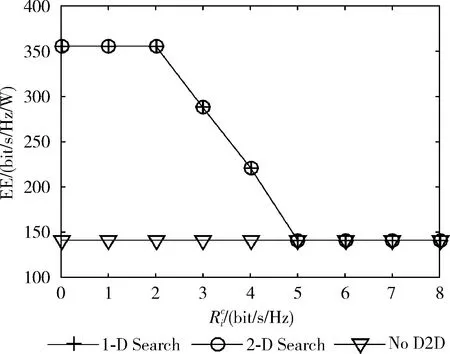
圖3 1-Search和2-Search系統能效EE對比

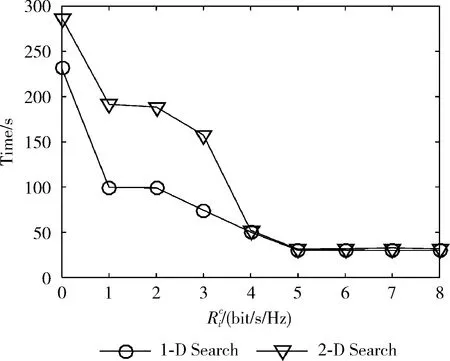
圖4 1-Search和2-Search搜索時間對比

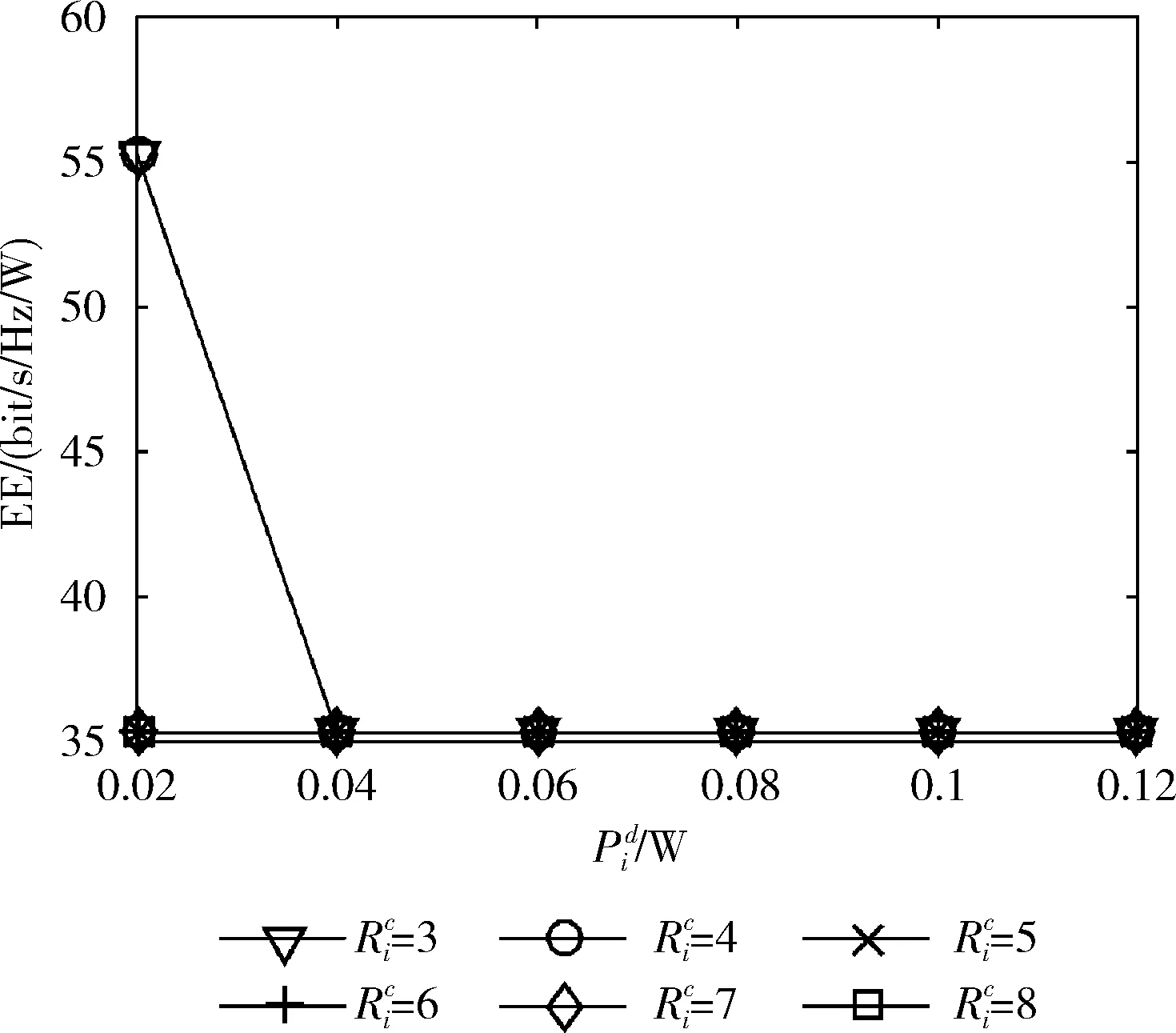
圖5 D2D傳輸功率與能效EE的關系

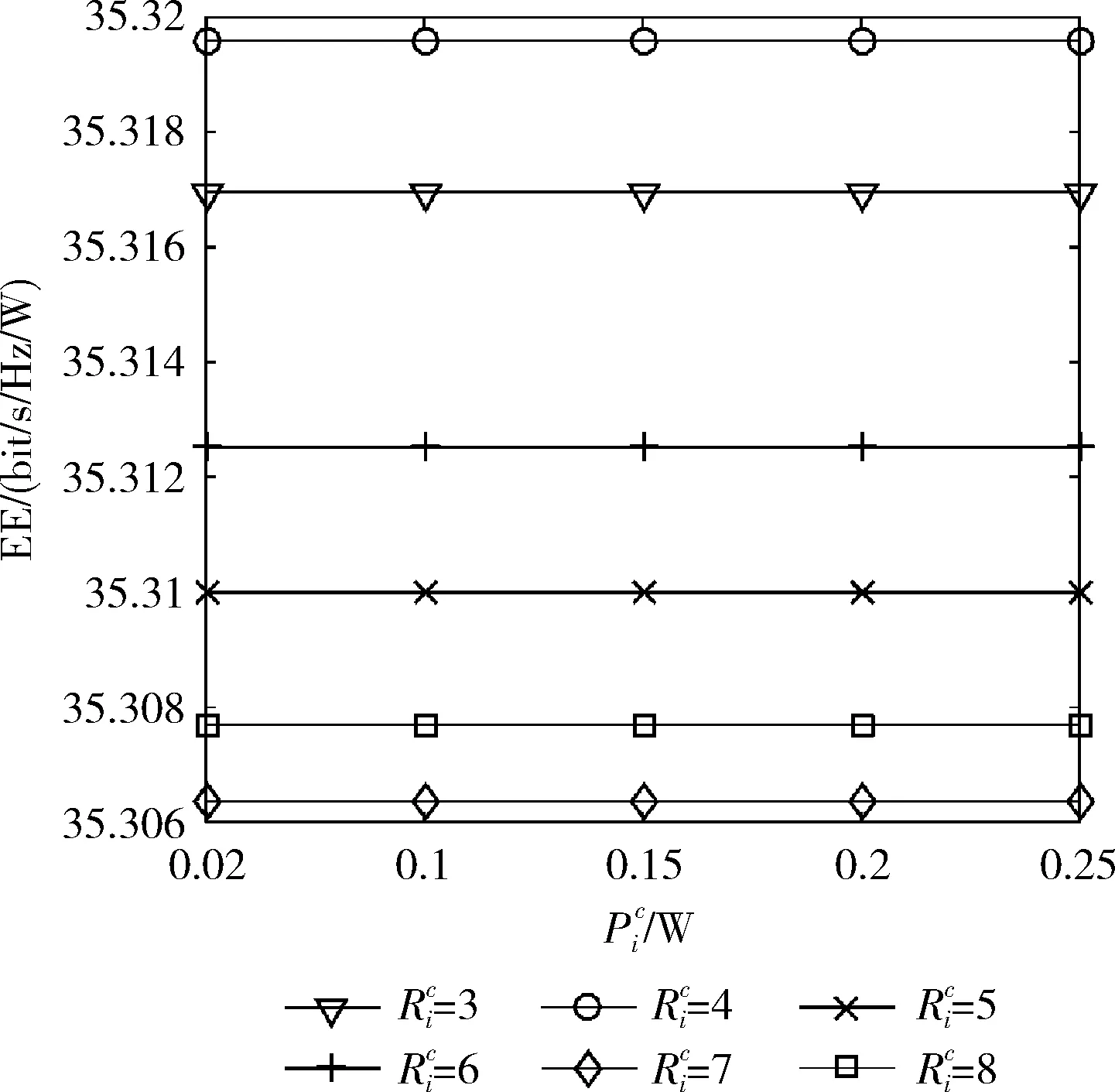
圖6 CUE傳輸功率與能效EE的關系

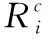
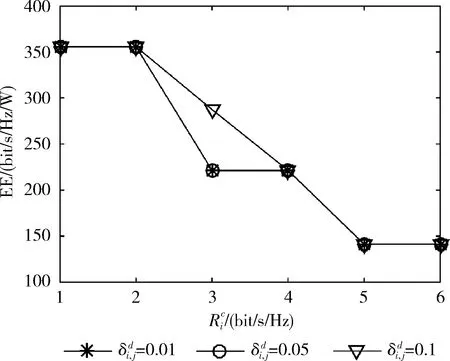
圖7 D2D中斷概率與能效EE的關系

圖8 CUE中斷概率與能效EE的關系

圖9 D2D通信距離dD2D與D2D能效Ej的關系

4 結束語

利用D2D通信技術可以提高頻譜利用率，增加系統容量，但是巨大的用戶接入量會消耗大量能量，同時也會對蜂窩用戶產生干擾。本文在保證用戶QoS和傳輸速率的條件下，提出的一種啟發式算法。其目的有兩個：一是提高系統能效，擴大網絡吞吐量；二是降低D2D用戶的匹配范圍，縮短匹配時間。仿真結果顯示，本文提出的算法能夠提高系統性能，實現上述兩個目的。