基于小波分析的分數階系統辨識

馮衛衛

摘? 要：分數階系統是整數階系統的進一步發展，更適合于描述控制系統。提出了一種分步響應系統參數辨識的方法。該方法利用小波函數積分運算矩陣將分數階微分系統方程轉化為代數方程，用包含小波積分運算矩陣的方程表示待辨識系統的輸出和輸入。通過尋找最小值之間的區別實際的輸出部分系統和識別系統的輸出，獲得最優解，分數微分方程系統的參數識別問題轉化為尋找最優解的問題。該方法可以同時識別分數階系統的系數和階數。此外，該方法避免了直接對輸入和輸出數據微分的復雜計算，簡化了輸入和輸出信號。

關鍵詞：分數階系統;參數辨識;運算矩陣;分數階微積分

中圖分類號：N945.1 文獻標志碼：A? ? ? ? ?文章編號：2095-2945（2020）10-0005-04

Abstract： Fractional order system is the further development of integer order system， which is more suitable for describing control system. A method for parameter identification of step-by-step response system is proposed. In this method， the fractional differential system equation is transformed into an algebraic equation by using the wavelet function integral operation matrix， and the output and input of the system to be identified are represented by the equation including the wavelet integral operation matrix. By finding the difference between the minimum value， the actual output part of the system and the output of the identification system， the optimal solution is obtained， and the parameter identification problem of the fractional differential equation system is transformed into the problem of finding the optimal solution. This method can identify the coefficients and orders of fractional order systems at the same time. In addition， this method avoids the complex calculation of the differential of input and output data directly， and simplifies the input and output signals.

Keywords： fractional order system; parameter identification; operation matrix; fractional calculus

1 概述

分數階系統是基于分數微積分理論建立的數學模型。分數階微積分以加權的形式考慮了函數的全局信息，因此在很多方面分數階系統可以更準確地描述實際系統的動態響應。特別是對于一些實際的復雜系統，分數階微積分方程建模的應用比整數階系統模型更精確。例如，在軍事、物理、通信、電子、計算機等復雜的比例系統中，分數系統可以提供更完善的數學模型，以考慮系統中不可忽視的分形現象。然而，分數系統的辨識和求解方法一直是數學家們努力研究的主要課題。分數階微積分的早期階段出現的發展和計算工具的落后分數微積分，雖然計算機技術發展迅速，應用分數階微積分的場景也更加復雜，導致部分系統的解決方案，識別的復雜性，以及分數微分算子是外地算子，計算過程相對復雜。這些因素增加了求解和識別分數階系統的難度。因此，有必要尋找一種有效的、簡化的解決方案，辨識過程方法是促進分數階系統發展的必要手段。

分數階系統的研究主要包括兩個方面：分數階系統的求解和分數階系統的辨識。分數階微分方程的解及其數值解是分數階系統分析的理論基礎。對于分數階微積分方程的解析解不僅難以獲得，而且在實際應用中意義也不大，因此數學家們給出了自己求解數值解的方法。首先，研究了具體分式微積分方程的解。例如，Wyss W[1]給出了布萊克-斯科爾斯方程的一個完整解。Liu F、Anh v[2]等獲得了求解分數階佛克-普朗克方程的方法。對于Diethelm K[3]等人的Adams類分數階微分方程，采用預測修正法得到分數階微積分的數值解。對于分式擴散方程，即物理領域中的Wyss W，研究了特定條件下的分式擴散波動方程及其相關屬性。Mainardi F等給出了復平面上格林函數的一般表達式，在卡普托分數階微積分定義的基礎上，求出分數階擴散波動方程的解。此外，Benson D A等給出了分數階水平散射方程基于分數階穩定誤差函數的解析解。

近年來，利用運算矩陣求解分數階微積分方程的方法受到許多研究者的關注，如塊脈沖函數運算矩陣、小波變換運算矩陣、帽函數運算矩陣等。

雖然在過去的幾十年里，線性或非線性的分數階微積分已經出現在許多領域，但是由于分數階微積分的歷史悠久，幾乎不可能對分數階系統進行建模。因此，基于系統輸入和輸出數據的參數辨識方法是建立分數階系統模型的有效方法。

分數階系統的參數辨識方法分為時域辨識和頻域辨識兩類。為了識別分數階系統的時域，可以將其分為單輸入單輸出分數階系統識別和多輸入多輸出分數階系統識別兩類。在SISO分數階系統時域辨識的研究中，Rachid等[4]給出了基于方程誤差和分數階泊松濾波器輸出誤差的時域辨識方法。Malti等人[5]利用最優輔助變量法將簡化修正時間系統方法推廣到分數階系統。Hartley等研究了時域連續有序分布系統的辨識方法。此外，正交基理論在控制系統建模和控制中的應用越來越受到重視。該方法的主要思想是通過一系列正交基函數的線性組合來表示傳遞函數，即用一組正交基函數來表示系統，該思想也被用來識別分數階系統。Malti等將kautz型正交基擴展為分數階模式，利用分數階Kauthz函數正交基表示分數階系統，得到基于輸出誤差的時域辨識方法。Aoun等人使用分數階正交基函數Laguerre描述分數階系統，給出了時域辨識方法。由于分數階的非本地特點micro-integral運營商和長記憶特性，時域計算需要大量的歷史數據，數據的大型和復雜的時域識別帶來了很大的不便，分數階系統的時域識別，以及頻域識別可以避免困難，因此分數階系統的頻域識別也備受關注。

2 Haar小波與分數階積分運算矩陣

2.1 分數階微積分定義

RL分數階微積分定義：

（2-1）

其中？酌為階次，？酌>0。

與Riemann-Liouville定義相比，Caputo定義更加方便描述分數階微分方程的初值問題，Caputo定義：

（2-2）

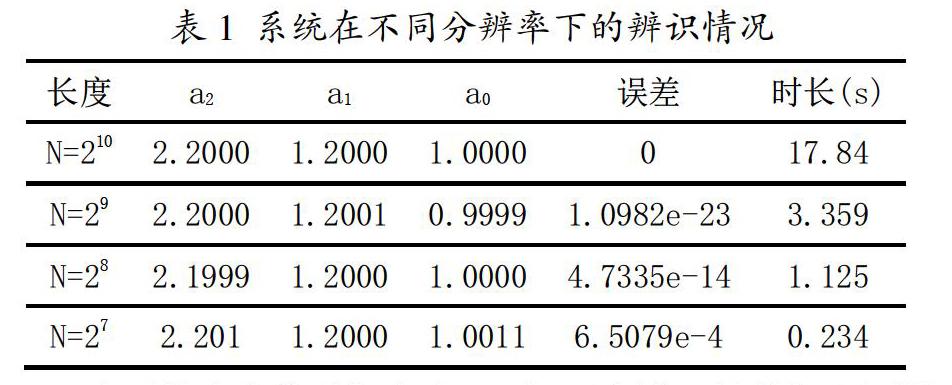
其中，？酌>0，n-1<？酌

Caputo定義的積分定義有一個重要性質：

（2-3）

其中，t>0，n-1<？酌

2.2 Haar小波分數階積分運算矩陣

Haar小波為正交函數，定義：

（2-4）

其中，n=2j+k，0？燮k？燮2j，j？叟0，k，j∈Z。

此外，

（2-5）

任意屬于區間L2[0，b]的函數f（t）都可以用Haar小波展開為：

其中Haar系數ri，i=0，1，2可以由下面的公式推導出：

對于式（2-6）的無限項和，在實際計算中，我們可以用有限項和來近似表示：

其中，N=2j，T代表矩陣的轉置，RN=[r0，r1，...，rN-1]T為系數向量，HN（t）=[h0（t），h1（t），...，hN-1（t）]T為Haar函數向量。我們需要N個方程來求得系數向量。

定義N階Haar矩陣為：

根據現有知識，我們可以根據塊脈沖函數積分運算矩陣，自行推導出Haar小波積分運算矩陣，記P為？琢階Haar小波積分運算矩陣，塊脈沖？琢階積分運算矩陣為F？琢，得到：

[6]? ?（2-10）

至此我們就得到了Haar小波運算矩陣。

3 小波分析的多分辨率分析

多分辨率分析是指將函數表示為具有時間分辨率和頻率分辨率的分量組合。也就是說，一個函數被映射到一系列嵌套的近似空間。一個空間通過兩次連續的分解，可以逐步形成一組包含子空間的集合。空間分解符號如下：

（3-1）

上式中Wn-1可以看作是低分辨率函數Vn-1去近似高分辨率函數Vn時，所丟失的細節部分，？茌為正交和的形式。每個空間都可以這樣去分解，尺度函數構成近似V空間的基，小波函數構成細節W空間的基，對任意空間分解得：

（3-2）

將之運用到空間L2（R）上，則空間中的任意函數f可以分解為：

其中，f0∈V0，wl∈Wl且0？燮l<0。

由前面的式（2-8）小波變換近似得出，信號可以近似分解為：

（3-4）

小波變換后，將信號f（t）的系數分為低頻部分和高頻部分。通常，低頻部分被認為是原信號的近似值，特別是在原信號有噪聲的情況下，低頻部分具有降噪效果。因此，在每一層中，低頻系數只是這一層系數的一半。通過小波變換對輸入和輸出信號進行分解重構，將系統辨識的過程轉化為小波系數的辨識。我們逐層拋棄高頻分量的系數。即按比例減少N的值，系統辨識所涉及的數據量將減少2n倍，其中N為分解層數。這種思想既可以對信號進行降噪處理還可以加速分數階系統的辨識。

為了在對小波系數重新采樣時保證信號不失真，不能對信號進行分層。也就是說，N的值不能連續下降。根據對原始信號的頻譜分析，在拋棄信號高頻成分的小波系數時，需要保證新信號滿足采樣定理。如果N值太小，新信號就不能準確地表示原信號，識別結果也就沒有意義。最終的層數由近似分量和原始信號的相關系數決定，一般不能小于98%。

4 分數階系統辨識

對于一般初始狀態為零的分數階線性系統：

（4-1）

其中f（t）和y（t）為系統的輸入輸出數據，b1，b2，b3為任意正數，且b1>b2>b3。

利用小波變換分解系統輸入輸出：

（4-2）

（4-3）

對等式（4-1）兩邊做b3次積分運算，并將式（4-2）、式（4-3）代入，得到：

（4-4）

即：

（4-5）

對于上式中的系數a3，a2，a1和階次b3，b2，b1都是需要求解的，但是直接求解必然會碰到非線性優化問題，所以在這里先是假定分數階微積分的階次是已知的，再在這樣的情況下去求解系數參數。

上式（4-5）經過整理的得到：

（4-6）

假設? ? ? ? ? ? ? ? ? ? ? ? ? ?，? ? ? ? ?，

，那么式（4-6）可以簡化為：

（4-7）

利用最小二乘法可以求得系數矩陣x的值，從而獲得系數參數：

（4-8）

上面都是在假定階次已知的情況下的，但是階次并非一定是我們剛剛假定的，所以，我們需要讓階次在已定范圍之類變化，通過比較系統輸出和辨識出來的系統輸出之間的誤差，找到誤差最小的一組解，完成辨識。

5 例證

5.1 對理想狀態下的分數階系統進行辨識。

對于系統：

（5-1）

令? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?，在零狀態下，我們對系統輸入單位階躍響應，得到輸出響應，根據輸入輸出數據，進行辨識。在辨識過程中，我們對輸入輸出信號進行從長度為210到27的小波展開，然后看各組辨識誤差，辨識誤差以及辨識耗時如表1所示。

當系統響應信號長度為27時，用來辨識的數據和原始數據的對比，如下圖1所示。

從表1中，我們可以看出成倍的增大低頻頻率雖然增大了辨識誤差，但是仍然是可以接受的誤差范圍之類，而且系統辨識的耗時是可以看到降低了很多的，尤其是針對數據量非常龐大的情況下，小波分析的多分辨率特點非常實用。

5.2 對含有噪聲的分數階系統進行辨識

小波分析除了上面說到的可以加快系統辨識過程，還可以對含有噪聲的系統進行降噪，具有很強的抗干擾能力，尤其是在實際的系統中，噪聲參雜在輸出信號中是難免的事，下面對含有噪聲的信號進行辨識。

針對式（5-1）提出的系統，我們先對其輸出信號進行加噪處理，然后用小波分析處理加噪后的信號，對降噪后得到的信號進行分數階系統辨識，看降噪后的信號與原信號之間的誤差以及未降噪信號與原信號之間的誤差，兩者進行比較，看小波分析降噪是否可行。

對輸出信號添加40dB的高斯白噪聲，對含有噪聲的不同長度的輸出數據進行系統辨識，得到的參數和耗時如表2所示。

對含有噪聲的信號進行小波分解，對分解后的降噪信號進行分數階系統辨識，辨識過程情況如表3所示。

在辨識經過小波分析降噪處理后的系統輸出時，的確比降噪前的辨識更加精準。

6 結束語

文中提出一種基于小波分析的分數階系統辨識方法。該方法通過對輸入信號和輸出信號的小波系數進行重采樣，減小了輸入信號和輸出信號的數據量，提高了分數階系統辨識的速度。通過比較不同小波頻率辨識過程驗證了小波分析多分辨率的可靠，通過比較含噪和不含噪的信號的辨識過程，說明了小波分析降噪的作用。

參考文獻：

[1]Wyss W.The fractional Black-Scholes equation[J].Fractional Calculus & Applied Analysis， 2000，3（1）：51-61.

[2]Liu F， Anh V， Turner I. Numerical solution of the space fractional Fokker-Planck equation[J]. Journal of Computational & Applied Mathematics， 2004，166（1）：209-219.

[3]DIETHELM， FORD， N. J， et al. Algorithms for the fractional calculus： A selection of numerical methods[J]. Computer Methods in Applied Mechanics & Engineering， 2005，194（6）：743-773.

[4]MALTI， Rachid， VICTOR， et al. Advances in System Identification Using Fractional Models[J]. Journal of Computational & Nonlinear Dynamics， 2008，3（2）：764-786.

[5]Malti R， Aoun M， Oustaloup A. Synthesis of fractional Kautz-like basis with two periodically repeating complex conjugatemodes[C]//International Symposium on Control，2004.

[6]孟霄.基于運算矩陣的分數階系統辨識及控制器參數整定[D]. 南京信息工程大學，2017.