ABAQUS強度折減法在邊坡穩定性分析中的適用性研究

方旭東 余以強 金奇

摘? 要：基于“四好農村路”建設邊坡穩定性分析需要，開展有限元分析軟件ABAQUS結合強度折減技術在邊坡穩定性分析中的適用性研究。通過建立邊坡有限元數值分析模型及Geo-SLOPE邊坡極限分析模型進行對比驗證，邊坡安全系數均接近1，塑性滑裂面位置和形狀非常接近。結果表明，基于ABAQUS強度折減法的邊坡穩定性分析結果準確可靠，將邊坡臨空面處邊坡頂點位置選取為特征點且依據其水平位移與抗剪強度折減系數之間的關系曲線來確定邊坡安全系數簡單可行。

關鍵詞：ABAQUS;強度折減法;邊坡穩定性

中圖分類號：U417 文獻標志碼：A 文章編號：2095-2945（2020）10-0161-03

Abstract： Based on the needs of slope stability analysis of "Four-merit Rural Road" construction， the applicability of finite element analysis software ABAQUS combined with strength reduction technology in slope stability analysis is studied. Through the establishment of slope finite element numerical analysis model and Geo-SLOPE slope limit analysis model， the safety factor of slope is close to 1， and the position and shape of plastic slip surface are very close. The results show that the result of slope stability analysis based on ABAQUS strength reduction method is accurate and reliable， and it is simple and feasible to select the vertex position of the slope at the open surface of the slope as the characteristic point and determine the safety factor of the slope according to the relation curve between the horizontal displacement and the shear strength reduction factor.

Keywords： ABAQUS; strength reduction method; slope stability

引言

隨著“四好農村路”理念的提出，全國各省市都在黨中央號召下大力加快新建改建四好農村路，伴隨建設的深入及農村山區地形地貌的復雜性，農村公路邊坡的安全建設顯得尤其重要。在“四好農村路”設計、施工、養護與運營過程中，有必要建立農村公路邊坡管理機制，對邊坡穩定性進行分析與管控，確保公路安全通行。

目前為止，邊坡穩定性的分析方法主要包括傳統分析方法和數值分析方法兩大類別：傳統分析方法主要表現為極限分析法、極限平衡法及滑移線法等;數值分析方法主要表現為有限元法、有限差分法、快速拉格朗日分析法、邊界元法、離散元法及無單元法等[1]。

基于傳統分析方法對邊坡穩定進行分析時，破壞分析與變形分析不具有相關性，分別將坡體假定為理想剛塑性和線彈性，不能真實反映邊坡坡體內應力應變關系，這與實際邊坡失穩情況存在較大出入，傳統分析方法在計算分析邊坡穩定性時存在不足。

基于數值分析方法的邊坡穩定性分析是建立在計算機技術實質發展得以實現的，數值分析方法不僅計算效率高而且可以考慮材料、邊界和幾何條件的非線性，受到廣大學者的青睞。同傳統分析方法相比，主要區別和優勢表現為：（1）不需要對滑裂面形狀和位置做出假定;（2）力的平衡得到滿足，不僅可以考慮邊坡土體內部應力-應變關系，而且可以分析邊坡坡體的破壞發生和發展過程;（3）在兼顧邊坡土體非均勻性的同時，還能兼顧復雜地質地貌邊坡;（4）能夠分析計算土體與支擋結構間相互作用等。

有限元分析方法作為數值分析方法的典型，是當下最廣為使用的數值分析方法，相較于有限差分法用于邊坡穩定計算分析少、邊界元法需事先掌握控制微分方程基本解且不能處理大變形問題、離散元法乏于阻尼選取和迭代收斂性等缺點，有限元分析方法不僅能夠應用于幾乎全部計算領域，而且在邊坡穩定性計算分析方面尤為成熟。

ABAQUS作為達索SIMULIA公司開發的一款有限元軟件，是功能強大的國際大型通用非線性有限元軟件之一，不僅可以模擬非常復雜的工程結構，而且具有能夠豐富真實表現土體性狀的本構模型庫，在模擬非線性巖土體方面優勢顯著。ABAQUS人機互動簡單，建模方便，可以靈活、準確地建立初始應力狀態，具有二次開發功能，在巖土工程方面有很強的適用性，適用于邊坡穩定性計算分析。

綜合對比分析各種邊坡穩定性分析方法，兼顧有限元數值分析方法優勢和工程實用性，本研究基于國際大型通用非線性有限元軟件ABAQUS融合強度折減方法開展邊坡穩定性進行計算與分析，研究其在邊坡穩定性分析中的適用性，為“四好農村路”邊坡建設服務。

1 有限元強度折減法理論

強度折減方法由Zienkiewicz[2]于1975年基于強度儲備概念最早提出，但因為早期受限于計算機技術，沒有廣泛應用。

基于計算機技術和有限元理論的發展成熟，學者們提出融合有限元技術和強度折減方法的有限元強度折減理論，定義抗剪強度折減系數：在邊坡土體所受外荷載不變的情況下，邊坡土體所能承擔的最大抗剪強度與邊坡土體實際產生的剪應力之比。當邊坡內所有土體抗剪強度發揮程度一致時，折減系數等同于傳統意義上的邊坡整體穩定安全系數Fs，與極限平衡分析法中給出的穩定安全系數概念等同，折減后的抗剪強度指標如式1、式2所示。

式中：c、？漬為土體抗剪強度指標;cr、？漬r對應最大折減系數抗剪強度指標;Fr為折減系數即邊坡整體安全系數。

2 有限元強度折減法失穩判據

采用有限元強度折減法計算邊坡穩定性的關鍵在于確定邊坡是否處于極限平衡破壞狀態，文獻[3-6]表明，目前存在的用于判斷邊坡是否處于失穩狀態的判據主要有三種：

（1）基于有限元計算程序是否收斂以判斷邊坡是否處于失穩狀態，該判據存在過分依賴程序計算收斂性的不足，人為設置在一定程度上尚存影響，不甚廣泛應用。

（2）基于等效塑性應變或者廣義塑性應變是否從坡頂延伸至坡腳形成貫通帶以判斷邊坡是否處于失穩狀態，趙尚毅、鄭穎人等[3]認為只有滑動面上所有點的應變均超過極限才能判定邊坡失穩，塑性區貫通是邊坡失穩的必要非充分條件。

（3）依據邊坡表面某一特征點位移是否發生突變以判斷邊坡是否處于失穩狀態，該判據與工程邊坡實際失穩現象吻合，基于特征點位移與折減系數關系曲線確定邊坡安全系數較為合理，文獻[7]認為將邊坡臨空面坡頂位置視作特征點判定邊坡是否失穩可靠。

綜合以上分析，本研究利用有限元分析軟件ABAQUS融合強度折減法計算邊坡穩定性時選擇判據三作為邊坡失穩與否的依據。

3 ABAQUS中強度折減法實現與驗證

依據強度折減法理論，結合ABAQUS場變量功能，在邊坡模型建立好后通過設置場變量（即為折減系數）實現邊坡土體抗剪強度指標粘聚力和內摩擦角的折減，具體分析步驟如下：（1）建立邊坡模型;（2）設置材料參數并定義場變量以及土體抗剪強度指標隨場變量的變化關系;（3）建立分析步和施加荷載;（4）編輯模型keyword并提交計算;（5）提取邊坡坡頂位移與場變量數據，確定邊坡安全系數Fs。

為了便于比較和保證計算結果的準確性，作者利用Dawson[8]等所用計算分析均質土坡模型來驗證ABAQUS有限元強度折減方法可行性和精確度。該模型理論邊坡安全系數為1，已被很多方法驗證，諸多方法計算結果都非常的一致。利用該邊坡模型驗證ABAQUS有限元強度折減方法的合理性具有一定的說服力，模型參數如表1所示。

旨在更全面地確保ABAQUS強度折減方法的精度，本研究還通過全球知名巖土工程分析軟件GeoStudio邊坡分析模塊建立邊坡分析模型并基于其多種極限分析方法進行計算分析，計算結果見如表2。由表2可知，Morgenstern-Price、Bishop、Janbu、Spencer計算所得邊坡安全系數均近似為1，計算結果較為一致，適用于對比分析ABAQUS強度折減法計算結果。

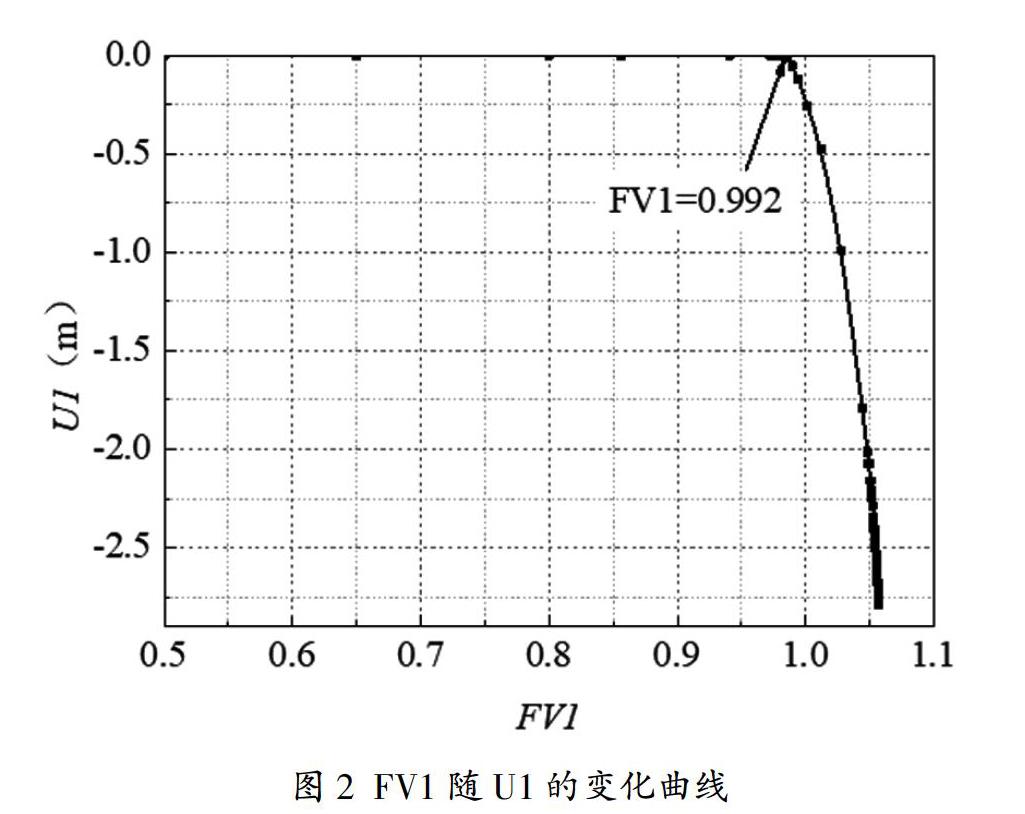
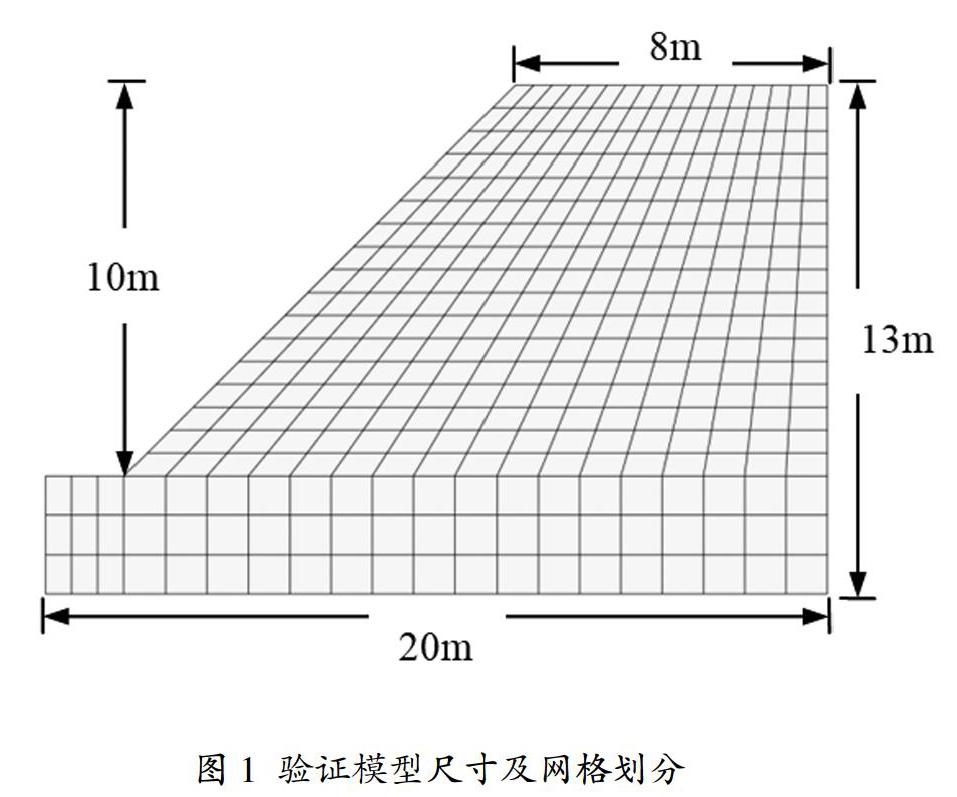
鑒于對比的統一性，依據前述分析步驟建立與Dawson所用完全一致的邊坡分析模型并進行網格劃分，邊坡模型尺寸和網格劃分情況如圖1所示。模型計算分析后，基于邊坡失穩判據三繪制邊坡頂點水平位移U1-折減系數Fr即場變量FV1關系曲線并識別U1突變位置隨即獲取邊坡安全系數。

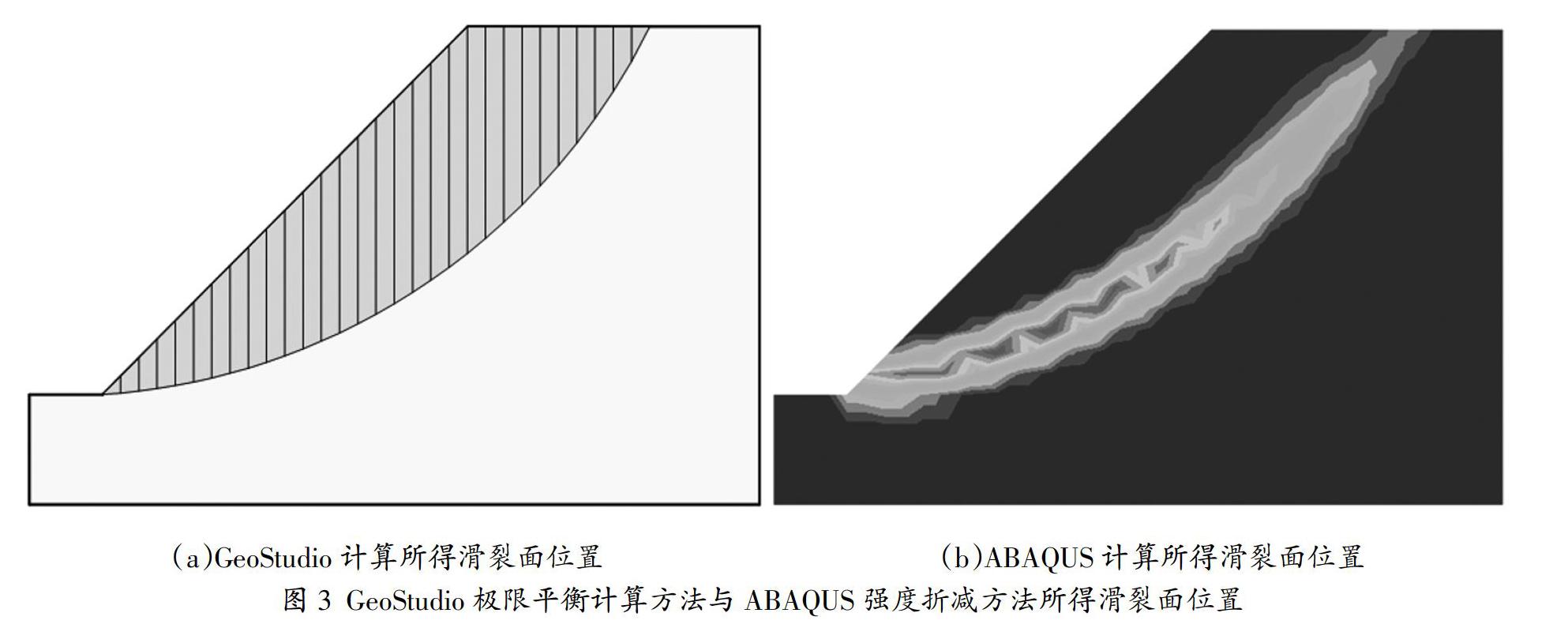
由圖2可知，有限元強度折減法計算所得邊坡安全系數為0.992，與模型理論安全系數和極限分析模型所得安全系數非常接近，均近似為1。與此同時，從圖3能夠發現，有限元計算模型與極限分析模型計算所得滑裂面位置和形狀也非常吻合，計算結果很理想。

4 結束語

綜上所述，ABAQUS邊坡有限元數值分析模型及Geo-SLOPE邊坡極限分析模型計算結果表明，邊坡安全系數均接近1，塑性滑裂面位置和形狀非常接近。利用有限元數值分析軟件ABAQUS融合強度折減方法計算所得邊坡安全系數具有較高的準確度，能夠準確反映邊坡坡體內部應力應變關系，可用于邊坡穩定性的計算分析，服務于“四好農村路”邊坡建設。

參考文獻：

[1]蔡路軍，朱以文，馬建軍.邊坡穩定性數值分析方法述評[J].西部探礦工程，2006，18（10）：268-270.

[2]Zienkiewicz， O C， Humpheson C， Lewis R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics[J]. Geotechnique， 1975，25（4）：671-689.

[3]趙尚毅，鄭穎人，張玉芳.極限分析有限元法講座——Ⅱ有限元強度折減法中邊坡失穩的判據探討[J].巖土力學，2005，26（2）：

332-336.

[4]金曉杰.基于有限元強度折減法的南海某典型峽谷區斜坡穩定性評價[D].青島：青島理工大學，2013.

[5]吳伯建，朱珍德，顧祖軍.有限元強度折減法進行土坡穩定分析的精度研究[J].水利與建筑工程學報，2013，11（1）：17-21.

[6]蔡路軍，馬建軍，周大華，等.基于ABAQUS的邊坡失穩綜合判據法[J].武漢科技大學學報，2011，34（5）：354-358.

[7]高志輝.有限元邊坡穩定參數敏感性分析[D].北京：北京工業大學，2007.

[8]Dawson， E M， Roth W H. Slope stability analysis with FLAC[C]//FLAC and Numerical Modeling in Geomechanics （Proceedin

gs of the International FLAC Symposium on Numerical Modeling in Geomechanics， Minneapolis， Minnesota， September.1999：3-9.