內河航道局部縮窄段交通運行狀態仿真分析

孔 莊,項雨略,廖 鵬，陳 虹

(1.中交上海航道勘察設計研究院有限公司，上海 200120；2.東南大學 交通學院,江蘇 南京 211189)

內河航運具有運量大、能耗低、污染小等特點，因而可有效緩解流域土地資源緊張和大宗物資陸運壓力，對節約能源和減少污染物排放都具有積極作用。上海國際航運中心就明確提出要形成結構優化的現代化港口集疏運體系，打造連接蘇浙、對接洋山深水港區集裝箱運輸的上海內河航道網[1]。然而，上海地區土地資源緊張，河道沿線廠礦企業、跨河建筑物密布，不少通航河流局部航段受到邊界限制而不能滿足雙向通航，形成航道局部縮窄段或瓶頸段，制約著航道的通航安全和通過能力。

分析航道局部縮窄段的交通運行狀態與通過能力，是航道規劃、設計與運營中的重要基礎性工作。目前已有的經驗公式有諸多假定和經驗系數，對航行規則、船型及交通流等參數的差異性考慮較少[2-3]；排隊模型側重于研究宏觀的交通流規律，對于船舶個體狀態的分析有所局限[4]；采用仿真的方法模擬船舶行為[5-8]，建立類似單線船閘開通閘的交通模型，則能夠更細致地考慮諸多復雜的要素，量化各項交通運行指標，預測通過能力，以便從航運需求、通航安全、交通組織和服務質量等方面采取高效集約的方案改善通航條件。

本文以上海大浦線航道為例，針對該航道某局部縮窄段改建方案的船舶交通運行狀態，根據航道單線交替通航特征設計仿真模型，仿真分析不同條件下縮窄航段的交通運行狀態，預測縮窄段的最大通過能力，對比分析不同條件對縮窄航段運行狀態的影響，供相關規劃和設計參考。

1 仿真模型

1.1 工程背景

大浦線是規劃的長江三角洲地區“兩縱六橫”高等級航道網組成之一，也是上海市“一環十射”高等級航道環線的一部分。航道南北貫穿浦東新區，全長39.3 km，2015年船舶流量27 564艘，是黃浦江以東片區重要的集疏運通道，目前尚未達到規劃的Ⅲ級通航標準。“十三五”期間開展了該航道整治工程的前期研究工作[9]，其中某磁懸浮鐵路跨河橋梁不滿足雙向通航凈寬要求，因橋梁改建存在諸多限制和困難，擬將橋下約280 m航段設計底寬由55 m局部縮窄至27 m，橋梁上下游各設150 m緩沖段和一處錨地候泊區，采用交通信號燈結合人員調度進行單線通航管制(圖1)。

圖1 大浦線航道局部縮窄段示意

1.2 航行規則

受單線通航的限制，航道局部縮窄段具有周期性、方向轉換和集中通過等特征，任意時刻下縮窄段的狀態有3種情況：一是航道空閑，來船可以直接駛入航道；二是航道被另一航向船舶占用，來船必須排隊等待；三是航道已被本航向船舶占用，來船具備進入航道的條件，需要結合另一航向的排隊情況Q控制船舶是否進入的條件。

考慮該局部縮窄段通航的公平和效率，設定2種航行規則：1)基本規則——優先保證公平，船舶先到先過、交替通航，即一旦出現排隊(Q> 0)則該航向入口關閉，盡快為另一航向排隊的船舶提供通行條件；2)管制規則——強制船舶進行一定的等待，待數量滿足一定條件時(Q>Qa)才集中放行，特別是某一航向需求明顯偏大時，集中服務以提高通航效率。

1.3 模型設定

交通仿真建模就是模擬船舶到達并通過航道局部縮窄段的全過程，通過記錄相關數據以統計分析航道交通運行狀態，可將其視為一個雙隊列單服務臺的排隊系統。其中，航行規則決定了一個周期內服務的船舶數量m，船舶到達時間間隔I和通航歷時T決定航道在一個方向上的運行周期S，周期結束則服務另一航向。在低密度交通流下，船流量A一般被認為服從泊松分布，對應到達時間間隔I服從負指數分布。通航歷時T為船舶通過航道的一系列操作所需的時間，由3部分組成：1)航行時間t1，與航道長度L和航速v有關，參考類似航行情況[10]，取v=1.0 ms；2)船舶離岸、啟動和組批等耗費的時間t2，t2值為3～5 min；3)船頭時距t3，集中通過時與船舶的數量m和船舶領域hi有關，借鑒停船視距船舶領域模型[11]，與航速v和船長li相關。

(1)

航道局部縮窄段的實際交通十分復雜，為便于仿真建模，進行如下簡化：1)航道為理想狀態，僅考慮長度和線數的影響，忽略水文、氣象等客觀因素；2)船舶通過局部縮窄段時，航速較低且為勻速；3)候泊區可以提供足夠多的泊位供船舶排隊等待。

1.4 仿真過程

基于航行規則和模型設定，利用元胞自動機原理，將航道交通系統抽象為離散元胞按規則演化[12]，在Matlab平臺上設計了系統仿真框架，包括數據輸入、航行控制和數據更新模塊(圖2)。其中，數據輸入模塊按航道長度建立元胞空間，并根據到船規律和船舶屬性生成船舶列表；航行控制模塊按航行規則和系統狀態判別船舶進入和離開航道的時間，并使航道內船舶保持足夠安全領域下跟馳航行；數據更新模塊計算下一仿真步長時的各元胞運行指標并同步更新，最終映射在航道交通運行狀態的變化中。

為節約模型運行時間，同時減小隨機性帶來的誤差，設置仿真時長30 d，重復運行10次，每隔1 min分別記錄上、下行排隊長度Q和船舶延誤D，每周期結束后統計通過艘數m和運行周期S。

圖2 系統仿真框架

2 結果分析

2.1 運行狀態

為分析不同航運需求下的航道縮窄段交通運行狀態參數，以大浦線航道2015年(工況1)實際船流量和2025年(工況2)、2035年(工況3)預測船流量為例進行仿真試驗。其中，船舶屬性(尺寸、噸位)按設計1 000噸級船型取值，假定2個航向船流量相同，基本規則下仿真運行30 d的結果見表1和圖3。

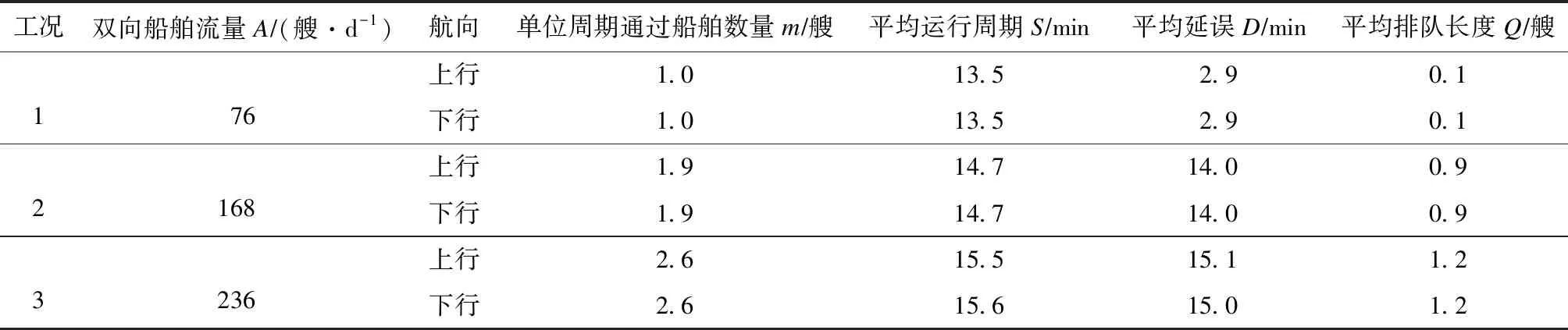
表1 航道運行30 d的狀態參數(基本規則)

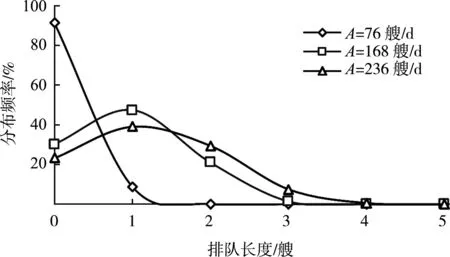
圖3 不同船舶流量下的船舶排隊長度分布

工況1低密度船舶流時，單位周期通過平均艘數為1.0艘，平均排隊長度0.1艘，出現排隊(Q≥1)的頻率僅為8.8%，說明該條件下航道局部縮窄對交通運行狀態影響有限。隨著船流量的增長，各項指標均呈現不同程度的上升，工況3船流量最大時有76.8%的頻率需要排隊，單位周期通過艘數為2.6艘，平均運行周期為15.6 min，表明了通航需求大時，船舶因出現排隊而開始集中通過，此時船舶平均延誤15.0 min(約1個周期)，平均排隊長度1.2艘，需要設置錨地供船舶候泊等待。

進一步分析排隊長度的分布可知，3個工況下的最大排隊長度分別為1、4和5艘，保證率為98%時排隊長度分別為0.8、2.0和2.8艘，因此候泊區設置3～5個泊位即可滿足需求，從而保障船舶的通航安全。

2.2 船流方向分布的影響

上文假定2個航向船流量相同，但實際中受碼頭分布、貨物流向、運轉周期的影響而可能有所不同，以方向分布系數β(β=A單向/A雙向)[13]衡量不同航向船流量的差異，其中，β=0.5表示2個航向船流量相同，β=1.0表示為單向船流。以工況3為例，仿真計算了β在0.5～1.0之間時(雙向總流量相同)采用不同航行規則的航道運行主要指標。

表2以β=0.75(A上行:A下行=3:1)為例給出2種航行規則的航段運行狀態參數，對比β=0.5時的情況(表1，基本規則，工況3)，船流量方向分布影響著航道的運行狀態，船流量較大方向上的平均排隊長度由1.2艘提高到1.7艘，2個方向的總體平均延誤由15.0 min降低到14.1 min。若采用管制規則，由于強制船舶進行一定等待，船舶集中通過的比例得到提高，主要航向(上行)的單位周期通過艘數和平均運行周期相應增加，下行延誤增加6%但上行延誤減少40%，雙向平均延誤由14.1 min減少到10.3 min，雙向排隊總長由2.4艘減少到1.8艘，表明在此條件航段的運行效率得到提升。

表2 β=0.75時航道運行30 d的狀態參數(A=236艘/d)

圖4為方向分布系數與雙向平均延誤的關系曲線。從圖4可知，2個方向的平均延誤隨方向分布系數增加而降低，這是因為方向系數越大則航道單向運行的連續性越強。對比不同航行規則的影響，β< 0.6時，兩種規則下的延誤情況基本相同；β=0.6～0.9時，采用管制規則能夠減少約9%～35%船舶延誤；β> 0.9時，此時兩個航向船流量比值已達到9:1，航道基本為單向運行，管制規則能夠發揮的作用很小。在運行實踐中，可根據船流量方向的分布合理組織交通，減小船舶延誤。

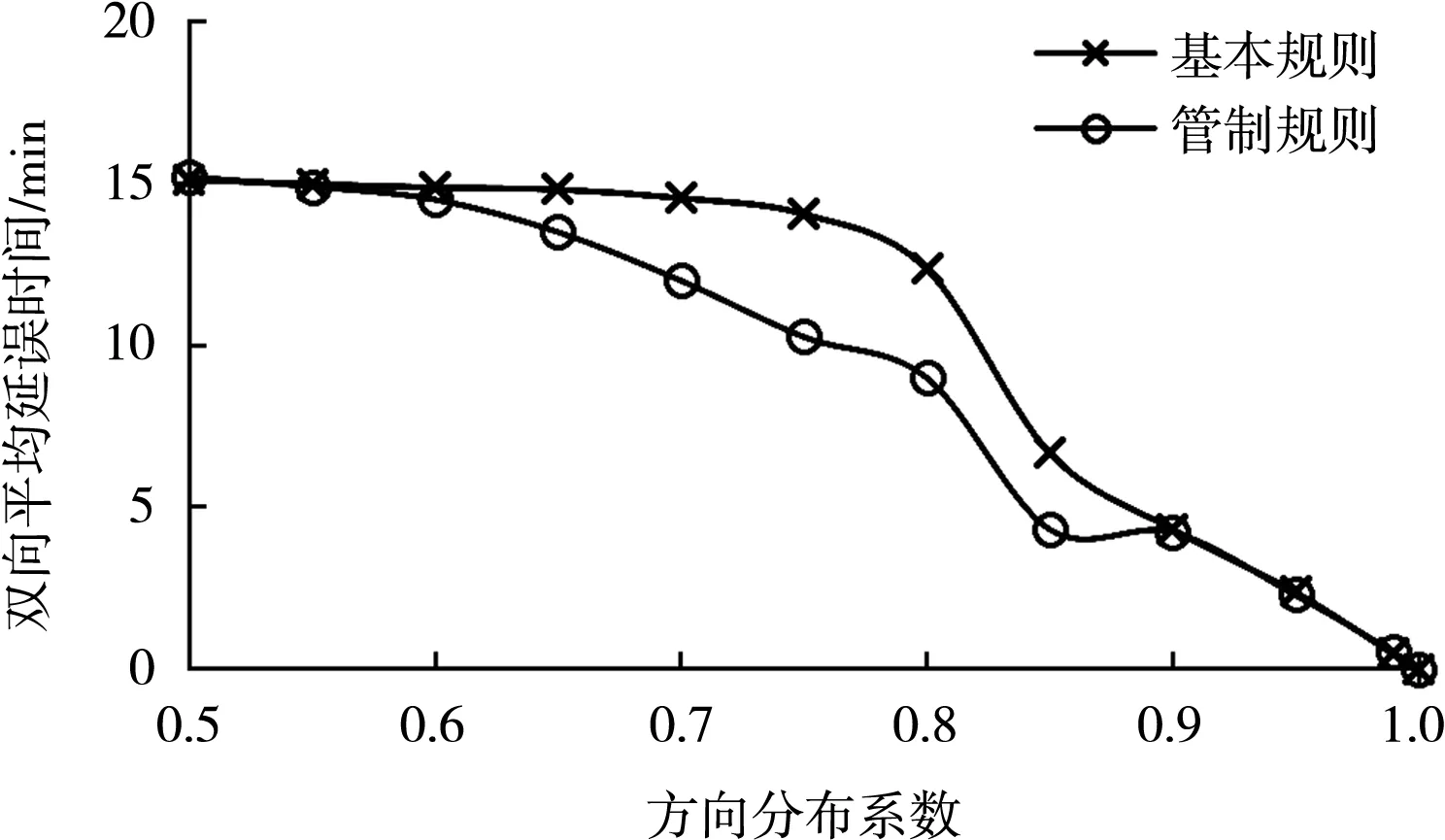
圖4 方向分布系數與雙向平均延誤的關系

2.3 通過能力與縮窄段長度的關系

考慮排隊系統的穩定性，當航段通過量不再隨排隊長度的增加而提升時，對應的通過量即為該條件下的最大通過能力[14]。假設2個航向船流量相同，船舶按基本規則，計算不同縮窄段長度下的航道通過能力，繪出平均排隊長度與單向通過能力的關系曲線(圖4)。從圖5 可知，大浦線航道局部縮窄段(L=280 m)單向最大通過能力約為361艘d，遠大于2015年實際單向日平均船流量38艘d，表明在現有條件下能夠滿足通航需求，采取單線通航是較為經濟可行的方案。另外，根據航道的設計條件(船舶平均噸位1 000 t，通航保證率98%，日工作系數0.75)[15]，得到單向最大通過能力為9 685萬ta，約為主航道設計單向最大通過能力(10 911萬ta)的89%。

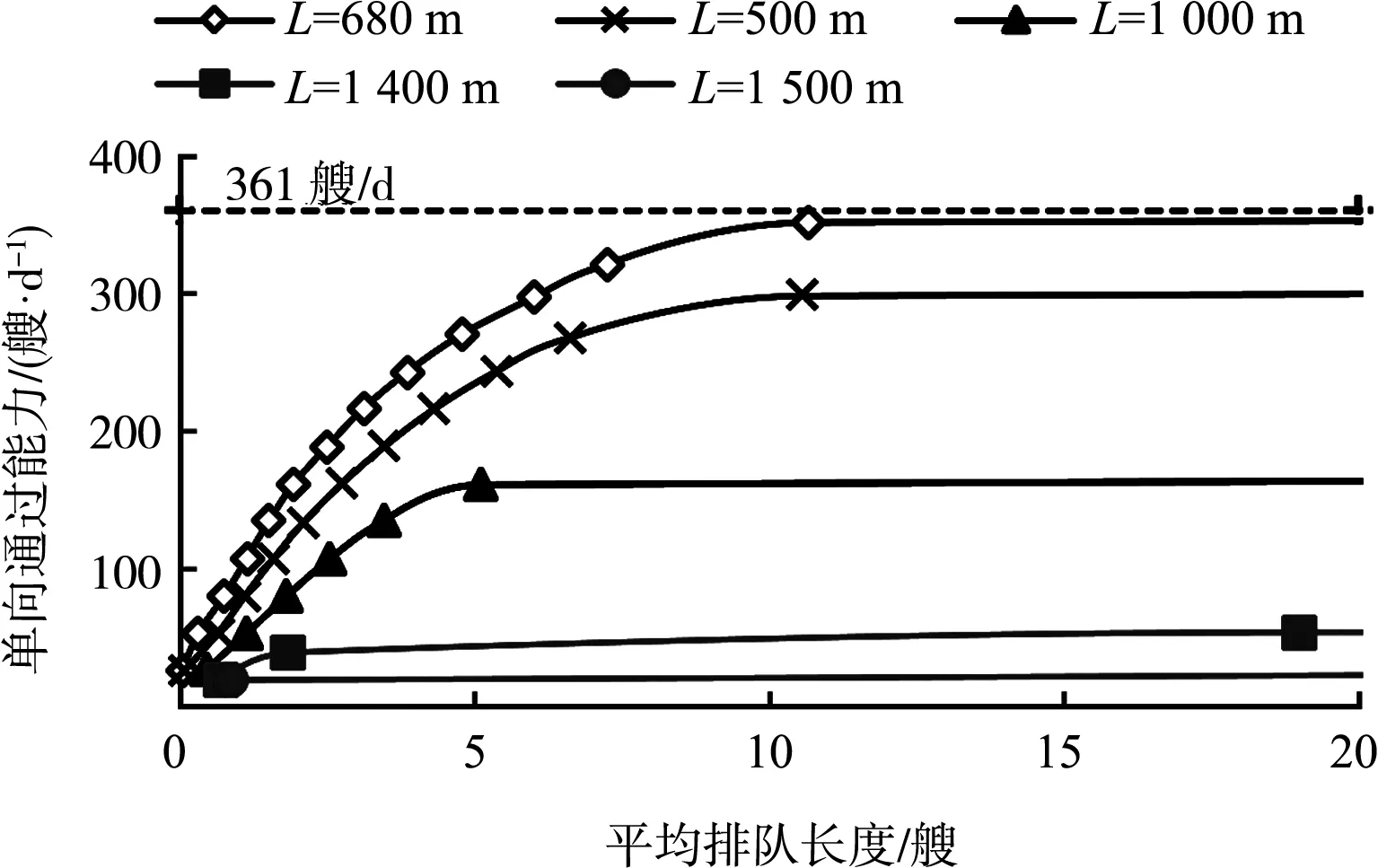
圖5 平均排隊長度與單向通過能力的關系

在圖5的基礎上，進一步分析局部縮窄段長度與單向最大通過能力的關系，如圖6所示。由圖6可知，航道最大通過能力隨縮窄段長度的增加而不斷降低。當L=1 500 m時，對應的航道單向最大通過能力已接近某一極小值(33艘d)，隨后的通過能力并不隨局部縮窄段長度的增加而顯著減小，表明當船流密度或需求小于該極小值時，局部縮窄段的長度仍可進一步增加。這為部分通航船流密度較低且受空間條件限制的航道不得已采用單線通航提供了理論基礎。

圖6 局部縮窄段長度與單向年最大通過能力的關系

3 結語

1)基于航道局部縮窄段的特征和航行規則，建立交通仿真模型重現船舶航行的動態過程，能夠得到各項交通運行指標，定量預測航道通過能力，為航道規劃、設計與運營提供依據。

2)仿真結果表明，船流量大小和方向分布影響航道的交通運行狀態，方向分布系數β在0.6～0.9時，船舶集中通過有助于提高縮窄航段的通航效率，但會增加部分船舶的延誤。實踐中可根據到船情況，合理安排交通組織策略，協調船舶延誤和航段通航效率的關系。

3)仿真結果表明，縮窄航段的通過能力隨縮窄段的長度增加而減小，但當縮窄段長度增加到一定值后，航段的通過能力接近某一極小值。這為部分通航船流密度較低且受空間條件限制的航道采用單線通航提供了理論基礎。實踐中可根據航運需求，經濟、合理地安排航道整治方案。