基于混合人工勢場與蟻群算法的多飛行器沖突解脫方法*

管祥民 呂人力

(中國民航管理干部學院民航通用航空運行重點實驗室1) 北京 100102)(浙江建德通用航空研究院2) 杭州 310025)

0 引 言

人工勢場法在過去的20年間被廣泛的運用于運動機器人導航，實時規避障礙物，其在線的避障有很強的魯棒性，能夠處理比較復雜的環境.然而，其運用在飛行器沖突探測和解脫方面并沒有像機器人領域那么廣泛，除了機器人領域比較活躍以外，另外一個可能的原因是飛行器運動模型的限制.Tomlin等[1]將該方法沿用到沖突解脫領域，基本思路是建立基于勢力和渦流場(potential and vortex field methods)的運動規劃來產生沖突解脫的機動策略.力場法用相對比較簡單的力學方程，得到連續的沖突解脫路徑，但是其隱含的一個假設是飛行器能夠隨著不斷變化的力場進行連續的機動，或者飛行器的速度能夠在很大的范圍內變化，這和實際都是不符的.在轉彎角度有限制的情況下，算法產生極端“不實際”的解.

在基于進化算法的沖突解脫方面，Durand等[2]利用遺產算法建立了一個簡單的神經網絡，在解決兩機間的短期沖突能得到滿意的結果，可靠性和計算效率都比較高.解決沖突解脫的神經網絡可以通過遺傳算法進行訓練，不必知道初始最優解就可以得到適合的解脫路徑，將遺傳算法所得到的每一代結果代入神經網絡中，使得神經網絡的適應性得到提高.但是神經網絡法對多于兩架飛行器的沖突拓展十分困難.三機沖突比兩機沖突的學習適應性差，而且在三機以上沖突的情景中，神經網絡的規模呈指數級增加學習非常困難.文獻[3]中基于遺傳算法的沖突探測和解脫方法已經用于NASA Langley 研究中心的試驗項目Airborne User Traffic Intent Information(AUTRII)，應用于飛行的爬升、轉彎、下降階段未來6～25 min內沖突預測和解脫.不僅可以用于飛行器之間沖突解脫，也可以用于危險區域(如SUA和雷雨云)的規避.由于在設計適應度函數的時候靈活性比較大，可以滿足操作人員不同情況下的不同優化目標(最小時間延誤，或者是最小航向角的改變等等)[4-9].

基于人工勢場法等分布式方法,計算速度快，但可能會產生不切實際的解；基于進化算法等集中式方法可靠性高，但是計算量大，響應速度較慢，實時性差.本文結合人工勢場法與蟻群算法的優點提出改進混合沖突解脫方法，利用人工勢場法迅速得到近似可行的沖突解脫路徑，然后將方案調整、編碼得到“權威螞蟻”，由“權威螞蟻”衍生“權威蟻群”，利用“權威蟻群”始化信息素矩陣，基于蟻群算法，求得含有飛行規劃約束的解脫方案.并通過與傳統的人工勢場法與蟻群算法進行比較，驗證了改進算法在時效性和可行性上的優點.

1 混合人工勢場與蟻群算法

1.1 利用人工勢場法得到初始路徑

將沖突解脫問題進行巧妙的轉換，將目的地看作正電荷，所有飛機看作負電荷.這樣，異種電荷互相吸引的作用保證了每架飛機會飛往目的地，而同種電荷互相排斥的作用則保證了不會發生飛行沖突.通過合理構造正負電荷的電場，將其化為物理學問題，對各飛機受力分析，確定運動軌跡,見圖1.具體來說，假設有N架飛機，第i架飛機的位置為xi=(xi,yi).

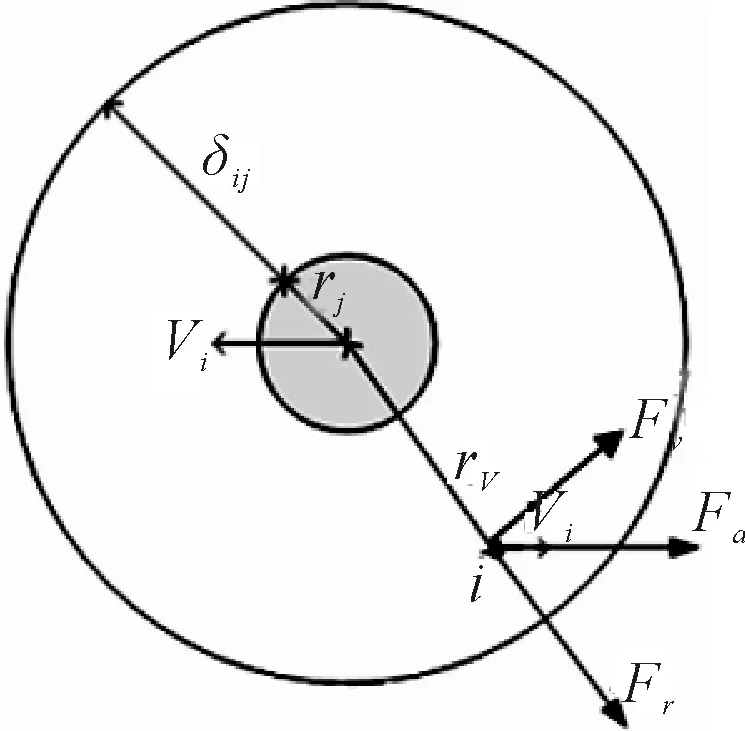
圖1 受力分析

為了確保飛機能飛往目的地，目的地xdi=(xdi,ydi)會激發引力場勢場函數

(1)

目標點產生的引力

Fa(xi,xdi)=-Ua(xi,xdi)=-(xi-xdi)

(2)

為了避免和飛機j碰撞，飛機j會激發斥力場Ur(xi,xj),

(3)

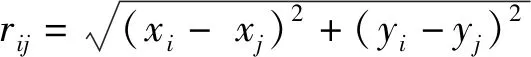
式(3)為了保證遇到沖突時飛機都能向同一方向轉彎，引入與斥力場相切的渦旋場

(4)

將上述三個力場疊加，就可以得到多機情況下動態的路勁規劃方程：

kviFv(xi,xj))j=1，2，…，m，i≠j

(5)

斥力和渦旋力在[0,1]間取值，其大小可控制解脫路徑的弧度.將牽引力歸一化是為了使其和斥力、渦旋力的量級一致，這樣其大小就和飛機到目的地的距離無關，僅指示去往目的地的方向.斥力系數kri、渦旋系數kvi用來控制斥力、渦旋力影響速度的權重.

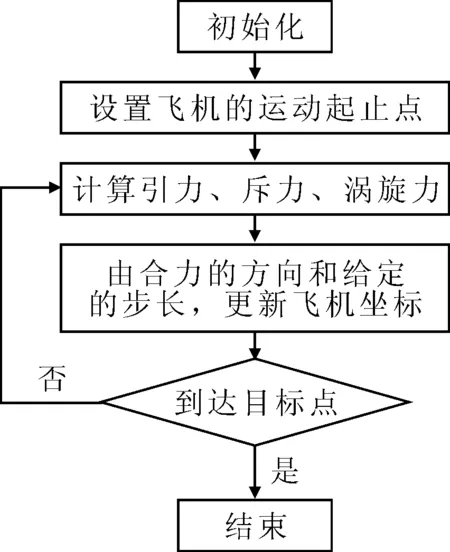
圖2 人工勢場流程圖

1.2 “權威”螞蟻

勢場法每步的航向由目的地的引力和其他飛機的斥力共同決定，這就使得其航向偏轉在實數范圍內取值；按照航向偏轉只能取0°，±30°這三個離散的值.為了使人工勢場的結果能順利編碼，有必要將人工勢場的規劃結果做適當的近似.事實上，只要確定了每架飛機解脫過程中每步的航向，解脫方案就唯一確定.如果飛機沿著之前的航向飛行與勢場法要求的航向的偏差在容許誤差(15°)內，則沿原航向飛行，反之做相應的調整.

近似后的航跡就可以按照之前約定的方式順利編碼，就可以得到“權威螞蟻”的覓食路徑.

1.3 “權威蟻群”

為了避免單次近似所帶來的偶然誤差，盡可能的全面地表征勢場法得到的解脫軌跡，借鑒遺傳算法基因變異的相關理論，由這只“權威螞蟻”衍生“權威蟻群”.

假設“權威螞蟻”的路徑X=(x1,x2,…，xN*K)，xi∈{-1 1 0}，X的N×K個分量亦可看作該路徑的基因.進行變異操作，隨機選取其中若干分量，對每個分量，令其等概地向另外兩種可取值變異.然后，對變異后產生的新個體進行安全性檢驗: 將變異后的x解碼，檢驗其對應的解脫方案是否滿足安全性要求.如果滿足安全性要求(即沒有飛行沖突)，就認為成功衍生了另一只“權威螞蟻”.重復這樣的操作，可以得到“權威蟻群”.

1.4 初始化信息素矩陣

每一只“權威螞蟻”會根據解碼后對應解脫方案的延誤，在其路徑上適當分泌信息素，而使路徑上每一節點的信息素得到更新.更新方程為：τij(t+1)=(1-ρ)τij(t)+Q/S.

將“權威蟻群”的所有螞蟻按上述方程更新它們經過的節點的信息素，就完成了初始化信息素矩陣的工作.

1.5 蟻群算法

利用蟻群算法解決沖突解脫問題，兩個難點：①如何將沖突解脫方案映射為螞蟻覓食路徑，即編碼問題；②定義怎樣的路徑為找到食物，即優化目標問題.鑒于此，下面將分三個部分闡述利用蟻群算法求解沖突解脫問題的流程.

1.5.1編碼

為了在保證精度的情況下盡快獲得計算結果，算法設定仿真步長為10 km，即每10 km更新一次航路點，這樣，就可以將任意一架進入扇區的飛機的解脫過程離散化為K步.在每一步中，飛機保持一定的速度和航向，在進入每一步之前飛機的航向能做出調整，見圖3.

考慮到民用飛機在巡航階段正常飛行，一般沒有大角度轉彎或轉向飛行.做出如下假設：飛機在解脫過程中只能選擇三個飛行方向，即保持原有航向，左轉30°，右轉30°.這種假設除了簡化搜索空間，還可以減少飛行員的反應時間，使其更好地執行沖突解脫方案.

綜上，假設N架飛機在解脫過程中分為K步進行調整，將每步的調整方式用1(代表右轉30°)，-1(左轉30°)，0(保持原航向)編碼，則每一種解脫方案被編碼為一個N×K維的向量X=(x1,x2,…，xN*K)，xi∈{-1 1 0} (每k個分量對應一架飛機的解脫軌跡).

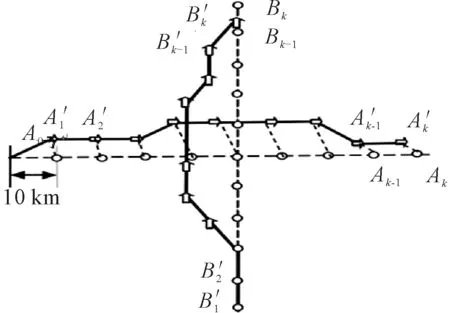
圖3 離散化的解脫航跡

假設螞蟻要穿越一個3×NK的迷宮，從第一列運動到最后一列覓食，每一列有三個節點供螞蟻選擇.這樣，螞蟻的每一條覓食路徑就對應上文所述的編碼向量，進而對應一個沖突解脫方案，至此我們完成了編碼的工作，見圖4.

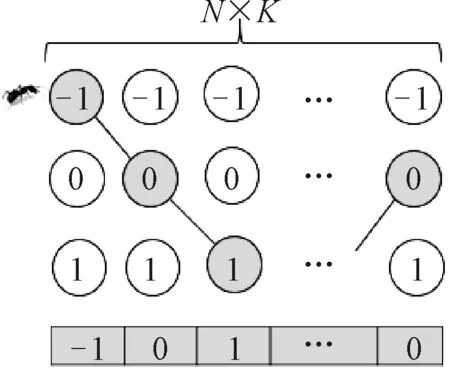
圖4 編碼機制

1.5.2優化目標

為了保障飛行安全，任意時刻、任意兩架飛機間的距離大約最小安全間距σ(20 km).對于離散化的沖突解脫過程，需要滿足的約束條件為：|A′i-B′i|>σ，i=1,2,…,k(|A′i-B′i|表示第i步A、B兩架飛機的直線距離).

那么，當螞蟻路徑所對應的解脫航跡滿足上述安全性的要求時，就可以認為該螞蟻找到了食物，從而會在該路徑上分泌一定量的信息素來引導后續螞蟻，否則，則認為該路徑為無效路徑，螞蟻不會分泌信息素.

滿足安全性的條件下，為了評價不同的解脫方案，定義飛機的延誤Si.這里，假定每架飛機解脫過程飛行的距離和預設的飛行距離保持不變.具體來說，假定按照飛行計劃，A飛機由A0飛往Ak是200 km的飛行距離，那么解脫方案也只規劃200 km的飛行軌跡.為了規避沖突，A必須在飛行過程中進行航向的調整，這樣飛行200 km后，A就不能到達Ak，而是落在了與其相近的A′k.將二者的距離定義為飛機在該種解脫方案下的延誤：Si=|A′k-Ak|.為了順利達到目的地，飛機要補償飛行Si，顯然，為了規避沖突而帶來的額外運營成本、航班延誤都和Si正相關，故而可以選擇它作為評價解脫方案的指標.

定義解脫方案的延誤S為所有飛機的延誤的和，即S=∑Ni=1Si.S越小說明解脫方案越優秀，映射到蟻群算法中，可以認為該方案所對應的螞蟻路徑找到了更多的食物，從而會在該路徑上分泌更多的信息素.

1.5.3迭代尋優

模擬螞蟻自組織過程、程式化地迭代尋優，如下幾個參數直接決定螞蟻路徑.

1) “迷宮”每個節點的信息素τijτij為第j列第i個節點的信息素.每當有成功覓食的螞蟻經過該節點時，螞蟻就會根據路徑譯碼后對應的解脫方案的延誤適當分泌信息素，而使該節點的信息素得到更新.更新方程為

τij(t+1)=(1-ρ)τij(t)+Q/S

(6)

式中：ρ為揮發系數，取值介于0到1，表征上一代螞蟻留下的信息素的揮發速度；S為前文定義的解脫方案的延誤.已分析過，S越小，解脫方案越優秀，故而要求螞蟻分泌的信息素越多，二者存在負相關的關系.本文取反比來近似.Q為增益系數.將螞蟻每次迭代分泌的信息素調整到合適的量級.

2) 螞蟻的轉移概率PijPij為螞蟻第j步選擇第i個節點的概率，設定螞蟻選擇每個節點的概率和該節點信息素的強度成正比，就有：Pij=τij/∑3i=1τij

經過“權威蟻群”初始化信息素后，第一代螞蟻選擇每一節點的概率和該節點信息素的強度成正比，即：Pij=τij/∑3i=1τij.由于“權威蟻群”根據人工勢場法得到的解脫方案調整而來，利用其初始化信息素后能引導大量螞蟻找到不發生沖突的安全路徑，這樣就避免了基本蟻群算法在初期沒有信息素的指引，完全隨機探測，得到大量無效路徑的問題.

如前文所述，處于無效路徑的螞蟻不會分泌信息素，只有確保飛行安全的前提下，螞蟻才會根據延誤量在各自路徑上適當分泌信息素，以此來引導后續螞蟻，進而形成信息素的正反饋來加快解的收斂.利用“權威蟻群”初始化信息素保證了蟻群初期就能迅速搜索到安全路徑，讓其快速進入“正反饋”過程，這無疑會極大加快算法的收斂速度.

2 實驗分析

2.1 場景描述

在經典對飛場景下，所有的飛飛行器均勻分布在同一個圓周上，該圓的半徑為100 n mile，每架飛行器將沿著一條直線飛行.顯然，如果沒有進行沖突解脫調控，沖突將發生在圓周的中心點上.雖然這種極端情況似乎不太可能在現實中發生，但它可以洞察在極端情況下，算法在復雜的飛行器沖突解脫場景中處理問題的性能和效率.經典對飛場景見圖5.

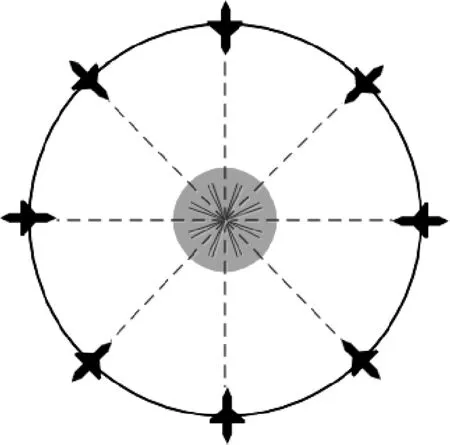
圖5 經典對飛場景示意圖

2.2 評價指標

實驗將采用四個主要指標來評估飛行器沖突解脫方案的質量即：沖突概率，計算時間，可行性，以及系統效率.

沖突概率是評價飛行器沖突解脫方案系統安全性的一個重要指標，為

(7)

式中：Cj為第j個飛行器的沖突數；n為飛行器的總數.

考慮到飛行器在高速飛行時需要實時解決飛行沖突，以確保飛行安全.有效縮短計算時間是不同的算法需要解決的重要問題.

引入參數算法的平均計算負荷，可表示為

(8)

式中：m為實驗重復次數；Tj為第j次實驗所需要的時間.

在某些飛行器沖突解脫方案中，有些方案的航向改變量可能太大，超出了飛行器機械性能可以實施的范圍，記為一次不可行點.

可行性可以表示為

F=∑ni=1fi

(9)

式中：fi為第i架飛行器在飛行器沖突解脫方案不可行點的數量；F為用來評估一個飛行器沖突解脫方案可行性的參數.

系統效率為

(10)

式中：Si為第i個飛行器延誤；Sdi為第i個飛行器的預設步長.顯然，當所有的飛行器沿預定的航跡飛行時，SE=1；當涉及的參與沖突飛行器的數量增加時，SE將會相應減少.

2.3 經典對飛場景下解脫方案對比

由于所有的飛行器都會在同一時間通過圓的中心，每架飛行器必須改變它的航跡，以避免沖突.

在經典對飛場景中，改進算法與其他方法的性能參數對比見表1.由表1可知，改進后的算法的優越性隨著飛行器數量的增長得到更好地體現.盡管改進后算法的性能參數并不是都是最好的，但他們與最好的性能差別并不是特別大.在實際情況下，改進算法的每一個解都是可行的，符合實際工程應用的要求，即獲得“不是最好的，但最有效的”解決方案.

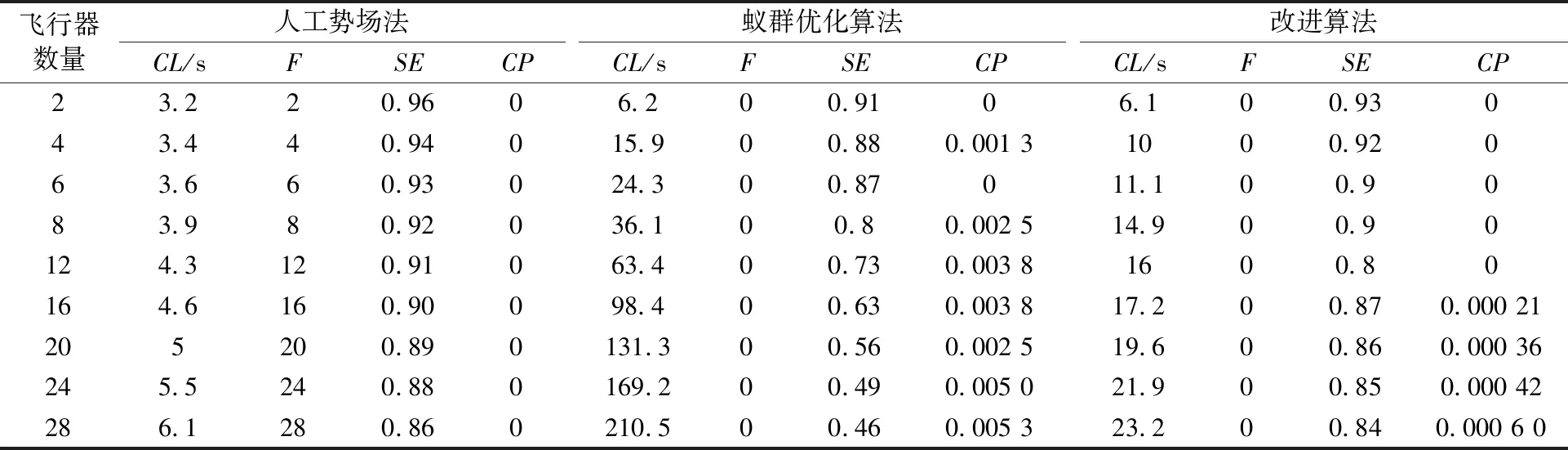
表1 經典場景下人工勢場法、蟻群算法的和改進算法性能參數對比

注：CL-計算時間；F-可行性；SE-系統效率；CP-沖突概率.

在經典對飛場景下，比較三種算法的計算時間、可行性、系統效率和沖突概率的對比圖見圖6.

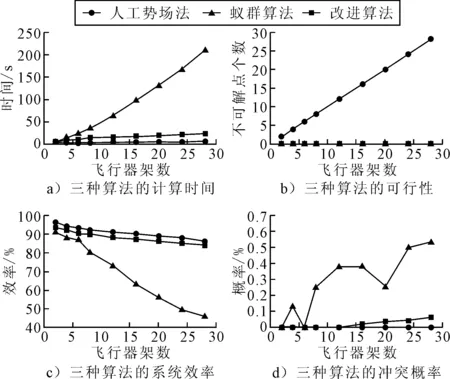
圖6 三種算法在經典對飛場景下的對比

由圖6a)可知，當飛行器架數超過12架后，蟻群優化算法的計算時間已經超過60 s，不符合沖突解脫實時性的要求.雖然人工勢場法的計算時間略小于改進算法，但兩者算法計算時間相差不大，都符合沖突解脫時的實時性需求.

由圖6b)可知，人工勢場法不符合可行性要求.在改進算法中，飛行器只能選擇三個飛行方向，即保持原來的方向不變，左轉30°或右轉30°.這個假設可以保證確改進算法得到的飛行器沖突解脫方案是可行的.此外，該假設不僅減少了搜索空間，也減少飛行員所需的反應時間，使飛行器沖突解脫方案的更容易實施.

由圖6c)可知，改進算法的系統效率明顯高于基本的蟻群優化算法，但略低于人工勢場法.由圖6d)可知，蟻群優化算法的沖突概率遠高于人工勢場法和改進算法.

人工勢場法在計算時間較短、系統效率和沖突的概率較低，但算法的可行性欠佳不能應用于實際場景.蟻群優化算法的性能也不理想.改進后的算法在所有四個指標(即計算時間、可行性、系統效率和沖突概率)上均符合實際場景的需求，并有著較好的速度與效率.

3 結束語

基于人工勢場法等分布式方法雖然計算速度快，但可能會產生不切實際的解；基于進化算法等集中式方法可靠性高，但是計算量大，響應速度較慢，實時性差.本文結合人工勢場法與蟻群算法的優點提出改進混合沖突解脫方法，利用人工勢場法迅速得到近似可行的沖突解脫路徑，將方案調整、編碼得到“權威螞蟻”，由“權威螞蟻”衍生“權威蟻群”，利用“權威蟻群”始化信息素矩陣，基于蟻群算法，求得含有飛行規劃約束的解脫方案.并通過與傳統的人工勢場法與蟻群算法進行比較，驗證了改進算法在時效性和可行性上的優點.