多車輛移動荷載和橋梁耦合振動的參數分析*

王 娟 張迎春 錢 江

(上海建橋學院商學院1) 上海 201306) (同濟大學土木工程防災國家重點實驗室2) 上海 20092)

0 引 言

車橋耦合振動的計算模型的差別主要在于車輛的簡化模型.車輛的簡化模型從簡單到復雜可分為四種類型：移動荷載、移動質量、單軸彈簧-阻尼-質量系統、多軸彈簧-阻尼-質量系統[1].Fryba[2]給出了不同車輛模型的控制方程及求解方法.肖新標等[3]對比了三種車輛模型作用下橋梁的動態響應.隨著研究不斷深入，車輛模型從一車模型發展到多車模型[4-5]，并且車橋耦合振動中的共振現象也引起了學者的關注.Yang等[6]以間距為列車長度的移動質量模擬列車荷載，并給出與車輛速度引起橋梁共振和消振的條件.李小珍等[7]建立了任意移動彈簧-阻尼-質量列模型作為多車輛荷載，分析了車速對橋梁響應的影響.李慧樂等[8]以移動荷載列為車模型給出簡支梁發生共振及兩類消振效應(單荷載和荷載間距)的車速計算公式，并指出消振與荷載間距有關.Yang等[9-10]進一步研究了車輛和橋梁共振的機理.Yang等[11]通過簡單的彈簧質量車模型和復雜的多體車模型分析驗證了一定跨度的連續橋梁引起列車共振的條件，以及車輛作用引起橋梁共振的條件.

目前，多車荷載的研究主要集中在車輛速度以及車輛間距和橋跨長度對橋梁動態響應的影響，車輛和橋梁的其他參數對系統響應的影響并沒有全面展開.而且過于簡單的荷載列模型不能真實的反應車橋耦合的振動效應，復雜車模型作為荷載激勵也不易在橋梁設計中推廣.鑒于此，文中選擇單軸彈簧-阻尼-質量系統為車輛模型進行多車荷載激勵的研究.橋梁簡化為簡支的歐拉梁，通過MATLAB編程計算，全面揭示橋梁和車輛參數變化的影響.主要內容如下：①對比現有文獻的計算結果，驗證一車和多車荷載的車橋耦合振動模型.②選擇跨長30 m橋梁在雙車或多車荷載作用下進行參數分析.選擇參數如下：車輛速度、車輛間距、車輛輪胎和懸架質量比、車-橋質量比、車輛剛度、車輛和橋梁阻尼特性,以及車輛軸數.

1 兩輛或多輛車運行下的車橋耦合振動計算模型

根據文獻[2]單軸彈簧-阻尼-系統建立一輛車的車橋耦合振動模型，推廣到多輛車激勵的控制方程.在實際工程中兩輛車或多輛車連續通過橋梁的情形非常普遍，對于橋梁的動態響應而言，多輛車激勵的響應并不等同于多個一個輛車激勵的響應疊加.兩輛車的車橋耦合振動計算模型見圖1.

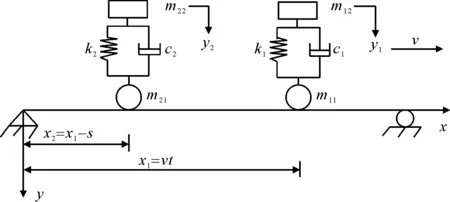
圖1 兩輛車與橋梁耦合振動的計算模型

相應的控制方程為

(1)

(2)

(3)

式中：yi為第i輛車懸架豎向位移；mi1和mi2分別為車輪輪胎和車輛懸架質量；t為車輛運行時間，從車輛接觸橋梁開始計算；y(x,t)為t時刻x處的橋梁豎向位移；E為橋梁的彈性模量；I為橋梁截面的慣性矩；μ為橋梁的線密度;c為橋梁的黏性阻尼系數，假定為Rayleigh阻尼；δ(x)為狄拉克函數；ki和ci分別為車輛剛度和阻尼系數；v為車輛運行速度；Pi=(mi1+mi2)g；s為車輛間距.文中忽略橋面粗糙度.

M輛車的車橋耦合振動的控制方程由M+1個方程組成，前M個方程是M輛車的控制方程，其中第M個、第M+1個方程是橋梁的控制方程為

(4)

(5)

y(x,t)可以采用模態位移改寫為

(6)

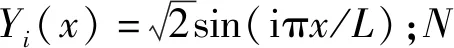
(7)

式中

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

{y}={y1,y2,…,yM}T

(18)

{T}={T1,T2,…,TN}T

(19)

P={∑M1PiY1i/L,∑M1PiY2i/L,…,∑M1PiYNi/L}T

(20)

式(7)～(20)采用Newmarkβ法進行編程求解.

2 車輛與橋梁耦合振動計算模型的驗證

模型驗證分為兩個方面：一車耦合振動模型和多車耦合振動模型的驗證.選擇Xiang等[12]算例驗證一車和多車計算模型.計算模型參數如下.μ=2.303×103kg/m，m11=0，m12=5 750 kg，k1=1.595×106N/m，c1=0，E=2.87 GPa，I=2.9 m4，橋梁的基頻為20.85 rad/s，橋梁的跨度為30 m，車輛速度為27.78 m/s.圖2為橋梁跨中豎向位移和懸架質量m11豎向位移的對比，由圖2可知，數值結果吻合良好，因而計算模型對于一輛車的荷載激勵是可靠的.

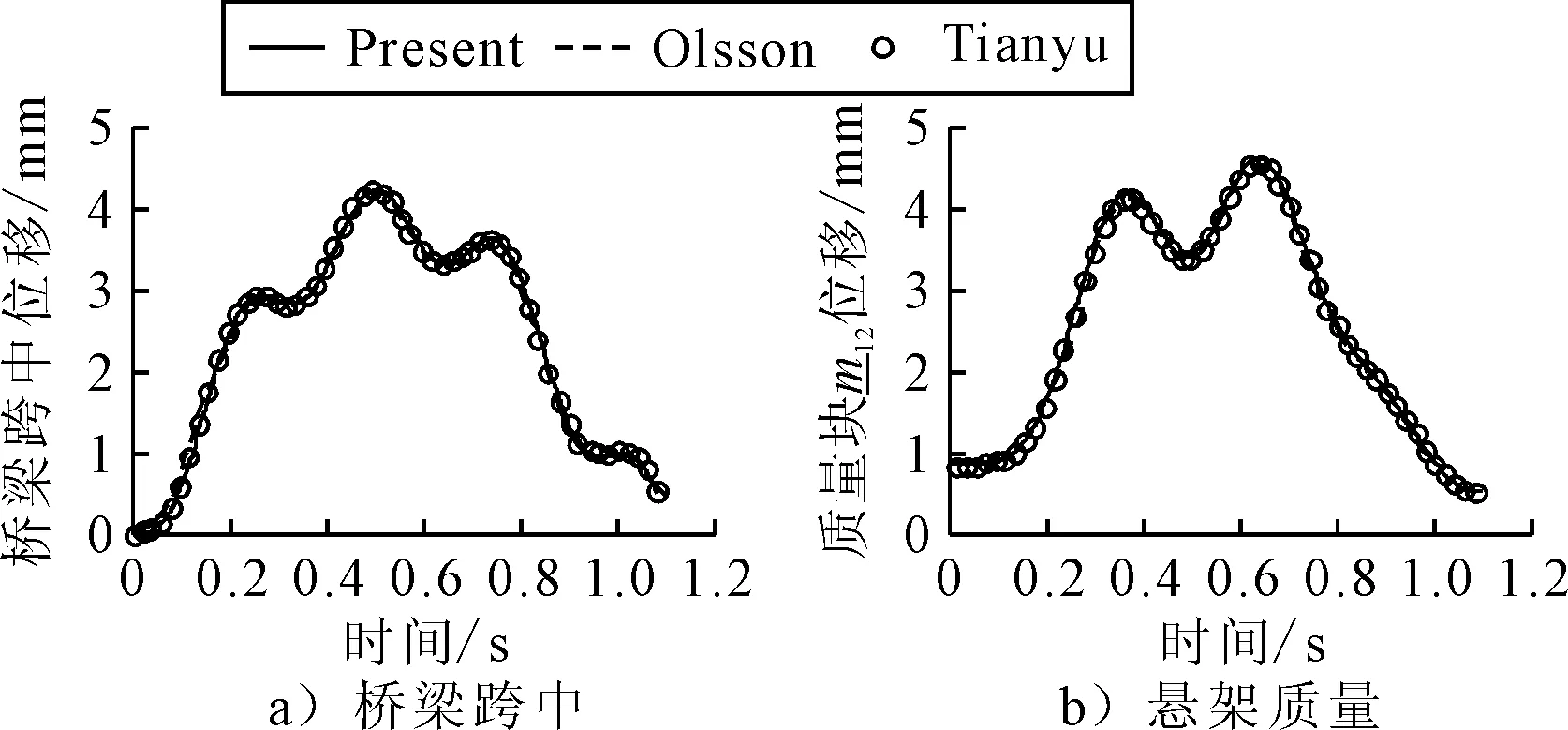
圖2 豎向位移時程

目前為止未見質量-彈簧-阻尼系統的多輛車算例的文獻，因而設定mi1,ki1,ci1為0，把多車輛模型退化為連續集中力與文獻[6]的算例進行對比驗證.算例中5車輛10個連續集中荷載以速度26和34 m/s通過橋，兩個速度分別對應消振和共振工況.模型數據為：μ=3.408 8×104kg/m，E=29.43 GPa，I=3.81 m4，橋梁的跨度為20 m，橋梁的基頻為44.75 rad/s，輪胎質量為22 000 kg.得出兩個速度工況的橋梁跨中位移和不同速度對應的最大位移見圖3～4.圖3結果表明，26 m/s的工況位移時程曲線的幅值和相位非常吻合.34 m/s的工況在曲線的局部峰值與文獻結果略有差異，但極值和相位均非常接近，文獻[6]的位移極值分別為0.32和-0.93 mm，文中的極值分別為0.33和-0.93 mm.圖4結果表明，計算結果非常接近，文中曲線最大值為3.69 mm，文獻[6]的最大值為3.66 mm，對應的速度無量綱參數S1相同.因而多車輛荷載的退化模型仍然是可靠的.通過一車輛模型和連續荷載列模型的算例驗證了本文計算模型的可靠性.

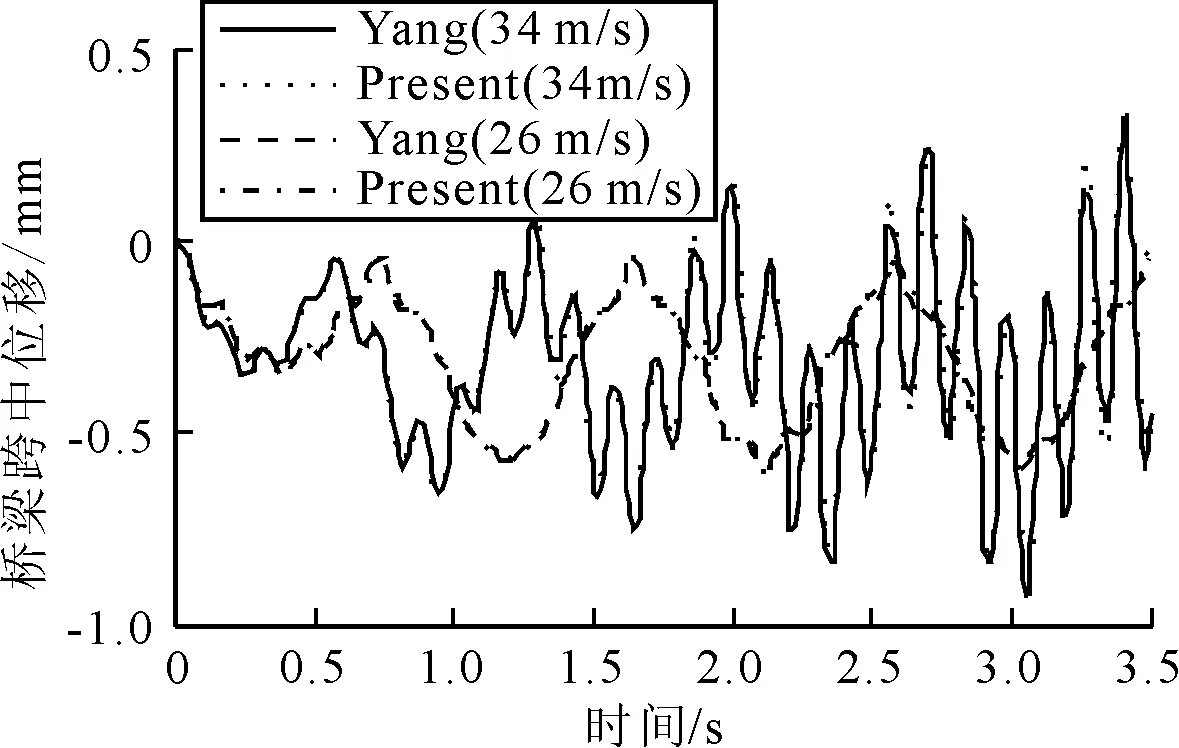
圖3 橋梁跨中時程響應

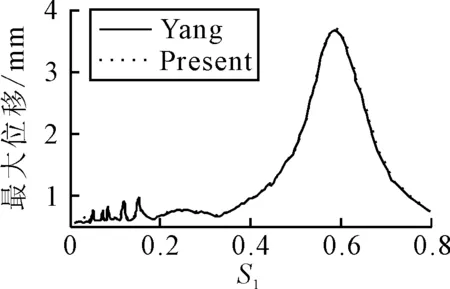
圖4 響應幅值與速度參數S1

3 兩輛車運行下的中等跨度橋梁的參數分析

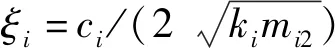
表1 車橋耦合振動計算模型的參數

引入動力放大系數DAL，研究橋梁的最大位移和特定參數之間的關系，計算公式為

DAL=δdyn/δsta

(21)

式中：δdyn為橋梁的最大動態響應；δsta為橋梁的最大靜態響應.一車模型作用下橋梁的最大靜態位移是車輛位于跨中引起的跨中靜態位移，相同間距的兩車或多車作用下橋梁最大靜態位移是車輛以跨中為中心，對稱分布于橋梁引起的跨中位移.

3.1 車輛速度的影響

多個車輛均采用相同模型，車輛速度從4 m/s增加到240 m/s，每次增加1 m/s.車輛間距均相等.車輛間距s=8 m的多個車輛運行下橋梁的動力放大系數與一車激勵的對比見圖5.由圖5可知，不同數量車輛的動力放大系數均有隨速度增加而增長的趨勢，最大峰值有降低的趨勢，與最大峰值和局部峰值相應的速度有增大的趨勢.在特定的速度區間(比如80～150 m/s)，速度不變的情況下，動力放大系數隨車輛數量降低，說明車輛的增加導致最大動態位移增長的速度小于最大靜態位移增長速度.對于橋梁工程師而言，需考慮多車輛運行的動力放大系數與一車的差異.

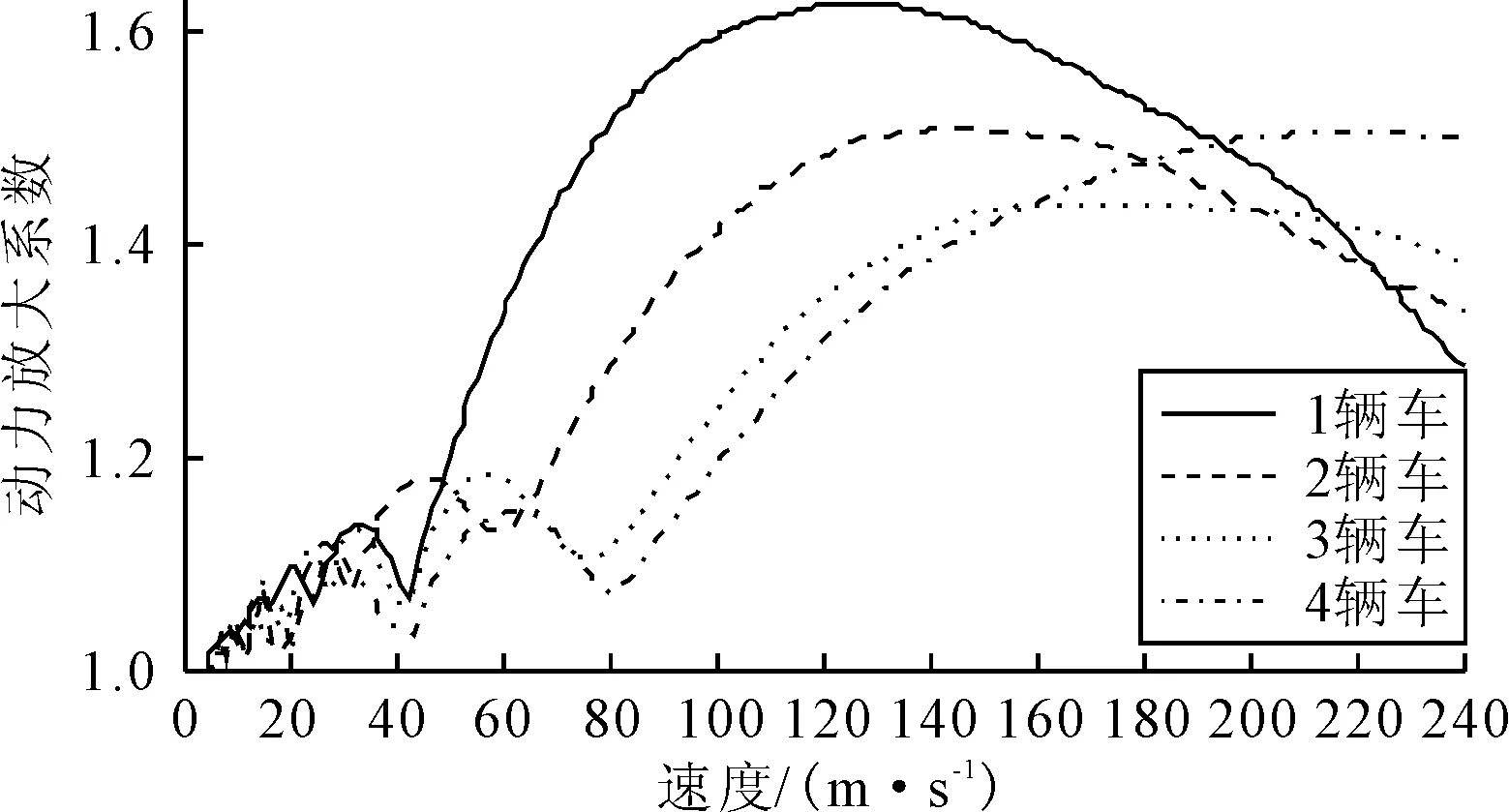
圖5 橋梁動力放大系數與速度(s=8 m)

文獻[6]給出了連續荷載列引起橋梁共振的速度公式為

v=sω1/2iπ (i=1,2,…)

(22)

式中：s為車輛間距；ω1為橋梁第一自然圓頻率，此公式適用于橋梁跨度不超過車輛間距的2倍，即s≥L/2.圖6為間距s=26 m的3～6輛車作用下的橋梁動力放大系數的對比.由圖6可知，不同數量車輛的動力放大系數曲線相位幾乎一致，只在接近局部峰值的范圍內幅值有差異.這是因為隨著車輛的增多延長了橋梁振動的時程，橋梁共振位移隨時間而增長，導致峰值的增加.表2為2～7 輛車連續通過引起的位移峰值對應的速度和動力放大系數.由表2可知，隨著車輛增加，局部峰值對應的速度逐漸接近文獻[6]的公式得出的共振速度，直到車輛增加到7輛，峰值對應的速度不再變化.實際上共振速度不僅限于式(22)給出的速度，在接近局部峰值速度的范圍內同樣具有共振效應.圖7為3輛車間距s=26 m在速度83，93，103 m/s的橋梁跨中位移時程曲線，除了峰值對應的速度93 m/s之外，83和103 m/s的速度工況同樣顯示出位移隨時間增長的共振效應.對于動力放大系數的曲線波段而言，從離開波谷速度63 m/s，從64 m/s開始就出現共振效應，到波峰對應的93 m/s共振效應最大，直到111 m/s之后共振效應不再明顯.因而峰值附近的速度工況產生的位移放大效應同樣值得橋梁設計師注意.

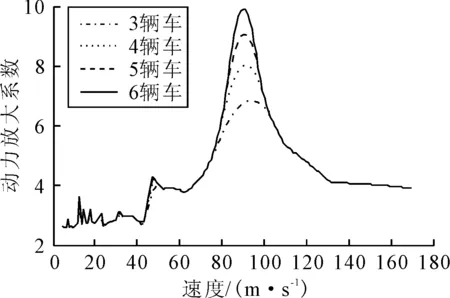
圖6 橋梁動力放大系數與速度(s=26 m)

3.2 車輛間距的影響

觀察恒定速度下車輛間距s變化影響橋梁動態響應的規律.選擇兩車模型進行研究，車輛間距0.5～29.5，每次增加0.5 m，選擇三個速度工況進行對比，分別為20，60，100 m/s.由于車輛間距29.5 m工況下橋梁最大靜態位移為0.19 mm，得出的動力放大系數遠遠大于間距較小的工況，因而選擇跨中最大動態位移進行觀察，計算結果見圖8.由圖8可知，橋梁位移響應并未呈現單調變化趨勢.對于20 m/s(72 km/h)的工況，當間距大于19 m(s/L>0.63)時跨中最大位移明顯降低；對于60 m/s(216 km/h)的工況，當間距在19～24 m(s/L在0.63～0.8)時跨中最大位移明顯降低；對于100 m/s(360 km/h)的工況，當間距在16～22 m(s/L在0.53～0.73)時跨中位移明顯降低.不同速度工況表現出在間距和橋跨比為0.6左右的位移較小.因而可以利用這個特點，選擇適當的橋梁跨度或車輛間距來設計橋梁或交通.

表2 不同數量車輛的共振速度和動力放大系數DAL(s=26 m)

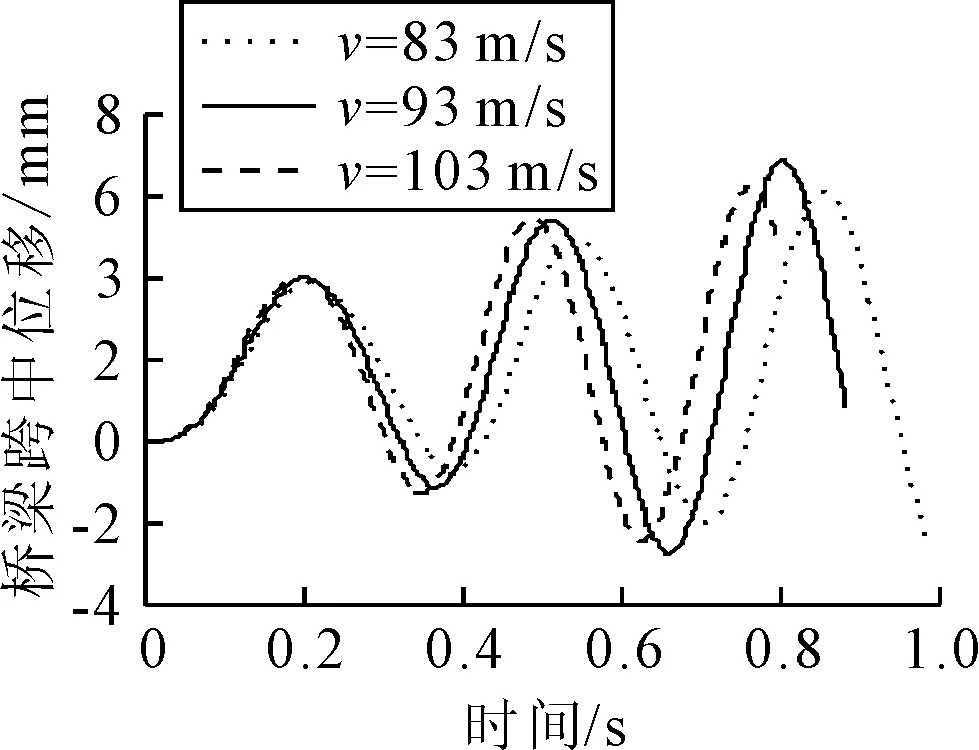
圖7 3車模型的橋梁跨中位移時程(s=26 m)

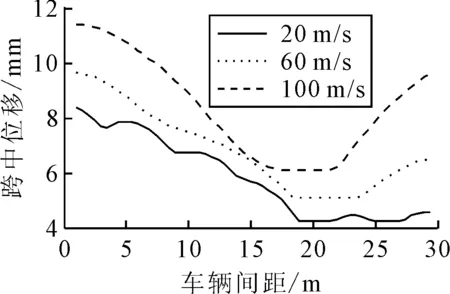
圖8 車輛間距變化對橋梁位移響應的影響

車輛間距和速度的變化對橋梁動態響應的影響可以繪制成云圖.圖9分別顯示了2～4輛車作用下橋梁的跨中最大動態位移的變化規律.可以觀察到特定間距下速度變化對跨中位移的影響，也可以觀察特定速度下車輛間距的變化對跨中位移的影響.這3張圖跨中位移的變化規律具有相似的變化趨勢，例如，3張圖均具有左上角跨中位移較小的特點，說明當速度小于40 m/s，車輛間距大于15 m(s/L>0.5)，橋梁跨中位移較小.云圖顯示速度越大、間距越小橋梁響應越大，但是當速度在90～110 m/s，車輛間距接近橋跨，盡管靜態位移較小，造成的動態位移仍然很大.

圖9 2～4輛車通行時橋梁最大跨中位移云圖

3.3 車輛質量變化的影響(mi1/mi2)

車輛質量的變化從兩個方面考察，一個是車輛輪胎和懸架質量比(mi1/mi2)的變化，另一個是車輛總質量與橋梁質量比(mi2/(μL))的變化.保持mi2不變，增大mi1的質量，mi1/mi2的變化范圍在0%～15%.動力放大系數的變化與速度有關，圖10為速度為20，60，100 m/s的兩車模型、車輛間距s=10 m的動力放大系數，三條曲線均呈現單調變化趨勢，其中20和60 m/s的工況動力放大系數隨質量比的增加呈減小的趨勢，而100 m/s的工況正相反，呈增加的趨勢.橋梁的動態和靜態響應均隨車輛質量的增加而增加，但不同速度工況動態和靜態響應的增長速度不同，導致動力放大系數變化趨勢有差異.變化幅度比較小，因而懸架質量不變的情況下，車輛輪胎質量的變化對橋梁動力放大系數的影響不大.

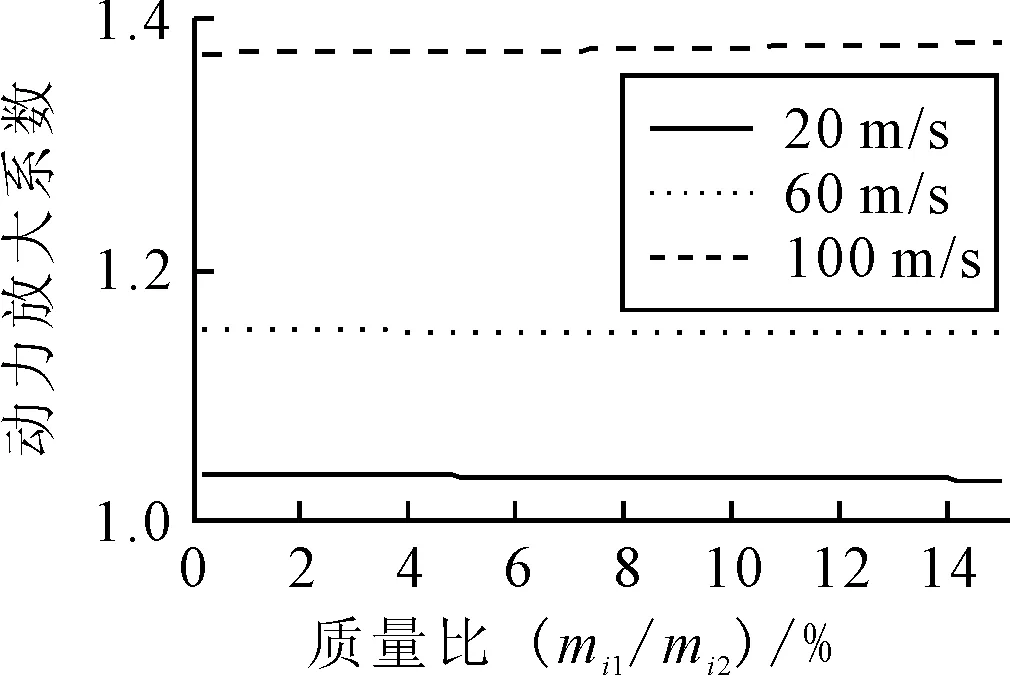
圖10 動力放大系數與車輛輪胎和懸架質量比(s=10 m)

保持mi1不變，增大mi2的質量，mi2/(μL)的變化范圍在0.2%～15%，即2輛車總質量與橋梁的質量比的范圍在0.4%～30%.得出的動力放大系數見圖11，由圖1可知，三個速度工況對應的動力放大系數變化規律均不同，沒有呈現單調的變化趨勢.20 m/s的工況動力放大系數在質量比為8.4%時達到最小值1.01，質量比為30%時達到最大值1.09.60 m/s的工況動力放大系數在質量比為12%時達到最大值1.15.100 m/s的工況動力放大系數在質量比為1.6%時達到最大值1.52，在質量比為30%時達到最小值1.33.不論單獨增加輪胎質量還是懸架質量，橋梁的跨中動態位移均呈現單調增加的形式，但動力放大系數與速度有關，而且車輛懸架質量的變化比輪胎質量的變化對動力放大系數影響更大.

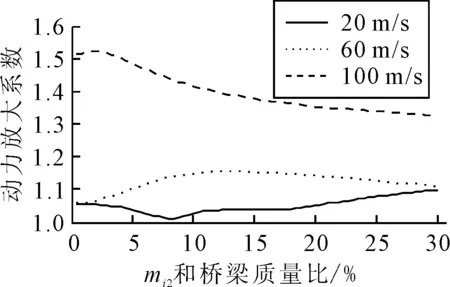
圖11 動力放大系數與車輛總質量和橋梁質量比(s=10 m)

3.4 車輛彈簧剛度變化的影響

車輛彈簧剛度ki的變化步長為50 kN/m，變化范圍為800～2 400 kN/m，這兩個限值是文獻[12]算例模型剛度的50%和150%.圖12為兩車模型、車輛間距s=10 m的速度和車輛剛度與動力放大系數的關系云圖.由圖12可知，同樣的速度，動力放大系數可能隨剛度增加也可能減小，或者呈現非單調的曲線變化趨勢.例如20和100 m/s的工況動力放大系數隨剛度的增加而減小，而60 m/s的工況呈增加的趨勢.20 m/s的速度工況動力放大系數從1.08降低到1.02，60 m/s的速度工況從1.06增漲到1.19，100 m/s的速度工況從1.41降低到1.36.盡管車輛剛度的變化對橋梁動態響應的影響與速度有關，但變化幅度并不顯著.

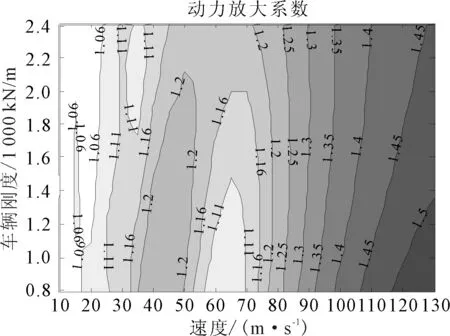
圖12 動力放大系數與車輛剛度和速度的變化云圖

3.5 車輛阻尼的影響

車輛阻尼從0 N·s/m增加到19.1 kN·s/m，對應阻尼比范圍0%～10%，增加步長為200 N·s/m.圖13為速度為20，60，100 m/s的兩車模型車輛間距s=10 m的動力放大系數，三條曲線均呈現單調變化趨勢，其中20和60 m/s的工況動力放大系數隨剛度的增加而減小，而100 m/s的工況正相反，呈增加的趨勢.說明車輛阻尼的增加并不必然導致橋梁響應降低.速度大于65 m/s的動力放大系數開始呈現隨阻尼增加而增加的趨勢，速度大于150 m/s的動力放大系數開始呈現凹曲線形式.盡管不同速度的動力放大系數曲線變化趨勢不同，變化幅度均不顯著.20 m/s的速度工況動力放大系數從1.03降低到1.02，60 m/s的速度工況動力放大系數從1.15降低到1.13，100 m/s的速度工況動力放大系數從1.37增漲到1.39.因而動力放大系數對車輛阻尼的敏感性較低.

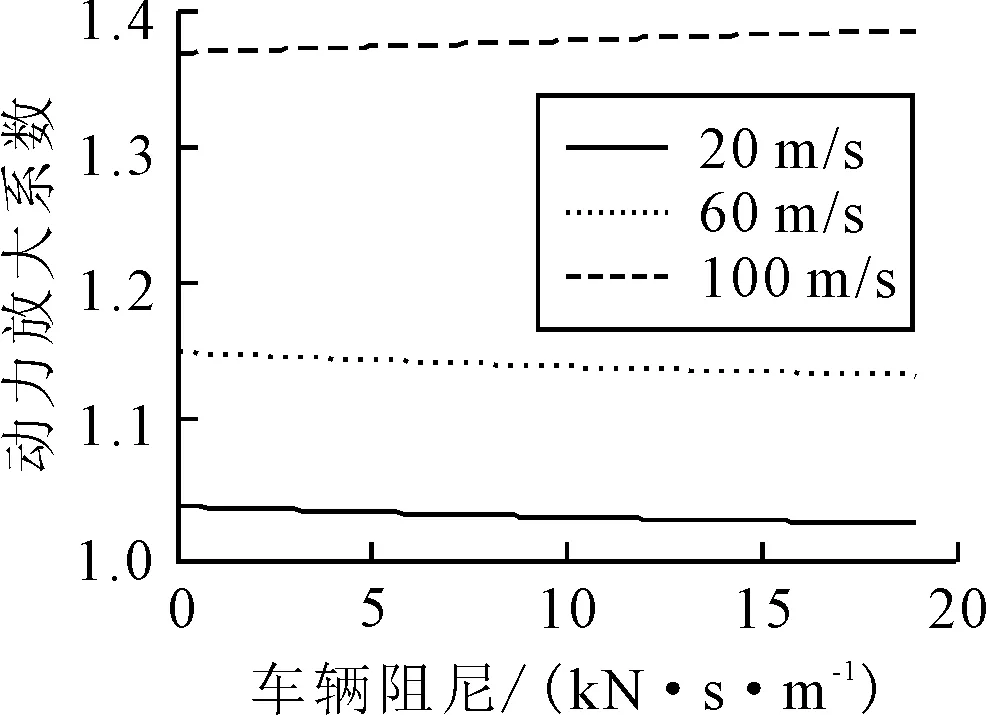
圖13 動力放大系數與車輛阻尼

3.6 橋梁阻尼的影響

橋梁阻尼比從0增加到10%，圖14為速度為20，60，100 m/s的兩車模型在間距s=10 m的動力放大系數與阻尼比的關系，20 m/s和100 m/s的工況動力放大系數隨阻尼比的增加而減小，20 m/s的速度工況動力放大系數從1.04下降到1.02，100 m/s的速度工況動力放大系數從1.37下降到1.31.而60 m/s的動力放大系數保持在1.15.圖15為不同阻尼比的動力放大系數與速度關系，事實上在61～72 m/s之間動力放大系數隨阻尼比的增加而增漲，這個區間也在消振速度區間，其他速度工況動力放大系數均隨阻尼比的增加而減小.圖16為65 m/s的工況在不同阻尼比下的跨中位移時程，由圖16可知，在阻尼為0，0.025，0.05對應的最大動態位移分別為7.28，7.33和7.36 mm，盡管位移隨阻尼比增大，但差異非常小.橋梁阻尼比的增大在某些消振速度工況不能起到減小振幅的現象在文獻[6]中也同樣出現，只不過作者并沒有解釋.粘滯阻尼對于減小共振峰值的作用非常明顯.

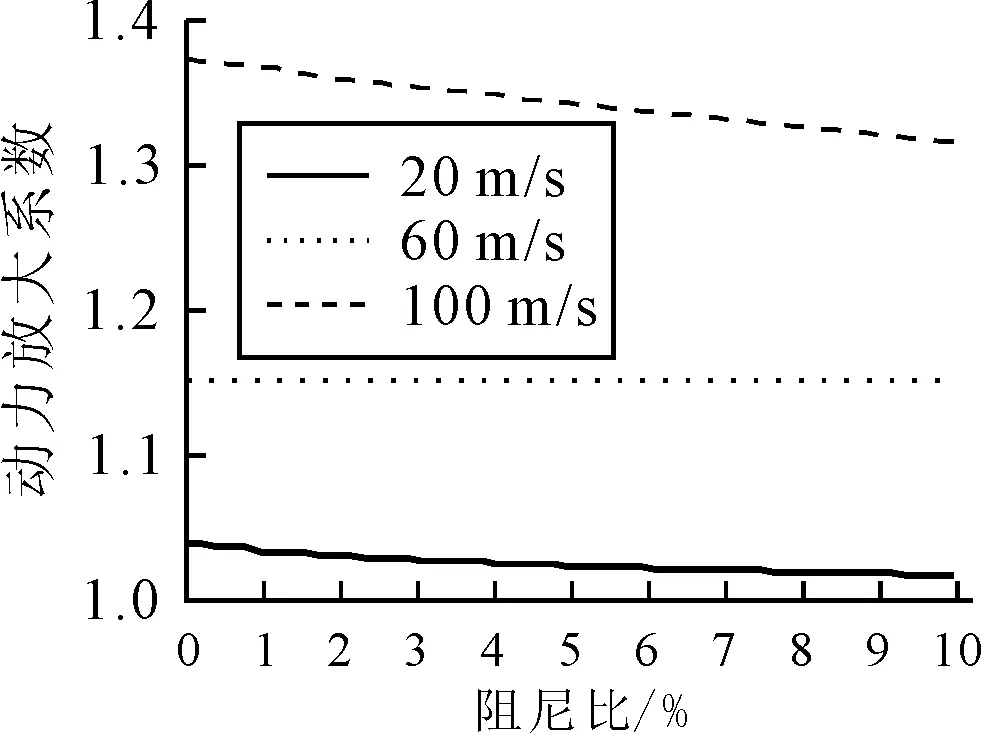
圖14 動力放大系數與阻尼比(s=10 m)

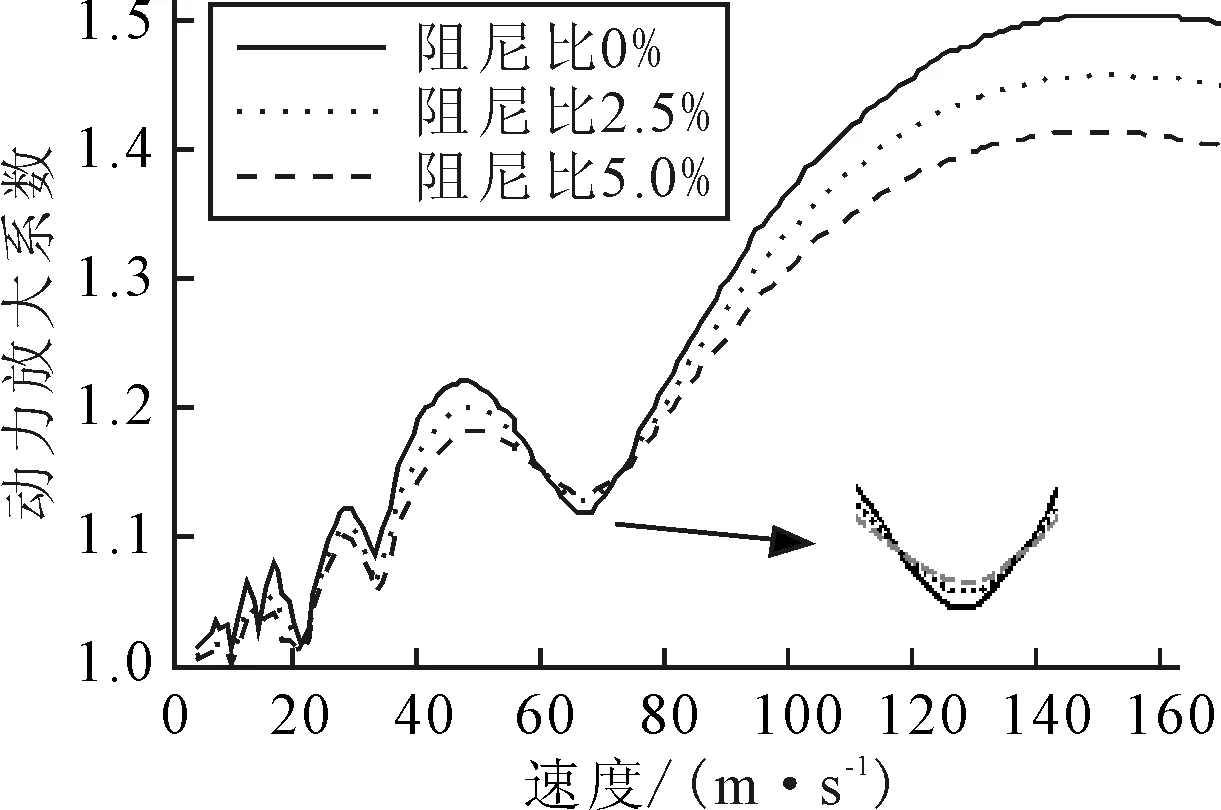
圖15 不同阻尼比的動力放大系數與速度關系

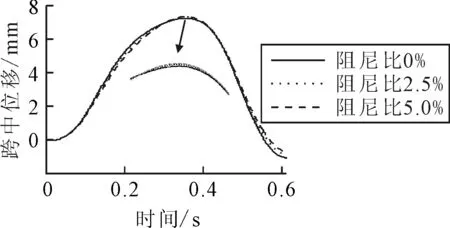
圖16 不同阻尼比的跨中位移-時程(v=65 m/s)

3.7 單軸車輛與雙軸車輛的比較

前面的計算結果均采用單軸車輛模型，采用雙軸或多軸車輛模型更接近實際工程.本節把單軸車輛的質量和剛度減半，使雙軸車輛的質量和剛度與單軸車輛相等.采用軸距2 m，車輛間距為s=26 m，與同樣間距的單軸車輛比較.圖17為4輛車單軸和雙軸模型的動力放大系數(7輛車的對比曲線與4輛車的曲線有相似的變化趨勢).由圖17可知，雙軸車輛與單軸車輛的動力放大系數在25 m/s以上的速度工況比較吻合，捕捉到的峰值點對應的速度也一致，11～19 m/s動力響應差異較大，4車模型單軸響應與雙軸響應最大差異33%，7車模型最大差異30%.因而對于城市交通限速20 m/s以下的橋梁采用雙軸車輛計算更加合理.

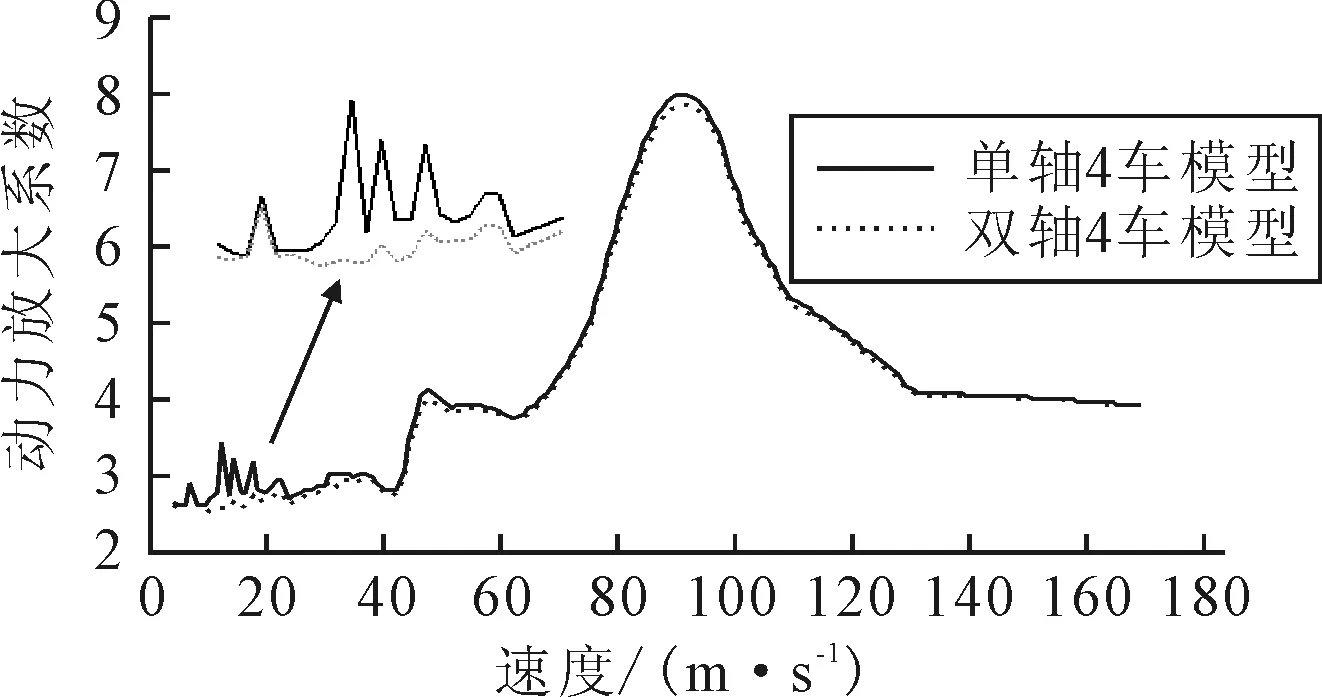
圖17 單軸和雙軸4輛車的動力放大系數(s=26 m)

4 結 論

1) 車輛速度對橋梁的動態響應影響較大，一輛車或連續車輛的移動荷載都會引起橋梁的共振效應，除了響應峰值相應的共振速度，也需要注意共振速度附近的位移放大效應.

2) 車輛間距的變化對橋梁動態響應也很顯著.由于間距接近橋跨長度靜態位移很小，造成動力放大系數很大，橋梁設計不僅需要參考動力放大系數，同時也想需要參照動態響應.車輛間距小于1/2橋跨時橋梁的動態響應隨間距增加而減小，在間距與橋跨比值0.6附近響應最小，這個特點可以作為橋梁或交通設計的參考.

3) 增加車輛的輪胎質量和懸架質量都會引起橋梁動態響應的增大，但動力放大系數的變化與速度有關，有些速度工況下動力放大系數呈下降趨勢，總體來說差異不大.車輛懸架質量的變化比輪胎質量的變化對動力放大系數影響更大.

4) 盡管車輛剛度的增加導致橋梁的動態響應因速度而不同，可能增加也可能降低，或呈現非單調的曲線變化規律，但變化幅度并不顯著.

5) 車輛的阻尼對橋梁響應的敏感性較低，但是橋梁的阻尼具有明顯的降低共振振幅的作用.

6) 雙軸和單軸的簡化車輛模型的分析表明：雙軸車輛模型對低速(11～19 m/s)的工況影響更大，其他速度工況與單軸車輛模型差異較小.

總之，橋梁和車輛的參數中車輛速度和車間距與橋跨比值對橋梁動態響應具有顯著影響，車輛總質量和剛度的變化對橋梁響應的影響隨速度而不同，可以利用參數變化的規律設計橋梁和交通.