解析數學建模在高中數學解題中的應用
曹彩霞
(江蘇省海門市四甲中學 226100)
數學模型是對實際問題的數學化概括與濃縮,是高中數學學習的重要內容之一.在當前大力提倡核心素養培養教育背景下,數學建模能力被納入核心素養的重要構成部分,因此授課中應提高認識,注重數學建模的應用講解,提高學生的數學建模意識以及能力,為核心素養的提升奠定堅實基礎.
一、認真審題,構建函數模型
學生對函數模型并不陌生,在初中階段已有所了解.高中數學涉及的函數模型更為深入,難度更大,授課中應注重該種模型的應用講解.一方面,構建函數模型的關鍵在于找到自變量和因變量之間的關系,因此要求學生應用該模型進行解題時應認真審題,充分理解題意,尤其準確確定自變量的取值范圍,以保證解答的正確性.另一方面,為學生講解常見函數模型解答方法,如二次函數、指數函數、三角函數、高次函數等相關模型,使其認識到解題中通常需要借助函數的單調性進行求解,其中高次函數模型,則需要用到導數知識.
例1有一片樹林現有木材儲蓄量為7100cm3,要力爭使木材儲蓄量20年后翻兩番,達到28400cm3.
(1)求平均每年木材儲蓄量的增長率;
(2)如果平均每年增長率為8%,幾年可以翻兩番?
認真分析可知,解答該題目需要用到指數函數模型.對于(1)可設增長率為x,根據題意可構建如下模型:7100(1+x)20=28400,即(1+x)20=4.由對數知識可知,20lg(1+x)=2lg2,即,lg(1+x)≈0.0301,∴x+1≈1.072,所以x≈0.072=7.2%.(2)設y年可以翻兩番,則構建模型為:7100(1+0.08)y=28400,解得y≈18.02,即十八年后可以翻兩番.通過該題的講解使學生認識到,構建函數模型要認真審題,找到關鍵字構建對應數據模型.
二、把握特點,構建數列模型
數列模型是高中數學中較為常見的模型,包括等差數列和等比數列兩種類型.應用該種模型解答數學問題時,判斷是等比數列還是等差數列模型尤為關鍵.一方面,為學生總結等差數列和等比數列模型特點,使其認清兩種模型之間的區別,結合題干找到首項、公差或公比.另一方面,解答數列模型時,應積極回顧所學的數列知識,包括前n項和、數列的單調性,尤其注意在求解等比數列前n項和時,應注重按照公比q=1和q≠1兩種情況進行分類討論.
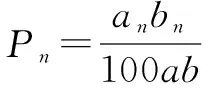
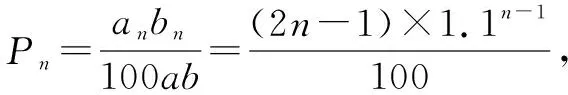
三、鼓勵想象,構建空間模型
立體幾何是高考的重要知識點,對學生空間想象能力要求較高.解答相關試題時構建合理的空間模型尤為重要.為使學生靈活應用空間模型解答立體幾何試題,一方面,可運用多媒體技術,從不同角度向學生展示立體幾何圖形,加深其對立體幾何點、線、面要素的認識;同時鼓勵學生聯想生活中的立體幾何圖形,合理想象,在頭腦中心形成清晰的空間對象.另一方面,要求學生具體問題具體分析,在求解的過程中,使用常規解法或向量解法,不斷提高空間模型解答能力.
例3已知△ABC是等腰直角三角形,∠C=90°,點M在△ABC外,且MB=1,AC=2,則MA的最大值是____.
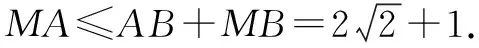
通過該題目的講解使學生認識到,構建空間模型時應選擇合適的視角,才能簡化計算,提高解題效率.
四、深思熟慮,構建概率模型
概率模型是高中數學的重要模型之一,相關試題難度并不大,但仍有一些學生在解題中出錯,因此為提高學生的概率模型應用能力,一方面,為學生講解常見概率模型,包括古典概型和幾何概型,使其充分理解兩種模型之間的區別,以及應用注意事項,如分析古典概型時,應注重當情況不確定時應注重分類討論,保證考慮問題的全面性.另一方面,構建概率模型時,可圍繞具體的問題情景,要求學生深思熟慮,認真分析,不斷鍛煉學生的模型分析以及構建能力.
例4某單位有3項業務要招標,共有5家公司前來投標,且每家公司對3項業務發出了投標申請,最終發現每項業務都有且只有一家公司中標.如果5家公司在各項業務中目標的概率均相等,問這3項業務由同一家公司中標的概率為多少?
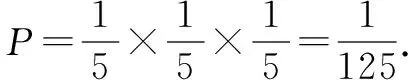
綜上所述,數學建模是一項重要的數學能力,根據題意構建正確的數學模型可明顯提高解題效率,因此授課中應提高認識,結合高中數學所學的數學模型,為學生認真細致地講解數學建模專業知識.同時創設相關的問題情景,對學生進行模型構建訓練,積累數學建模經驗與技巧,不斷提高數學解題能力.

