兩種橫向加速度計算方法對集裝箱系固的影響

(上海船舶研究設計院，上海 201203)

關于集裝箱系固設計中的加速度計算，各方法的計算結果存在明顯差異[1-3]。隨著近年來理論計算方法和CFD技術的飛速發展，各船級社均致力于追求更精確和更經濟的結果，持續地更新加速度計算方法。以中國船級社(CCS)規范為例，2009～2017年間共提出了3種集裝箱系固加速度計算方法。其中最新的計算方法由CCS《鋼質海船入級規范》2017修改通報(以下簡稱《CCS-2017》)提出。相對于此前由CCS《鋼質海船入級規范》2012提出的計算方法(以下簡稱《CCS-2012》)，《CCS-2017》采用了全新的封閉式計算體系，即不再提供具體的經驗公式和計算流程，而代之以通過CCS船舶計算系統進行擬合確定。

《CCS-2012》向《CCS-2017》的轉變被認為在大型集裝箱船系固安全和效率之間取得了新的平衡[4]，與德國勞氏船級社(GL)2013年規范中關于橫向加速度計算方法的轉變類似，與《GL-2007》相比，《GL-2013》得到的橫向加速度明顯偏低，甲板上集裝箱最大堆重顯著增加，堆重分布更加合理[5-6]。而關于CCS規范計算方法的轉變對不同級別集裝箱船系固設計的具體影響，目前未見報道。為此，擬通過具體算例對《CCS-2012》和《CCS-2017》進行對比，分析2種方法對不同級別集裝箱船系固設計的影響，并進一步探討《CCS-2017》中船型參數對橫向加速度及最大堆重的影響。

1 兩種橫向加速度計算方法

考慮到甲板上集裝箱對系固安全的要求更高，選擇甲板上集裝箱為研究對象。

《CCS-2012》中用于系固計算的橫向加速度at為

(1)

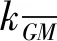
(2)

式中：L為船長；x為計算點至尾垂線的距離。按式(1)計算得到的at值應不小于CCS規范結構強度直接計算方法中定義的合成橫向加速度值。

《CCS-2017》規定的用于系固計算的橫向加速度at為

at=(g+bv)·sinφm+bh·cosφm+

(3)

式中：g為重力加速度；bv為由縱搖和升沉引起的垂向運動的加速度；bh為由艏搖和橫蕩引起的橫向運動的加速度；φm為船舶橫搖角；TR為船舶橫搖周期；z為集裝箱重心位置距基線高度；zROLL為船舶橫搖中心線距基線高度。bv、bh、φm及TR由CCS船舶計算系統根據船型參數進行計算。

從式(1)和式(3)可以看出，在其他條件一定的情況下，《CCS-2012》中的橫向加速度僅與集裝箱在船上的縱向位置有關，與垂向和橫向位置無關；而在《CCS-2017》中，同一縱向位置的集裝箱的橫向加速度隨z值增加而增大，這是更貼近實際情況的。

2 計算方案

2.1 不同船型對比計算方案

選取700、1 100、1 900、2 400及4 200 TEU 5型集裝箱船為研究對象，在每型船的甲板上選取距艉垂線0.1L、0.3L、0.5L、0.7L和0.9L5個縱向位置。分別應用《CCS-2012》和《CCS-2017》對每一船型每一縱向位置上的20 ft和40 ft集裝箱堆垛進行系固計算，得到100個用于計算的堆垛模型。主要船型參數見表1。

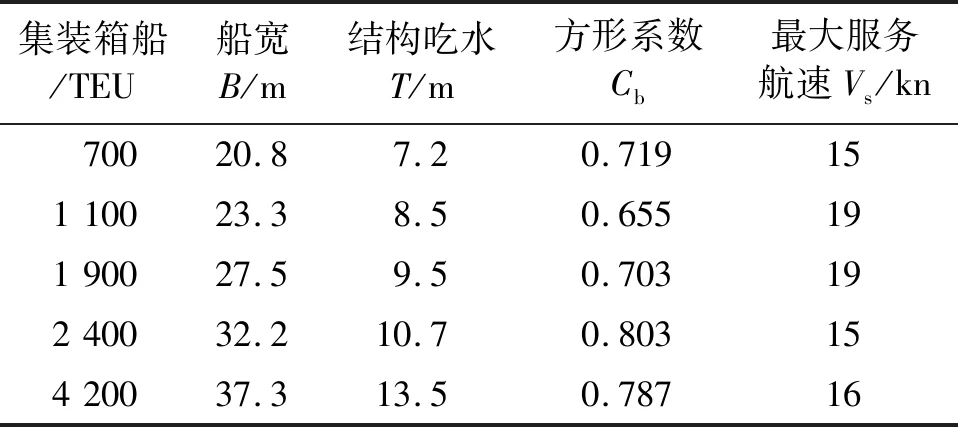
表1 研究對象的主要船型參數

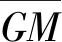
圖1 研究對象的系固布置方案

2.2 變船型參數計算方案

為探討《CCS-2017》中船型參數對橫向加速度及最大堆重的影響，選取4 200 TEU集裝箱船為研究對象，選取方形系數Cb、最大服務航速V和船寬B這3個船型參數作為研究變量。其中，Cb的取值點為0.65、0.70、0.75、0.80；V的取值點為16、18、20、22 kn；B的取值點為32.2、34.8、37.3、40 m。上述船型參數的取值范圍可覆蓋本級別集裝箱船中的巴拿馬型、寬體型和內貿型3種典型船型。

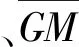
3 兩種方法對不同船型的影響

3.1 橫向加速度計算結果分析

采用《CCS-2012》和《CCS-2017》對2.1的計算方案展開計算，得到5型集裝箱船的橫向加速度at。定義堆垛高度中心位置的橫向加速度為堆垛的平均橫向加速度ata，用于反映堆垛整體的橫向加速度水平。計算結果見表2。

表2的結果反映出《CCS-2012》中橫向加速度與集裝箱垂向位置無關、而《CCS-2017》中橫向加速度隨集裝箱垂向位置增加而增大的總體特征，同時表明：

1)隨著船舶尺度的增大，2種方法計算得到的橫向加速度都呈現下降的趨勢。這與文獻[3]的結論是一致的。

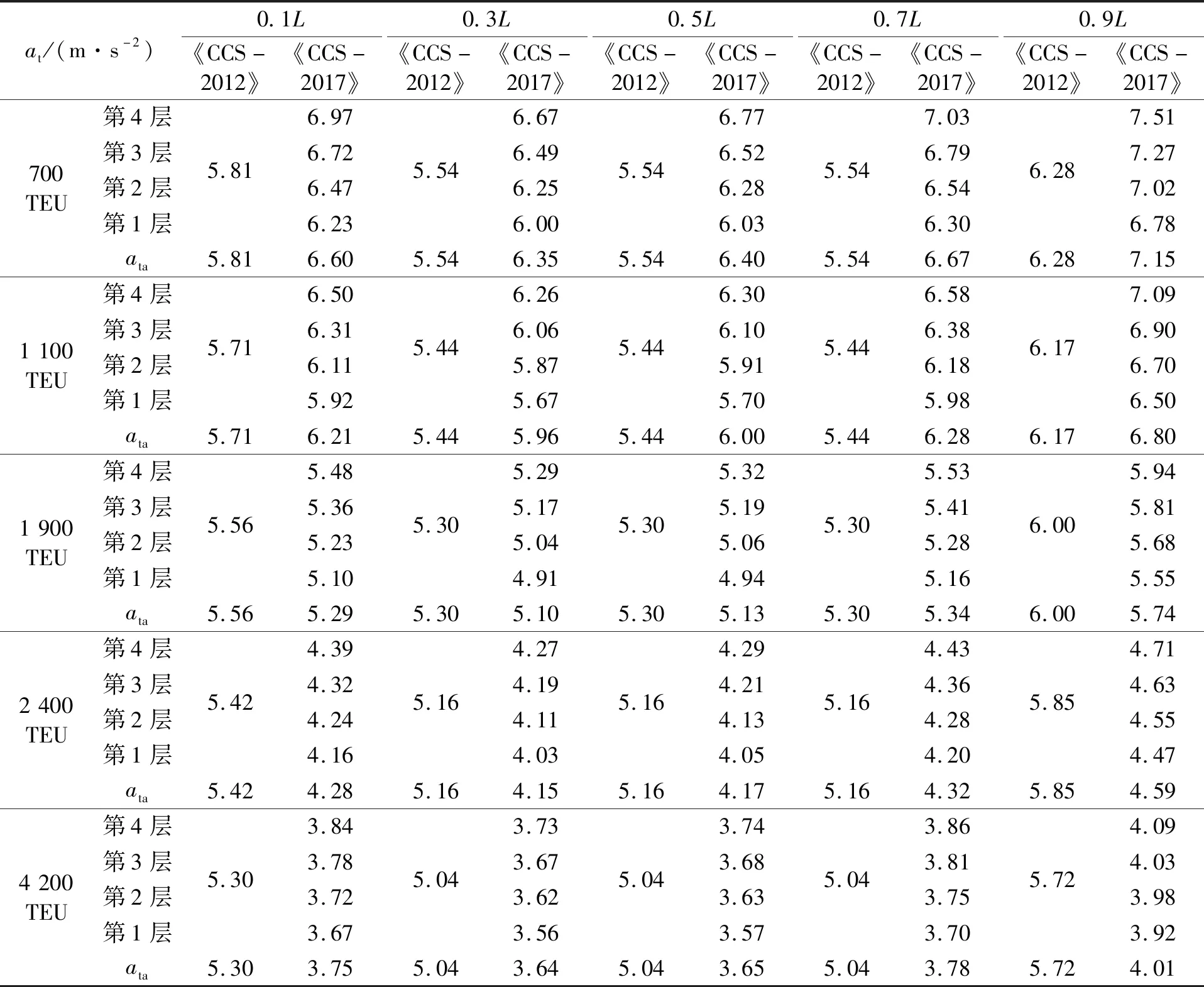
表2 橫向加速度計算結果

2)縱向位置上《CCS-2017》計算得到的橫向加速度最小值出現在距尾垂線0.3L位置附近，0.3L～0.9L范圍內橫向加速度遞增。這與《CCS-2012》中橫向加速度在距尾垂線0.2L～0.7L范圍內保持恒定是不同的。

根據表2中的結果，對比同一船型不同縱向位置的平均橫向加速度及不同型同一縱向位置的平均橫向加速度發現：

1)2種方法對1 900 TEU集裝箱船平均橫向加速度的計算結果相差不大；對于700、1 100 TEU集裝箱船，《CCS-2012》計算得到的平均橫向加速度略低于《CCS-2017》；對于2 400、4 200 TEU集裝箱船，《CCS-2017》計算得到的平均橫向加速度顯著低于《CCS-2012》。可見《CCS-2017》對船舶尺度大于1 900 TEU級的中、大型集裝箱船的系固設計有利。

2)從表2中每層集裝箱的橫向加速度計算結果可知，對于700、1 100 TEU集裝箱船，2種方法計算得到的橫向加速度的差異隨層數遞增而增大，隨船型增大而減小，《CCS-2017》計算得到的高層集裝箱的橫向加速度大幅高于《CCS-2012》。表明《CCS-2017》將為船舶尺度小于1 900 TEU級的小型集裝箱船的系固設計帶來一定的挑戰。

3)《CCS-2017》計算得到的平均橫向加速度隨船舶尺度的增大快速下降，而《CCS-2012》計算得到的平均橫向加速度隨船舶尺度的增大僅小幅降低；對于2 400、4 200 TEU集裝箱船，2種方法計算結果的差異隨船舶尺度的增長呈擴大趨勢。由此判斷，對于船舶尺度大于1 900 TEU級的集裝箱船，隨著船舶尺度的增加，采用《CCS-2017》所獲得的橫向加速度相對于《CCS-2012》的降低幅度越大。

3.2 最大堆重計算結果分析

根據3.1的橫向加速度計算結果對2.1的計算方案進行系固計算，得到5型集裝箱船20 ft集裝箱堆垛和40 ft集裝箱堆垛的最大堆重SWmax計算結果，見表3。

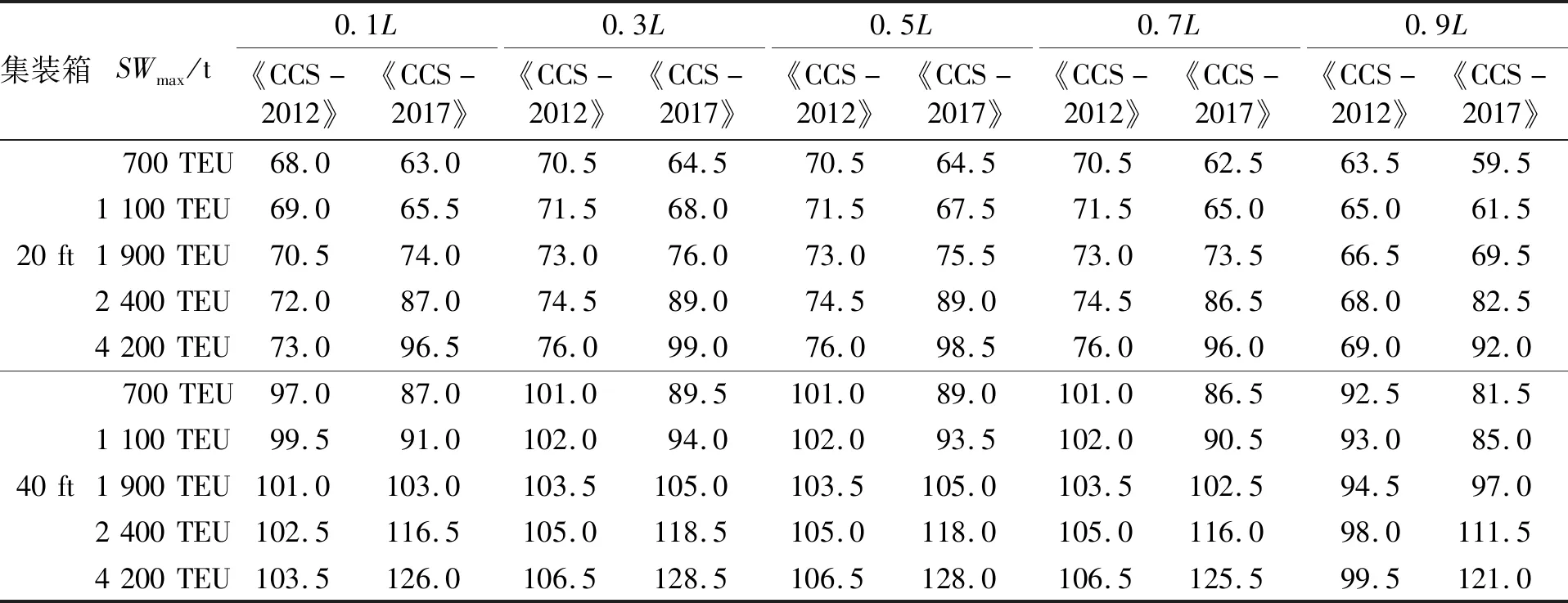
表3 20 ft集裝箱堆垛最大堆重計算結果

分析表3的計算結果可知：

1)2種方法對1 900 TEU的最大堆重計算結果接近；對于700、1 100 TEU集裝箱船，《CCS-2012》計算得到的最大堆重略高于《CCS-2017》；對于2 400、4 200 TEU集裝箱船，《CCS-2017》計算得到的最大堆重顯著高于《CCS-2012》。顯而易見，采用《CCS-2017》有利于提高大中型集裝箱船系固系統的堆重能力，這一點印證了文獻4的觀點；但小型集裝箱船系固系統的堆重能力將因采用《CCS-2017》而受到一定損失。

2)《CCS-2017》計算得到的最大堆重隨船舶尺度的增大快速增加，而《CCS-2012》計算得到的最大堆重隨船舶尺度的增大僅小幅增加；對于2 400、4 200 TEU集裝箱船，2種方法計算結果的差異隨船舶尺度的增長呈擴大趨勢。由此判斷，對于船舶尺度大于1 900 TEU級的集裝箱船，隨著船舶尺度的增加，采用《CCS-2017》所獲得的堆重優勢越大。

4 船型參數對《CCS-2017》計算結果的影響

4.1 方形系數

根據2.2中的計算方案，針對Cb=0.65、0.70、0.75、0.80這4種情況，分別應用《CCS-2017》對分別位于距艉垂線0.1L、0.3L、0.5L、0.7L和0.9L共5個縱向位置的20 ft集裝箱堆垛進行系固計算，結果見表4。

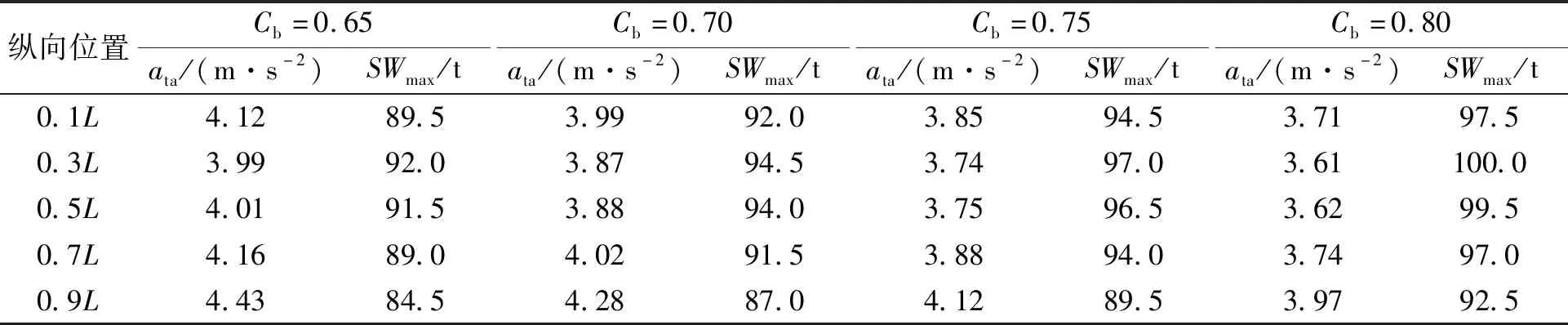
表4 不同方形系數情況下的ata和SWmax計算結果

表4表明，隨著方形系數的增大，平均橫向加速度呈下降趨勢，最大堆重呈上升趨勢。當方形系數由0.65增大到0.80時，距艉垂線0.1L～0.9L這5個縱向位置的平均橫向加速度分別降低了9.9%、9.6%、9.7%、10.0%和10.5%，而最大堆重分別增加了8.9%、7.0%、8.7%、9.0%和9.5%。由此認為，方形系數增大對《CCS-2017》的計算結果存在較大的有利影響。

4.2 服務航速的影響

根據2.2中的計算方案，針對Vs=16、18、20、22 kn 4種情況，分別應用《CCS-2017》對分別位于距艉垂線0.1L、0.3L、0.5L、0.7L和0.9L這5個縱向位置的20 ft集裝箱堆垛進行系固計算，計算結果見表5。

表5 不同航速情況下的ata和SWmax計算結果

表5表明，隨著航速的增加，平均橫向加速度呈微弱上升趨勢，最大堆重呈微弱下降趨勢。當航速由16 kn增大到22 kn時，距尾垂線0.1L～0.9L這5個縱向位置的平均橫向加速度分別僅增加了2.2%、1.5%、1.6%、2.2%和3.4%，而最大堆重分別下降了1.6%、1.6%、1.1%、2.2%和2.9%。由此認為，航速增加對《CCS-2017》的計算結果存在微弱的負面影響。

4.3 船寬的影響

根據2.2中的計算方案，針對B=32.2、34.8、37.3、40.0 m 4種情況，分別應用《CCS-2017》對分別位于距艉垂線0.1L、0.3L、0.5L、0.7L和0.9L這5個縱向位置的20 ft集裝箱堆垛進行系固計算，見表6。

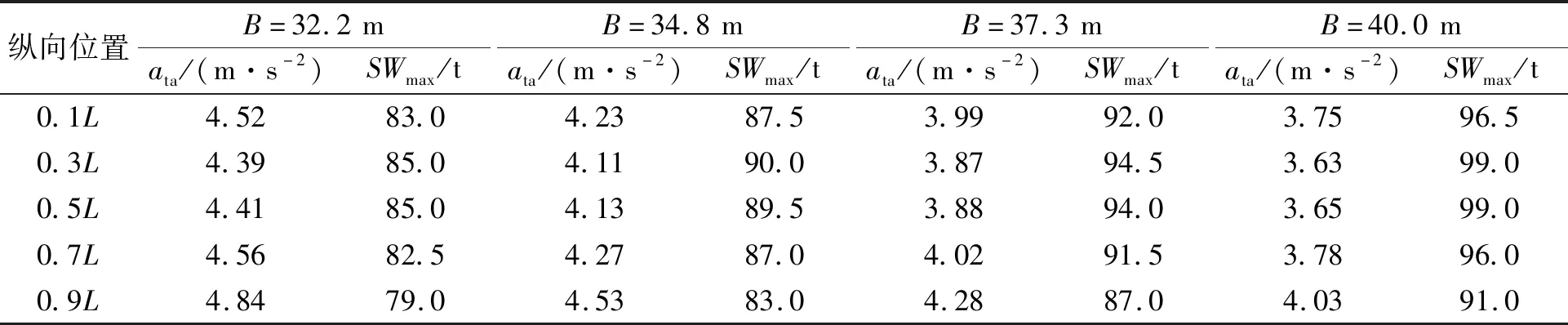
表6 不同船寬情況下的ata和SWmax計算結果

表6表明，隨著船寬的增加，平均橫向加速度呈下降趨勢，最大堆重呈上升趨勢。當船寬由32.2 m增大到40.0 m時，距尾垂線0.1L～0.9L這5個縱向位置的平均橫向加速度分別僅下降了17.1%、17.1%、17.3%、17.1%和16.7%，而最大堆重分別增加了16.3%、16.5%、16.5%、16.4%和15.2%，變化幅度超過了式(1)所反映的《CCS-2012》中橫向加速度與船寬的變化關系。由此認為，船寬增加對《CCS-2017》的計算結果存在較顯著的有利影響。

對比上述方形系數和航速對計算結果的影響幅度可以認為，船寬是這3個船型參數中最主要的影響因素。

5 結論

1)與《CCS-2012》相比，《CCS-2017》對船舶尺度大于1 900 TEU級的集裝箱船的系固設計有利；但將給船舶尺度小于1 900 TEU級的小型集裝箱船的系固設計帶來不利影響。

2)對于船舶尺度大于1 900 TEU級的集裝箱船，隨著船舶尺度的增加，《CCS-2017》對集裝箱系固的優勢越明顯。

3)方形系數、航速、船寬對《CCS-2017》的橫向加速度及最大堆重計算結果存在一定影響，其中船寬是最主要的影響因素。

計算結果顯示，《CCS-2017》使4 200 TEU及以上的集裝箱船獲得超過90 t的無綁扎堆重(20 ft集裝箱堆垛)、超過120 t的雙層綁扎堆重(40 ft集裝箱堆垛)，使得20 ft集裝箱堆垛不綁扎、40 ft集裝箱堆垛兩端無綁扎橋這一常規系固設計方案的潛力得以充分發揮，這對于優化中型集裝箱船的總布置、提高經濟性具有重要意義。