艦用膜式氣囊隔振器剛度特性計算方法

(海軍工程大學a.振動噪聲研究所;b. 船舶振動噪聲重點實驗室,武漢 430033)

氣囊隔振器已經廣泛應用于艦船隔振系統中[1-3]。氣囊隔振器主要有囊式和膜式兩種結構，目前艦船隔振系統中主要采用囊式結構氣囊隔振器，膜式結構氣囊尚主要應用于車輛領域，工作壓力較低。與車用氣囊相比，艦用氣囊隔振器工作壓力增加約5倍，為提高可靠性，其囊體內部一般會設置更多簾線層以及選用更高強度的簾線。

對于膜式氣囊的力學特性，國內外的研究工作[4-8]皆認為氣囊的承載力僅取決于囊內壓力和氣囊幾何形狀，并在此基礎上展開氣囊剛度特性分析。由于并未考慮囊體對氣囊力學特性的影響，由此計算得到的剛度特性并不準確，尤其是對于囊體強度顯著增強的艦用膜式氣囊隔振器，其設計誤差相對較大。為此，依據薄殼理論建立膜式氣囊隔振器力學模型，推導出含有間隙系數δ的承載力表達式，并在此基礎上展開剛度特性分析，對現有膜式氣囊的剛度特性計算方法進行修正。

1 理論建模

艦用膜式氣囊隔振器主要由上蓋板、約束套筒、囊體和底座組成。見圖1，建立膜式氣囊隔振器力學模型。由幾何結構模型可得R1，R2和R3間的函數關系為

(1)

因氣囊隔振器囊體厚度相對較薄，并且受到剪力和彎矩易變形，根據薄殼理論進行分析，不考慮與金屬套筒接觸的囊體部分，由此建立氣囊平衡方程、物理方程和邊界條件。

(2)

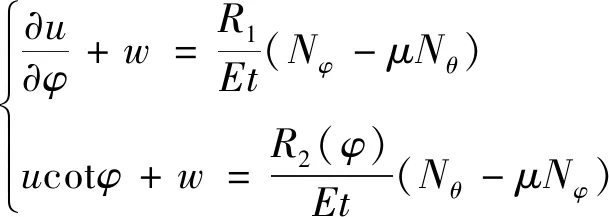
(3)

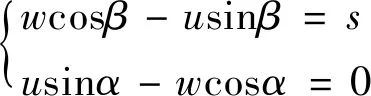
(4)

由于囊體中簾線的彈性模量遠遠大于橡膠的彈性模量，且簾線在整個復合材料中所占體積非常小，因此認為囊體的宏觀彈性模量由簾線決定，而其泊松比由橡膠材料決定。因此，囊體物理方程(3)中的E為簾線的彈性模量；t為簾線總厚度；μ為橡膠的泊松比。

假定氣囊在額定高度附近某一高度工作，則邊界條件(4)中的s即為氣囊工作高度距額定高度的位移。

2 承載力計算

如圖2所示，將殼體沿平行圓切開，根據內力平衡求出經向線應力Nφ再結合式(2)即可解得囊體的內力表達式為

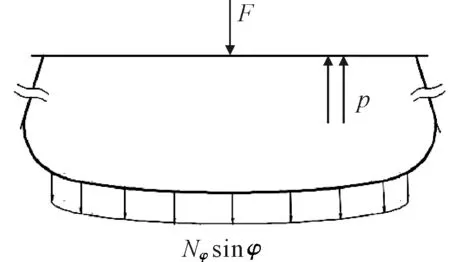
圖2 氣囊內力平衡分析

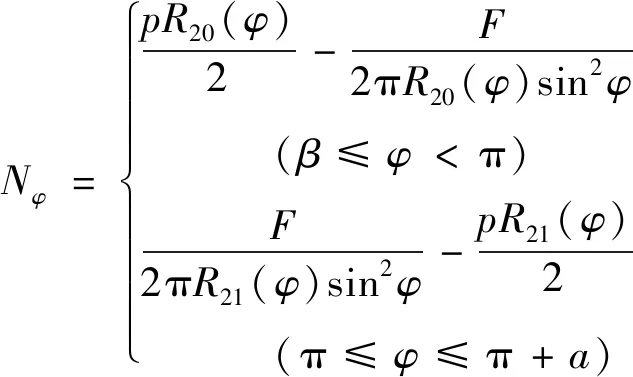
(5)

以薄殼理論建立的膜式氣囊隔振器模型實質上是一種軸對稱圓環殼，假設φ=π對應此模型上的點為V，則V點及其附近一定存在彎曲應力，由于囊體的平衡方程(2)中并未考慮彎曲應力的影響，因此，在φ趨近于π時，在V點附近求解出的內力值Nφ和Nθ接近于無窮大，此時計算誤差較大，需要進行修正。

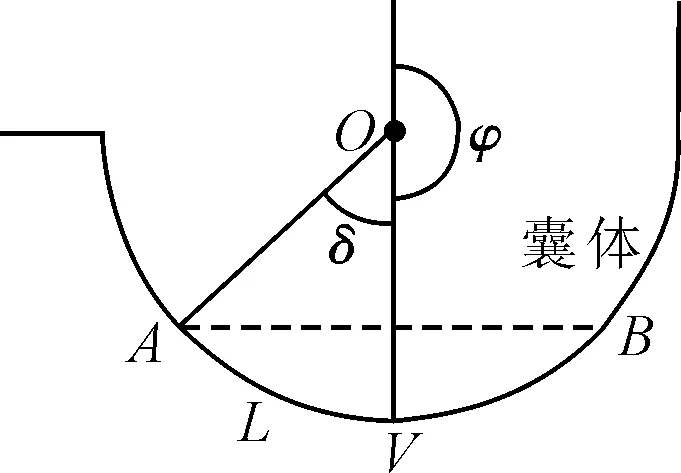
圖3 間隙系數δ示意

如圖3所示，在囊體上分別設置距點V弧長為L的兩點A,B。

假定間隙系數δ為弧長L對應的弧度值，以點A,B處的內力計算值分別近似代替圓弧AV和VB上各點處的內力計算值，即可得到修正后的內力表達式為

(6)

將囊體內力表達式代入囊體物理方程(3)求解出囊體位移表達式，再根據囊體邊界條件(4)即可求解出氣囊隔振器的承載力表達式為

(7)

式中：Ii(φ)(i=1,2,…,8)是與氣囊結構參數有關的方程，表達式為

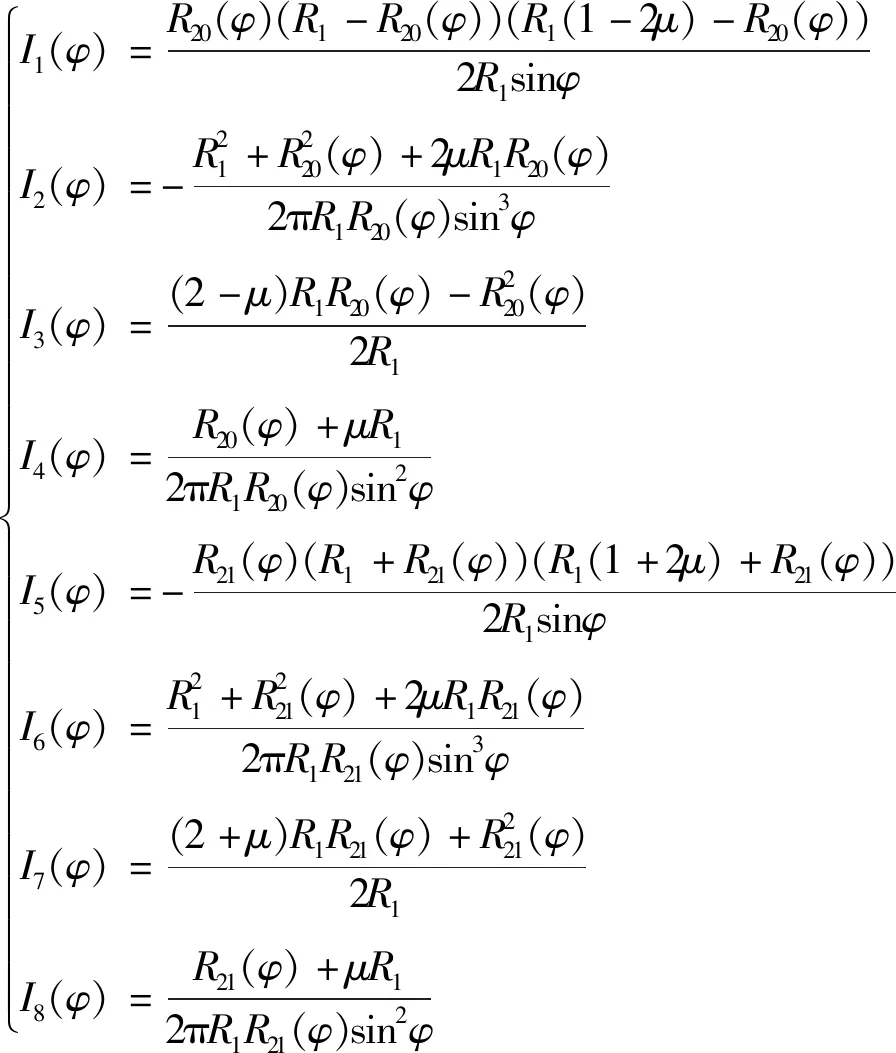
(8)

當間隙系數δ=0時，式(8)可化簡為

F=p·πR23

(9)

此時，氣囊隔振器的承載力僅與囊內氣壓以及結構參數R3有關，與囊體材料特性無關，此即為現有理論設計模型中所應用的承載力計算式。

3 剛度特性計算

氣囊剛度特性計算，實質上就是計算氣囊在兩種工作高度之間承載力變化與位移的比值。假設氣囊在距額定高度為s0的高度H0處，將氣囊拉伸至高度H1，此時距額定高度為s1，承載力為G1；將氣囊壓縮至距額定高度為s2的高度H2處，承載力為G2。3個高度偏移值之間的關系為

s1+s2=2s0

(10)

則氣囊在高度H0處的剛度值為

(11)

由于氣囊的結構參數R1，R3，以及氣壓p會隨著工作高度的變化發生改變，因此，參照文獻[9]建立R1，R3，p與工作高度之間的函數表達式。再結合式(7)和式(10)即可求解出氣囊在不同高度下的剛度值。

4 間隙系數經驗表達式

在上述求解氣囊隔振器剛度特性的計算方法中，間隙系數δ的理論值尚不能確定，因此，通過試驗確定間隙系數δ的經驗表達式。

采用某型艦用膜式氣囊隔振器進行試驗，試驗安裝結構見圖4，樣機參數見表1。

圖4 氣囊試驗安裝結構示意

表1 氣囊樣機參數

注：H′0-氣囊隔振器的額定工作高度；V′0-氣囊隔振器的初始容積，用以確定氣壓p與工作高度之間的函數關系。

氣囊樣機通過螺栓固定于試驗機上下夾頭處，試驗過程中上夾頭固定，通過緩慢移動下夾頭改變氣囊高度，由計算機輸出位移值和力傳感器值。通過三次多項式擬合試驗數據，得到承載力與高度之間的關系式，對關系式求導即可求解出氣囊在不同工作高度下的剛度特性試驗值[10]。

選取20組該型艦用膜式氣囊隔振器，在額定氣壓下進行剛度特性試驗。由于艦用氣囊隔振器的變形較小，因此,其剛度特性試驗中的峰峰值一般設置為7 mm。以額定高度(H′0±3.5) mm處承載力的平均變化值作為剛度特性參考值，分別計算當各組氣囊隔振器剛度特性參考值與理論計算值基本相等時，理論計算模型中的間隙系數δ的對應數值。由試驗及計算得到20組間隙系數的平均值δ′為0.28。

間隙系數實際上是修正理論模型中，為規避彎曲應力截取的弧長L所對應的弧度值。假定不同型號的氣囊隔振器所截取的弧長L為定值，根據上述試驗結果可計算得到弧長的經驗值為L′=δ′R′1=0.042。

由此可得到氣囊隔振器間隙系數δ的經驗表達式為

(12)

式中：R1為不同型號氣囊隔振器的波紋半徑。

5 適用性驗證

為驗證剛度特性計算方法以及間隙系數經驗表達式的正確性，選取另一型氣囊進行驗證，樣機參數見表2。

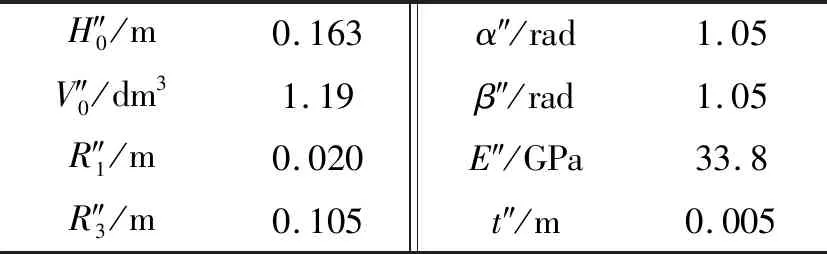
表2 氣囊樣機參數

由間隙系數的經驗表達式(12)可計算出此型艦用膜式氣囊間隙系數δ為0.21,將其帶入修正后的理論模型，其剛度特性計算和試驗結果見圖5。當δ=0時(即現有理論計算模型，其未考慮囊體材料特性影響)，剛度特性計算平均誤差為29.58%;當δ=0.21時,其剛度特性計算平均誤差為6.13%，此時剛度特性計算誤差大大降低，能夠滿足設計精度需求。

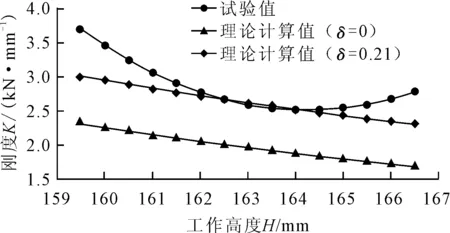
圖5 不同工作高度下的剛度特性試驗及理論計算值

6 囊體材料特性的影響

以囊體結構參數λ表征囊體材料特性，參數λ為簾線彈性模量E與簾線總厚度t的乘積。

λ=Et

(13)

在λ不同的情況下計算修正前后理論模型的剛度特性參考值。計算結果見圖6。當參數λ≤107N/m時，間隙系數δ=0.21和δ=0時的剛度特性計算值基本一致，修正前后的理論計算模型基本一致。但是當λ≥107N/m時，隨著λ的增大，修正前后理論模型計算值偏差將越來越大，現有理論模型的計算精度將難以滿足要求。

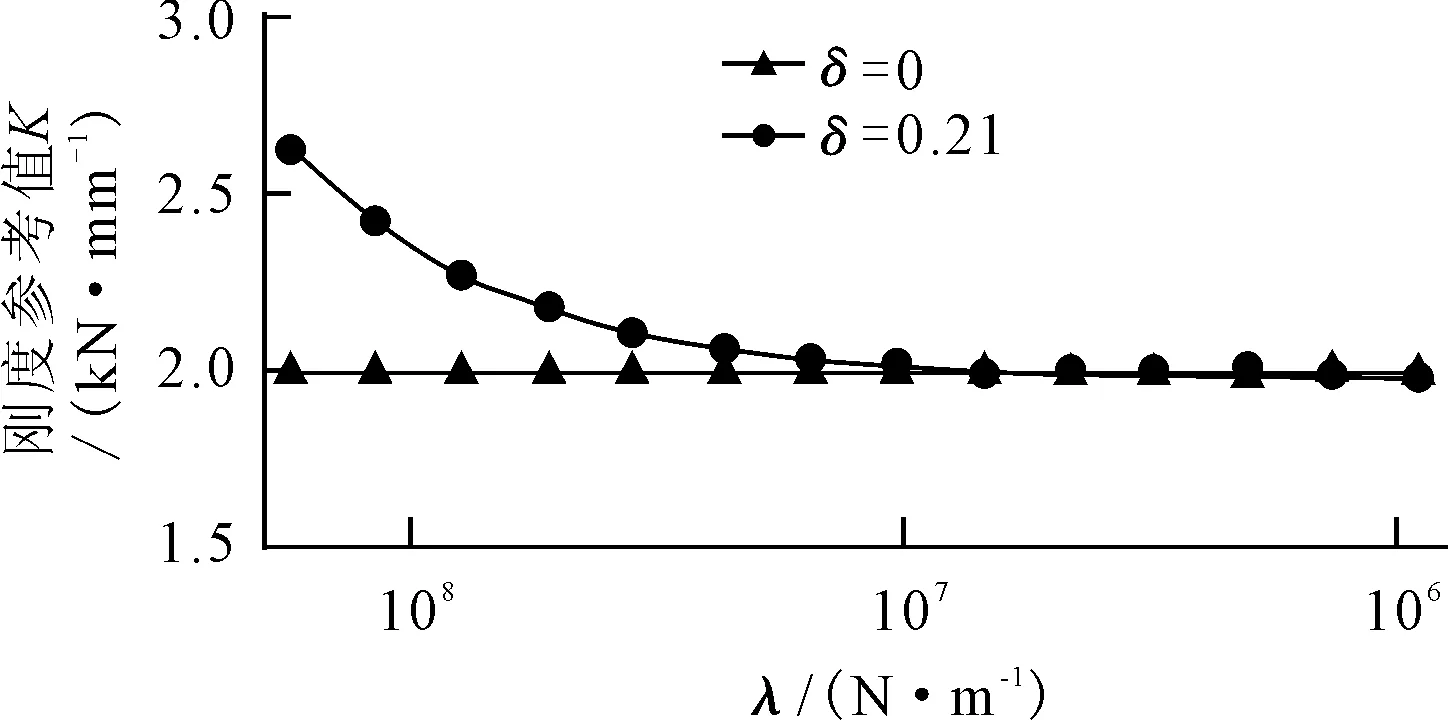
圖6 不同間隙系數下剛度特性參考理論計算值

車用膜式氣囊隔振器囊體簾線骨架層常選用尼龍簾線，囊體內部一般鋪設兩層簾線，尼龍簾線的彈性模量一般為1.4 GPa，直徑一般為0.53～0.78 mm[11-12]，故車用膜式氣囊的參數λ值可近似為7.42×105～2.18×106N/m。

因此，現有理論設計模型能夠滿足車用膜式氣囊的計算精度，但是對于囊體強度大大增強的艦用膜式氣囊隔振器，λ一般大于108N/m，因此必須對現有理論計算模型進行修正以滿足艦用膜式氣囊的剛度特性計算精度。

7 結論

1)提出一種較為合理的艦用膜式氣囊隔振器的剛度特性計算方法，修正后的理論計算模型能夠有效提高艦用膜式氣囊隔振器的剛度特性計算精度。

2)采用試驗的方法得到間隙系數表達式，具備一定的適用性。但是尚需明確其在修正模型中的物理意義以及理論方程。此外，由于未考慮囊體材料的非線性，導致剛度特性的計算值隨著工作高度的變化，計算誤差也在逐漸變大。因此，需進一步研究囊體材料的精確理論模型。