非均勻波導中的聲聚焦

郭威 楊德森1)2)?

1) (哈爾濱工程大學, 水聲技術重點實驗室, 哈爾濱 150001)

2) (海洋信息獲取與安全工業和信息化部重點實驗室(哈爾濱工程大學), 哈爾濱 150001)

3) (哈爾濱工程大學, 水聲工程學院, 哈爾濱 150001)

理論研究了聲波在非均勻波導中的空間聚焦問題, 利用多模態導納法構建波導內任意位置處聲壓與入射聲壓在模態域的映射關系, 計算使聲波聚焦于空間某位置時的最佳入射波, 并畫出了相應的聚焦聲場.研究了三種非均勻情況: 水平變截面波導、含散射體波導以及聲速垂直變化波導.結果表明, 當輸入最佳入射波時, 在非均勻波導中可以產生良好的單點或多點聲聚焦效果, 聲波的聚焦過程充分地利用了波導結構及介質非均勻性對聲波的散射作用.

1 引 言

聲波聚焦在聲通信、聲成像、無損檢測以及超聲醫學治療等領域具有重要的應用價值.目前實現聲波聚焦的一種手段是設計特殊的材料和結構, 例如二維聲子晶體[1]、聲透鏡[2,3]、負折射聲超構材料[4]等, 或借助熱聲學手段[5,6], 改變傳播介質的折射率, 控制聲波的傳播路徑, 實現空間聚焦.該方法已在均勻自由場中產生了良好的聲聚焦效應.然而, 對于聲波在非均勻波導中的傳播, 由于介質本身的不均勻性及邊界的散射作用, 傳播過程較自由場中復雜, 控制聲波的傳播路徑也相對困難, 較難應用該手段實現非均勻波導中的聲聚焦.另一種研究波聚焦的方法為相位共軛法(phase conjugation),首先應用于光學領域[7], 以實現光波穿過復雜散射區域后的空間聚焦.相位共軛法是基于絕熱物理系統的時間反轉不變性, 對點光源穿過散射區域后產生的透射波進行相位共軛(時間反轉)處理, 再將處理后的光波作為入射波, 反向穿過散射區域, 最終在原本的點光源位置處形成聚焦[8].此外, 很多學者將相位共軛法與透射矩陣[9,10]相結合, 實驗測量透射矩陣, 進而給出入射波, 使其穿過散射區域后直接產生空間聚焦[11,12]或時間空間同時聚焦[13?16].Fink等[17]將相位共軛法引申到聲學領域中, 稱為時間反轉法 (time reversal), 可實現聲波穿過非均勻介質后的空間聚焦[18], 其優點是無需介質的先驗信息即可完成自適應聚焦[19].但相位共軛法多為研究波穿過散射區域后的聚焦[8?18], 且依賴于實驗手段, 相對缺乏系統的理論分析, 而且對在散射區域內部實現聚焦的相關研究也較少.

鑒于上述問題, 本文從均勻剛硬波導入手, 進而研究水平變截面、含散射體以及聲速垂直變化三種非均勻波導內的聲聚焦問題.利用一種求解非均勻波導內聲場的半解析方法—多模態導納法[20],構建波導中任意位置處的總聲場與入射聲壓的映射關系, 給出聲波在該位置處聚焦, 即在該位置聲壓幅值達到最大值時的入射條件, 并畫出對應的聲場分布.

2 均勻波導內的聲聚焦

首先考慮二維笛卡爾坐標系下均勻剛硬波導中的聲聚焦問題.簡諧聲源(時間因子 e?iωt)位于x=0處.經由無量綱化處理其中 ρ ,c,h,ω,k 分別為介質密度、聲速、波導高度、角頻率及無量綱波數, x,y分別表示水平方向及垂直方向, 且(x,y)∈ [0,∞)×[0,1], 聲壓滿足無量綱亥姆霍茲方程?2p/?x2+?2p/?y2+k2p=0及邊界條件 ?yp|y=0,1=0.聲壓場的通解可寫為

本文研究的目的是計算單位輻射聲功率(入射聲能流)條件下, 在空間任意位置 ( x0,y0) 處獲得最大聲壓幅值的最佳入射波, 即計算 pi或 pi,n以獲得在均勻波導中, 由 (1)式可知, 當時, 聲壓在 ( x0,y0) 處獲得最大幅值, 其中上標“*”表示共軛, L 是聲能流的歸一化系數,即為最佳入射波.無量綱的入射聲能流表達式為

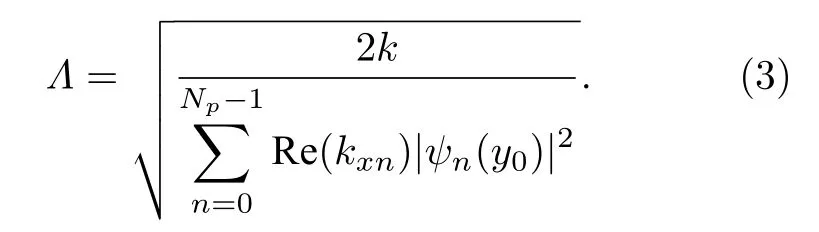
(3)式中 Np表示傳播模態數目, 為使不等式Np? 1+k/π成立的最大整數.聚焦點處的聲壓為

該聲壓即為給定頻率時, 在 ( x0,y0) 處可達到的聲壓幅值上界.由(4)式可知, 聚焦點處的聲壓主要來自傳播模態的貢獻, 衰逝模態的作用為保證該聲壓值在有限頻率下收斂.

圖1為均勻波導中, 入射波頻率為k=19.1π時, 在 ( x0,y0)=(3.2,0.4) 處產生聚焦的聲壓幅值分布.通過觀察發現, 當聚焦點距離邊界較遠時, 聚焦點附近的聲場與分離常量為0時的奇對稱Weber波束非常相似[21].聲波在均勻波導中的聚焦過程充分利用了邊界的反射作用.

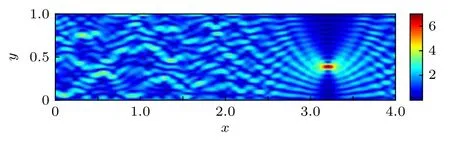
圖1 均勻波導中的聲聚焦Fig.1.Sound focusing in homogeneous waveguides.

另外, 從 (4)式可知, 當固定頻率以及 x0時,聚焦點處的聲壓僅由決定.根據余弦函數的周期性和偶對稱性可得

其中m為任意整數.( x0,±y0+2m) 可看作是聚焦點 ( x0,y0) 關于波導上下壁面對稱產生的虛聚焦點(類比虛源), 選擇虛聚焦點中任意一點研究聲聚焦時, 聲波仍會在 ( x0,y0) 處聚焦.

3 非均勻波導中的聲聚焦

在均勻波導的聲聚焦問題中, 首先建立了任意位置處聲壓與入射聲壓的展開系數的映射關系((1)式), 進而求解使 p (x0,y0) 達到極值的最佳入射波.在非均勻波導中, 聲場與入射波之間不再是簡單的單向傳播的映射關系, 本文采用多模態導納法 (multimodal admittance method)[20]建立任意位置聲壓與入射波的展開系數的映射算子, 進而研究產生聲聚焦的最佳入射波條件并求解聲場.本節討論水平變截面、含散射體以及聲速垂直變化三種非均勻波導中的聲聚焦現象.

3.1 水平變截面波導中的聲聚焦

圖2 水平變截面剛硬波導示意圖Fig.2.Configuration of rigid waveguides with varying cross-sections.

聲壓滿足的亥姆霍茲方程及邊界條件為

這里 ψn(x,y) 為局部本征函數, 對應均勻波導條件下上邊界等于局部高度 h (x) 時的本征函數, 其表達式為

其中 εn=2? δn0.然后, 將 (8)式代入 (6)式并投影到局部本征函數利用本征函數的正交性可得耦合偏微分方程組:

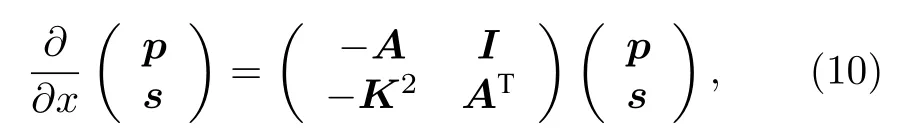
其中, p (x) 和 s (x) 分別為模態展開系數 pn和 sn組成的向量, 上標“T”表示轉置; I 為單位陣, K(x)為對角陣, 各元素為矩陣A 的表達式為

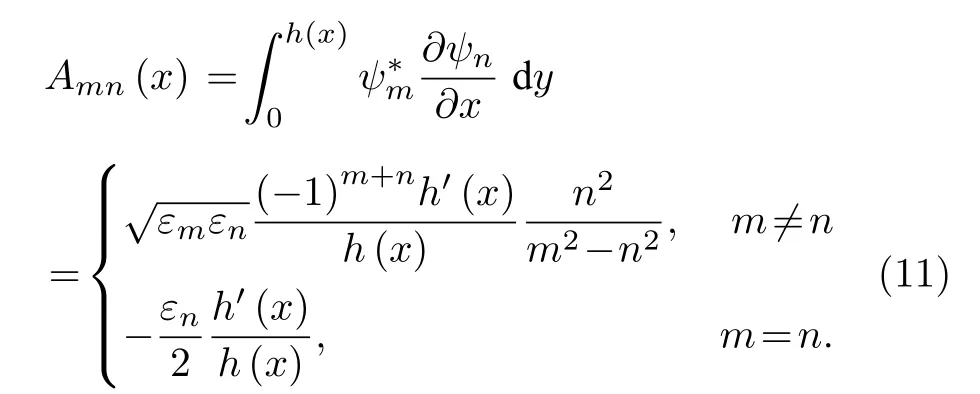
由(10)式, 聲場的求解問題轉化為耦合偏微分方程組的初值問題, 兩個初值條件為入射條件和輻射條件.然而根據輻射條件從右向左積分求解(10)式時, 由于衰逝模態從右向左是指數發散的,積分結果不收斂.因此引入導納矩陣Y, 以規避衰逝模態的指數發散問題[22,23], 穩定求解(10)式.導納矩陣的定義為 s =Yp , 代入(10)式, 求得導納矩陣滿足的Riccati方程:

Y的初條件為Y(x?xmax)=iK(xmax), 可從xmax至0積分求得任意x處的導納矩陣.為建立x處聲壓與入射波聲壓之間的映射關系, 引入傳播算子M(x), 定義為 p (x)=M(x)p(0).代入 (10)式可得傳播算子滿足的方程為 ?xM=(Y?A)M , 初條件為 M (0)=I , 從 0 至 xmax積分求解.導納矩陣Y和傳播算子M可利用四階Magnus積分格式進行數值計算, 詳細過程見文獻[24]和[25].

定義模態域的反射矩陣R滿足pr(0)=Rpi(0), 其中 pi(0),pr(0) 是 x =0 處的入射波和反射波聲壓的模態展開系數.x =0 處總聲壓的模態展開系數可寫為 p (0)=pi(0)+pr(0) , 又由s(0)=iK(0)(I?R)pi(0)=Y(0)p(0), 可得

定義透射矩陣T滿足pt(xmax)=p(xmax)=Tpi(0),其中 pt(xmax) 為 xmax處透射波聲壓的模態展開系數, 根據傳播算子 M (x) 的定義式, 可得

至此, 反射矩陣R, 透射矩陣T以及傳播算子M(x)均可計算.接著可以給出散射區域總聲壓的模態展開系數 pn(x)=M(x)(I+R)pi(0) , 以及透射區域聲壓的模態展開系數

再結合(8)式, 最終得到變截面波導內任意點(x0,y0)處聲壓與入射聲壓的模態展開系數 pi(0) 的映射關系:

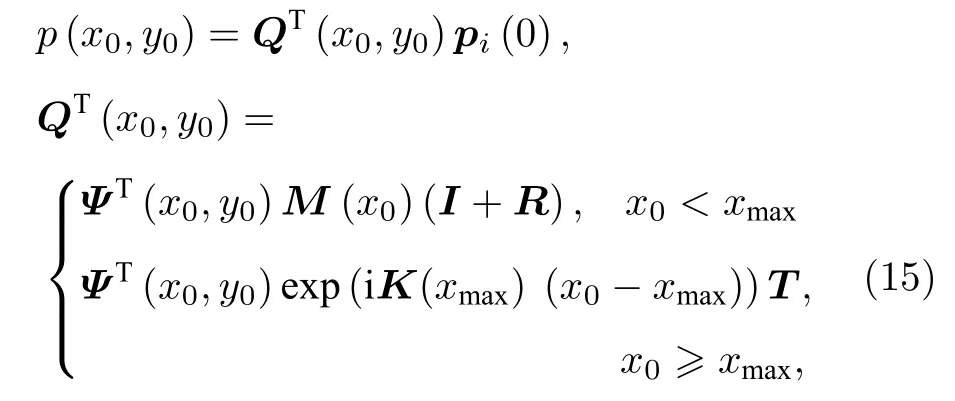
其中, QT(x0,y0) 為映射向量; Ψ(x0,y0)=[ψ0(x0,y0),ψ1(x0,y0),···,ψN?1(x0,y0)]T為 ( x0,y0) 處局部本征函數構成的向量; N為模態的截斷數, 要求N>max[Np(x)], 即截斷數的選取需大于波導中的傳播模態數量.(15)式可寫作希爾伯特空間中的向量內積形式, 即 p (x0,y0)= ?Q?(x0,y0), pi(0)? ,其中上標“H”代表共軛轉置.使內積結果最大的 pi(0) 就是在 ( x0,y0) 處產生聲聚焦的最佳入射波的模態展開系數, 即

其中 L為聲能流的歸一化系數, 計算方法見(2)式.因此, 最佳入射波可寫為

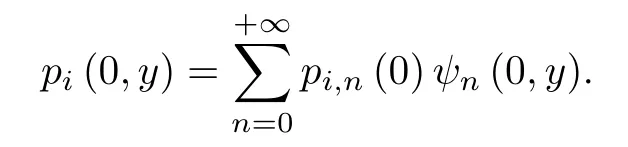
綜上, 可采用多模態導納法將復雜波導中的聲場求解問題轉化為計算模態域的展開系數問題, 再引入導納矩陣 Y (x) 和傳播算子 M (x) , 可以直接構建總聲場與入射波的展開系數的映射關系, 這種直接明確的映射關系將空間任意位置處的聲壓表示為映射向量 Q?(x0,y0) 與入射波模態展開系數pi(0)的內積的形式, 求解聲聚焦的問題最終轉化為求解使該內積((15)式)達到極值的最佳入射波問題.需要指出的是, 對于變截面波導, 本文選取的局部本征函數 ψn(x,y) 并不滿足實際的上邊界條件, 也就 是 ψn(x,y) 在 上邊 界滿 足的 邊 界 條 件 是?ψn/?y=0, 而不是真正的邊界條件 ? ψn/?n=0 ,這使(8)式的收斂速度不高( 1 /N2).文獻[26]提出了改進多模態導納法, 用以提高聲場解的收斂性(提高為 1 /N4).方法為構造一階新的本征函數ψ?1(x,y), 使之既與原局部本征函數 ψn(x,y)(n=0,1,···,N? 1)正交, 又在上邊界滿足非齊次Neumann邊界條件.但是, 由于構建的本征函數ψ?1(x,y)在傳播方向上表現為衰逝模態[26], 且由(4)式, 發現衰逝模態對聲聚焦的作用很小, 因此可忽略 ψ?1(x,y) 對聲聚焦的貢獻, 故本文選取的局部本征函數 ψn(x,y) 足夠滿足聲聚焦分析的要求.

總而言之, 對于非均勻波導, 只要求得散射區域內的導納矩陣 Y (x) 和傳播算子 M (x) , 進而得到反射矩陣R及透射矩陣T, 即可給出聲壓與入射聲壓的模態展開系數的映射關系, 最終計算在任意點產生聚焦的最佳入射波.

圖3給出了利用上述方法計算變截面波導中, 在不同位置處產生聚焦的聲場.入射波頻率為 k =29.1π , 波導上邊界表達式為h(x)=0.8+0.2cos(2πx/3), xmax=3.圖3(a)和 3(b)中的聚焦點分別位于透射區域和散射區域, 坐標為(x0,y0)=(3.2,0.9)及 ( 1.6,0.2).圖3(c)及圖3(d)插圖中的藍色實線分別對應圖3(a)及圖3(b)中的入射波形,均為由(16)式計算得到的最佳入射聲波, 黑色點線為平面入射波; 主圖中的藍色實線為固定 x0時,聲壓幅值隨高度的變化曲線, 即 | p (x0,y)| ; 黑色點線為入射波是平面波時, 對應的 | p (x0,y)|.如圖3所示, 當入射聲波是最佳入射波時, 不論聚焦點在散射區域還是透射區域, 聲波利用邊界的散射作用, 均在對應點處發生了聚焦, 并且聚焦點處的聲壓幅值明顯大于入射波是平面波時的聲壓幅值, 聚焦效果良好.

圖3 (a)和 (b)為變截面波導分別在 ( x0,y0)=(3.2,0.9) (透射區域)及 ( 1.6,0.2) (散射區域)處產生聚焦的聲場; (c)和 (d)主圖中的藍色實線分別為(a)和(b)中 x 0 處的聲壓幅值隨高度方向的分布, 黑色點線為 pi= Λψ0(y) (平面波)時 x0 處的聲壓幅值分布; 插圖中的藍色曲線和黑色點線分別為最佳入射波及平面波的幅值曲線Fig.3.Acoustic focusing field in the waveguide as calculated by the present method.The foci are located at (a) (x0,y0)=(3.2, 0.9) in transmission region and (b) ( 1.6,0.2) in scattering region, respectively.The blue solid lines in (c) and (d) are |p(x0,y)|corresponding to (a) and (b), respectively, and the black dotted lines are | p (x0,y)| generated by pi= Λψ0(y) (plane wave).The insets plot the modulus of the corresponding incident waves.

根據線性疊加原理, 可以實現非均勻波導中的多點聲聚焦.選取多個聚焦點位置, 利用(16)式分別獲得對應的最佳入射波.然后將這些入射波求和構建新的入射波并將其輸入至波導中, 對應聲場則產生多點聲聚焦效應.圖4(a)給出多點聲聚焦的聲場, 其中頻率的選取及波導結構與圖3一致, 聚焦點位于 ( 3.2,0.9) 及 ( 3.2,0.1).圖4(b)畫出了疊加后的總入射聲壓的幅值分布.圖4(c)中的黑色虛線、紅色點劃線和藍色實線分別為只在 ( 3.2,0.1) 處產生單點聚焦、只在 ( 3.2,0.9) 處產生單點聚焦和同時在 ( 3.2,0.1) 和 ( 3.2,0.9) 處產生雙點聚焦時x=3.2處的聲壓幅值隨y的分布.可以看出雙點聚焦時各個聚焦點處的聲壓幅值均低于單點聚焦的情況, 這是符合能量守恒定律的.雙點聚焦時各個聚焦點處的聲壓幅值均明顯大于其他位置處的聲壓幅值, 說明輸入計算得到的總入射波, 可以實現良好的多點聲聚焦效果.

3.2 含散射體波導中的聲聚焦

簡單起見, 考慮波導中僅存在一個散射體時的聲聚焦問題, 波導模型如圖5所示, 散射體邊界為[y=a(x),y=b(x)], 波導主介質的密度及聲速為ρ1,c1, 散射體內部介質的密度及聲速為 ρ2,c2, 且ρ1,ρ2,c1,c2均為常量.波導介質區域與散射體占據區域分別用 ?1和 ?2表示.聲壓滿足的無量綱亥姆霍茲方程為

其中, 波數 k =ωh/c1, 1 +η=c1/c2為折射率.邊界條件和連續性條件分別為

圖4 (a) 變截面波導中的雙點聚焦聲場, 聚焦點為 ( 3.2,0.9) 及 ( 3.2,0.1) ; (b) 最佳入射聲壓幅值分布; (c) 藍色實線為 (a) 中聲場在 x =3.2 處的聲壓幅值分布; 紅色點劃線表示聲波在 ( 3.2,0.9) 處單點聚焦時的聲壓幅值分布, 與圖3(c)中藍色曲線一致; 黑色虛線為聲波在 ( 3.2,0.1) 處單點聚焦時的聲壓幅值分布.頻率和波導幾何參數與圖3一致Fig.4.(a) Sound two-point focusing field in the waveguide with varying cross-section, the foci are located at ( 3.2,0.9) and(3.2,0.1); (b) modulus of the optimal incident pressure; (c) the blue solid line represents | p (3.2,y)| in (a); the red dot-dashed line shows | p (3.2,y)| when the wave focus only at ( 3.2,0.9) , which is same as the blue solid line in Fig.3(c); and the black dashed line shows | p (3.2,y)| when the wave focus only at ( 3.2,0.1).The frequency and geometries of the waveguide are same as Fig.3.

圖5 含散射體剛硬波導示意圖Fig.5.Configuration of rigid waveguides involving a scatterer.

然后將方程(18)變換為模態展開系數 pn(x) 滿足的模態域方程[20]:

(19)式中K與(10)式中一致, E和F的表達式為

其中

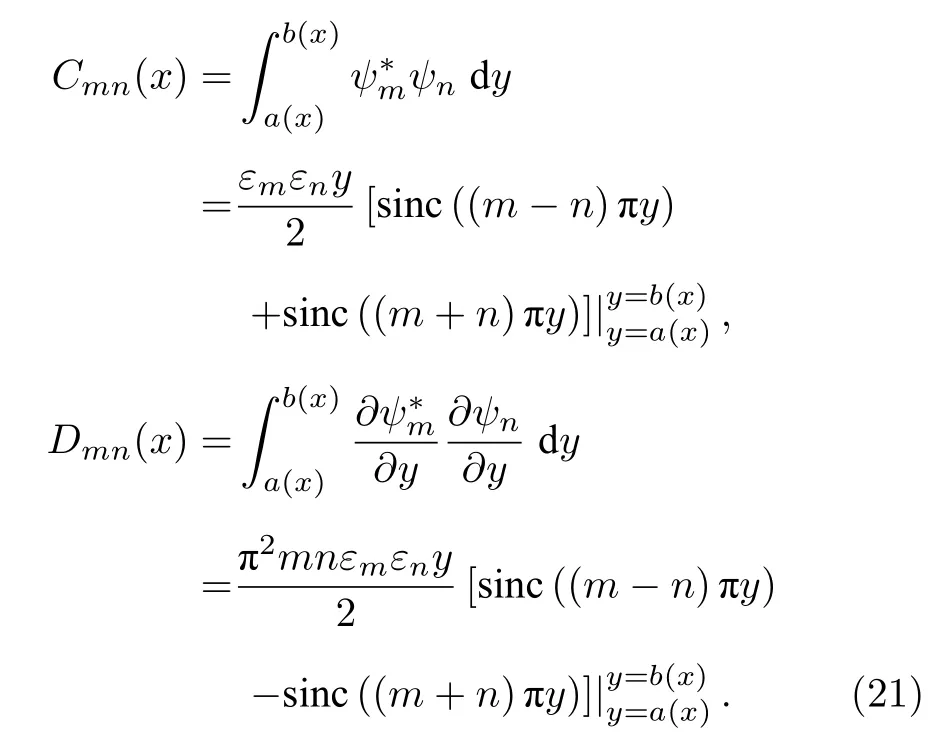
令 s =E?p/?x=Yp , (19)式可寫成耦合偏微分方程組形式:

此時導納矩陣Y與傳播算子M滿足的方程和初條件分別為

二者依然可利用四階Magnus積分格式進行數值求解[24,25].同樣地, 依照 (13)—(16)式, 可計算得到含散射體波導內任意位置處產生聲聚焦的最佳入射聲壓.

圖6 (a) 含散射體波導中的聚焦聲場, 聚焦點位于 ( 3,0.35) ; (b) pi= Λψ0(y) (平面波) 入射時的聲場; (c) 產生 (a)中聲聚焦的最佳入射波(藍色實線)與入射平面波(黑色點線)的幅值分布; (d) 藍色實線與黑色點線分別為(a)與(b)中 x =3 處的聲壓幅值分布Fig.6.(a) Sound focusing field in the waveguide with a scatterer.The focus is located at ( 3,0.35) ; (b) sound field generated by a plane wave pi= Λψ0(y) ; (c) modulus of the pressure of optimal incident wave in (a) and that of the plane incident wave in (b);(d) | p (3,y)| in (a) (blue solid line) and (b) (black dotted line).

圖6給出了計算含散射體波導中聲聚焦的算例.圖6(a)為在 ( 3,0.35) 處產生聚焦的聲場(聲壓幅值分布), 輸入的入射波是由(16)式計算得到的最佳入射波(圖6(c)中藍色實線), 圖6(b)是平面波(圖6(c)中黑色點線)入射時的聲場.圖6(d)中的藍色實線為圖6(a)中聲場在 x =3 處的聲壓幅值分布, 黑色點線對應圖6(b)在 x =3 處的聲壓幅值分布.入射波頻率均為 k =29.1π , 散射體為圓形, 圓心位于 ( 1.6,0.45) , 半徑為 0.3.散射體的介質參 數 設 為 ρ1/ρ2=0.01 , η =?0.99 ( c1/c2=0.01 ),近似剛硬, 因此散射體近似看作對聲波僅有反射作用.可以看出, 剛硬散射體的尺寸較大, 對聲波有強烈的反向散射作用, 但是當輸入計算得到的最佳入射波時, 聲波利用散射體的散射和邊界的反射作用, 仍然可在目標點處發生聚焦.

3.3 聲速垂直變化波導中的聲聚焦

考慮波導中介質參數隨空間位置連續變化的非均勻情況, 對應的典型波導為淺海波導, 表現為聲速沿垂直方向的連續變化, 且海面為軟邊界.此時聲壓滿足的亥姆霍茲方程及邊界條件為

對聲場解進行模態展開, 令

其 中 ψn(y) 變 為將展開式代入(24)式并投影到局部本征函數利用正交性, 可得入射聲壓在任意點(x0,y0)處產生的聲壓為

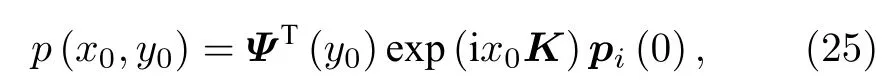
其中 pi(0) 為入射聲壓 pi的模態展開系數, K的表達式為

其計算方法參照文獻[27].由(25)式可知, 在(x0,y0)產生聲聚焦的最佳入射波的模態展開系數為

由于聲速垂直變化波導在傳播方向上介質參數不變, 聲聚焦現象與均勻波導中的聚焦現象類似, 這里不再贅述.

接下來考慮在聲速垂直變化及散射體共同作用下的復雜波導聲聚焦問題, 模型類似圖5, 其中聲速 c1(y) 與 c2(y) 變為y的函數.此時聲壓滿足的亥姆霍茲方程為

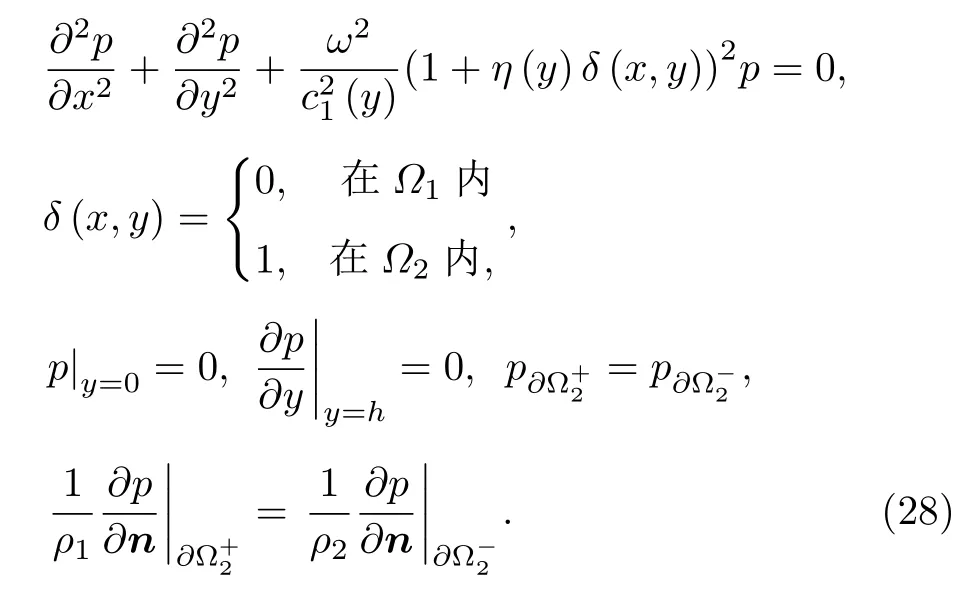
對(28)式的求解依然基于多模態導納法, 詳細的方程推導, 映射算子 M (x) 及透射矩陣T的構建和計算見文獻[27].利用映射算子及透射矩陣, 參照(13)—(15)式的分析過程, 構建任意點 ( x0,y0) 處聲壓與入射聲壓的模態展開系數 pi(0) 的映射關系,其中矩陣K的表達式由(26)式給出.最后根據(16)式計算產生聲聚焦的最佳入射條件.

圖7(a)給出利用上述方法計算的淺海波導中同時存在聲速垂直變化和散射體時的聚焦聲場, 聚焦點位于 ( 35h,0.1h) , 對應最佳入射波幅值分布見圖7(c)插圖.入射波頻率為 f = ω/2π=200Hz , 波導深度 h =100m , [散射體成山狀, 邊]界表達式為a(x)=h?0.5hexp?(x?20h)2/18h2, b (x)=h ,范圍為 [ 8 h,32h].海水介質密度 ρ1=1000kg/m3, 聲速為典型淺海負聲速梯度 c1=1530?0.1y(m/s)[28],如圖7(b)所示, 散射體介質的密度和聲速為ρ2=2ρ1及 c2=2c1(或 η =?0.5 ).圖7(c)給出了圖7(a)中聲場在 x =35h 處的聲壓幅值隨深度的變化曲線(藍色實線), 并與輸入第一階展開模態pi= Λψ0(y)(圖7(c)插 圖 內 黑 色 虛 線)時 在x=35h處獲得的聲壓(黑色虛線)作對比, 此時聲能流的歸一化系數L由(29)式計算:

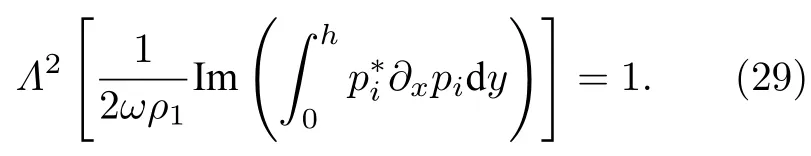
在負聲速梯度的作用下, 聲波在傳播時會向海底彎曲, 并且由于海底山狀散射體的反向散射作用, 部分聲能會被限制在 x ∈[0,20h]區域, 而選擇的聚焦點 ( 35h,0.1h) 既位于透射區域, 又處在海面附近,直覺上聲波似乎難以傳播至聚焦點所在區域, 但輸入計算得到的對應目標點的最佳入射波時, 實現了在該點良好的聲聚焦現象.由于散射體不再近似剛硬, 在圖7(a)中可以發現散射體內部存在聲壓分布, 且密度和聲速的不同改變了聲波的波長.最佳入射聲波在實現聚焦的傳播過程中充分地利用了邊界的反射、散射體的散射以及聲速梯度變化引起的介質折射率變化等因素, 最終在目標點處獲得了最大聲壓.

圖7 (a) 負聲速梯度含散射體淺海波導中的聲聚焦, 波導深度 h =100m , 聚焦點 ( 35h,0.1h) 位于透射區域; (b) 聲速垂直變化情況; (c) x =35h 處聲壓幅值隨深度的變化曲線(藍色實線)以及 pi= Λψ0(y) (非平面波)入射時產生的聲壓(黑色虛線)對比,插圖中為最佳入射波及 pi= Λψ0(y) 的幅值分布Fig.7.(a) Sound focusing field in the waveguide with negative sound-speed gradient and a scatterer.The focus is located at(35h,0.1h), where h =100m is the depth; (b)the sound speed profile; (c) | p (35h,y)| (blue solid line) compared with that generated by pi= Λψ0(y).The insetplotsthe modulus of the optimal incident pressure (blue solid line) and Λ ψ0(y) (black dashed line).

4 討 論

基于多模態導納法, 本文提出在非均勻波導中的任意位置處實現聲聚焦的理論分析方法.多模態導納法可以簡單直觀地將亥姆霍茲方程變換為模態域的耦合偏微分方程組, 并能夠有效地規避數值積分時衰逝模態可能帶來的指數發散問題, 是一種準確高效求解非均勻波導聲場的手段.

由于實際中難以把計算得到的精確最佳入射波作為輸入, 故討論當稀疏輸入最佳入射波時的聲聚焦效果.以圖3(a)中變截面波導的聲聚焦為例,分別以半波長和單倍波長為間隔對理論得到的最佳入射波(圖3(c))進行空間采樣, 獲得稀疏入射波(圖8(c)).通過數值積分及適當補零得到對應的模態展開系數, 進而計算聲場, 結果分別對應圖8(a)及圖8(b).兩個聲場在聚焦點 x0=3.2 處的幅值分布在圖8(d)中給出, 并與理論值進行對比.由圖8可知, 半波長離散得到的稀疏輸入產生的聚焦效果與理論情況基本一致, 原因是半波長離散后的輸入可包含絕大部分原輸入聲波的信息(奈奎斯特采樣定律), 從而能夠產生良好的聚焦效果.而以單倍波長離散得到的稀疏輸入作為聲源時, 該聲源只能包含理論最佳入射波的部分信息, 故產生的聚焦效果對比理論情況有所下降, 但依然可觀察到明顯的聚焦現象.因此, 在y方向稀疏輸入最佳入射波時,通過合理的離散, 仍可實現良好的聲聚焦效果.

此外, 考慮當最佳入射波的幅值或相位存在誤差時對聲聚焦效果產生的影響.依然以圖3(a)為例, 首先固定最佳入射波的相位, 構造一個關于y的取值在 [ 0.5,1.5]均勻分布的隨機函數, 將其與最佳入射波的幅度相乘(相當于對最佳入射波的幅度疊加了一個上限為 ± 50% 的隨機偏差)作為輸入(圖9(c)紅色虛線), 進而求解聲場 (圖9(a)).接著,固定最佳入射波的幅值, 類似地, 構造一個在[?π/2,π/2]區間內均勻分布的隨機函數疊加到最佳入射波的相位上作為輸入(圖9(c)黑色點劃線)并求解聲場(圖9(b)).兩個聲場在聚焦點 x0=3.2 處的幅值分布在圖9(d)中給出, 并與無擾動時的理論值對比.從圖9(a)和圖9(d)可以看出, 當最佳入射波的幅值存在較大范圍隨機擾動時, 其產生的聚焦效果與理論情況基本一致.而根據圖9(b)和圖9(d), 當最佳入射波的相位存在隨機擾動時, 聚焦效果有所下降.聲源存在隨機擾動時依然可產生聚焦的原因是波導中的衰逝模態能夠抑制聲波高階振蕩(與波長對比)成分的傳播, 所以即便入射聲波的幅值或相位存在隨機誤差, 經過衰逝模態的修正, 擾動后的入射波依然會在目標位置處實現聲聚焦效應.圖9表明聲聚焦對幅度的擾動具有強魯棒性, 對相位的擾動兼具一定的穩健性.

圖8 y方向稀疏輸入對聚焦結果的影響 (a) 對最佳入射波進行半波長采樣后的聚焦聲場;(b) 對最佳入射波進行單倍波長采樣后的聚焦聲場;(c)采樣后的入射波幅值分布; (d) 聚焦點 x0 處的聲壓幅值分布.藍色實線為理論值, 與圖3(c)中的藍色曲線一致Fig.8.Sound focusing fields when the optimal incident wave is discretized: (a) Half-wavelength spacing; (b) single-wavelength spacing; (c) the moduli of the two spaced incident waves; (d) the red dashed line and the black dot-dashed line are the corresponding|p(3.2,y)| generated by the incident waves in (c).The blue solid line is the theoretical result which is same as that in Fig.3(c).

圖9 (a) 最佳入射波的幅值存在隨機擾動時的聚焦聲場; (b) 最佳入射波的相位存在隨機擾動時的聚焦聲場; (c) 紅色虛線與黑色點劃線分別為幅值擾動與相位擾動后的入射波幅值分布; (d) 紅色虛線與黑色點劃線分別為(c)中的入射波在聚焦點 x0 處產生的聲壓幅值分布, 藍色實線為理論值, 與圖3(c)中的藍色曲線一致Fig.9.Sound focusing fields when (a) the moduli and (b) the arguments of the optimal incident wave are perturbed; (c) the red dashed line is the incident wave with perturbed moduli, and the black dot-dashed line is that with perturbed arguments; (d) the red dashed line and the black dot-dashed line are the corresponding | p (3.2,y)| generated by the incident waves in (c).The blue solid line is the result without perturbation which is same as that in Fig.3(c).

另外, 本文實現的聲波空間聚焦是輸入最佳入射條件時, 相應位置處聲壓的幅值達到最大.最佳入射條件通過推導聲壓場與入射波的映射關系, 即映射向量 QT(x0,y0) 給出, 該映射關系在透射區域用透射矩陣描述, 在散射區域由傳播算子表征.在光學領域, 有很多學者研究優化透射理論(optimal wave transmission), 對透射矩陣進行處理, 實現波的最大能量透射[29,30].本文的方法結合優化透射理論, 可以為實現非均勻波導中全透射聚焦提供可行性, 使波既能全透射(無反射)地穿過散射區域, 又能產生空間聚焦.

5 結 論

本文分析了水平變截面、含散射體以及聲速垂直變化三種非均勻波導中的聲聚焦現象, 叢理論上推導出使聲波在波導中任意位置處聚焦的入射條件.采用多模態導納法, 將聲壓及其水平方向偏導數用(局部)本征模態作為基底展開, 代入亥姆霍茲方程中進行投影, 利用本征模態的正交性, 最終使聲壓滿足的亥姆霍茲方程轉化為模態展開系數的耦合偏微分方程組.引入導納矩陣和傳播算子,計算反射矩陣和透射矩陣, 給出任意一點處聲壓與入射聲壓的映射關系, 將聚焦問題轉變為級數求和或希爾伯特空間內積的極值問題, 發生聚焦時的入射波模態展開系數為映射向量的共軛轉置.結果表明, 當入射聲波是計算得到的精確的最佳入射聲波時, 可在均勻、非均勻波導中實現明顯的單點或多點聲波聚焦現象.并且當稀疏輸入最佳入射波, 或最佳入射波的幅度或相位存在誤差時, 仍可實現較好的聲聚焦效果.聲聚焦對幅度的擾動具有強魯棒性, 對相位的擾動有一定的穩健性.聲聚焦的過程充分利用了波導的結構及非均勻性對聲波的散射作用, 例如邊界的反射、散射體或邊界起伏帶來的前向后向散射以及聲速梯度變化引起的介質折射率連續變化等.該方法在聲保密通信、超聲醫療及無損檢測等領域具有潛在的應用價值.