基于線性規劃的水資源優化配置

張志鵬

（河海大學水利水電學院，江蘇 南京 210098）

0 引言

水資源是人類社會發展進步的物質基礎，也是生態系統維持穩定的基石[1]。隨著城市化的快速發展，城市水資源供需矛盾日益加劇，水資源優化配置方面的相關研究顯得尤為必要[2]。對水資源配置的優化是將水資源的空間存儲位置和分配規則進行調整，提高水資源整體的利用效率和經濟效益[3]。

針對水資源的優化配置模型，國內外許多學者都進行了一定的研究。水資源配置問題在20 世紀40 年代就被提出，最開始被應用于解決水資源供需矛盾[4]。在之后的研究過程中線性規劃、動態規劃和多目標規劃不斷得到應用，豐富了水資源優化配置的理論。Afza 等[5]針對巴基斯坦某地區的灌溉系統建立了線性規劃模型,并驗證了模型的準確性,指出通過該模型進行的水資源分配可較傳統方法所需水量大幅度降低。婁帥等[6]在漳河流域建立水資源優化配置的免疫遺傳算法模型,最終確定了最優水資源配置方法。佟婧芬[7]基于動態規劃算法對水資源優化配置進行研究，得出動態規劃算法在水資源優化配置中應用較好,可為同類地區水資源配置方案設計提供參考借鑒。基于上述學者的研究，本文借助線性規劃模型對現有的供水問題實例進行求解分析。

1 水資源優化配置的涵義

水資源的優化配置，包括兩方面的涵義：一方面，在水資源短缺的區域，是指對各行業、各部門之間進行合理的用水分配，使用水達到區域效益最高，從而保證區域協調、健康的發展；另一方面，在水資源豐富的區域，是指對本區域內的產業結構進行宏觀調控，以充分提高各行業、各部門對水資源的利用效率。以上兩個方面，是水資源優化配置作為保障水資源可持續利用的重要內容。

在水資源的系統分析中，要實現用有限的水資源最大限度的滿足各用水部門的需求，使各用水部門取得最好的經濟效益、社會效益和環境效益。這從數學觀點而言，就是指在滿足各種約束條件下，對水資源系統數學模型中的目標函數進行最優化處理（求最值的方法），如果這里的目標函數和所有的約束條件都是線性的，這種最優化問題就是線性最優化，即水資源系統線性規劃，常用數學中的線性規劃法求解。

2 線性規劃方法

2.1 線性規劃簡介

線性規劃是運籌學中研究較早、發展較快、方法較成熟和應用最廣泛的一個分支，它是研究如何合理調配和有效使用現有的人力、物力等資源，以達到最優目標（多、快、好、省）的一種數學方法。因此，線性規劃就是求一組變量（決策變量）的值，使它們滿足一組線性等式或不等式的限制條件（約束條件），并使一個線性函數（目標函數）的值最大（或最小）的方法。線性規劃建模簡單，并且有通用的算法（單純形法）和計算機軟件進行計算，因此這種方法已廣泛應用于資源分配、投資組合、交通運輸、生產管理、軍事通訊和營養調配等眾多領域。

2.2 線性規劃模型

線性規劃模型的特征是：（1）有一組決策變量；（2）有一組線性約束條件，它們是線性等式或不等式；（3）有一個確定的目標，這個目標可以表示成決策變量的線性函數，根據問題的不同，有的需求最大值，有的需求最小值。由此可見，一個線性規劃問題的數學模型，必須含有三個要素：決策變量、約束條件和目標函數。

因此，建立線性規劃模型的步驟為：

（1）根據所要達到的目的找到決策變量，并用數學符號表示它們；

（2）由決策變量所受的限制條件，確定決策變量所要滿足的約束條件（線性方程或線性不等式）；

（3）根據所要達到的目的和決策變量，列出關于決策變量的線性目標函數。

線性規劃的數學模型可表示如下：

求解線性規劃問題的方法有圖解法和單純形法，單純形法是求解線性規劃問題的基本方法。

3 線性規劃模型在水資源優化配置中的應用

3.1 利用線性規劃求解輸水費用最小問題

甲、乙兩個水廠向某城市輸送生活、農業和工業用水，甲水廠的月供水量400 萬m3，乙水廠的月供水量780 萬m3，該城市生活用水的月需求量不低于200 萬m3，農業用水的月需求量不低于450 萬m3，工業用水的月需求量不低于400 萬m3。由于各種用水的輸水距離和輸水條件不同，故輸水費用也不同，甲水廠的生活用水的輸水費用為6 千元/萬m3，農業用水的輸水費用為3 千元/萬m3，工業用水的輸水費用為5 千元/萬m3；乙水廠的生活用水的輸水費用為5 千元/萬m3，農業用水的輸水費用為9 千元/萬m3，工業用水的輸水費用為6 千元/萬m3。試設計在滿足各種用水需要的條件下，月輸水費用最小的方案。

為了使問題更加清晰，將上面的水資源優化問題用表格的形式展現，具體內容見表1。

表1 供水信息表

針對上面的月輸水費用最小問題，建立的數學模型如下：

設甲水廠向該城市輸送生活、農業和工業用水的月供水量為x11，x12，x13，乙水廠向該城市輸送生活、農業和工業用水的月供水量為x21，x22，x23，以x11，x12，x13，x21，x22，x23為決策變量。

（1）目標函數的確定

求月輸水費用最小的方案應選月輸水費用最小為目標函數，即minZ=6x11+3x12+5x13+5x21+9x22+6x23。

（2）約束條件的確定

并滿足各種用水的月需水量要求，即：

且各水廠的月供水量應小于或等于水廠的月供水能力，即：

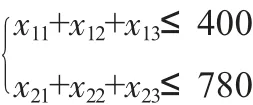
水廠向各區供水量應大于或等于0，即：

使用求解線性規劃問題，得到：

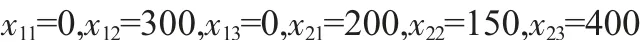
這時候得到輸水費用最小，為5650 元/萬m3。

3.2 利用線性規劃求解供水效益最大問題

某庫區年供水能力為6500 萬m3，其任務是向A、B、C 三農業區灌溉供水，因為庫區距離各農業區的輸水距離不同，庫區對各農業區的輸水條件也不同，所以庫區向不同的農業區供水的成本和價格不一樣，故供水的利潤也不一樣。各農業區的年需水量、供水的水價、水廠的供水成本、最小供水量見表2。試設計最佳供水方案，使得在滿足各農業區需水的條件下，該庫區的供水效益最大。

為了使問題更加清晰，我們將上面的水資源優化問題用表格的形式展現，具體內容見表2。

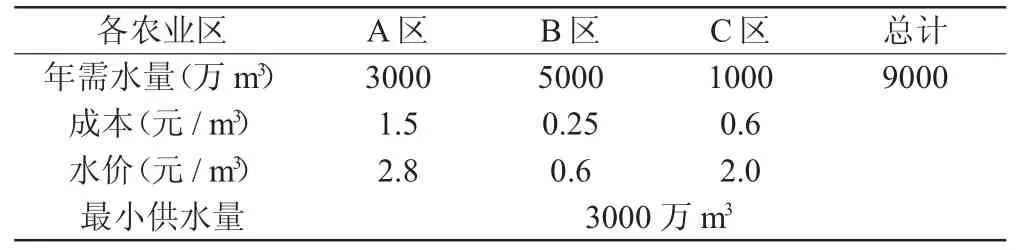
表2 供水信息表

針對上面的月輸水費用最小問題，建立的數學模型如下：

A、B、C 三農業區的年需水量為決策變量，設為x1，x2，x3。

（1）目標函數的確定

根據三農業區的年需水量要求以及水價和成本來確定最優分配方案，可確定供水效益最大為目標函數，即maxZ=（2.8-1.5）x1+（0.6-0.25）x2+（2.0-0.6）x3。

（2）約束條件的確定

三農業區的年總需水量應小于等于水廠年總供水量，即：x1+x2+x3≤6500；

三農業區的最大需水量限制為：x1≤3000；x2≤5000，x3≤1000；

三農業區的最小需水量應大于等于0：x1≥0，x2≥0，x3≥0。

利用Microsoft Excel 規劃求解工具進行求解，可求得供水效益最大為5700 萬元，達到最大效益時，A、B、C 三區的年需水量分別為：x1=2500 萬m3，x2=3000 萬m3，x3=1000 萬m3。

4 結論

（1）通過水資源優化配置的介紹和基于線性規劃模型優化配置水資源實例分析得出：利用線性規劃法處理水資源優化配置問題，建模過程簡單，求解過程容易，能大大的簡化水資源配置問題。

（2）線性規劃模型只能解決較為清晰簡單的目標問題。如果目標函數或約束條件中存在非線性方程或存在多目標間相互矛盾，往往還需要結合非線性規劃法、動態規劃法等方法，存在一定的局限性。

（3）水資源優化配置的基本理論和方法有很多種，但在實際的問題解決上，要選用最適合的方法進行實際問題分析。這樣可以最大限度的實現水資源的優化配置，最大限度的利用有限的水資源。