近58 年馬鞍山市降水量變化規律分析

邢壽文

（安徽省馬鞍山水文水資源局，安徽 馬鞍山 243000）

0 引言

進入21 世紀，全球變暖日益明顯，區域極端天氣災害頻繁[1～3]。暴雨作為一種極端天氣，給城市人民財產和生命帶來了極大的危害，關于暴雨預報、由暴雨引起的洪水災害評估已經成為當下研究的熱點問題[4～5]。馬鞍山是中國東部安徽省的一個地級市。它是一個橫跨長江的城市。馬鞍山河流較多，主要包括揚子江的馬鞍山河段、采石河、玉山河、磁湖河、玉山湖和索溪河，因此水資源較為充沛。受自然地理，氣候，人類活動和工程條件的影響，馬鞍山地區的洪水頻繁發生，暴雨持續時間短，范圍廣，位于該省年平均降水量的高值區域。本文以馬鞍山以及周邊氣象站的月值降水數據為基礎。利用小波分析，對過去58年降水的時間- 周期趨勢進行分析，為該地區防洪減災提供理論參考。

1 資料與方法

1.1 資料來源與數據處理

本文利用馬鞍山及周邊地區四個氣象站的月降水觀測資料（來自中國氣象科學數據共享服務網）。將四個氣象站數據進行平均處理，代表馬鞍山的年平均降水量。分析了地區降水的時空變化特征，研究期為1961 年～2018 年。從統計學角度說，相對長的時間序列能夠保證研究區域分析結果的可靠性。

1.2 研究方法

本研究采用趨勢分析法、Mann-Kendall 檢驗法以及小波分析法對馬鞍山降水變化趨勢以及規律進行分析。為分析徑流量的變化趨勢，本文采用傾向率方法進行分析，即建立徑流量與時間的一元線性回歸方程，來反映徑流量的變化趨勢。本文以近58 a 的降水數據為基礎，對其進行非參數檢驗，以反映馬鞍山降水的變化趨勢。最后通過小波分析對研究區內降水周期變化進行研究。

（1）Mann-Kendall 檢測法

Mann-Kendall 檢驗法是一種非參數統計檢驗方法，用于預測各種觀測要素的時間序列數據的長期趨勢。Mann-Kendall 檢驗中，原假設H0為原序列(x1，x2，…，xn)無變化趨勢，備擇假設H1為雙邊檢驗，構造秩序列Sk：

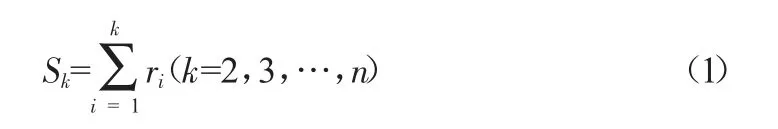
式中：

定義統計變量：

UFk為標準正態分布，對于給定顯著性水平α，若UFk>Uα/2，則表明原序列存在明顯的趨勢變化。將時間序列逆序排列為xn，重復相同的操作，得到UBk，滿足UBk=-UFk（k=1,2,…,n）。通過UFk和UBk的曲線走勢可分析序列x 的變化趨勢。當兩條曲線相交，則為突變時刻。

（2）小波分析法

針對水文數據的特征，本文選用Morlet 小波作為小波函數φ(t)，時間序列f(t)的小波變換為：

其中：Wf(a,b)稱為小波變換或小波系數（t）為復共軛函數；a>0 為尺度因子，反映了小波周期長度；b 為時間因子，反映了在時間上的平移。Wf(a,b)反隨a 和b 變化，可做a 為橫坐標、b為縱坐標的等值線圖。此圖可反映隨時間變化的小波特征。不同時間尺度下的小波系數可以反映系統在該周期下的變化特征。φ（t）可以取不同形式，Morlet 小波的變換形式為：

小波方差由下式表示，可用來確定主周期：

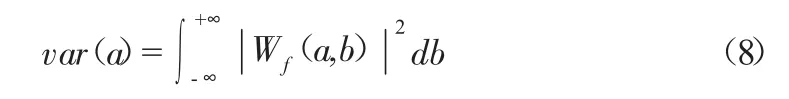
2 降水量時間變化特征分析

2.1 年降水量變化分析

圖1 馬鞍山近58 年降水量變化趨勢

馬鞍山多年平均降水量為1139 mm，且整體處于上升趨勢，降水變化傾向率為3.6373 mm/a，由于季風的影響，該地區的降水量在年內和年際變化很大，這使得該區域經常有集中的大雨和交替的干旱和洪水。6 月份以后，進入東南季風控制時期，暴雨由南向北逐漸增多，7 月～8 月份是頻發時期，占暴雨次數的63%～68%，這是7 月份最多，占38%～45%，并在9 月中旬后逐漸減少，最后在10 月份逐漸減少。暴雨持續日數，一般為1 天～2 天，最長3 天。暴雨與洪水密切相關，暴雨的強度和總量決定了洪水的嚴重程度。該地區的暴雨持續時間短，強度大，范圍廣，是安徽省年平均降水量的高值區域。

2.2 降水量季節變化特征分析

表1 降水季節變化特征

由于處于亞熱帶季風氣候區，夏季受來自海洋的暖濕夏季風影響，降水明顯增多，流域內降水季節性變化明顯。由表1 可知，降水主要集中在夏季，平均降水量為688.0 mm，占年降水量的60.4%。其次是春季和秋季，降水量分別為184.5 mm 和203.9 mm，占年降水量的16.2%。17.9%，而冬季降水量僅為61.5 mm，約占年降水量的5.4%。從降水變化率來看，春、秋季降水變化率為負值，分別為-3.7 mm/10 a 和-3.1 mm/10 a，夏、冬季降水變化率為正值，分別為2.4 mm/10 a、和0.4 mm/10 a。

2.3 年降水量M-K 檢驗

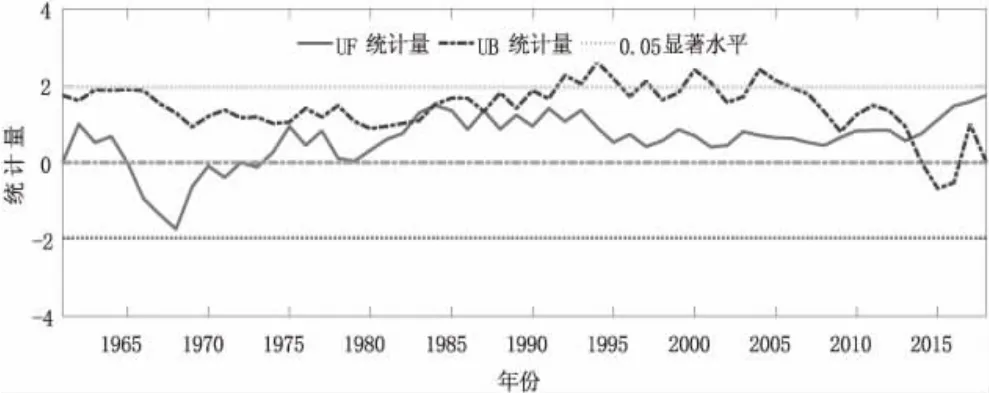
圖2 馬鞍山近58 年降水量突變檢驗

圖2 為馬鞍山降水量突變檢驗圖，從圖中可以看出，在研究時間范圍內有多個突變點，主要發生在1975 年、1982 年、1984 年、1987 年和2014 年左右，且都在0.05 置信區間范圍以內，說明降水量振蕩變化明顯，尤其是在20 世紀80 年代發生多次突變，振蕩最為強烈，到90 年代降水量整體呈現減少趨勢，然后維持在一個水平，在2010 年以后開始大幅增長。

3 降水量時間周期分析

為了進一步研究地區年降水量的時間推移趨勢，對馬鞍山近58年的降水進行了小波分析。采用MATLAB 進行繪制，結果見圖3～圖6。

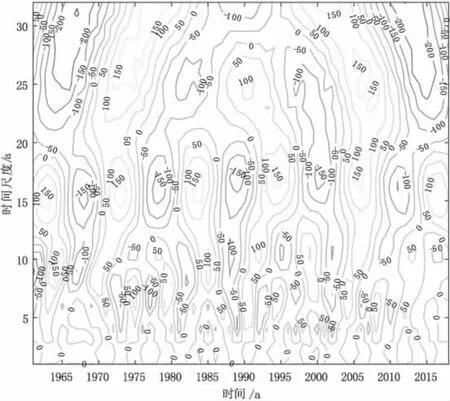
圖3 馬鞍山年降水量小波實部等值線圖

選定的數據是由年平均降水量（1961 年～2018 年）表示的平面，其中，橫坐標為時間，縱坐標為時間尺度，圖中的等值曲線為小波系數實部值。當小波系數實部值為正時，代表降水量的豐水期；為負時，表示降水量的枯水期。因此小波變換系數的實部在平面輪廓上的正負值是在時域上反映了降水降水量的枯豐交替的變化，反過來，可以判斷不同時間尺度的年降水量的未來趨勢[3]。

從圖3 中，我們可以清楚地看到58 a 年降水量演變中存在的多時間尺度特征。不同尺度的正相和負相之間振蕩中心的形成具有明顯的年際和年代際變化。總的來說，在降水演變過程中，有三種類型的周期性變化模式，分別為3 a～8 a，13 a～20 a和22 a～32 a。其中，年降水量有兩個準振蕩周期，在22 a～32 a范圍內。1984 年～1995 年及2006 年以后為枯水年，1973 年～1983 年及1996 年～2005 年為豐水年。13 a～20 a 的年際變化尺度存在枯豐交替5 次周期振蕩，周期連續性最為完整；3 a～8 a 的年際變化尺度沒有全局性。

圖4 模等值線圖

圖5 模方等值線圖

從小波變換系數模值和模值的平方等值線圖可以看出（圖4 和圖5），地區22 a～32 a 尺度的周期變化最為明顯。但其周期性變化具有局部化特征，不具有全域性，從圖中可以看出此時間尺度在兩端時間區域內周期性較強，其他時間段較弱，能量較低，能量先趨向下降然后隨時間增加。其次，13 a～20 a尺度的周期變化也很明顯，具有全球性。時間尺度3 a～8 a具有最差的周期性，弱能量和不均勻分布，也沒有全局性。在3 a～8 a 尺度中模值最高值出現在1973 a～2010 a，此時段周期性較強，能量值與其他時間段相比也最大。

圖6 小波方差圖

小波方差圖可以用時間尺度反映降水時間序列的波動能量分布，小波方差隨尺度的變化而變化。該過程可以反映時間序列中包含的各種尺度（周期）的特征以及它們作為比例函數的優缺點（能量大小）。因此，通過小波方差圖（即降水過程中存在的主要周期）找到時間序列中的主要尺度（周期）非常方便。

研究區域降水的小波方差圖有兩個不同的峰值（圖6），分別對應于26 年和16 年的時間尺度，并且在整個研究時間范圍內可測量時標的最大值對應于32 年時標。因此馬鞍山年降水量變化的第一個主要周期為32 年；26 年的時間尺度對應于第二個峰值，這是降水量變化的第二個主要時期。這表明上述三個周期的波動決定了整個時域降水量的變化特征。

4 結論

（1）受季風影響，馬鞍山年內降水量變化較大。處于安徽省多年平均降水量的高值區，6 月份以后，進入東南季風控制時期，暴雨由南向北逐漸增多，7 至8 月份是頻發時期，占暴雨次數的63%～68%，9 月中旬后逐漸減少。

（2）馬鞍山春、秋季平均降水變化率為負，夏、冬季平均降水變化率為正。分別為-3.7 mm/10 a、-3.1 mm/10 a，2.4 mm/10 a和0.4 mm/10 a，降水變化趨勢在不同季節有很大差異，整體呈增長趨勢。

（3）馬鞍山降水演變中有3 a～8 a，13 a～20 a 和22 a～32 a三種周期性變化。其中22 a～32 a 尺度的周期變化最明顯。13 a～20 a 的周期性變化是第二個，3 a～8 a 尺度的周期性最差，能量較弱，分布不均勻；馬鞍山降水量分別存在32 a、26 a、16 a這3 個時間尺度周期，其中32 a 是該地區年降水量變化的第一個主要時期；26 a 和16 a 分別為降水變化的第二和三主周期；方差的三個峰值都在3 類時間尺度范圍內，也說明了小波變換分析的準確性。