帶有交易成本的均值-方差-下半方差投資組合模型

王曉琴, 高岳林,2,

(1- 北方民族大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院，銀川 750021;2- 寧夏智能信息與大數(shù)據(jù)處理重點(diǎn)實(shí)驗(yàn)室，銀川 750021)

1 引言

為了迎接金融市場(chǎng)的新挑戰(zhàn)，許多學(xué)者和投資者在Markowitz 的理論基礎(chǔ)上發(fā)展了現(xiàn)代投資組合理論.在現(xiàn)代金融學(xué)理論中，投資組合優(yōu)化問(wèn)題就是研究理性的投資者怎樣將自己的資金分配到幾種不同的資產(chǎn)上以期獲得最大可能收益的同時(shí)能承受盡可能小的風(fēng)險(xiǎn).然而，經(jīng)典的Markowitz 投資組合管理模型往往忽略了金融市場(chǎng)上一些實(shí)際存在的摩擦因素，如交易成本的考慮等.在現(xiàn)實(shí)中，無(wú)論是買(mǎi)入還是賣(mài)出證券都需要支付交易費(fèi)用，忽略交易成本往往會(huì)導(dǎo)致無(wú)效的資產(chǎn)組合.因此，王春峰等[1]在投資組合管理模型的基礎(chǔ)上引入了典型的交易成本并進(jìn)行了實(shí)證分析，結(jié)果表明考慮交易成本的投資組合所獲得的收益要小于不考慮交易成本的投資組合所獲得的收益.康志林[2]考慮到交易費(fèi)用對(duì)投資者的投資績(jī)效具有直接影響，因此，在文中考慮了交易費(fèi)用、投資比例的上界以及不允許賣(mài)空等約束的情形.任大源等[3]運(yùn)用凸規(guī)劃相關(guān)理論與Kuhn-Tucker 條件求解了同時(shí)含有交易成本和機(jī)會(huì)成本的投資組合選擇模型.房成德等[4]以條件風(fēng)險(xiǎn)價(jià)值(CVaR)作為對(duì)風(fēng)險(xiǎn)度量的同時(shí)考慮了交易費(fèi)用.Fu 等[5]考慮了在均值方差投資組合模型同時(shí)含有風(fēng)險(xiǎn)資產(chǎn)和無(wú)風(fēng)險(xiǎn)資產(chǎn)，且把整個(gè)投資過(guò)程劃分為兩個(gè)階段.Mansini 等[6]在本文中考慮了帶有線性交易成本的投資組合模型，文中所考慮的模型是一個(gè)混合整數(shù)規(guī)劃模型.Najafi 和Mushakhian[7]在文中考慮了交易成本，并且用方差和條件風(fēng)險(xiǎn)價(jià)值的線性加權(quán)來(lái)度量投資組合的風(fēng)險(xiǎn).Yue 等[8]用進(jìn)化算法求解了考慮交易成本和流動(dòng)性的雙目標(biāo)投資組合優(yōu)化模型.王婧等[9]運(yùn)用蟻群算法解決了股票投資組合優(yōu)化問(wèn)題.李繼和高岳林[10]用均值衡量投資組合的收益，用風(fēng)險(xiǎn)價(jià)值(VaR)度量投資組合的風(fēng)險(xiǎn)并用改進(jìn)后的差分進(jìn)化算法求解了投資組合選擇問(wèn)題.畢曉君和王佳薈[11]把教與學(xué)算法和差分進(jìn)化算法進(jìn)行了融合，以解決算法容易陷入局部最優(yōu)的問(wèn)題.目前，投資組合中風(fēng)險(xiǎn)的度量方法已有好幾種，如：方差、下半方差、絕對(duì)偏差，風(fēng)險(xiǎn)價(jià)值(VaR)和條件風(fēng)險(xiǎn)價(jià)值(CVaR)以及他們之間的一個(gè)加權(quán)組合等等都用來(lái)度量投資組合的風(fēng)險(xiǎn).本文用方差和下半方差的加權(quán)組合來(lái)度量投資所帶來(lái)的風(fēng)險(xiǎn).因此，建立了帶有交易成本的均值-方差-下半方差投資組合模型，并運(yùn)用教與學(xué)算法對(duì)提出的模型進(jìn)行了求解.本文內(nèi)容安排如下：第1 節(jié)給出了考慮交易成本的均值-方差-下半方差投資組合模型；第2 節(jié)給出了求解模型的教與學(xué)算法設(shè)計(jì)；第3 節(jié)給出了實(shí)證分析；第4 節(jié)給出了本文的結(jié)論.

2 考慮交易成本的均值-方差-下半方差投資組合模型

2.1 目標(biāo)函數(shù)

本文只考慮證券市場(chǎng)上存在的n種風(fēng)險(xiǎn)資產(chǎn).

x= (x1,x2,···,xn): 其中xi表示第i種資產(chǎn)的投資比例；ui: 表示第i種資產(chǎn)投資比例的上界；Ci: 表示組合中第i個(gè)風(fēng)險(xiǎn)資產(chǎn)在[0,T]時(shí)間內(nèi)的交易費(fèi)率；Ri: 表示組合中第i個(gè)風(fēng)險(xiǎn)資產(chǎn)在[0,T]時(shí)間內(nèi)的收益率；Rit: 表示第i個(gè)風(fēng)險(xiǎn)資產(chǎn)在第t個(gè)時(shí)期的收益率，其中表示在[0,T]時(shí)間內(nèi)的組合收益率，假設(shè)隨機(jī)變量的期望值可以用歷史收益的均值來(lái)近似表示，即

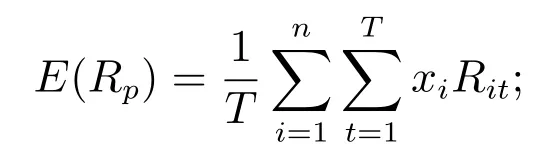
根據(jù)投資組合的理論，目標(biāo)函數(shù)有兩個(gè)：最大化投資組合的收益，最小化投資組合的風(fēng)險(xiǎn)

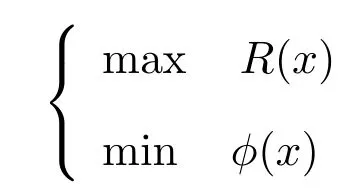
2.2 模型的建立

1) 均值-方差-下半方差投資組合選擇模型

根據(jù)投資組合理論，投資者偏好收益而厭惡風(fēng)險(xiǎn).因此，一般情況下，投資者總是在一定的預(yù)期收益率下，希望投資組合的風(fēng)險(xiǎn)最小，基于均值-方差-下半方差投資組合選擇模型建立如下

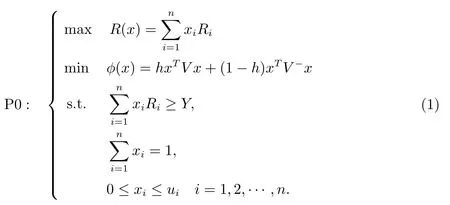
在P0 中，約束條件一表示投資者有某個(gè)能夠接受的最低期望收益率Y；約束條件二表示投資到每一種資產(chǎn)的比例之和為1；第三個(gè)約束條件表示資產(chǎn)不允許賣(mài)空且第i種資產(chǎn)投資比例不超過(guò)ui，則P0 的經(jīng)濟(jì)含義就是在滿足以上三個(gè)約束條件的前提下，怎樣分配資產(chǎn)的投資比例，在風(fēng)險(xiǎn)達(dá)到最小的情況下，使得投資組合獲得最大的收益.

2) 考慮交易成本的均值-方差-下半方差投資組合選擇模型

投資過(guò)程中，交易成本是不能忽略的.在實(shí)際的證券交易中，總存在著交易成本的問(wèn)題，且交易成本對(duì)投資的收益有較大的影響，從而決定投資組合的最終收益.因此，在模型中考慮交易費(fèi)用是非常必要的.這里考慮的交易成本函數(shù)表現(xiàn)為資產(chǎn)交易量具有兩個(gè)拐點(diǎn)的非凸非凹函數(shù)，如圖1 所示，稱之為“典型交易成本函數(shù)”.

BIM技術(shù)具有三維可視化的特點(diǎn)，是對(duì)建筑及構(gòu)件的直觀表達(dá)。所見(jiàn)即所得的方式提高了理解和溝通的效率，降低了二維圖紙閱讀的專業(yè)性要求，對(duì)于復(fù)雜的空間關(guān)系，如復(fù)雜管線、體型復(fù)雜建筑等來(lái)說(shuō)優(yōu)勢(shì)明顯，如圖2所示。

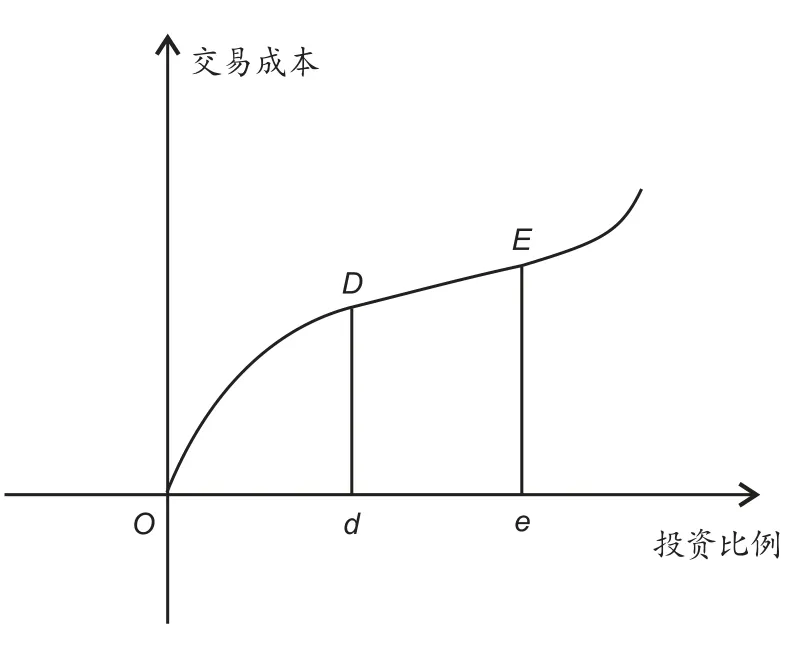
圖1: 交易成本函數(shù)圖

當(dāng)購(gòu)買(mǎi)資產(chǎn)量比較小時(shí)，交易效率較低，所以單位交易成本很大，隨著購(gòu)買(mǎi)資產(chǎn)量的上升，單位交易成本將逐漸減少，故在達(dá)到D點(diǎn)之前，交易成本函數(shù)C(X)是上凸的.然而，當(dāng)越過(guò)D點(diǎn)后單位交易成本已經(jīng)達(dá)到最優(yōu)，所以單位交易成本函數(shù)C(X)基本保持不變，直到到達(dá)E點(diǎn)，也就是說(shuō)DE段交易函數(shù)是線性的.如果購(gòu)買(mǎi)資產(chǎn)量繼續(xù)增加，越過(guò)E點(diǎn)后，由于證券市場(chǎng)上資產(chǎn)供給不足等因素使得對(duì)應(yīng)資產(chǎn)的單位交易成本逐漸變大，所以交易成本函數(shù)C(X)在越過(guò)E點(diǎn)后將變成下凸的.記每次交易時(shí)的成本函數(shù)為C(X)，則成本函數(shù)的表達(dá)式如下[4]

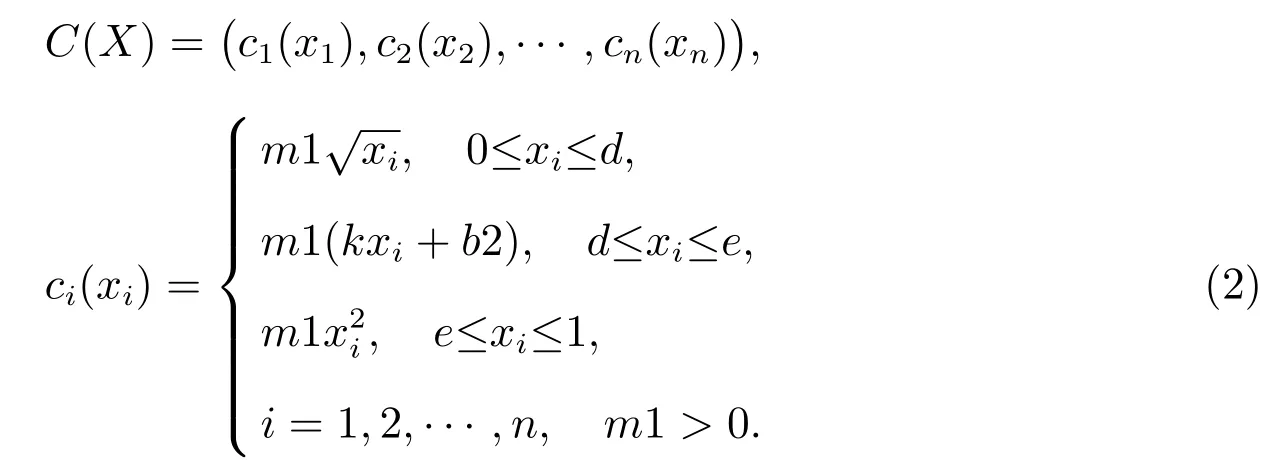
因此，考慮交易成本的均值-方差-下半方差投資組合選擇模型為

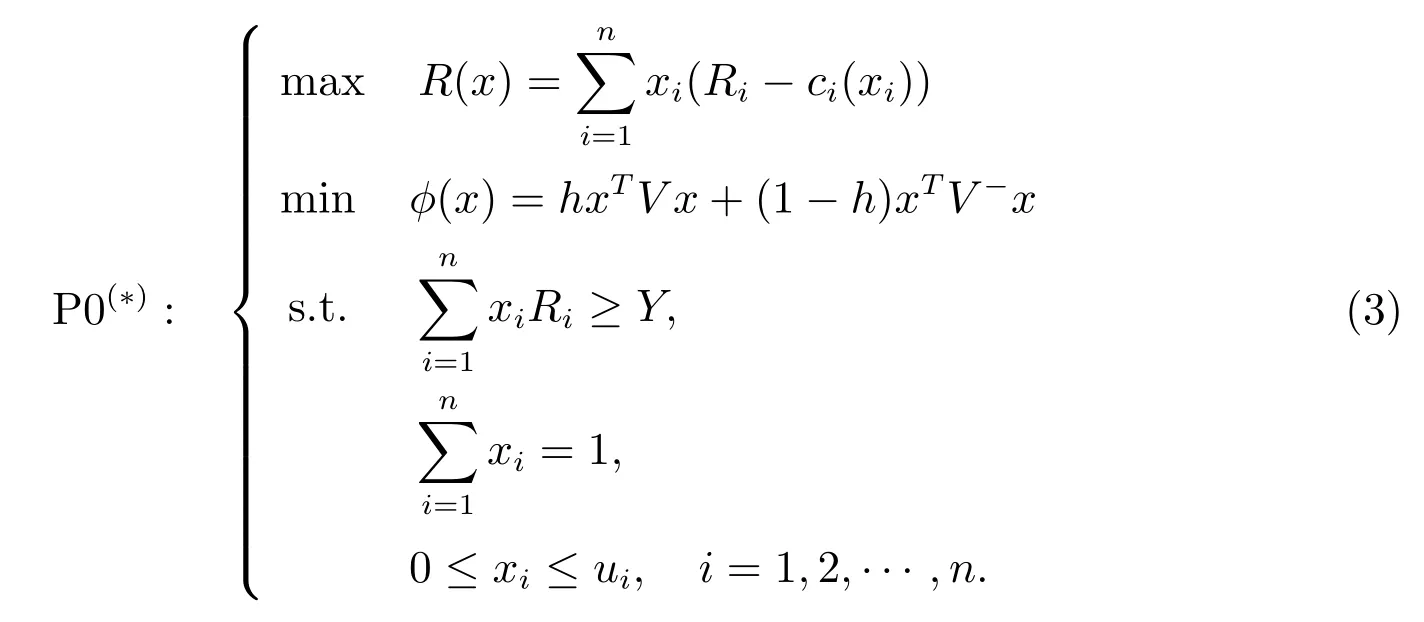
為了更好的實(shí)現(xiàn)風(fēng)險(xiǎn)和收益之間的均衡，考慮同時(shí)優(yōu)化兩個(gè)目標(biāo)，我們引入風(fēng)險(xiǎn)厭惡系數(shù)A(0＜A ＜1)[12]，其中A反映投資者的風(fēng)險(xiǎn)偏好，A值越大，投資者越注重收益.反之，投資者更注重對(duì)風(fēng)險(xiǎn)的控制，轉(zhuǎn)化后的模型如下

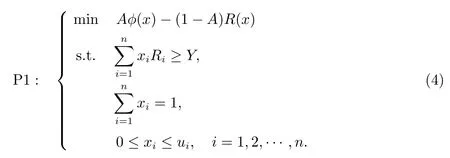
3 求解模型的教與學(xué)算法設(shè)計(jì)

教與學(xué)優(yōu)化算法就是一種以班級(jí)為單位的教學(xué)過(guò)程進(jìn)行仿真模擬的優(yōu)化算法，搜索空間中的每個(gè)種群代表每個(gè)班級(jí)，種群的規(guī)模也就是每個(gè)班級(jí)里的人數(shù)，決策空間的維度就是學(xué)生所要學(xué)習(xí)的科目，每個(gè)學(xué)生的學(xué)習(xí)水平就代表目標(biāo)函數(shù)中的適應(yīng)度值，種群中適應(yīng)度值最好的個(gè)體確定為老師.教與學(xué)優(yōu)化算法主要包括”教師對(duì)學(xué)生的教學(xué)”和”學(xué)生之間的相互學(xué)習(xí)”兩個(gè)階段，通過(guò)這兩個(gè)階段的共同努力來(lái)提升全班同學(xué)的平均水平.

3.1 需要求解的問(wèn)題

本文所建立的是一個(gè)帶有約束的雙目標(biāo)優(yōu)化問(wèn)題，即最大化收益和最小化風(fēng)險(xiǎn)這兩個(gè)目標(biāo).為了簡(jiǎn)化計(jì)算，把雙目標(biāo)的問(wèn)題轉(zhuǎn)化為一個(gè)最小化單目標(biāo)的問(wèn)題，把有約束的優(yōu)化問(wèn)題轉(zhuǎn)化為一個(gè)無(wú)約束的優(yōu)化問(wèn)題.如果計(jì)算所得目標(biāo)函數(shù)值越小，說(shuō)明構(gòu)建的投資組合相對(duì)越好.

3.2 教與學(xué)優(yōu)化算法[13]

a) 教師階段

教師(適應(yīng)度值最優(yōu)的個(gè)體)根據(jù)全班學(xué)生(種群)的平均水平運(yùn)用以下三個(gè)公式對(duì)全班學(xué)生(種群個(gè)體)進(jìn)行教學(xué)過(guò)程：

令i=1:N為種群的規(guī)模

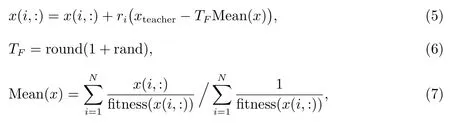
其中ri為[0,1]之間的隨機(jī)數(shù)，xteacher為教師個(gè)體，即當(dāng)前種群的最優(yōu)粒子位置，TF為教學(xué)因子，一般取1 或2.round 表示對(duì)計(jì)算結(jié)果四舍五入取整，rand 取0-1 之間的隨機(jī)數(shù).Mean(x)是班里所有學(xué)生知識(shí)水平的平均值，由公式(7)確定.fitness 表示求適應(yīng)度函數(shù).

b) 學(xué)生階段

學(xué)生在老師進(jìn)行教學(xué)階段之后，為了進(jìn)一步提升自身的水平，與班里的其他學(xué)生按照以下公式進(jìn)行繼續(xù)學(xué)習(xí).

令i=1:N;j=1:N，其中N為種群的規(guī)模，且

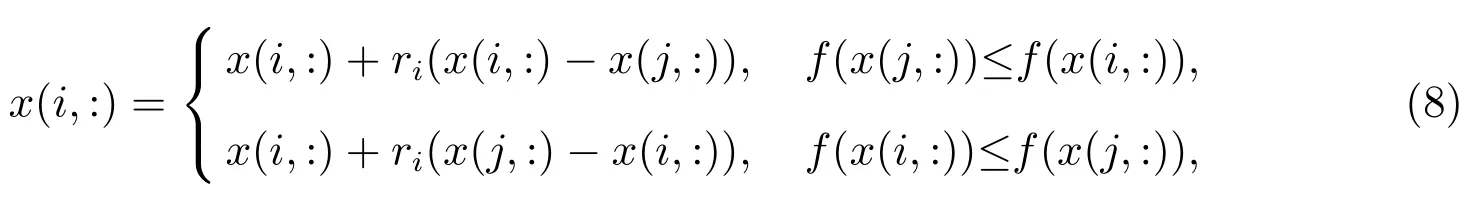
其中x(j,:)為當(dāng)前種群中第j個(gè)粒子的位置，其中f(x(i,:))和f(x(j,:))分別為第i個(gè)粒子和第j個(gè)粒子的適應(yīng)度值.

3.3 教與學(xué)優(yōu)化算法流程

步驟1種群初始化及參數(shù)設(shè)置.包括初始種群的規(guī)模N，最大迭代次數(shù)M，搜索空間維數(shù)D，決策變量范圍(lbi,ubi)以及其他相關(guān)的參數(shù)；

步驟2在搜索空間中初始化每個(gè)學(xué)員，并計(jì)算每個(gè)學(xué)員所學(xué)學(xué)科的綜合成績(jī)(適應(yīng)度值)，把綜合成績(jī)最好(適應(yīng)度值最優(yōu))的學(xué)員確定為xteacher，因?yàn)槲闹兴蟮哪繕?biāo)函數(shù)為最小化的問(wèn)題，所以計(jì)算的適應(yīng)度值越小越好；

步驟3利用公式(7)求班里所有學(xué)員所學(xué)課程成績(jī)的均值Mean(x)，也就是求搜索空間中所有粒子的均值Mean(x)；

步驟4利用公式(5)和(6)執(zhí)行教學(xué)階段，從而對(duì)粒子x(i,:)的位置進(jìn)行更新，并計(jì)算相應(yīng)的適應(yīng)度值；

步驟5利用公式(8)執(zhí)行學(xué)生之間的相互學(xué)習(xí)階段，從而更新粒子位置x(i,:)，并計(jì)算適應(yīng)度值，執(zhí)行選擇操作；

步驟6利用公式(2)計(jì)算每種風(fēng)險(xiǎn)資產(chǎn)的交易成本；

步驟7如果達(dá)到所設(shè)定最大迭代次數(shù)，輸出最優(yōu)解，否則返回步驟2.

4 實(shí)證分析

4.1 模型的轉(zhuǎn)化

運(yùn)用罰函數(shù)法將有約束的單目標(biāo)問(wèn)題轉(zhuǎn)化為無(wú)約束的單目標(biāo)問(wèn)題來(lái)求解，轉(zhuǎn)化以后的等價(jià)模型為

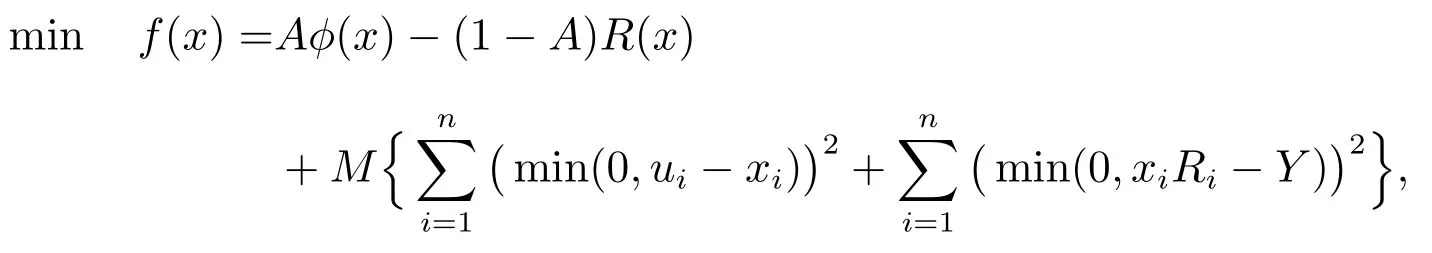
其中M是一個(gè)充分大的正數(shù).

4.2 數(shù)值算例

本節(jié)針對(duì)本文的理論結(jié)果及算法給出了數(shù)值算例.假設(shè)對(duì)表1 中的8 支股票進(jìn)行投資組合，種群規(guī)模N為60，每只股票的投資比例小于等于0.6，交易成本函數(shù)中的m1 = 0.1,a= 0.3,b= 0.4，獨(dú)立運(yùn)行120 次，利用教與學(xué)的Matlab 程序進(jìn)行編碼實(shí)現(xiàn)，得到給定期望收益下的目標(biāo)函數(shù)值、最小風(fēng)險(xiǎn)以及最優(yōu)投資比例，如表2 所示.

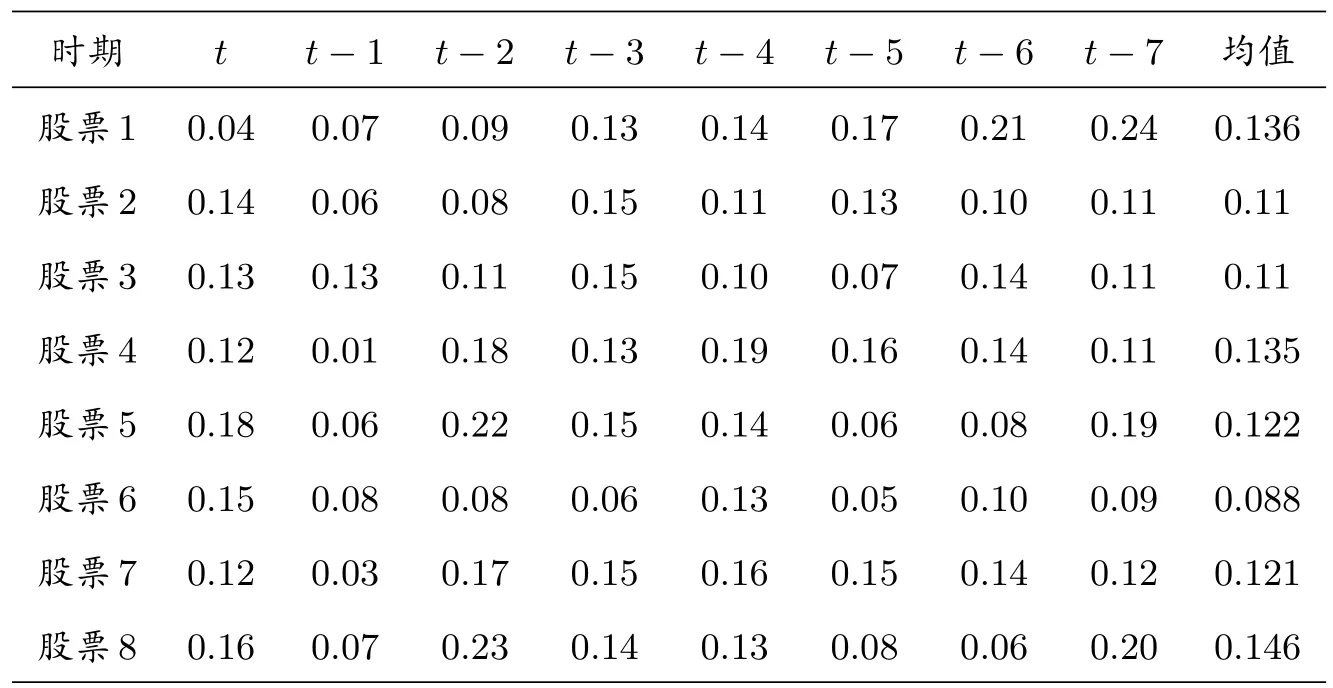
表1: 股票的收益和均值

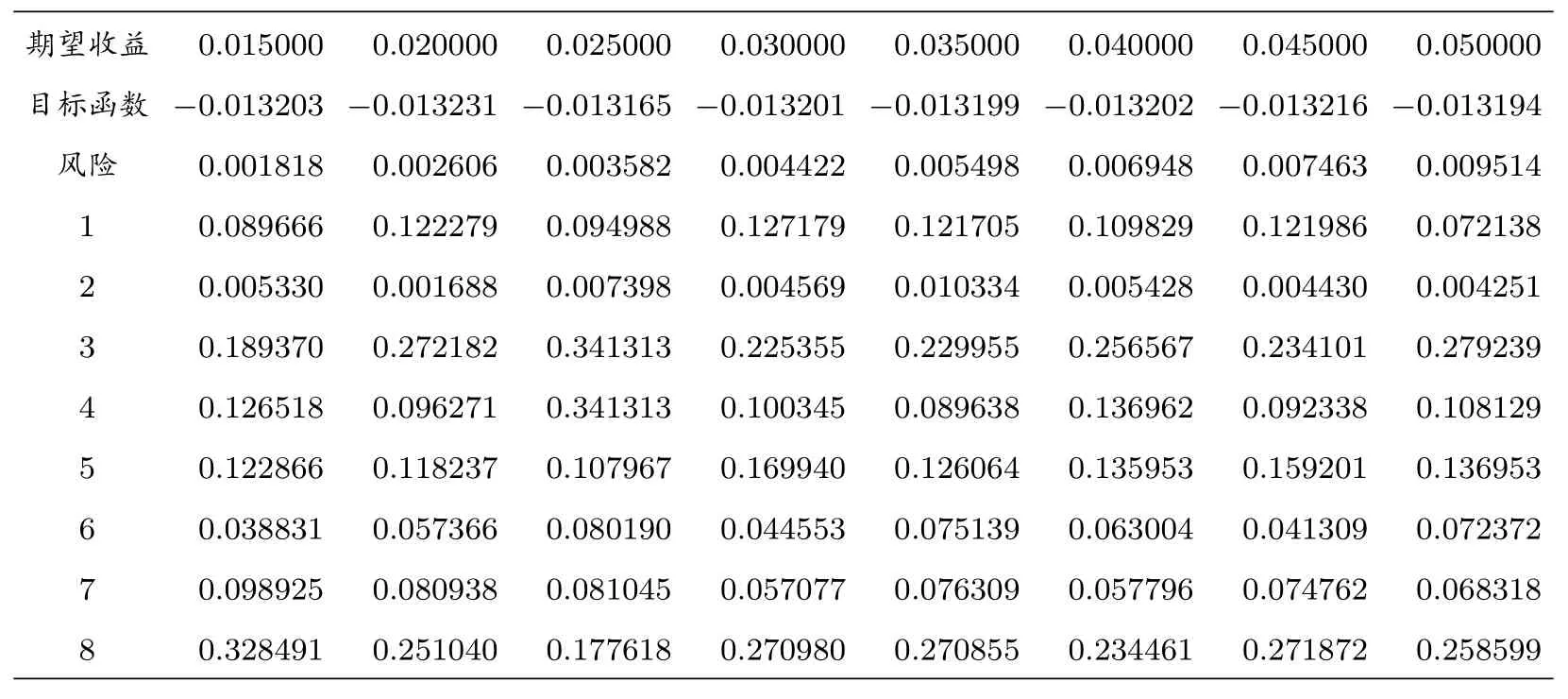
表2: 不同期望收益下的最優(yōu)投資組合

從表2 可以看出，投資組合的目標(biāo)風(fēng)險(xiǎn)隨著給定期望收益率的增加也在不斷地增加，符合證券市場(chǎng)上的實(shí)際情況.投資者若想得到較高的收益，則對(duì)第3 種和第8 種股票的投資比例相對(duì)增加，此時(shí)資產(chǎn)組合的風(fēng)險(xiǎn)也會(huì)相應(yīng)的增加.所以，投資者應(yīng)該結(jié)合自身的實(shí)際情況，設(shè)定符合自己實(shí)際的預(yù)期收益率.

圖2 為投資組合的有效前沿[14]，可以看出給定相同的期望收益率，考慮交易成本時(shí)的風(fēng)險(xiǎn)總比忽略交易成本時(shí)的風(fēng)險(xiǎn)大，此時(shí)的投資比例也有所不同.此外，當(dāng)期望收益率較低時(shí)，二者的風(fēng)險(xiǎn)差別不顯著，隨著收益率的增加，考慮交易成本的風(fēng)險(xiǎn)值增加較快，超過(guò)一定范圍后則相對(duì)穩(wěn)定，充分體現(xiàn)了交易成本在投資組合中的價(jià)值[10].

圖2: 有效前沿圖

4.3 算法優(yōu)越性比較

為了說(shuō)明教與學(xué)優(yōu)化算法的優(yōu)越性，在風(fēng)險(xiǎn)厭惡系數(shù)分別為A= 0.1,A= 0.3,A=0.5,A= 0.7 的情況下，把教與學(xué)優(yōu)化算法與粒子群算法在同等條件下迭代了120 次進(jìn)行了對(duì)比，如圖3 所示.

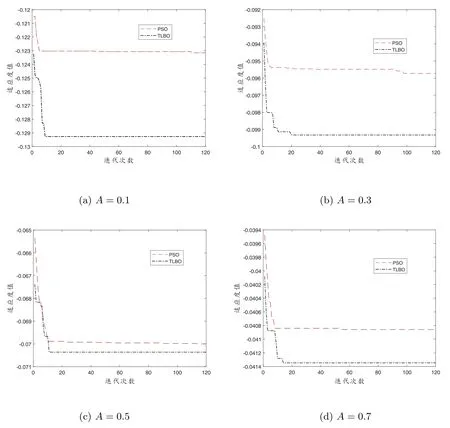
圖3: 不同風(fēng)險(xiǎn)厭惡系數(shù)下兩種算法的比較

從圖3 中的四個(gè)圖片中可以看出，在不同的風(fēng)險(xiǎn)厭惡系數(shù)下，教與學(xué)優(yōu)化算法的收斂性都優(yōu)于同等條件下的粒子群優(yōu)化算法.

5 結(jié)論

本文是在典型交易成本函數(shù)的基礎(chǔ)上，建立了含有典型交易成本函數(shù)的均值-方差-下半方差的投資組合模型，并采用教與學(xué)優(yōu)化算法對(duì)提出的模型進(jìn)行了求解.最后，進(jìn)行了實(shí)證研究.通過(guò)研究發(fā)現(xiàn)新建的模型可以說(shuō)明投資組合風(fēng)險(xiǎn)和收益之間的關(guān)系，為投資者決策提供了重要依據(jù)，并在不同的風(fēng)險(xiǎn)厭惡系數(shù)下，把教與學(xué)優(yōu)化算法和粒子群算法進(jìn)行了比較.