立足高考 領悟自招(四)
——自主招生怎么考熱學

■本刊編輯部

歷年自主招生真題中熱學部分試題涉及的主干知識點與高考考查的相同的有：分子動理論、理想氣體狀態方程、內能和熱力學第一定律、熱力學第二定律、熱機循環過程等。

一、以理想氣體為研究對象,考查氣體分子大小

例1(華約)在壓強不太大,溫度不太低的情況下,氣體分子本身的大小比分子之間的距離小很多,因而在理想氣體模型中可以忽略分子的大小。已知液氮的密度ρ=808.3kg/m3,氮氣的摩爾質量Mmol=28×10-3kg/mol。假設液氮可以視為是由立方體分子堆積而成的,請你根據所給數據對標準狀態下的氮氣進行估算,說明上述結論的合理性。

解析：標準狀況下氣體分子數密度n=,氮氣分子的間距,而液氮中單位體積的氮分子數,據此可以估算出液氮分子的直徑。d=8d′,可見氣體分子之間的距離比分子直徑大很多,即氣體分子本身的大小比分子之間的距離小很多,題中的結論是合理的。

點評:標準狀況下,相鄰分子間的平均距離D與分子直徑d的比值,因此在處理氣體問題時,可以把氣體分子視為沒有大小的質點;同時可以認為氣體分子除相互碰撞或者與器壁碰撞之外,分子力忽略不計,分子在空間內自由移動,也沒有分子勢能。

二、以水銀柱為研究對象,考查理想氣體的狀態方程

例2(上海交大自招)如圖1 所示,U形管豎直固定在靜止的平板車上,U 形管豎直部分和水平部分的長度均為l,管內充有水銀,兩管內的水銀面距離管口均為。若將U 形管管口密封,并讓U 形管與平板車一起做勻加速運動,運動過程中U 形管內水銀面的高度差為。求：

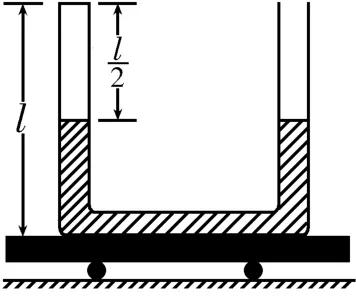
圖1

(1)平板車的加速度。

(2)U 形管底部中央位置的壓強。(設水銀的質量密度為ρ,大氣壓強恰好為p0=ρgl,空氣溫度不變)

解析：當平板車加速向右運動時,設左邊氣體壓強為p1,右邊氣體壓強為p2,U 形管橫截面積為S。

點評:水銀柱模型往往會結合物體平衡態或者加速運動狀態進行研究,在解決這類問題時往往存在一個假設,即氣體的物理狀態的變化是十分緩慢的,這就使得氣體有足夠的時間和外界進行熱交換,以保持封閉氣體的溫度不變。

三、以汽缸為研究對象,考查氣體的臨界問題

例3(北大保送考試)如圖2所示,汽缸上部足夠長,質量不計的輕活塞A、B的截面積分別為2S和S,汽缸下部長為2l。A、B活塞間以長為的無彈性輕質細繩相連,A活塞上部有壓強為p0的大氣。開始時封閉氣室M、N中充有同種密度的同種氣體,M的體積是N的2倍,N中氣體恰好為1mol,且小活塞B位于距底部l處,氣體溫度為T0。現同時緩慢升高兩部分封閉氣體的溫度至2T0,求平衡后活塞A到底部的距離。

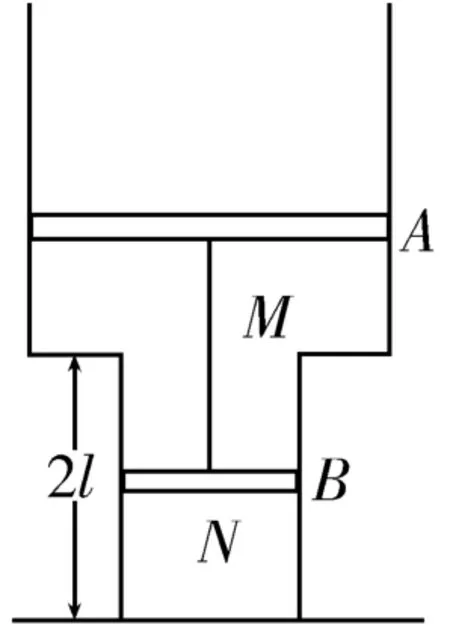
圖2

解析：初始時刻VM=2VN,而VN=lS,VM=lS+x·2S,解得。這表明開始時兩活塞的距離為,即開始時細繩處于松弛狀態,且pM=pN=p0。現同時緩慢升高兩部分封閉氣體的溫度,兩部分氣體都開始等壓膨脹。設小活塞B能夠上移的距離為l,細繩仍然未張緊,此時對應的溫度T′滿足,解得T′=2T0。對M中氣體有,解得。這表明在這之前細繩已經張緊。現設想升溫至2T0時刻小活塞B上移的距離為x,且x＜l(M、N兩部分氣體未混合),則對N中氣體有pN(l+x)S=nNR·2T0=2RT0,對M中氣體 有=nMR·2T0=4RT0,對A、B兩活塞有p0·2S+pM·S=pN·S+pM·2S,對N中氣體初態進行分析有p0lS=nNRT0=RT0,解得x=1.186l＞l。這表明升溫至2T0時,M、N兩部分氣體已混合。故p0[2lS+(x-2l)·2S]=(nN+nM)R·2T0=6RT0,且p0lS=nNRT0=RT0,解得x=4l。

點評:解決理想氣體的變化過程的關鍵在于抓住三個特殊的狀態,即初態、末態和臨界態。本題只有通過對臨界態的分析確定細繩的拉伸狀態和小活塞B所處的位置,才能得到正確的結果。

四、以汽缸為研究對象,考查熱力學第一定律

例4(博雅計劃)如圖3所示,有一個頂部開口、橫截面積為S的絕熱圓柱形容器,放在水平地面上。容器內有一質量為m的勻質絕熱擋板在下,另一個質量可忽略的絕熱活塞在上,活塞與容器頂端相距甚遠。擋板下方容積為V0的區域內,盛有摩爾質量為μ1、摩爾數為v1的單原子分子氣體；擋板與活塞之間容積為V0的區域內,盛有摩爾質量為μ2、摩爾數為v2的雙原子分子氣體。擋板和活塞與容器內壁之間無縫隙,且都可以無摩擦地上下滑動。設兩種氣體均處于平衡狀態,而后將擋板非常緩慢、絕熱且無漏氣地從容器壁朝外抽出,最終形成的混合氣體達到熱平衡態。設整個過程中雙原子分子的振動自由度始終未被激發。將大氣壓強記為p0,設,將μ1、v1、μ2、v2、p0、V0處理為已知量。

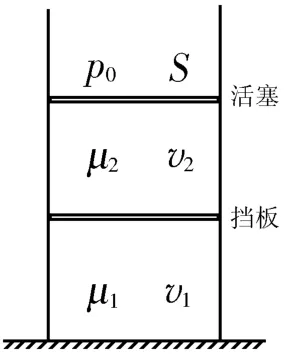
圖3

(1)將末態混合氣體內的單原子分子氣體和雙原子分子氣體的密度分別記為ρ1和ρ2,試求ρ1∶ρ2。

(2)求混合氣體的體積V。

解析：(1)擋板上方氣體壓強p2=p0,擋板下方氣體壓強,因為,所以ρ1∶ρ2=μ1v1∶μ2v2。

(2)因為雙原子分子的振動自由度未被激發,所以不考慮振動,即1mol雙原子分子氣體的內能為,1mol單原子分子氣體的內能為,設末態混合氣體的溫度為T,由理想氣體的狀態方程得p0V=(v1+v2)RT,系統內能的改變量,對擋板上方氣體有p2V0=v2RT2,對擋板下方氣體有p1V0=v1RT1,所以。外界對氣體做功W=p0(2V0-V),由熱力學第一定律W=ΔU,解得。

點評:在解決涉及能量變化的熱力學問題時,需要綜合應用熱力學第一定律和理想氣體的狀態方程求解相關物理量。

五、借助圖像,考查熱機的循環過程

例5(卓越)如圖4所示,一定質量的理想氣體由狀態a經過Ⅰ、Ⅱ兩過程到達狀態c。其中Ⅰ為等溫過程；Ⅱ為先經過等壓過程至狀態b,再經過等容過程至狀態c。則該氣體( )。

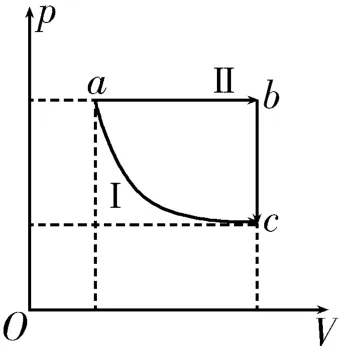
圖4

A.在過程Ⅰ中吸收的熱量大于在過程Ⅱ中吸收的熱量

B.在過程Ⅰ中吸收的熱量小于在過程Ⅱ中吸收的熱量

C.在過程Ⅰ中對外做的功大于在過程Ⅱ中對外做的功

D.在過程Ⅰ中對外做的功小于在過程Ⅱ中對外做的功

解析：在p-V圖像中對外做的功對應面積,故在過程Ⅱ中做功較多。內能只與狀態有關,與具體過程無關,即兩個過程從a狀態到c狀態內能都不能變,由Q=ΔU+W可知,在過程Ⅱ中一定比在過程Ⅰ中吸熱多。

答案：BD

點評:在熱機的循環過程中,若循環沿順時針方向進行,則系統對外所做的功為正;若循環沿逆時針方向進行,則系統對外所做的功為負。如果構成一個循環過程,若循環沿順時針方向進行,則閉合曲線所圍的面積就是系統對外界做正功;若循環沿逆時針方向進行,則閉合曲線所圍的面積就是外界對系統做正功。

六、借助前沿信息,考查建模能力

例6(清華自招)就黑體輻射而言,輻射最大波長λmax滿足λmaxT=b(T為黑體的熱力學溫度,b是常量),同時黑體單位面積上的輻射功率P=σT4(σ為常量)。已知人體的λmax1=9.6μm,太陽的λmax2=509.6nm。

(1)如圖5 所示,真空中有四塊完全相同且彼此靠近的大金屬板A、B、C、D平行放置,表面涂黑(可以看成黑體),最外側兩塊板的熱力學溫度各維持為T1和T4,且T1＞T4。當達到熱穩定時,求B板的溫度。

(2)火星到太陽的距離為400R(R是太陽的半徑,為696300km),認為火星受熱的面積為πr2(r為火星的半徑,為3395km),把火星看成黑體,估算火星表面的溫度。

圖5

解析：(1)對一個物體來說,吸收熱量和輻射熱量是同時進行的。溫度為T2的B板左側單位時間內凈獲得的輻射熱量Q2左=,B板右側單位時間內凈獲得的輻射熱量,達到熱穩定時應有Q2左+Q2右=0,解得。同理,對溫度為T3的C板有,解得。

(2)由λmax1T1=λmax2T2=b,以及人的體表溫度T1=310K,解得太陽的溫度T2=5840K。熱穩定時,火星吸收太陽光的功率,火星輻射的功率·4πr2,且,解得火星表面溫度T′=210K。

點評:這是一個信息給予題,根據題目提供的信息,正確建立輻射模型并明確熱平衡的條件即可順利求解。