一道含參函數問題的兩種解法的比較

■梁立揚(指導老師:褚人統)

例題已知a＞0,f(x)=ln(2x+1)+2ax-4aex+4。當a=1 時,f(x)的最大值為0。若函數f(x)的零點個數為2,求a的取值范圍。

解法一：(常規解法),當a＞0,且時,f″(x)＜0,所以f′(x)在上為減函數。

①當a=1時,f(x)只有唯一零點。

②當0＜a＜1 時,f(0)=4-4a＞0,即f(x0)＞f(0)＞0,此時有2個零點。

③當a＞1 時,2a-4aex0=0。

f(x0)=ln(2x0+1)+2ax0-4aex0+。

又有f′(0)=2-2a＜0,故。

令g(x)=ln(2x+1)+2ax-,則g′(x)=,故g(x)在定義域內單調遞增。

而g(0)=2-2a＜0,故g(x)＜0,于是f(x0)＜0,所以當a＞1時不存在零點。

解法二：(利用偏導數求解)令z=f(x)=ln(2x+1)+2ax-4aex+4,則za=z′a=2x-4ex(za以a為自變量,zx以x為自變量),表示固定某x時,a方向斜率的增速)。

當x=x0時,4ex0為一常數且小于0,,所以原式z(a)遞減(a為自變量,x=x0為常數)。

當a=1時,f(x)max=0。

所以當a=1時,f(x0,a)≤0。

又f(x)=ln(2x+1)+2ax-4aex+4(a＞0),并且,

所以僅當0＜a＜1 時,存在f(x)＞0(x=x0)(x為自變量,a為常數),當0＜a＜1時,存在有2個零點(如圖1所示)。

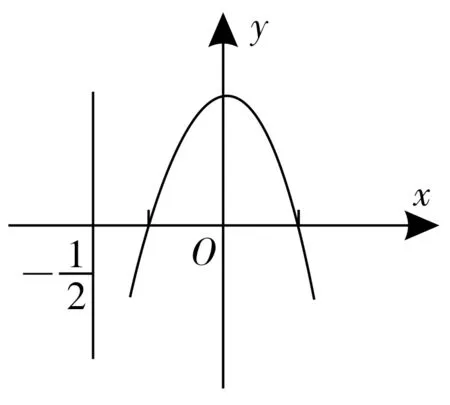
圖1

總結：兩種方法相比較,利用偏導數求解時的運算過程更加簡潔。很多高中數學問題都可以采用多種方法解決,所以同學們在做題時,不能僅僅滿足于一道問題的解答,而應該關注同一道問題可以采用哪些不同的方法解答,并比較不同解法的優缺點,拓展思維的寬度。同時同學們也不要局限于對課本知識的學習,也可適當關注導數、泰勒公式、柯西不等式等這些高等數學知識,因為在解決數列放縮、不等式證明等問題時,通常可以使大家站在更高的角度看問題,更好地解答問題。