一種基于凝固地理系的捷聯慣導極區導航算法

中國空空導彈研究院，洛陽 471000

地球的兩極地區存在豐富的自然資源。出于科學、經濟、軍事戰略等方面的考量，世界大國在兩極地區均從事著勘測活動。在南極地區各國建設的機場有50座之多，美國擁有13座，俄羅斯有8座，英、法、德、日等國均有極地機場，我國也正在建設第一座永久性南極機場。這對導航技術提出了更多的要求，需要飛機與艦船具備極區導航能力。

目前，隨著中國對兩極地區經濟以及軍事需求的增加，國內對極區導航領域的研究也漸漸活躍。由于中國地理位置遠離極地，客觀上造成對極區探索的不足，對極區的研究也相對滯后，研發的航空慣導系統也不具備極區飛行的能力。

傳統的指北方位平臺慣導力學編排在高緯度地區存在方位陀螺施矩困難的問題，捷聯慣導則存在計算溢出問題。在高緯度地區緯度圈越來越小，最終收于一點，沿著緯度圈的運動半徑也最終變為零：

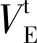
為了解決這個問題，游動方位慣導系統和自由方位慣導系統被提出。這兩種方法可以解決慣性導航系統在極區遇到的上述問題，但由于在地理極點附近，由于真北方向失去定義導致自由方位角和游動方位角失去定義，航向無法給出，即采用這兩種機械編排的慣性導航系統能夠實現在地理極點附近導航上不出現奇點，但從方向余弦矩陣中提取航向和位置信息時存在奇異值。

為此，又提出了以下幾種適用于極區的慣性導航方法：文獻 [1-2]提出了格網導航, 這是目前比較成熟的一種極區導航方案，基于圓球模型的力學編排存在原理性誤差，而基于橢球模型的力學編排非常復雜、計算量大。文獻[3-9]提出了橫向經緯度導航, 橫向經緯度導航將地球模型當作圓球模型，通過坐標變換將極點轉換到赤道上，解決了高緯度地區的導航問題，同樣存在著原理性誤差。

文獻[10]提到了極區平面導航，介紹的極圈力學編排采用了與本文相同的坐標系為導航參考坐標，但是將其簡化為了平面導航，存在原理性計算誤差。

本文在過去極區導航發展的基礎上，以實用、簡化算法為出發點，提出一種新的基于凝固地理系的極區導航新方法，該導航模型基于現有橢球模型，無原理性誤差，計算量小，是一種傳統地理系與凝固地理系的融合極區導航算法，能夠滿足捷聯慣導極區長航時導航需求。

1 凝固地理系下導航算法

凝固地理系(用n表示)定義如圖1所示，該坐標系原點位于坐標建立時刻橢球上，軸向與坐標原點處地理系(用t表示)重合，相對于地球固定不動，X、Y、Z對應于北、天、東方向。CGCS2000地球系(用e表示)簡稱為地球系，機體系用b表示。

圖1 凝固地理系Fig.1 Frozen geography frame

傳統指北方位導航力學編排如下：

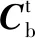
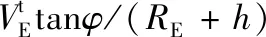
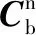
由于凝固地理系與坐標系建立時刻的地理系重合，地理系下導航參數可以直接作為到凝固地理系導航參數的初值，無需換算；凝固地理系下導航算法相對于指北方位導航算法也更簡化。

2 導航參數在不同坐標系下換算

凝固地理系與地理系轉換矩陣轉換關系如圖2所示。

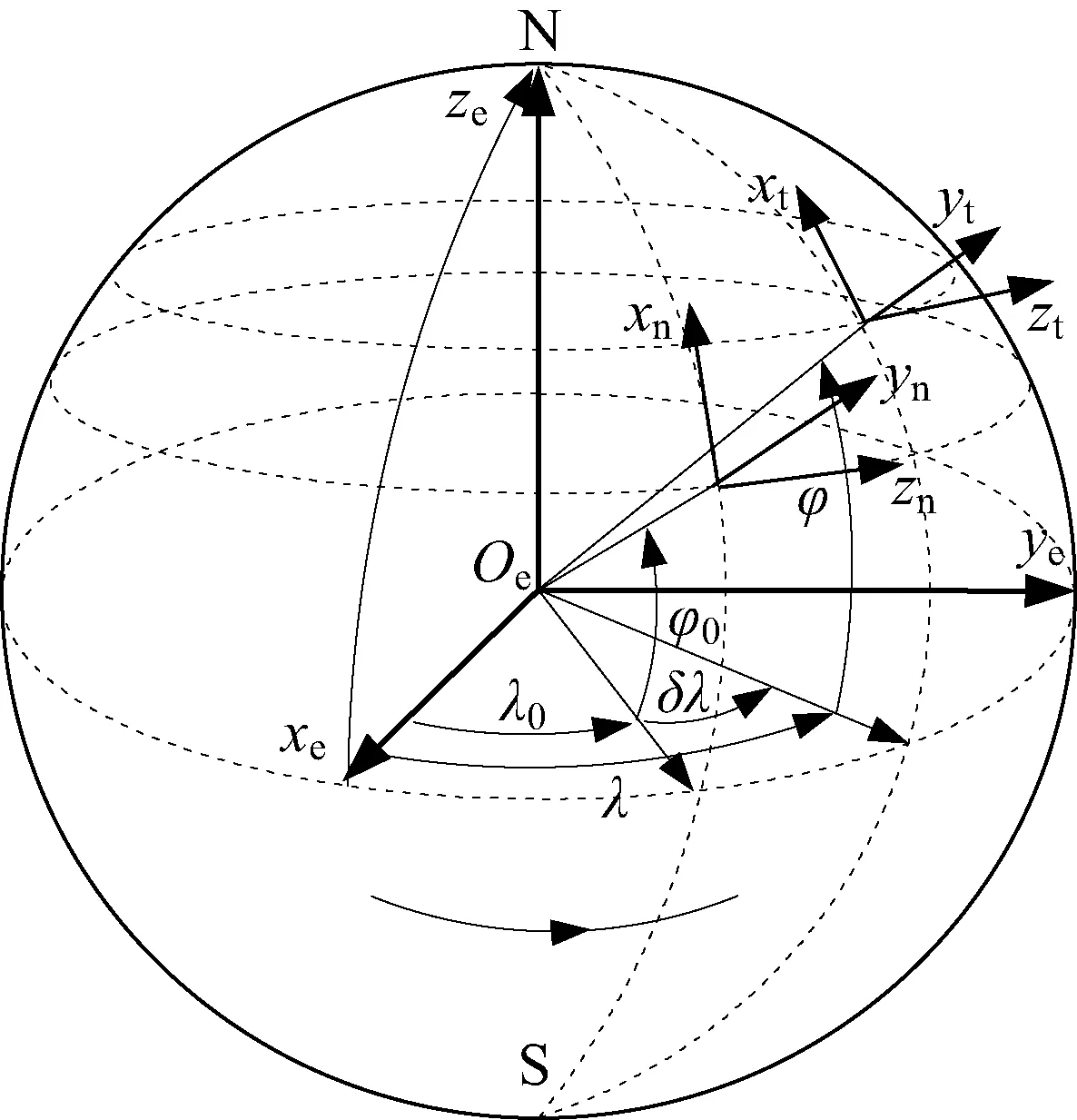
圖2 地理系與凝固地理系坐標轉換Fig.2 The conversion relation between geography frame and frozen geography frame

凝固地理系導航計算的位置是相對于原點的三軸位置，短距離導航中姿態、速度與地理系導航結果基本一致，可以直接用于描述載體運動狀態。

為了便于在不同坐標系下對載體運動進行描述，以下將對凝固地球坐標系導航參數與其他坐標系換算進行說明。

地理系到凝固地理系的換算過程為z軸旋轉緯度值φ，繞-x軸旋轉經度差δλ，再繞-z軸旋轉緯度值φ0。

三次旋轉可用旋轉矢量表示：

合成四元數為：

Qtn=Q1·Q2·Q3=

用轉換矩陣方式可以表示為：

(1)凝固地理系與地球系轉換矩陣

換算公式如下：

(2)位置換算

凝固地理系下位置換算到地球系，公式為：

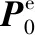
地球系下三維坐標換算到地理系有成熟的算法可用，但是常規算法需要迭代計算，這對于在線實時計算來說是一個計算隱患，會有進入死循環的可能，工程上不推薦使用。

采用如下公式無需循環算法，在實際編程時采用atan2替代atan以實現無奇點計算。

Re=6 368 137 m

Rp=6 356 752.314 2 m

λ=arctan (Y/X)

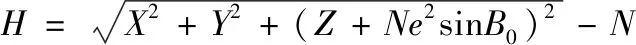
(1)

(3)速度換算

(4)地理系下姿態計算

Q=Qtn·Qnb

提取的航向、俯仰與滾動角公式如下：

θ=arcsin 2(Q1Q2+Q0Q3)

(5)凝固地理系到橫軸地球坐標系的換算

對于有橫向經緯度導航需求的應用環境，凝固地理系下導航參數可以借助地理系進行換算以獲得橫軸坐標系下參數，見文獻[4]，而無需將核心導航算法修改為有原理性誤差的橫向經緯度力學編排。

本文給出一種凝固地理系到橫軸地球坐標系位置的直接轉換算法，公式如下：

橫向地球系高度直接利用公式(1)進行計算。

速度與姿態計算公式見文獻[4],其中地理系下經緯度，使用坐標原點的經緯度。

(6)凝固地理系到格網系導航參數的換算

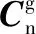
通過以上換算，可以保持核心算法與軟件不變，就可以滿足其他導航方式的需求，關鍵在于不存在原理性誤差。

3 軟件流程

兩種導航坐標系下的導航算法在經過某個緯度圈時進行坐標系與算法的切換，本文采用圖3所示流程進行設計。其中a為設定的采用凝固地理系導航坐標系緯度點，b為凝固系坐標導航退出緯度點，并且a>b，這兩者設定為一個小偏差，比如為6′。這樣的設定是防止邊緣飛行時，出現算法頻繁切換。

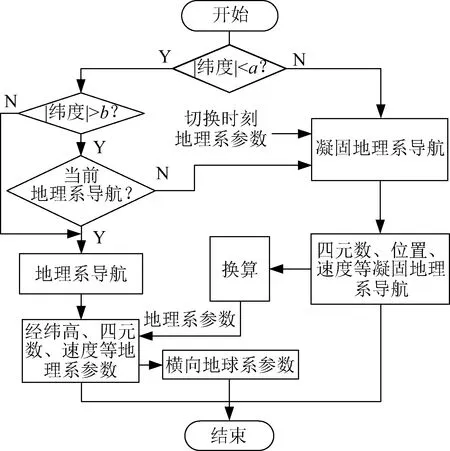
圖3 算法與軟件設計切換流程Fig.3 Algorithm and software switching process

4 仿真校驗

(1)切換點緯度的確定

指北方位導航在接近極點時，由于正切函數原因導致計算溢出，所以當緯度增大到特定值時刻切換為凝固地理系導航，以規避該問題。

正切函數在角度越接近90°過程中數值快速增大直至無窮。經過數值計算可以確定指北方位系統導航方程89.5°附近，并不會出現計算溢出，選擇88°～89.5°緯度圈較為恰當。本文確定以89.5°緯度圈為坐標系切換線，即高于該緯度后將指北方位導航切換為凝固地理系導航。

(2)導航仿真

為驗證捷聯慣導系統導航算法在極區的正確性以及性能，需要進行仿真試驗。為避免數值求解在極區遇到的問題，通過解析法給出陀螺和加速度計的輸出。

本文采用沿經線向北飛越極點，然后飛出極區的軌跡。仿真參數設置如下：初始緯度89°，經度120°，飛行高度1 000 m，北向飛行速度100 m/s，保持勻速直線平飛，無慣性器件誤差，仿真總時間設定為2 000 s。仿真時間558～1 676 s內為進入與飛出89.5°緯度圈的時間，即凝固地理系下導航時間段，約1 117 s為穿越極點時刻，其余時間為指北方位北天東地理系下導航時間。

凝固地理系位置導航參數見圖4。

圖4 凝固地理系下位置Fig.4 The position under frozen geography frame

圖中可見凝固地理系導航系下保持了無東向運動，由于地球曲率影響，凝固地理系下高度一直在下降。進入與飛出89.5°緯度圈，X軸的運動距離約為110 km。

凝固地理系姿態變化見圖5。

圖5 凝固地理系下姿態Fig.5 The attitude under frozen geography frame

圖中可見凝固地理系下載體俯仰角一直負向變化，航向與橫滾角一直保持不變。

為了形成完整不間斷的地理系參數，需要將凝固地理系下參數轉換至地理系，以形成完整的指北方位參數，地理系下位置信息如圖6所示。

圖6中可見飛過極點時經度從120°立即跳變為-60°；飛行高度維持在1 000 m。

地理系下姿態如圖7所示,圖中可見航向角飛過極點后，立刻從北向0°切換為南向-180°方向。

下面將對導航誤差進行計算，將全段經緯高參數轉換至地球系下與軌跡進行對比，姿態信息在地理系對比以分析算法誤差特性。

地球系下位置誤差如圖8所示。

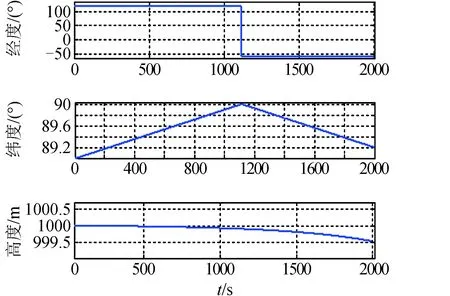
圖6 地理系下位置Fig.6 The position under geography frame

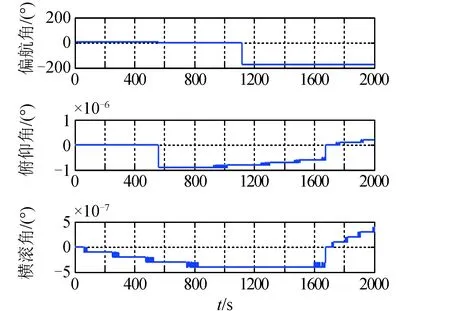
圖7 地理系下姿態Fig.7 The attitude under geography frame

圖8 地球系下位置誤差Fig.8 The position error under the earth frame

從圖8中可見導航坐標系切換過程并不影響慣導誤差發散的趨勢與大小，位置誤差變化保持連續，無跳點。

地理系下姿態誤差如圖9所示。

圖9 地理系下姿態誤差Fig.9 The attitude error under geography frame

5 結束語

凝固地理系導航是在指北導航力學編排基礎上，刪除會導致計算溢出項。依舊按照地球的橢球模型進行導航，不存在原理性誤差。

原理上凝固地理系屬于地球系的一種，是將原點從地心挪到了橢球面，其力學編排適合全球導航，但是過長距離導航將使得凝固地理系下導航參數失去直觀的物理意義，最終要將參數轉換到地理系下才能表征載體的運動狀態。將該坐標系用于距離原點200～300 km內的導航是必要的。本文以89.5°緯度圈為界限，直徑約為110 km；在載體位置低于該緯度圈后切換回原來導航坐標方案，這是一種恰當的極區導航解決方案。仿真和分析結果表明：本方案導航算法簡單，計算量小，導航精度高，無原理性誤差。

本文與其他極區導航方法的不同，在于不追求形式上的全球統一方法，該坐標系的使用限于極區小范圍，超出范圍仍舊切換回通用的地理系。