基于Pareto支配的MPRM電路面積與功耗優化*

閆盼盼，俞海珍，史旭華，萬 凱

(寧波大學信息科學與工程學院，浙江 寧波 315211)

1 引言

隨著集成電路(IC)技術的發展，電路集成度正在迅速增加[1,2]。功耗和面積已經成為IC設計中不容忽視的問題，在電路設計流程的各個階段都需要考慮電路面積和功耗。

任何邏輯電路都可以由基于AND/OR/NOT形式的布爾邏輯，也可以由基于AND/XOR或OR/XNOR形式的RM(Reed-Muller)邏輯來表示。隨著集成電路優化設計的發展，以RM邏輯表示的邏輯電路在功耗、面積、速度和可測試性方面比用傳統布爾邏輯表示的邏輯電路更具優勢[3]。

RM邏輯主要分為固定極性RM FPRM(Fixed-Polarity Reed-Muller)和混合極性RM MPRM(Mixed-Polarity Reed-Muller)。MPRM展開式的極性搜索空間龐大，包含了FPRM展開式的所有極性。因此，MPRM具有比FPRM更大的優化空間和更好的優化效果。極性直接決定MPRM邏輯電路的表達形式，然后影響電路的面積和功耗，并且其優化是在特定空間中搜索1個或多個極性，使其目標函數獲得最優值。但是，MPRM電路也有其劣勢，它的極性搜索空間龐大，使其電路性能優化的時間和空間復雜度很高。因此，需要尋找一種有效的算法來解決MPRM邏輯電路的這個問題。粒子群算法、遺傳算法、免疫算法都是目前比較常用的智能算法[4 - 6]。由于粒子群算法相比其它算法具有收斂速度快、魯棒性好等優點，獲得了越來越多的關注。此外，它具有內在的并行搜索機制，特別適用于傳統方法難以解決的復雜優化問題。國內外很多學者對粒子群算法進行研究，取得了一些成果。文獻[7]提出一種多目標量子粒子群算法，采用共享學習機制和雙勢阱模型避免算法發生過早收斂；文獻[8]提出了一種分群多目標粒子群算法，采用向量法劃分子區域，不同子區域采用不同的搜索策略進行尋優操作，保持算法的多樣性；文獻[9]提出了一種三值多樣性粒子群算法，采用廣泛學習策略和三值變異操作進行算法改進，以保持種群多樣性策略，從而有效地克服算法的早熟收斂問題。

綜上所述，本文在離散三值粒子群優化算法研究的基礎上，結合混合極性的特征，對文獻[9]中采用三值多樣性粒子群算法求解MPRM電路綜合優化問題主要作了如下改進:(1)采用Pareto支配關系構造外部集；(2)采用快速排序的方法在種群中搜索非支配解集；(3)對粒子進行邊界約束處理。通過加入上述3種改進策略，提出一種多目標三值多樣性粒子群MOTDPSO(Multi-Objective Ternary Diversity Particle Swarm Optimization)算法。利用MOTDPSO算法對MPRM電路進行最佳功耗和面積的綜合優化，得到Pareto前沿，實現面積和功耗的折衷優化，并通過實驗進行了驗證。粒子的位置、速度更新公式參考文獻[9]。

2 MPRM電路面積和功耗估計模型

在混合極性OR/XNOR電路中，對于任意1個n變量的邏輯函數極性P對應的OR/XNOR展開式如式(1)所示：

(1)

由式(1)可知，OR/XNOR電路實際是由多輸入XNOR 和OR操作組成的，而多輸入的XNOR 和OR操作可以分解為二輸入的XNOR 和OR操作，二輸入的XNOR 和OR操作項數之和則表示電路面積。

多輸入OR操作分解如式(2)所示，根據式(2)，Si可由mi個二輸入OR操作得到。

(2)

多輸入XNOR 和OR操作具體分解如式(3)和式(4)所示，根據式(3)和式(4)將多輸入XNOR 和OR操作分解成二輸入OR操作和二輸入XNOR操作，它們的最終項數可表示為:

(3)

(4)

混合極性OR/XNOR電路面積Earea可表示為:

Earea=No_of_OR+No_of_XNOR=

(5)

目前集成電路的主要形式是CMOS電路，對于一個由n個門組成的電路，其總動態功耗的表達式為:

(6)

(7)

在式(7)中可看到，開關活動性的大小僅與P(g)有關，P(g)是輸出信號g的概率。根據文獻[10，11]可將多輸入XNOR和OR分解為一系列二輸入XNOR和OR。分解完成后，把XNOR門和OR門的開關活動性進行相加，從而得到整個MPRM邏輯電路的開關活動性，通過開關活動性的總和來權衡電路的功耗。

3 基于MOTDPSO算法的MPRM電路面積與功耗優化

3.1 基于Pareto支配的三值粒子群算法

在用Pareto支配概念進行算法改進的過程中，涉及3個集合：

(1)種群：由算法中的所有粒子組合而成。

(2)非支配集：保存了每一代中的非支配解。

(3)外部集：保存了種群從初始到目前搜索到的所有非支配解。

上述3個集合中，非支配集是保存種群的每一代的非支配解的集合。外部集的更新是通過非支配集按照支配關系插入外部集，進而構成新的外部集。種群更新是由于個體和全局最優位置的更新。

3.1.1 邊界約束處理

部分粒子會超出定義的邊界范圍，這種情況會發生在粒子進行速度、位置更新以及變異的過程中，這樣可能導致的結果是，最終搜索到的最優值不在定義域范圍內。本文采用式(8)進行處理：

(8)

其中，[xmin,j,xmax,j]表示第j維的取值范圍。

如果經過運動之后粒子到了一個新的位置，此時超出了邊界，可將粒子設定在邊界上，使得粒子的速度大小減為原來的一半，方向與原來反向。

3.1.2 非支配集

本文中非支配集的構造采用快速排序的方法，如算法1所示。

算法1 構造非支配集

Step 1 選擇1個個體i∈S，并且i為種群S的第1個個體；

Step 2 將選擇的第1個個體i與種群中其他個體進行比較,S被分為patr1和part2。

Step 2.1 如果part2被i支配,即i支配part2，清除part2;

Step 2.2 如果part1不被i支配，保留part1；

Step 2.2.1 如果i不被part1中其他個體支配，將i放入非支配集NP中；

Step 2.2.2 如果i被part1中其他個體支配，清除i；

Step 3S=patrt1，重復上述過程，直到S=?。

3.1.3 個體最優位置

根據PSO算法的原理，個體最優位置可解釋為個體i從初始化到目前為止的最優位置，如式(9)所示：

(9)

式(9)解釋為，如果粒子i支配個體最優位置，粒子i的當前位置就被定為個體最優位置；如果粒子i不支配個體最優位置，則個體最優位置保持不變。

3.1.4 外部集

本文中，外部集的更新是通過非支配集按照支配關系插入外部集，進而構成新的外部集。如算法2所示。

算法2 外部集的選取

Step 1 當外部集為?時，將初始種群的非支配集NP中的個體放入外部集中；

Step 1 當外部集不為?時，選取1個個體i∈NP，將i與外部集中的個體進行比較支配關系；

Step 2.1 如果i被外部集中的某些個體支配，則i不能進入外部集；

Step 2.2 如果i不被外部集中的某些個體支配，將i放入外部集，外部集中被個體i支配的那些個體要被剔除；

Step 3 重復上述循環直至比較完畢。

3.1.5 全局最優位置

全局最優位置是從外部集中選取的。算法開始時，全局最優位置為粒子本身位置；接著，在每一代中，先計算擁擠距離，按照擁擠距離對外部集進行降序；然后從外部集的前10%的粒子中隨機選擇1個粒子的位置為全局最優位置。

3.2 MOTDPSO算法在MPRM電路綜合優化上的應用

結合以上所述的三值多樣性粒子群算法和混合極性OR/XNOR電路的極性轉換，本文提出了一種改進的三值粒子群算法，將該算法應用于MPRM電路功耗和面積優化。算法流程具體描述如圖1所示。

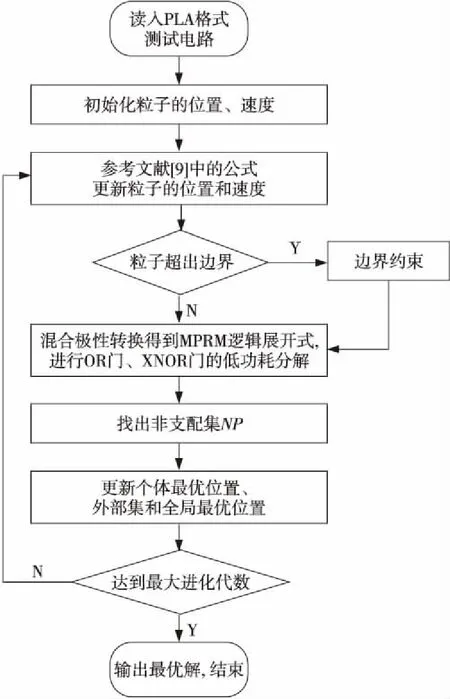
Figure 1 Flow chart of MPRM circuit power consumption and area optimization based on MOTDPSO algorithm圖1 MOTDPSO算法優化MPRM電路功耗和面積流程圖

4 實驗數據與分析

本文用C語言實現MOTDPSO算法，在Windows 10操作系統下，通過VS2010編譯，程序的硬件環境為Intel(R) Core(TM)i5-8250U@1.60 GHz 8 GB RAM，測試電路均采用PLA格式MCNC基準電路,對18個MCNC電路進行了面積與功耗優化，得到了Pareto最優解集和Pareto前沿。

圖2給出了電路rd530、5xp10以及misex10的Pareto前沿。從圖2中可以看出，這3個電路的面積與功耗的Pareto前沿不是嚴格的凸函數，其余電路的Pareto前沿也是如此。這也證實了使用Pareto支配進行MPRM電路面積與功耗優化的重要性。

Figure 2 Pareto frontier of MPRM circuit area and power consumption圖2 MPRM電路面積與功耗Pareto前沿

表1給出了在18個MCNC電路上運行MOTDPSO算法的結果，其中“benchmark”表示測試電路的名稱，“inputs”表示測試電路的輸入變量個數；“N_PF”表示Pareto最優解集的大小；“面積增加”和“功耗減少”分別表示所選擇的最優解相對于面積最小解所引起的面積增加和功耗降低的比率。“所選擇的最優解”是根據效率因子“E=功耗減少/面積增加”所選取的最終解，其選取的原則：(1)如果存在E>1的最優解，則所選擇的最優解要使E的值最大化；(2)如果不存在E>1的最優解，則所選擇的最優解就是面積最小解。此原則是基于以盡可能小的面積開銷獲得更低的功耗。

從表1可以看出，這18個電路的Pareto最優解集都包含多個非支配最優解，特別是table3，其非支配最優解的數量達到了62個。這也證實了使用Pareto支配概念進行MPRM電路面積與可靠性優化的有效性。

根據效率因子E所選擇的最終解中，有3個電路所選擇的最優解就是面積最小最優解，因為找不到E小于1的最優解，換句話說，雖然可以降低功耗，但是面積開銷較大。對于剩余的15個電路，所選擇的最優解的E均大于1；特別是t481，在不到1%的面積開銷下，功耗減少了4.26%，其最終解的E為4.84。對于表1的電路，從平均值看，相對于面積最小解，所選擇的最終解面積增加了5.30%，并且功耗減少了8.18% 。

Table 1 Area and power consumption optimization results using MOTDPSO algorithm表1 MOTDPSO算法面積與功耗優化結果

為了進一步驗證MOTDPSO算法求解MPRM電路面積與功耗優化的有效性，將其與NSGA-II[12]算法進行實驗比對。將上述2種算法分別測試20次,對20次結果的最優解求平均值。表2給出了在18個MCNC電路上運行上述2種算法的結果。表中“benchmark”和“inputs”分別為測試電路的名稱和輸入變量個數，“area”和“power”分別為測試20次電路最優解的平均面積和功耗，“S(area)”和“S(power)”表示電路面積和功耗的優化率，計算公式如下所示：

(10)

(11)

其中，SA1(SP1)、SA2(SP2)分別表示對NSGA-II和MOTDPSO算法測試20次搜索到的最優解的平均面積和功耗。

由表2可知，MOTDPSO算法相比NSGA-II算法能獲得更小的電路面積和功耗。比如pcle電路，MOTDPSO算法相比于NSGA-II算法面積和功耗分別優化了8.50%和13.83%。在misex3電路中，即使MOTDPSO算法搜索到的最佳極性電路面積有所增加，但功耗減少了。根據18個Benchmark電路的測試結果可知，MOTDPSO算法相比NSGA-II算法，電路面積與功耗平均優化率分別為4.29%和6.02%。最后，將2種算法運行20次的面積與功耗進行方差計算，NSGA-II算法面積與功耗方差為5.64和8.56，MOTDPSO算法面積與功耗方差分別為4.87和6.35，所以MOTDPSO算法具有良好的魯棒性。

5 結束語

針對MPRM電路的面積與功耗綜合優化問題，本文提出了一種基于MOTDPSO算法的MPRM電路面積與功耗最佳極性搜索方案。在三值多樣性粒子群算法求解MPRM電路綜合優化問題的基礎上，對超出定義的邊界范圍的粒子執行邊界約束處理，并結合Pareto支配概念來改進算法;然后建立了基于Pareto支配的三值粒子群算法的粒子與MPRM電路極性之間的參數映射關系，并結合面積與功耗估計模型以及 OR/XNOR電路混合極性轉換方法，將該算法應用于MPRM電路的功耗和面積優化。最后對18個PLA格式MCNC Benchmark電路進行測試，與NSGA-II算法搜索到的最優解相比，MOTDPSO算法有較好的優化效果和魯棒性。

Table 2 Optimal solution data and optimization rate of MOTDPSO and NSGA-II algorithms表2 MOTDPSO與NSGA-II算法最優解和優化率