基于遺傳算法的散貨船配載軟件的開發

薄志斌，胡 義

(武漢理工大學 能源與動力工程學院，湖北 武漢 430063)

0 引言

傳統的配載方案一般是由大副或港口工人通過經驗憑借手工方式完成，這樣的配載方案一方面耗時耗力，另一方面由于人工的疏忽會出現計算偏差。船舶貨運量的大幅增加和航次路線的越來越復雜，使得傳統方案越來越不適合當今的發展趨勢[1]。

國外，早在20世紀90年代中期就開始研究散貨船的配載并在計算機上開發相關的配載軟件,其中:德國的SCHIFFKO公司開發了基于DOS環境的船舶計算軟件；挪威的Autoship Systems Corporation公司開發出一款名稱為Autoload的船用裝載儀[2]。國內，大連海事大學史國友教授分析了貨物在散貨船的實際裝載情況，建立約束條件，然后用靜水力數據開發出散貨船配載儀。另外，還有福海船舶配載儀，這是一款涵蓋了谷物穩性計算和破艙穩性計算等很多實用功能的裝載軟件。

為此，從20世紀90年代起，散貨船的配載優化和自動化配載就已經成為了相關領域內的研究熱點。隨著計算機的廣泛應用，關于船舶配載的軟件也慢慢開始出現，可以通過手動輸入船舶的一些參數來完成配載的計算，但是這種配載方案仍然需要人工的干預調整，才能計算出最優的結果。近幾年來隨著人工智能的不斷發展，該技術也逐漸在航海領域得到了廣泛的應用，散貨船的智能配載研究就是人工智能在航運業上的一種重要應用。智能化的配載方案不僅可以提高船舶在航行過程中的穩性和強度等，有利于船舶的運輸安全，并且還會提高配載效率，降低船舶的運營成本[2]。本文從當前的配載軟件市場出發，引進遺傳算法對散貨船配載進行研究，主要對配載系統中的約束條件從適應度縮放、模擬退火拉伸、加入精英保留法三個方面對配載系統進行研究。

1 散貨船的遺傳算法優化

1.1 遺傳算法的主要操作

遺傳算法的基本操作步驟：選擇(Selection)、交叉(Crossover)和變異(Mutation)。遺傳算法的執行中有編碼操作和譯碼操作，其中編碼操作就是將表現型轉換到基因型，從基因型轉換到表現型被稱為譯碼操作。遺傳算法在進行分析的時候只是將一個種群看作是一個對象來對其進行分析，然后進行編碼、計算適應值、遺傳操作和篩選等步驟，這幾個方式都賦予了遺傳算法一定的優勢[3]。遺傳算法實現的基本流程見圖1。

1.2 程序設計流程

遺傳優化程序的基本流程見圖2。從圖2可知，通過船舶基本參數來確定散貨船的浮態和強度。為了滿足散貨船的約束條件，保證船舶在運營中的安全性，要對遺傳算法的參數進行限制。

1.3 遺傳編碼的確定

編碼是設計遺傳算法的一個關鍵步驟，編碼的好壞將直接影響到遺傳算法后面的選擇、交叉、變異等操作步驟。遺傳算法的一大難點就是選擇一個合適的編碼方案，針對一個具體的應用問題時，首要目標就是找到其編碼方案[4-5]。

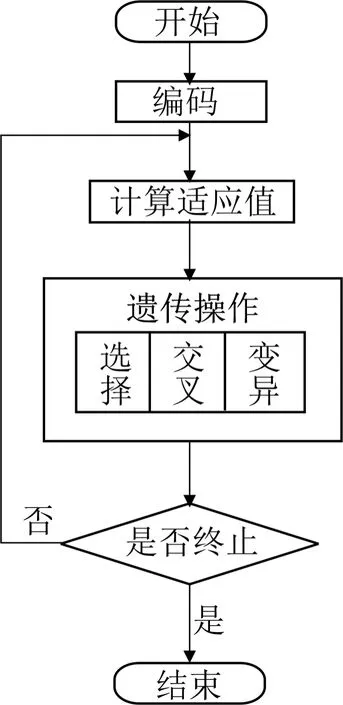
圖1 遺傳算法基本流程

Gen—遺傳的代次。

本文研究的76 000 t遠洋散貨船共有7個貨艙，本次遺傳算法優化采用兩輪裝貨的編碼方案。

隨機產生的初始解有可能出現強度或者穩性不合格的情況，為此對遺傳算法的初始解進行改進，可以采用第一輪裝入貨艙預計裝載量的1/2。

2 散貨船配載系統對約束條件的處理

基于遺傳算法的配載系統約束條件主要包括以下4點：

(1)艏艉吃水在散貨船裝貨過程中的任意狀態下都不允許超過裝貨港的限制。

(2)船舶吃水差在散貨船裝貨過程中的任意狀態下都要在限定范圍之內。

(3)各個校核點的剪力占該處剪力許用值的百分比不超許用值，且盡量小。

(4)初穩性滿足規范要求。

對于不滿足上述4個約束條件中任何一個條件的個體，裝載儀軟件中的約束條件函數會自動將其剔除出當前種群。

具體的操作步驟是：散貨船配載對種群進行適應度計算時，對上面的4個約束條件依次進行初始判斷，不符合的個體直接淘汰，并將其適應度f強制清零。符合的個體才依次進行其他操作，所以這些不能滿足約束條件要求的個體將無法被遺傳到下一代[6]。

2.1 適應度的縮放

遺傳算法中適應度對最終的優化結果有直接的影響，所以對適應度的選擇是極其重要的。一般遺傳算法的適應度是固定不變的，但是這樣存在著一些缺點。固定的適應度可能使早期種群中優秀的個體大部分都可以進入下一代，不僅會帶來早熟的現象，而且會使種群的多樣性受到影響，不能將早期較差個體中含有的部分優秀基因展示出來。這時，就需要采用適應度的縮放。早期適應度較低，能充分發揮每個個體中的基因作用；后期將適應度放大，擴大優秀個體之間的差異，從而能更好地得出最優解。

f′=af+b

(1)

式中：f′為縮放后的適應度;f為原來的適應度;a、b為系數。

2.2 模擬退火拉伸

Pau1 L.Stoffa提出了模擬退火拉伸。可以將此應用于遺傳算法當中，使遺傳算法具有適度的拉伸作用。

(2)

式中：fi為第i個的個體適應度；n為種群個數總數；g為遺傳代數序號；T為溫度；T0為初始溫度。

采用模擬退火拉伸，目的在于使早期的個體在溫度高時產生后代的概率相差不大，充分保障了種群的多樣性。當遺傳后期溫度下降后，拉伸作用將越來越明顯，使優秀的個體同普通個體拉開差距，從而獲得遺傳算法的優秀解[7]。

2.3 加入精英保留法

Grefenstette提出了精英保留策略。由于遺傳算法的包容性，可以在本次配載當中加入精英保留策略。遺傳算法中使用精英保留策略的主要目的就是為了使群體當中最優的個體不至于被淘汰，雖然最優的個體進化到下一種群的概率是很高的，但是以防萬一，最保險的就是將其直接復制到下一個種群當中，百分百概率保留，并將新種群當中隨機的一個種群個體或者最差的一個種群個體淘汰。這樣進行操作可以幫助遺傳算法優化的速度加快，并且保障了最優解的存在[8]。

3 軟件開發

結合上面理論知識，用C++語言在Windows環境下完成裝載儀在遺傳算法下進行貨物配載的開發工作。裝載儀編碼程序中構建遺傳算法的個體和種群兩個類，其中個體對應Individual，Generation對應種群。

(1)定義Individual類包括的成員變量和成員函數

設置個體染色體字符串、個體適應度和各艙第一輪的裝貨量的代碼和相應操作的代碼。

成員變量：Bool m_chrom[]

//個體染色體字符串

Float m_fitness

//個體適應度

Int m_xl～m_x7

//1～7輪的裝貨量

成員函數：Void Initial()

//初始化

Void GetX()

//解碼

Float Getiftness (int x1,int x2,int x3,int x4,

int x5,int x6,int x7)

//返回個體適應度

Void Update()

//更新

(2)定義Generation類包括的成員變量和成員函數

設置遺傳算法中父代種群、子代種群、種群中最優個體、最優個體的適應度、最優裝貨順序的代碼和相應操作的代碼。

成員變量：Individual m_oldpop[]

//父代種群

Individual m_newpop[]

//子代種群

Individual m_bestone

//最優個體

Float m_bestiftenss

//最優個體適應度

Floatm_bestsequenee[]

//最優裝貨順序

成員函數：VoidGeneration()

//構造函數

Int select

//選擇

Void Crossover(int ml,int m2)

//變異

Void Mutation(bool child[])

//遺傳

Void Generaiton()

//遺傳操作函數

散貨船配載軟件的系統流程圖見圖3。

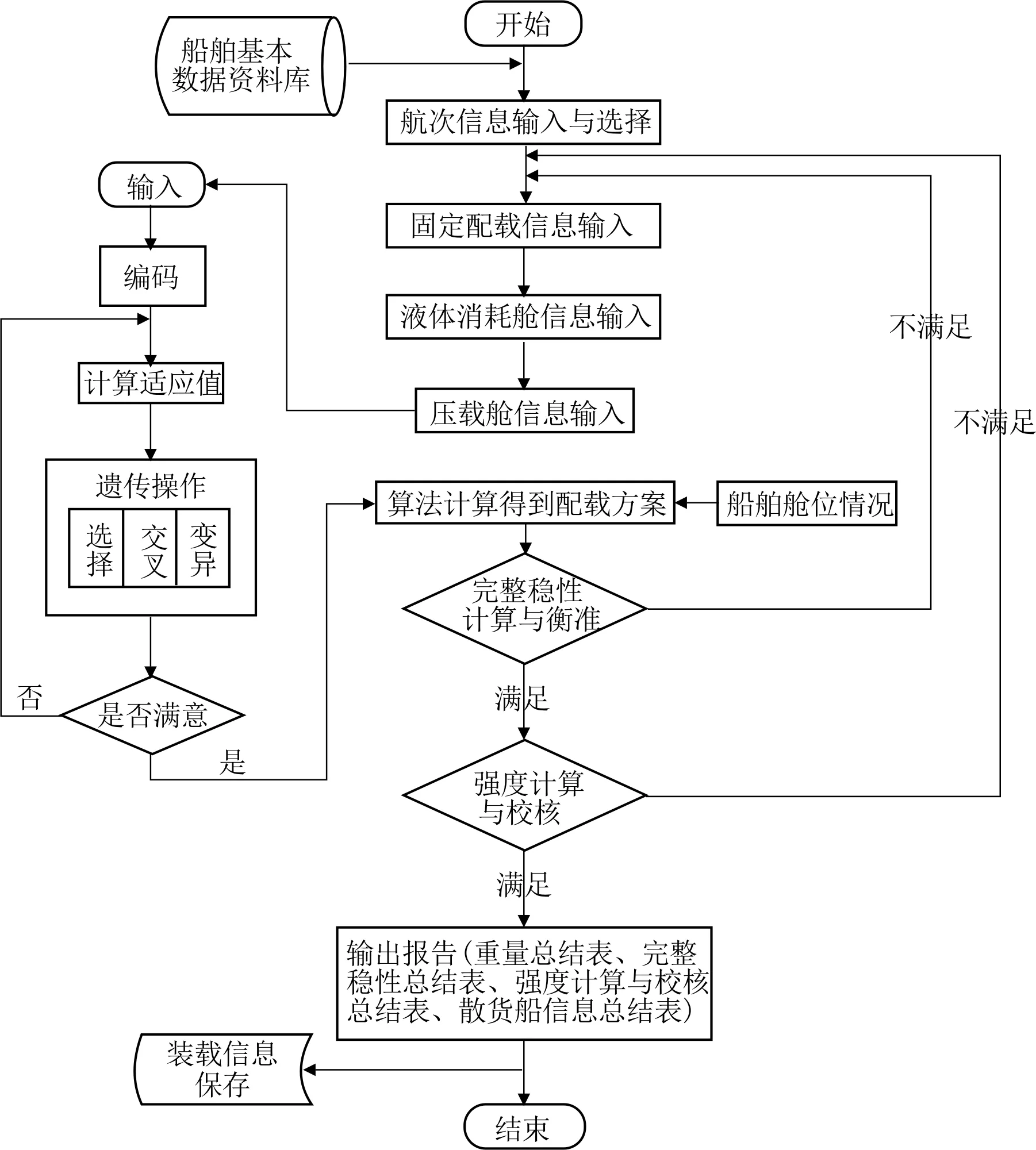
圖3 軟件流程圖

3.1 產生初始種群

利用計算機的隨機生成功能，連續隨機產生28位二進制數據，這個二進制數即是散貨船的一個初始個體。這個28位的二進制字符串對應個體的染色體，其中：1～4位對應的散貨船1號艙經過第一輪裝貨后的艙內貨物量，5～8位是對應散貨船2號艙經過第一輪裝貨后的艙內貨物量，以此類推。

初始種群是由初始個體組合而成的，可以用圖4來表示初始種群的生成過程。圖中:M為種群規模，字符串b=1000100010001000100010001000。

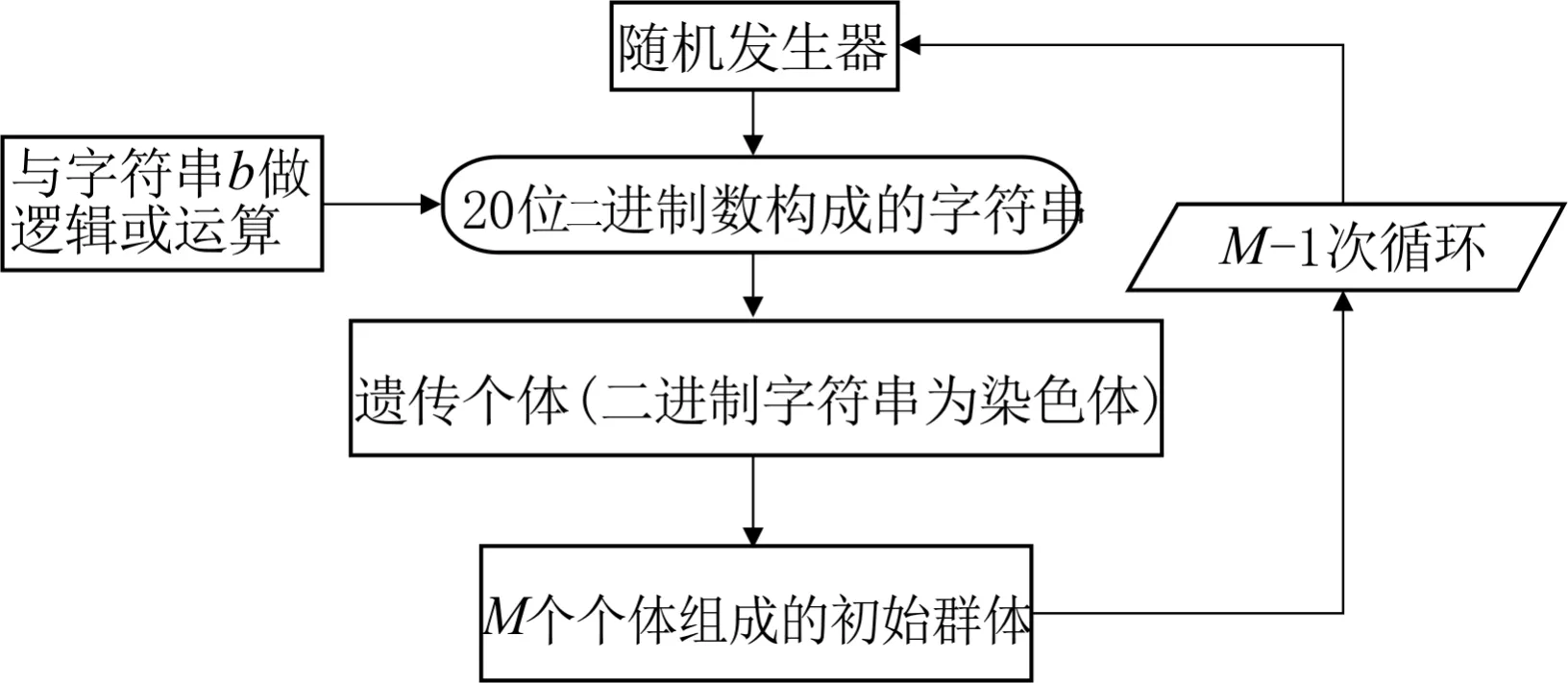
圖4 初始種群產生流程圖

本課題研究的是“76 000 t散貨船”，將散貨船的基本數據輸入裝載儀中，對遺傳算法的初始解進行改進，可以將總載貨量均勻分配作為初始解。1～7艙的裝貨量均為7 974.516,輸入裝載儀的貨艙裝載框中，見表1。表中：ρ為密度，Per為貨物所占艙室的體積比，W為貨物重量，H為貨物高度，LCG為重心縱向坐標。

裝載儀根據貨艙輸入框中的數據生成初始配載圖，具體內容見圖5，其中：X1～X7分別代表1～7艙的裝貨量。

計算散貨船在初始配載狀況下的船舶強度和穩性是否滿足要求。通過裝載儀算出“76 000 t散貨船”在改進初始配載下的強度和穩性。散貨船強度計算結果見圖6，穩性計算結果見圖7。

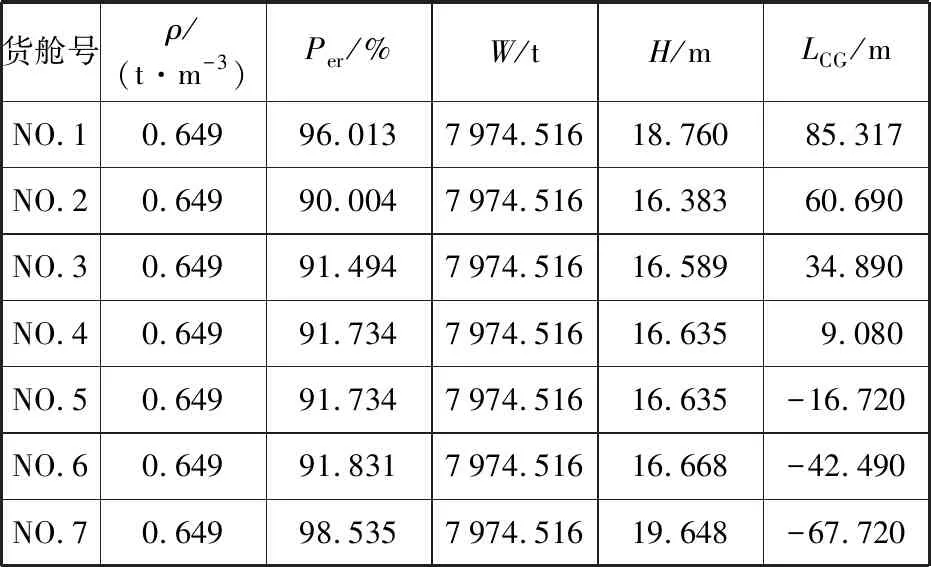
表1 初始解的貨艙輸入

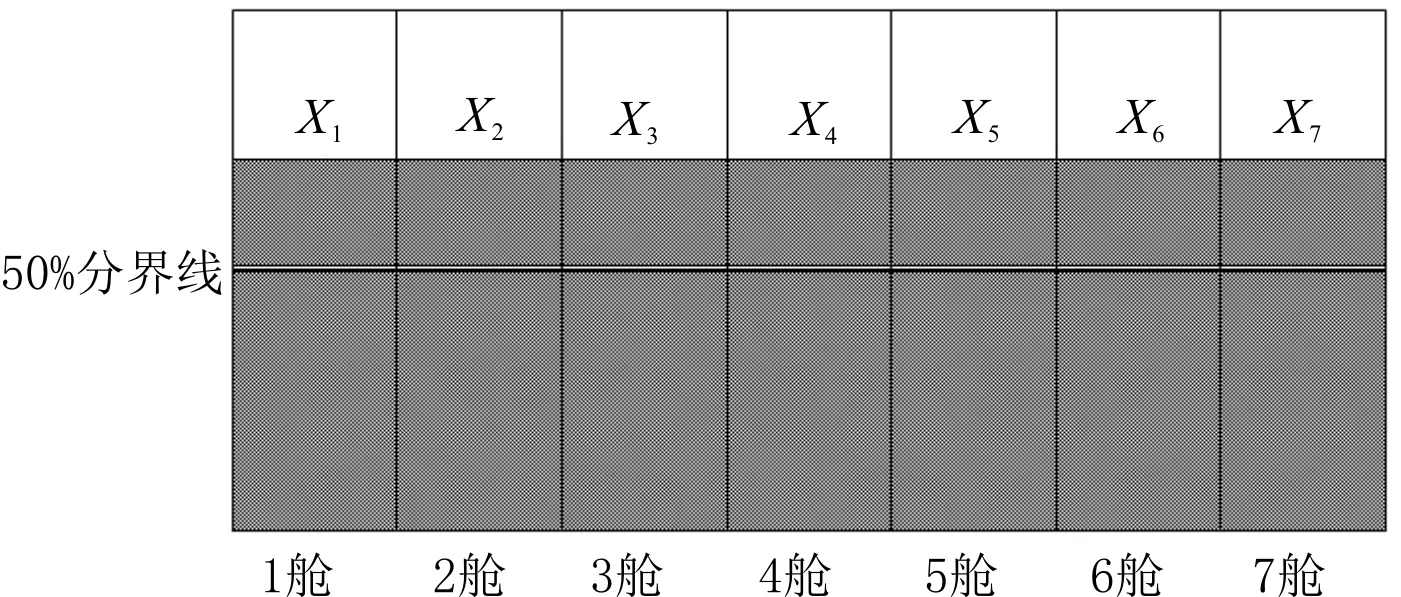
圖5 初始配載圖

圖6 初始解強度計算結果

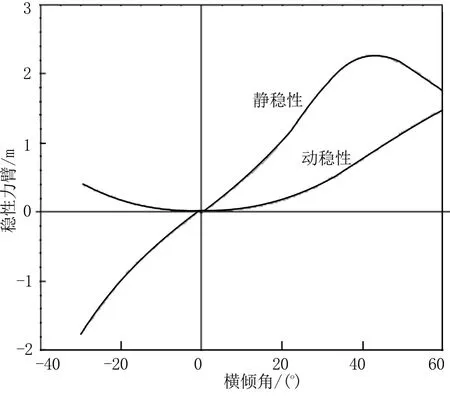
圖7 初始解穩性計算結果

3.2 遺傳算法的變異實現

經過初始裝配后，用代碼實現對個體的某些位置進行改變，將某些部位的二進制碼從1變成0或者從0變成1，形成新的種群個體。將船舶的初始配載量進行變異操作，得到變異后的1～7艙的裝貨量為7 216.393、8 610.586、7 310.325、8 010.546、7 410.546、6 408.331、7 644.128，然后將變異后的裝貨量輸入裝載儀中。裝載儀根據貨艙輸入框中的數據生成變異配載圖，見圖8，其中：X1～X7分別代表1～7艙的裝貨量。

計算散貨船在初始配載狀況下的船舶強度和穩性是否滿足要求。通過裝載儀算出“76 000 t散貨船”在變異配載下的強度和穩性。散貨船強度的計算結果見圖9，穩性計算結果見圖10。

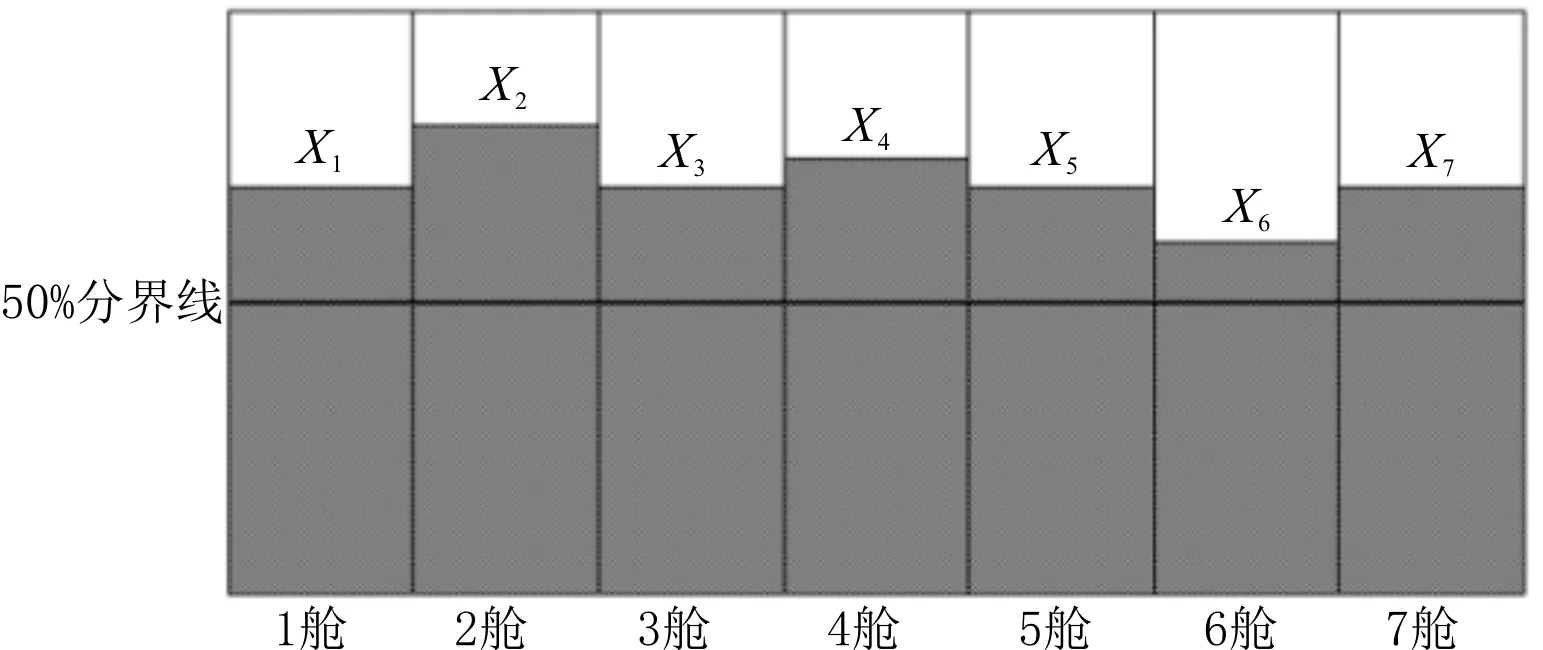
圖8 變異配載圖

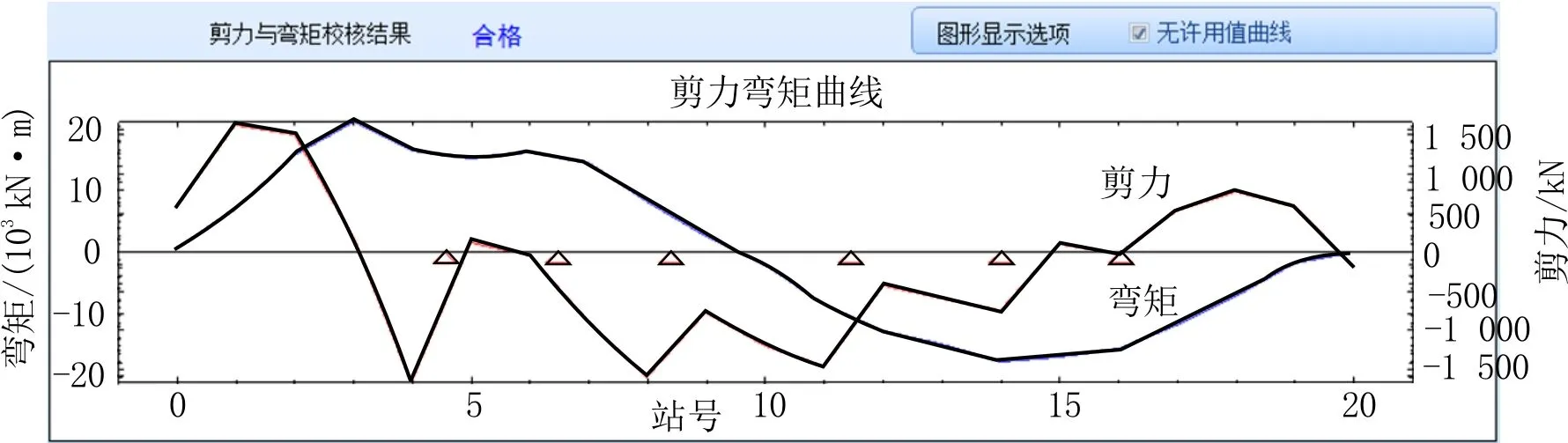
圖9 變異強度計算結果

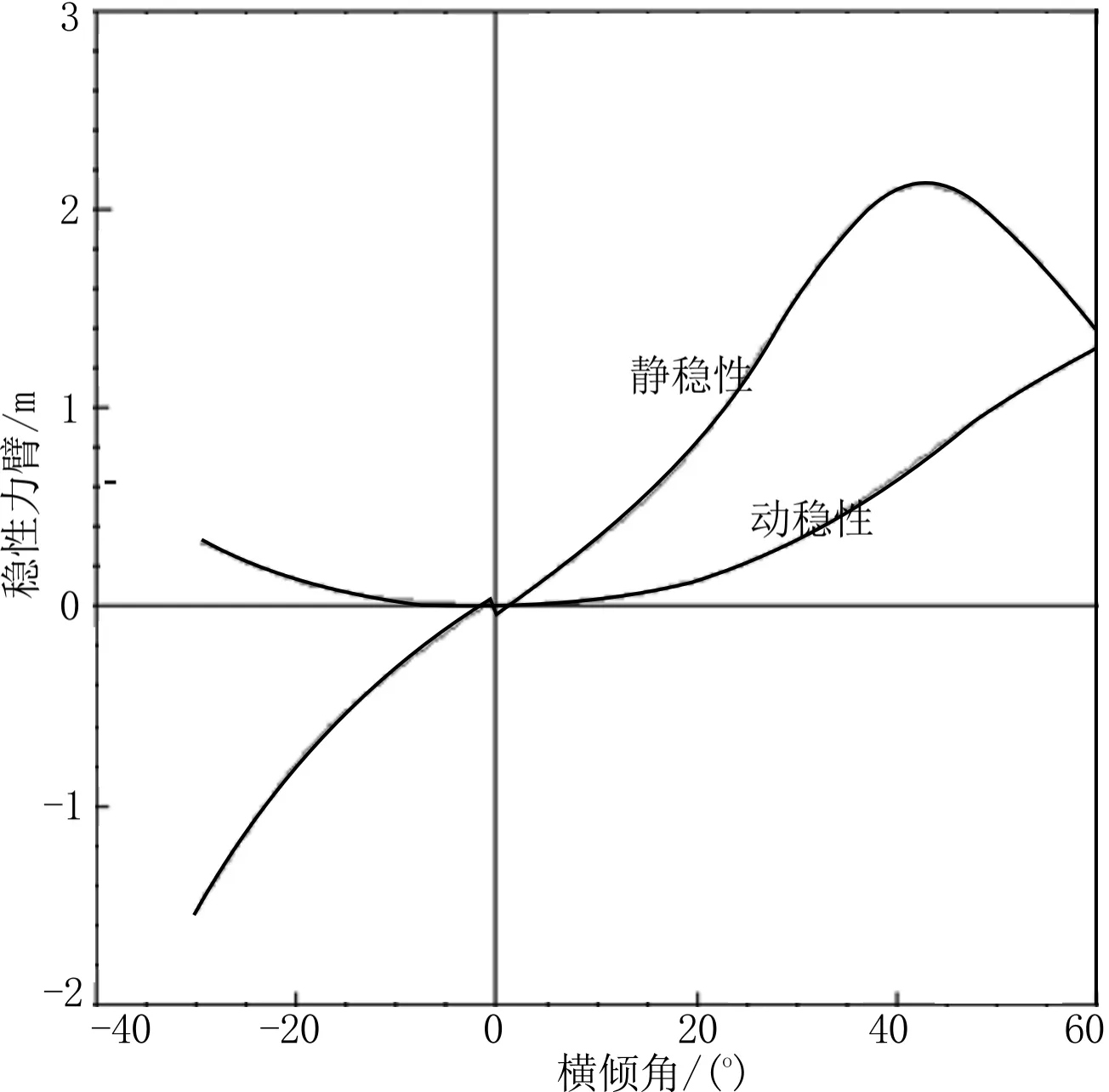
圖10 變異穩性計算結果

3.3 散貨船的最終配載完成

散貨船配載經過上面的變異操作后，接下來需要進行交叉算法實現。交叉算法的主要步驟是：

(1)找到散貨船配載交叉算法的起始點。

(2)對散貨船配載進行交叉操作。

(3)去除交叉之后的雷同信息。

經過初始裝配和變異裝配后，進行最后的交叉操作。通過計算機運算得到1～7艙的最優裝貨量，其裝貨量分別為8 040.393、7 500.558、7 927.325、8 710.546、7 422.546、6 906.331、8 244.128，將最優解裝貨量輸入裝載儀中。裝載儀根據貨艙輸入框中的數據生成變異配載圖，見圖11，其中：X1～X7分別代表1～7艙的裝貨量。

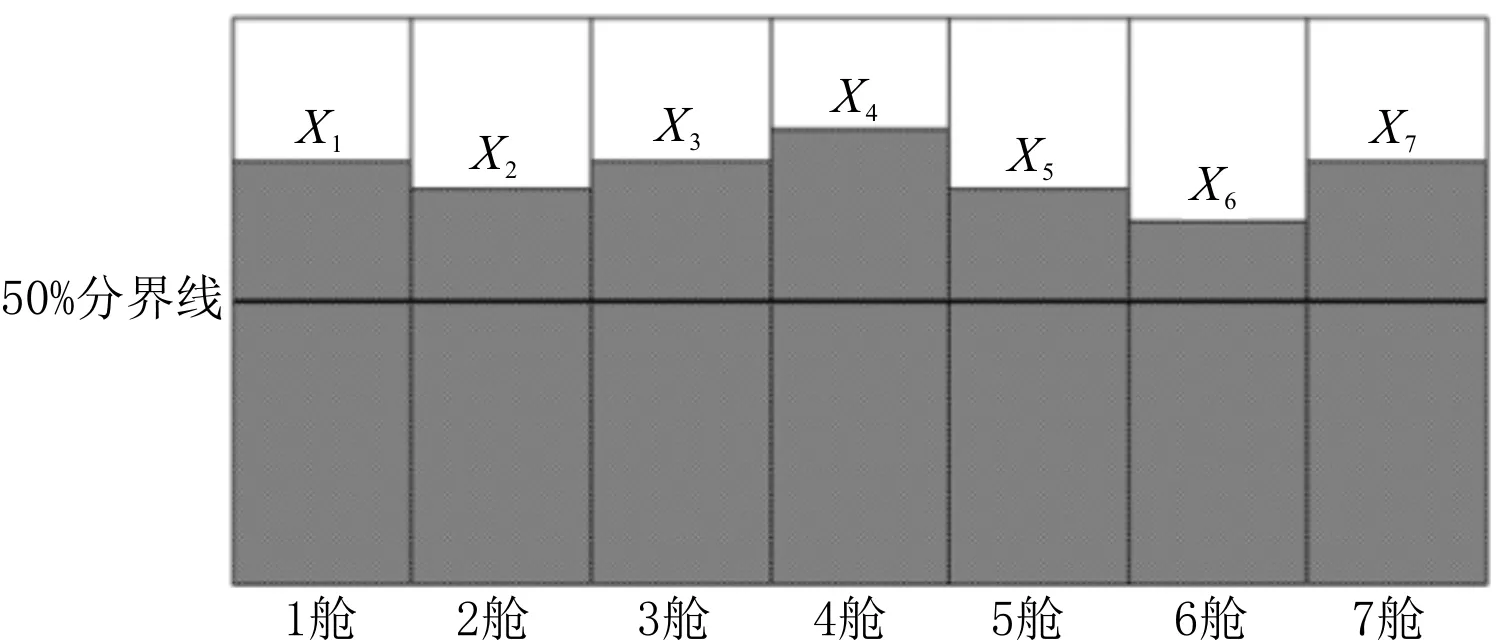
圖11 最優解配載圖

計算散貨船在初始配載狀況下的強度和穩性是否滿足要求。通過裝載儀算出“76 000 t散貨船”在最優解配載下的強度和穩性。散貨船強度計算結果見圖12，穩性計算結果見圖13。

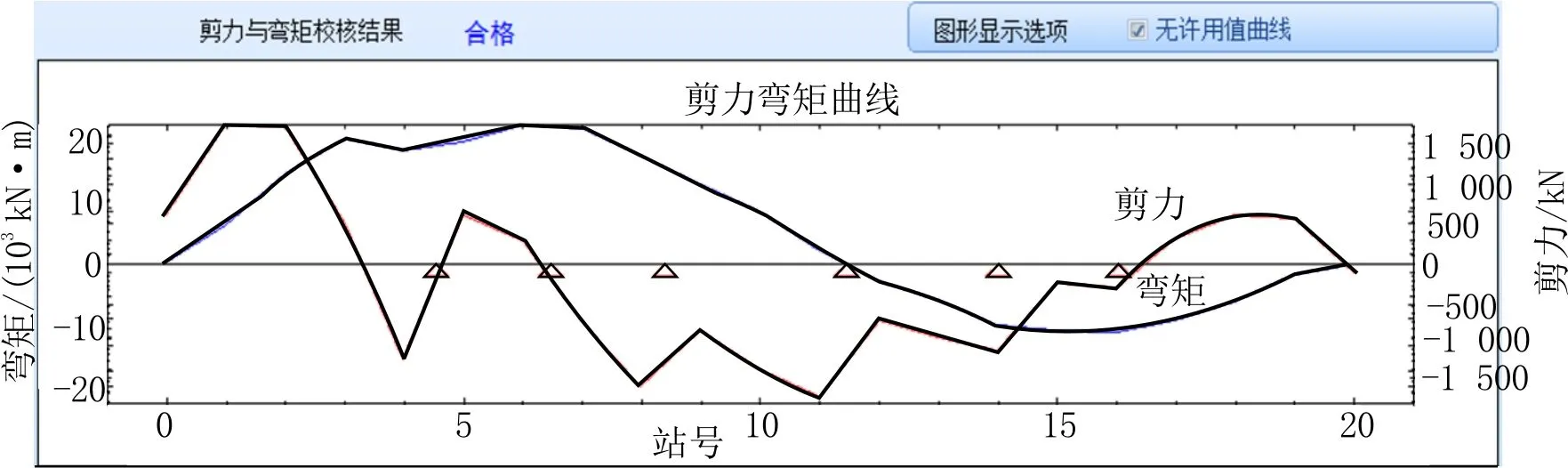
圖12 最優解強度計算結果

圖13 最優解穩性計算結果

從圖6、圖9、圖12中找出初始解、變異解、最優解的剪力許用值比例的最大值和彎矩許用值比例的最大值，其結果見表2。

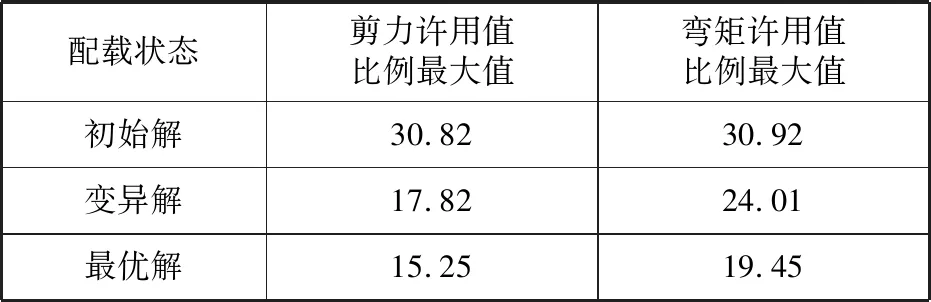
表2 強度計算結果對比

從表2看出，最優解下的剪力和彎矩許用值比例最大值表現最好，穩性沒有明顯的區別。經過遺傳算法優化后的船舶配載方案表現更好，所以此算法有得到滿意解的能力。

4 結語

散貨船優化配載問題是一個多目標組合優化問題，本文采用遺傳算法求解該問題。基于遺傳算法，嘗試求解在保證船舶安全航行的前提下，滿足船舶的強度和穩性的最佳方案，但是限于問題的復雜性，研究過程做了大量的假設，在實際應用中有一定的局限性。

如今，我國大多數散貨船碼頭仍然處于人工作業的狀態，需要配載人員做出大量的工作。因此，對散貨船配載的研究不管在理論還是實際上，都有著重要意義。