基于人工神經(jīng)網(wǎng)絡(luò)的線損計(jì)算及竊電分析

劉 超

（國(guó)網(wǎng)湖南省電力有限公司 婁底供電分公司，湖南 婁底 417000）

0 引 言

隨著我國(guó)經(jīng)濟(jì)的快速發(fā)展，電力需求不斷上升，但是隨著電力需求的快速增長(zhǎng)，配電網(wǎng)更加復(fù)雜，線損管理更加困難。雖然電力企業(yè)通過各種先進(jìn)技術(shù)手段和管理方式增強(qiáng)了電力監(jiān)管，但難以精準(zhǔn)響應(yīng)竊電行為，竊電情況時(shí)常發(fā)生，因此需要通過快速定位竊電位置進(jìn)行更精準(zhǔn)的管理。近些年，人工神經(jīng)網(wǎng)絡(luò)技術(shù)預(yù)測(cè)相應(yīng)算法在電力領(lǐng)域有了一定的發(fā)展，但現(xiàn)階段以神經(jīng)網(wǎng)絡(luò)為基礎(chǔ)的算法對(duì)具體的線損管理幫助有限，對(duì)特定區(qū)域范圍內(nèi)多個(gè)可能竊電位置的分析有所欠缺。因此，需建立有關(guān)地理區(qū)域的負(fù)荷和潮流分析模型，并利用竊電模型判定區(qū)域內(nèi)的線損情況和具體位置[1]。

1 人工神經(jīng)網(wǎng)絡(luò)原理以及模型的構(gòu)建

1.1 人工神經(jīng)網(wǎng)絡(luò)原理

人工神經(jīng)網(wǎng)絡(luò)就是通過模仿人神經(jīng)元的工作方式，在不同單元之間建立連接，形成以此為基礎(chǔ)的模型。人工神經(jīng)網(wǎng)絡(luò)主要包括輸入層、隱含層以及輸出層等結(jié)構(gòu)，如圖1所示。

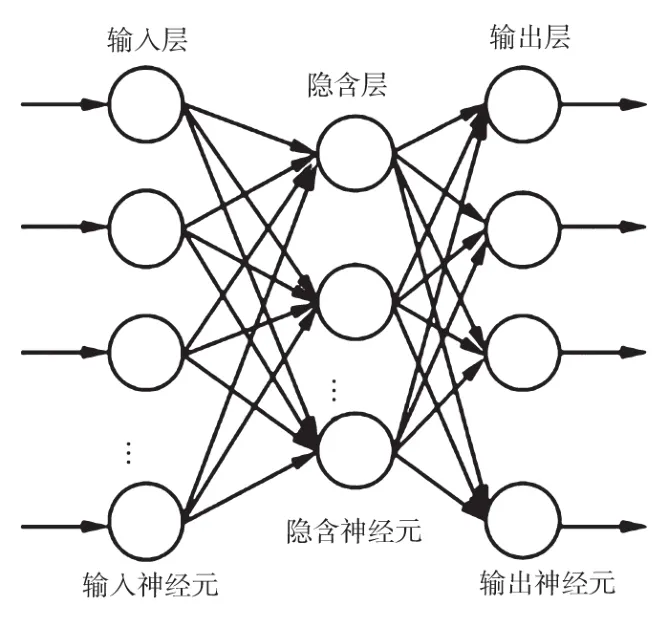
圖1 人工神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)模型示意圖

輸入信號(hào)通過兩層結(jié)構(gòu)激活函數(shù)后輸出，同時(shí)參照輸出誤差對(duì)每一層神經(jīng)元連接權(quán)值進(jìn)行調(diào)整，以不斷降低誤差，最終達(dá)到設(shè)定目標(biāo)。

1.2 計(jì)算及分析模型

為進(jìn)行線損計(jì)算和竊電分析，本文以人工神經(jīng)網(wǎng)絡(luò)為基礎(chǔ)建立配電網(wǎng)多潮流場(chǎng)景線損計(jì)算模型和區(qū)域性竊電位置判定模型，計(jì)算和分析的數(shù)據(jù)主要包括潮流、理論線損以及統(tǒng)計(jì)線損等。實(shí)際操作時(shí)，先分析原有數(shù)據(jù)，確定潮流、理論線損以及統(tǒng)計(jì)線損之間的關(guān)系，根據(jù)各節(jié)點(diǎn)負(fù)荷的輸入計(jì)算最終的統(tǒng)計(jì)線損值，然后在輸入接電負(fù)荷、統(tǒng)計(jì)線損以及理論線損的基礎(chǔ)上分析線損的重要因素比及是否存在竊電情況[2]。

理論線損是指電力傳輸過程中損耗的電能，利用均方根電流法和損耗因素法計(jì)算。將已有潮流數(shù)據(jù)作為人工神經(jīng)網(wǎng)絡(luò)模型的輸入，線損作為輸出，具體的理論線損計(jì)算為：

式中，St和Ss分別表示理論線損和統(tǒng)計(jì)線損；f表示神經(jīng)網(wǎng)絡(luò)訓(xùn)練所得線損計(jì)算函數(shù)；Pi和Qi分別表示第i個(gè)負(fù)載母線上的有功功率和無功功率；Pgi表示發(fā)電機(jī)發(fā)電功率。

2 樣本訓(xùn)練及竊電位置分析

2.1 樣本訓(xùn)練分析

人工神經(jīng)網(wǎng)絡(luò)模型的建立需要依靠大量可靠的訓(xùn)練數(shù)據(jù)，因此數(shù)據(jù)積累非常重要。在實(shí)際應(yīng)用過程中，配電網(wǎng)相應(yīng)位置設(shè)有可以采集數(shù)據(jù)的表計(jì)，樣本訓(xùn)練可以利用仿真來獲取數(shù)據(jù)。線損計(jì)算需要的數(shù)據(jù)主要是各個(gè)位置的有功負(fù)荷和無功負(fù)荷，實(shí)際應(yīng)用中標(biāo)記線損數(shù)據(jù)量相對(duì)較少，很難得到實(shí)時(shí)的線損數(shù)據(jù)，在此用IEEE14節(jié)點(diǎn)標(biāo)準(zhǔn)網(wǎng)絡(luò)實(shí)施仿真模擬[3]。

以典型潮流分布為基礎(chǔ)實(shí)施數(shù)據(jù)仿真，以獲取相對(duì)完整的仿真數(shù)據(jù)。仿真形式設(shè)定小范圍波動(dòng)（±10%）負(fù)荷300組，大范圍波動(dòng)（±50%）負(fù)荷300組，滿足每次切除1個(gè)負(fù)荷節(jié)點(diǎn)情況的負(fù)荷420組。在所有1 020組都完成輸入后，利用典型潮流計(jì)算方式獲取對(duì)應(yīng)的潮流輸出，得到對(duì)應(yīng)的1 020組數(shù)據(jù)[4]。這些數(shù)據(jù)中，人工神經(jīng)網(wǎng)絡(luò)的有效輸入量為22組，屬于算例中配電網(wǎng)的11個(gè)PQ節(jié)點(diǎn)的有功值和無功值，將這些數(shù)據(jù)當(dāng)成訓(xùn)練樣本來實(shí)施模型的訓(xùn)練。

2.2 竊電位置分析

通過遠(yuǎn)抄電量采集模塊將其與SQL Server 2000數(shù)據(jù)庫相連，比較分析數(shù)據(jù)庫中的理論線損計(jì)算相關(guān)數(shù)據(jù)與本系統(tǒng)計(jì)算所得的統(tǒng)計(jì)線損相關(guān)數(shù)據(jù)。在潮流模擬仿真時(shí)，選擇3、4、9、10、14這幾個(gè)典型節(jié)點(diǎn)為竊電節(jié)點(diǎn)，從上述數(shù)據(jù)中選定負(fù)荷波動(dòng)在±20%范圍內(nèi)的3 000組潮流數(shù)據(jù)和線損值，同時(shí)設(shè)定沒有出現(xiàn)竊電情況，不考慮表計(jì)故障等外部因素影響的情況下，理論線損值就是統(tǒng)計(jì)線損值。將3 000組數(shù)據(jù)分為5類進(jìn)行竊電分析，表計(jì)值隨著竊電的發(fā)生也會(huì)有所下降，但是因?yàn)閷?shí)際用量沒有發(fā)生改變，所以統(tǒng)計(jì)線路也沒有產(chǎn)生變化。此種情況下能夠獲取3 000組負(fù)荷相應(yīng)的理論線損及統(tǒng)計(jì)線損，并且將潮流情況與線損值當(dāng)成輸入，將竊電的產(chǎn)生和作為當(dāng)成輸出，建立竊電分析模型[5]。為保證訓(xùn)練的成果，除了獲取訓(xùn)練樣本外還要設(shè)置測(cè)試樣本，如表1所示。

表1 測(cè)試樣本設(shè)置情況

2.3 神經(jīng)網(wǎng)絡(luò)訓(xùn)練模型設(shè)置

神經(jīng)網(wǎng)絡(luò)參數(shù)調(diào)節(jié)是提升計(jì)算準(zhǔn)確性和效率的核心，為有效提高訓(xùn)練效率，實(shí)施數(shù)據(jù)的歸一化處理，控制數(shù)值在[-1,1]，歸一化函數(shù)設(shè)定為：

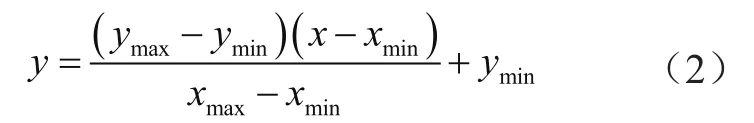
式中，y表示歸一后的數(shù)值；x表示原始值；ymax和ymin分別為1和-1。

確定好歸一函數(shù)后要設(shè)定神經(jīng)網(wǎng)絡(luò)節(jié)點(diǎn)，可以采用雙隱含層的方式進(jìn)一步提升準(zhǔn)確性，節(jié)點(diǎn)數(shù)分別設(shè)置為11、10。采取梯度下降算法設(shè)定訓(xùn)練函數(shù)，具體形式為：

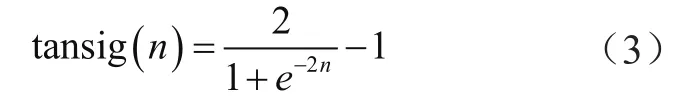
式中，n表示前一神經(jīng)元傳遞輸入值，范圍控制在（-1,1）。將迭代次數(shù)設(shè)置為10 000，精度設(shè)置為0.01%，學(xué)習(xí)步長(zhǎng)為0.1，考慮檢驗(yàn)的有效性，在兩次迭代偏差小于設(shè)定值或者偏差擴(kuò)大時(shí)要自動(dòng)停止迭代[6]。

3 算例的結(jié)果和具體分析

3.1 線損計(jì)算結(jié)果分析

對(duì)潮流模擬所得的1 020組結(jié)果，根據(jù)不同類別隨機(jī)選擇相應(yīng)的測(cè)試樣本，包括低負(fù)荷波動(dòng)20組、高負(fù)荷波動(dòng)20組以及滿足切除情況28組。將其他樣本當(dāng)成訓(xùn)練樣本實(shí)施模型訓(xùn)練，得到神經(jīng)網(wǎng)絡(luò)訓(xùn)練線損計(jì)算模型收斂結(jié)果如圖2所示，理論線損和實(shí)際線損的誤差如圖3所示[7,8]。

圖2 神經(jīng)網(wǎng)絡(luò)訓(xùn)練線損計(jì)算模型收斂結(jié)果

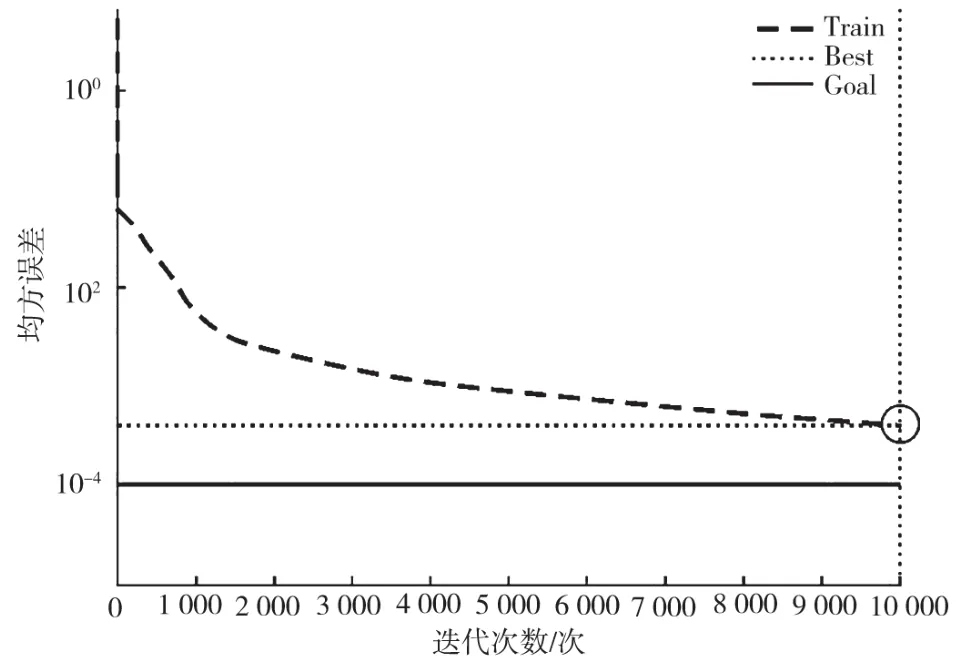
圖3 理論線損和實(shí)際線損的誤差

3.2 竊電位置分析

梯度下降算法下竊電位置分析的結(jié)果如表2所示，訓(xùn)練樣本相同的情況下可以達(dá)到比較高的準(zhǔn)確率。

表2 竊電位置分析結(jié)果

隨著竊電節(jié)點(diǎn)數(shù)量的上升，模型無法有效識(shí)別竊電量下降。神經(jīng)網(wǎng)絡(luò)模型對(duì)于泛化能力的要求較高，傳統(tǒng)梯度下降學(xué)習(xí)算法無法滿足，因此要對(duì)其進(jìn)行優(yōu)化。

列文伯格-馬夸爾特法是目前普遍應(yīng)用的非線性最小二乘算法，可獲取最小化非線性數(shù)值解。其使用Keras庫建立神經(jīng)網(wǎng)絡(luò)模型，設(shè)定KM神經(jīng)網(wǎng)絡(luò)的輸入節(jié)點(diǎn)數(shù)為3，輸出節(jié)點(diǎn)為1，隱藏節(jié)點(diǎn)數(shù)為10，使用Adam方法求解，隱藏層使用ReLU(x)=(0,x)為激活函數(shù)，通過修改參數(shù)來獲取梯度下降法和高斯-牛頓算法的優(yōu)點(diǎn)。列文伯格-馬夸爾特法具有較快的收斂速度和較強(qiáng)的泛化性，但每次迭代需要消耗較長(zhǎng)時(shí)間并且內(nèi)存占比較大[9]。

相較于梯度下降算法，采用列文伯格-馬夸爾特法能有效提升多竊電位置識(shí)別的準(zhǔn)確性和模型泛化識(shí)別能力[10]。由于訓(xùn)練的樣本相對(duì)單一，對(duì)不同的竊電比率缺少識(shí)別敏感度，因此在無竊電和低比率竊電的情況下還是很難識(shí)別竊電位置。為提升識(shí)別準(zhǔn)確性，增加無竊電500組以及各節(jié)點(diǎn)5%竊電數(shù)據(jù)共3 000組后再次實(shí)施神經(jīng)網(wǎng)絡(luò)訓(xùn)練，發(fā)現(xiàn)增加訓(xùn)練樣本后無竊電和低比率竊電識(shí)別效果較好[11]。

4 結(jié) 論

本文主要以人工神經(jīng)網(wǎng)絡(luò)理論為基礎(chǔ)建立了理論線損模型，并對(duì)線損計(jì)算和竊電位置進(jìn)行了分析，轉(zhuǎn)變了傳統(tǒng)理論驅(qū)動(dòng)線損的計(jì)算方式，具有實(shí)際意義。