基于VaR模型的商業銀行利率風險度量與管理

羅熙茗 付湘山

[摘 要]隨著我國利率市場化的逐漸深入，利率風險增加了商業銀行經營的不確定性，嚴重時甚至會導致系統性風險。為了度量商業銀行的利率風險，倫敦銀行間同業拆借利率（LIBOR）為研究對象，選取了2009年1月2日至2019年7月10日的隔夜拆借利率，使用VaR模型對其存在的利率風險進行了分析和研究。結果表明，對于商業銀行的隔夜拆借利率敏感型業務而言，在90%、95%、99%置信度下的最大損失（風險）分別為資產市場價值的43.92%、50.36和58.43%，可見商業銀行面臨的利率風險很大。建議建立存款保險制度用以對沖利率風險，增強商業銀行運營的穩定性。

[關鍵詞]利率風險;VaR模型;風險管理;倫敦銀行間同業拆借利率

[中圖分類號] F83? ? ? ? ? ?[文獻標識碼] A? ? ? ? [文章編號] 2095-3283（2020）03-0064-05

Measurement and Management of Interest Rate Risk of Commercial Banks

—Based on Var Model of a Case Study of Libor

Luo Ximing? ?Fu Xiangshang

（School of Economics and Management China University of Geosciences， Beijing 100083）

Abstract： With the gradual deepening of interest rate liberalization in China， interest rate risk increases the uncertainty of commercial Banks' operation， and even leads to systematic risk in serious cases. In order to measure the interest rate risk of commercial Banks， this paper takes LIBOR as the research object， selects the overnight lending rate on January 2， 2009 solstice and July 10， 2019， and USES the VaR model to analyze and study its interest rate risk. The results show that the maximum loss （risk） in the case of the overnight lending rate sensitive business of commercial Banks under the confidence of 90%， 95% and 99% is 43.92%， 50.36 and 58.43% of the market value of assets respectively， indicating that commercial Banks are faced with great interest rate risk. Therefore， this paper proposes to establish a deposit insurance system to hedge interest rate risks and enhance the stability of commercial Banks.

Key Words： Interest Rate Risk; Commercial Banks; Var Model; Libor

一、引言

利率風險是指利率波動使得商業銀行的實際收益與預期收益發生一定程度的偏差，進而使得商業銀行遭受損失的一種不確定性。隨著世界各國利率市場化邁入新征程，如何有效地識別、量化和管理利率風險，成為保證商業銀行健康穩定發展的重要問題。自2018年5月30日銀保監會發布《商業銀行銀行賬簿利率風險管理指引》以來，我國銀行業的風險管理架構不斷完善，風險偏好與限額管理趨于精準，風險管理策略有效性逐步提高。

LIBOR即倫敦同業拆借利率，是在倫敦銀行內部交易市場上的商業銀行對存于非美國銀行的美元進行交易時所涉及的利率。LIBOR常常作為商業貸款、抵押、發行債務利率的基準。同時，浮動利率的長期貸款利率也會在LIBOR的基礎上確定。LIBOR同時也是很多合同的參考利率。結合LIBOR近年來的實踐運行情況可發現，LIBOR在理論上和實踐上存在合理性與可操作性，可以及時并準確地反映當前資金供給與需求變化，并且在將來能夠作為連接金融市場和金融體系的各個機構之間的紐帶，擔任未來各國貨幣政策調控體系主要政策工具的基準利率。

二、文獻綜述

（一）利率風險方面的研究

劉松林、朱霞（2010）使用了由 Duffee 建立的回歸方程，經過計算他們得出利率風險與信用風險兩者之間存在著負相關關系，作為進行風險管理的部門必須強化相關管理制度的建設，進一步提升利率風險的計量水平和利率風險的管理水平，而不能只考慮一種類型的風險。姚遠（2011）選擇七家上市銀行，以2006年至2007年的數據為樣本，應用利率敏感性缺口模型進行實證研究，著重考察利率敏感性缺口、缺口率、利率敏感性比率、偏離這四個指標，得出結論：商業銀行一年期以上資產、負債期限不匹配，長期利率風險凸顯，并提出可以通過調整資產負債結構來增強長期資產和負債的匹配度。謝曉雪（2012）總結了商業銀行利率風險管理面臨的挑戰，指出提高自主定價水平和風險定價能力是實現有效利率風險管理的關鍵。向陽（2013）強調基于利率市場化的前提，商業銀行在進行風險管理時應該充分利用利率衍生產品，高效管理利率市場風險。王晉忠、高菲（2015）應用最小方差以及套期保值等模型，通過對比分析的方法，分別研究利率衍生工具在對沖風險過程中的作用，闡明利率風險管理效果較好的方法為把利率互換和國債期貨的動態模型與最小方差模型相結合。王清、邱靜和劉雨露（2015）以工商銀行為例，運用缺口模型實證分析，指出現階段我國商業銀行利率風險管理意識淡薄，利率風險管理手段落后，需進一步加強。

（二）VaR模型在利率風險度量中的運用

趙敬（2012）通過VaR模型的基本原理和具體操作方法對我國的利率風險度量指標體系進行了評估，得出了GED分布下的GARCH（1，1）模型能較好地描述我國商業銀行所面臨的利率風險狀況等結論。王勇飛（2012）使用了風險價值VaR模型對銀行間市場債券質押式回購利率風險進行測度，從而對利率風險進行有效評估，得出了商業銀行對其他風險運用VaR模型進行度量的時候應根據不同的樣本選擇不同的GARCH模型進行計算，我國商業銀行必須加快對VaR模型的應用研究，提高銀行利率風險的管理能力等結論（王勇飛，2012）。徐靈（2013）使用了VaR方法中的方差—協方差法與歷史模擬法對我國商業銀行利率的風險管理和度量進行了評估，得出了商業銀行需要建立全面的數據信息系統，并選擇適當的置信水平和持有期長度，以便于結合VaR方法中的方差—協方差法與歷史模擬法，同時配合壓力測試及后測檢驗，從而更好地預防極端風險對商業銀行造成的影響這一結論。何堤（2013）通過VaR模型和GARCH模型對上海銀行間同業拆借利率進行風險度量研究，得出了SHIBOR 價格收益率序列波動在很大程度上依賴過去的價格波動和誤差，上海同業拆放利率市場價格波動風險可由過去的價格風險進行預測。李艷珍等（2016）運用GARCH族模型模擬市場利率變動和VaR模型度量商業銀行利率風險，得出了我國商業銀行短期利率風險較大，我國銀行間同業拆借利率序列不存在顯著的杠桿效應等結論。

三、模型與數據

隨著我國逐步推進利率市場化，利率風險管理也顯得越來越重要，學者對這一部分的研究愈加重視。基于前人的研究，本文采用倫敦同業拆借利率數據，運用VaR模型對商業銀行所面臨的利率風險進行了測算和分析，對存在的問題提出了相關政策建議。

（一）VaR模型簡介

VaR（Value at Risk）即處于風險中的價值，一般被稱為風險價值或在險價值，是指在市場正常波動下，某一金融資產或證券組合的最大可能損失（何堤，2013）。VaR方法將銀行的全部資產組合風險概括為一個簡單的數字，并以美元計量單位來表示風險管理的核心——潛在虧損。這也正是VaR能夠成為全行業衡量風險的一個方法標準的原因。VaR通常可以表示為：

Prob（△P>VaR）=1-α? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （1）

其中：Prob為概率，ΔP為資產組合的最大可能損失，α為置信水平，VaR表示置信度為α的風險價值。由此可知，置信水平的高低和持有期的長短是影響VaR值的兩個重要參數。

（二）數據選取與分析

本文選取倫敦同業拆借利率（LIBOR）的隔夜數據作為VaR模型實證的對象。LIBOR是倫敦的第一流銀行之間短期資金借貸的利率，是國際金融市場大多數浮動利率的基礎利率。該利率一般分為兩個利率，即貸款利率和存款利率，兩者之間的差額為銀行利潤。通常報出的利率為隔夜（兩個工作日）、7天、1個月、3個月、6個月和1年期。而隔夜利率在銀行間的使用頻率相對較高，因此本文選取2009—2019年共2253個隔夜（O/N）倫敦同業拆借利率為樣本，研究商業銀行的利率風險，數據來源為和訊網（http：//www.hexun.com）。

四、結果與討論

（一）平穩性分析

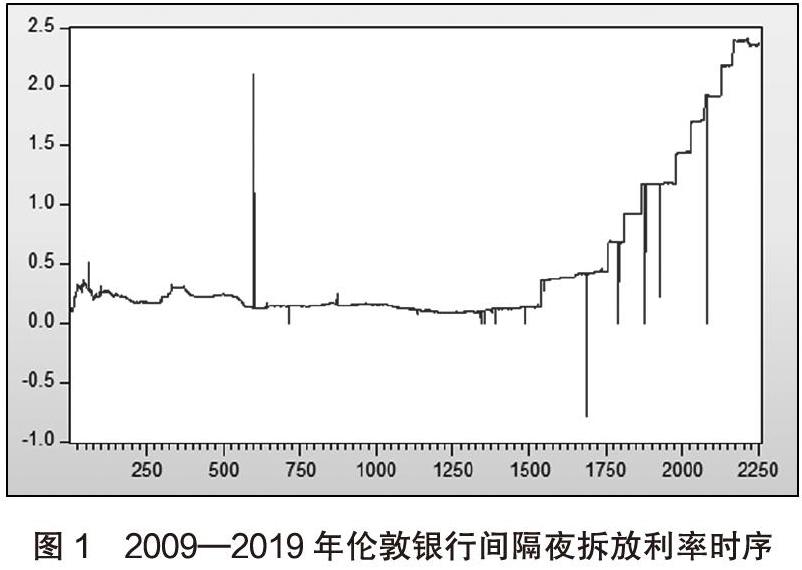
為了能夠使用GARCH族模型，對2009—2019年的倫敦銀行間同業拆借美元利率進行擬合，必須要保證該金融時間序列的穩定性。而檢驗LIBOR時間序列平穩性的直觀方法，是繪制其時序圖。2009—2019年倫敦銀行間隔夜拆放利率時序圖如圖1所示（由于部分日期數據缺失，共收集到有效數據2253個）。

由圖1可以看出，LIBOR利率具有較大的不穩定性。若直接用其進行建模分析，會產生嚴重的自相關性以及波動性的問題。由此，為了得到比較平穩的隔夜LIBOR收益率的時間序列數據，本文對所有收集到的隔夜LIBOR收益率進行對數差分處理，得到的結果記為r。計算公式如下：

rt=ln（LIBORt）-ln（LIBORt-1）? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （2）

上式中，rt為第t日隔夜LIBOR收益率的對數差分收益率。ln（LIBORt）和ln（LIBORt-1）分別為第t日和第t-1日的隔夜LIBOR 收益率。后文稱由rt構成的時間序列為收益率序列。

為了進一步驗證收益率序列具有平穩性，下面進行單位根檢驗（augmented dickey-fuller test）。單位根檢驗是指，檢驗系列中是否存在單位根過程。可以證明，若序列中存在單位根過程，則該序列必然不平穩，由此將導致回歸分析中出現偽回歸。用Eviews10軟件對收益率序列做單位根檢驗，結果如圖2所示。

由圖2可知，ADF檢驗所得的t統計量值小于顯著性水平為1%、5%和10%給出的參考值。因此可以得出結論：收益率序列不存在單位根過程，具有較好穩定性。

（二）自相關檢驗

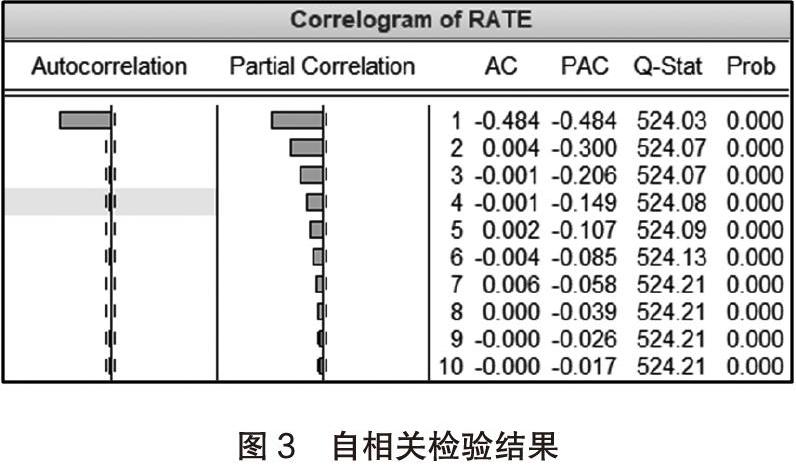
大量實證研究表明，由于經濟行為的滯后性，經濟變量的慣性，其他隨機偶然因素的影響，觀測數據的處理等因素，金融時間序列數據常常表現出顯著的時間慣性特點，即時間序列的不同時點上的數據存在某種程度的相互關聯性。如果不考慮數據的自相關性，將會導致模型預測失效，顯著性檢驗失效以及參數估計無效等問題。所以，本文在構建GARCH族模型之前對收益率序列進行自相關檢驗。各個滯后期自相關和偏相關系數如圖3所示。

由圖3可知，收益率序列r的自相關系數AC與偏相關系數PAC不全為零，證明LIBOR收益率序列存在一定的自相關性。但其滯后2期的自相關系數AC值為0.004，滯后10期的自相關系數AC值為0.000，可見其自相關程度較低。

（三）條件異方差檢驗

由圖1可以直觀看出，隔夜LIBOR收益率序列在不同時間段內波動幅度也不同。前半段收益率波動較為平緩，后半段收益率波動有所加劇。這意味著LIBOR收益率樣本數據可能存在異方差，有待條件異方差檢驗。

具體的檢驗方法是，運用自回歸條件異方差模型，簡稱ARCH模型（Autoregressive heteroskedasticity model）。該模型將當前所有可得的信息作為已知前提，進而運用自回歸的方式來描述數據序列方差的變化及其特征。首先運用最小二乘法對2252個隔夜LIBOR數據序列構建一階自回歸。進而用Eviews10軟件對收益率進行之后一階的ARCH-LM檢驗，定量地判斷收益率序列是否存在ARCH效應。檢驗結果如圖4所示。

從ARCH-LM檢驗結果來看，在95%的置信度水平下，F統計量等于736.2328，相伴概率為0.0000;Obs*R-squared統計值等于553.7367，相伴概率等于0.0000。兩個相伴概率均小于其臨界值，應當拒絕原假設而接受備擇假設，即隔夜LIBOR收益率序列的殘差在上述條件下存在顯著的ARCH效應。

由此，本文采用GARCH族模型對收益率數據序列進行擬合，根據已有實證研究的經驗，p=1或2，q=1或2可以較好地刻畫金融時間序列。運用Eviews10軟件分別檢驗分析N-GARCH（1，1）、N-GARCH（1，2）、N-GARCH（2，1）、N-GARCH（2，2），結果如表1所示。

運用Eviews10軟件分別檢驗分析GED-GARCH（1，1）、GED-GARCH（1，2）、GED-GARCH（2，1）、GED-GARCH（2，2），結果如表2所示。

運用Eviews10軟件分別檢驗分析t-GARCH（1，1）、t-GARCH（1，2）、t-GARCH（2，1）、t-GARCH（2，2），結果如表3所示。

上述結果表明，所有GARCH族模型均通過了顯著性檢驗，同時GED-GARCH（1，2）模型的AIC值和SC值最小。根據日本統計學家赤池弘次創立的AIC信息準則（Akaike Information Criterion）以及SC準則（Schwarz Criterion），通過比較不同分布滯后項的模型擬合優度，以確定合適的滯后期長度。具體操作時，在目標模型中不斷增加滯后變量，直到AIC值和SC值都不再降低為止。換句話說，AC和SC值越小表明模型的擬合程度越好。由此，本文選擇GED-GARCH（1，2）模型對收益率數據序列進行擬合，計算結果如圖5所示。

（四）VaR計算

首先，本文根據收益率數據序列擬合GED-GARCH（1，2）方程。接著，利用Eviews10軟件的GARCH估計模塊得出收益率序列r的一步向前預測條件均值和方差。最后，利用在VaR的定義式，得出不同置信度下的VaR測算值。具體公式如下：

本文將頭寸設為1個單位，進而測算了自由度為9.314714的GED（廣義誤差分布）在90%、95%和99%置信水平下的分位數。將其與各置信度下的條件均值、條件標準差以及VaR計算結果整理如表4所示。

由上述VaR的計算結果可知：對于商業銀行的隔夜拆借利率敏感型業務而言，在90%的置信度下的最大損失（風險）為資產市場價值的43.92%;在95%的置信度下的最大損失（風險）為資產市場價值的50.36%;在95%的置信度下的最大損失（風險）為資產市場價值的58.43%。由此可見，世界各地的商業銀行都應該充分重視利率風險的實時監測及管理。

五、結論與對策建議

（一）研究結論

本文選用2009—2019年倫敦銀行間同業拆借利率的隔夜（O/N）數據進行了實證研究，收益率數據的樣本容量為2253個。在實證過程中，首先對隔夜LIBOR收益率進行對數差分處理，得到較為穩定的時間序列。進一步，運用Eviews10軟件對2253個樣本數據從平穩程度、是否存在自相關性和是否存在條件異方差性三個方面進行檢驗。可以得出以下結論：

第一，收益率序列具有弱平穩的條件。第二，收益率序列存在較低程度的一階自相關特性，模型的擬合效果較好。第三，由ARCH-LM檢驗結果可知，收益率序列存在條件異方差，即收益率序列的殘差序列存在顯著的ARCH效應，可以用GARCH族模型進行擬合。

經過比對不同GARCH族模型的擬合效果，根據AIC信息準則以及SC準則，本文發現：GED-GARCH（1，2）模型對收益率數據序列的擬合效果最佳。據此擬合方程，本文測算了不同置信度下的VaR數值。結果表明：對于商業銀行的隔夜拆借利率敏感型業務而言，在90%、95%、99%置信度下的最大損失（風險）分別為資產市場價值的43.92%、50.36和58.43%。因此，本文得出“商業銀行的利率風險較大，對利率風險的實時監測和管理十分必要”的結論。

（二）對策建議

1.建立存款保險制度

存款保險制度的必要性在于它為存款提供了繼商業銀行之后的第二道屏障，當銀行無力償還存款時，保險公司將代為償還，這樣既可使存款人的安全性大大增加，同時增加了銀行的信用，也起到了穩定金融體系的作用。審慎監管制度、最后貸款人制度和存款保險制度構成了維護金融安全的三道防線。

2.利率與匯率改革雙管齊下

利率和匯率是市場經濟下進行投資的風向標，也是我國宏觀調控的主要工具。推動金融市場改革，尤其是利率和匯率市場化雙管齊下，可增強市場在經濟中的資源配置作用，增強配置效率，促進經濟機構的調整與整體發展。而且，二者必須齊頭并進，相互補充。相對應的，利率是貨幣價格的國內指標，匯率是貨幣價格的對外指標。同樣，內外指標形成、運行必須協調一致，整體經濟才可以實現穩定發展。

3.完善金融監管機制

利率市場化是我國金融體系改革中極為關鍵的一部分，它的順利推進對我國經濟發展起到深遠影響，但也需要相關金融環境給予適當和必要的支撐，尤其是來自中央銀行的監督和支持。利率市場化改革后，央行不能直接確定商業銀行的存貸款利率，只能通過公開市場操作，借助市場機制傳導，間接對利率水平進行引導和影響。所以，上述傳導機制應在利率市場化改革前就建立和完善。這樣，在面臨改革過程中的一些突發情況時，可通過完善的機制進行相應的反應。

[參考文獻]

[1]何堤.上海銀行間同業拆借利率的風險度量研究——基于GARCH族模型及VaR方法[D].昆明：云南師范大學，2013：61-65.

[2]李艷珍，李莉.基于VaR模型的我國商業銀行利率風險度量[J].金融經濟，2016（8）.

[3]王晉忠，高菲.運用衍生工具管理我國商業銀行利率風險的效率研究[J].武漢大學學報（哲學社會科學版），2015（6）：65、75.

[4]王清，邱靜，劉雨露.利率市場化下我國商業銀行利率風險管理研究——以工商銀行為例[J].西南金融，2015（10）：27、31.

[5]王勇飛.基于VaR模型的我國商業銀行利率風險度量研究——以銀行間市場債券質押式回購利率為例[D].重慶：西南政法大學，2012：28-35.

[6]史京鑫.互聯網金融風險防范的研究[J].對外經貿，2018（10）：102-104.

[7]謝曉雪.利率市場化與利率風險管理[J].中國金融，2012（15）：28-29.

[8]徐靈.基于VaR模型的我國商業銀行利率風險度量及實證研究[D].長春：吉林大學，2013：18-28.

[9]姚遠.商業銀行利率風險及其防范——基于2006～2010年7家上市銀行數據的驗證，金融論壇，2011（11）：45、51.

[10]趙敬.VaR模型在我國商業銀行利率風險度量中的應用研究[D].蘭州：蘭州商學院，2012：40-42.

[11]朱霞，劉松林.利率市場化背景下商業銀行利率風險管理[J].金融理論與實踐，2010（2）：40、43.

（責任編輯：張彤彤 藍 亮）

[作者簡介]羅熙茗（1998-），男，漢族，北京人，本科生在讀，研究方向：經濟學;付湘山（1998-），男，漢族，北京人，本科生在讀，研究方向：經濟學。

[基金項目]本文受到中國地質大學（北京）2019年“大學生創新創業訓練計劃”資助（項目編號：X201911415211）。