烏拉拉大戰“幻方”

張璋

狂風，吹亂了每一根頭發。

巨浪，拍打著每一塊礁石。

一艘閃耀著耀眼白光的太空飛船穿梭云間，疾沖而下……扎進了太平洋。浪花翻卷過后，飛船浮上海面，從打開的船艙門走出了我們的老朋友——烏拉拉和他手上拿著的一張紙。

話說，來過地球兩次的烏拉拉，對地球知識產生了無限興趣。在上一次返回太空的時候，順手拿走了一張紙：

將1～9這九個數，填入下面的方格中，使每行、每列、兩條對角線上的三個數字的和都相等。

求知欲極強的烏拉拉在抓禿了頭后，終于得出了答案：

可就在烏拉拉得意的時候，他發現紙的背面竟然還有一道題。震驚中，烏拉拉錯按了飛船操作鍵，致使飛船墜落太平洋。

河圖與洛書

趁著烏拉拉沒緩過勁兒，咱們先來聊聊“幻方”。要說幻方，就不得不講一個故事：

遠古時期，伏羲（xī）取得天下，把國家治理得井井有條，感動了上天，于是黃河中躍出一匹龍馬，背上馱著一張圖，作為禮物獻給他，這就是“河圖”，也是最早的幻方。伏羲憑借著“河圖”演繹出了八卦。后來大禹治洪水時，洛水中浮出一只大烏龜，它的背上有圖有字，被稱為“洛書”。

仔細觀察，“洛書”中共有黑、白圓圈45個。把這些連在一起的小圓和數目表示出來，就能得到由九個數組成的圖形：

你發現了嗎？

在上面3×3的九格圖中，每行、每列、對角線上的三個數的和都相等，我們把這種將數字安排在正方形格子中，使每行、列和對角線上的數字和都相等的方法，叫作“幻方”。而這樣3×3的數陣陣列就叫作“三階幻方”。

視線轉回，此時渾身濕透的烏拉拉，緊緊握著手里面的紙，返回駕駛艙，重新定位后……開始解題：

在下圖中的ABCD處填上適當的數，使下圖成為一個三階幻方。

謝天謝地，經過一番極致的腦力活動后，烏拉拉總算將題目解了出來。

根據幻方中“每行、每列、對角線上的三個數的和都相等”，可得：

①A+12+D=D+20+11，解A=19。所以每行、每列、對角線上的三個數的和為A+15+11=19+15+11=45。

②B=45-（16+19）=10;

③D=45-（20+11）=14;

④C=45-（16+11）=18。

烏拉拉看著紙上正面和背面的九格圖陷入了思考。

魔 數

烏拉拉總愛發呆，趁他發呆，咱們認識一下“魔數”。我們把每行、每列、對角線上的三個數相加總能得到的同樣的數，叫作“魔數”。比如“洛書”的魔數是15。幻方當然不僅僅只有三階幻方這一種，來看下圖。

這是一個四階幻方，魔數是8+11+14+1=34。仔細觀察，你發現了什么？按照要求計算一下：

□把任意一條直線上的四個數字加起來;

□把四個角上的數字加起來;

□把這個四階幻方看成一個大正方形，從大正方形里任意截出一個帶有四個數字的小正方形，把小正方形里的數字加起來;

□去掉中間的四個數和角上的四個數。把兩條側邊上剩下的數加起來。

如果你跟著計算，且結果無誤的話，你得到的結果都是相等的。那這些數字是怎樣巧妙地被排列在一起的呢？

抓破頭也想不通的你，還是看烏拉拉如何說吧。

思考過后的烏拉拉圈出了幾個數字：

烏拉拉發現，他可以通過這個“四階幻方”推出任意一個有不同魔數的“四階幻方”，而被圈出來的這四個數就是關鍵。

試試看：如果你希望的魔數是63，因為63比34大29，你只需把圈出來的數字加上29，即可。

怎么樣，是不是百試不爽？

“啪！”烏拉拉將紙扔進了垃圾桶，重新開啟飛船，沖出了大氣層。

幻方也奇葩

雖然烏拉拉又一次飛走了，但你要相信他還會回來的。在烏拉拉沒回來之前，咱們接著來看“幻方”。除了三階幻方、四階幻方外，當然還有五階幻方以及更大的幻方。

這是一個正常的五階幻方。幻方中包括1～25的所有數，魔數是65。如果你對更大的幻方感興趣的話，可以查一下六階幻方、七階幻方哦。接下來，一起來看“奇葩幻方”。

這是一個三角幻方，仔細觀察你會發現：從內到外每個頂點的三個數相加的和相等，除此以外，你還有其他發現嗎？

這是六角幻方，把處在每條直線上的六邊形里的數字相加，和都是相等的。除此以外，你還有其他發現嗎？

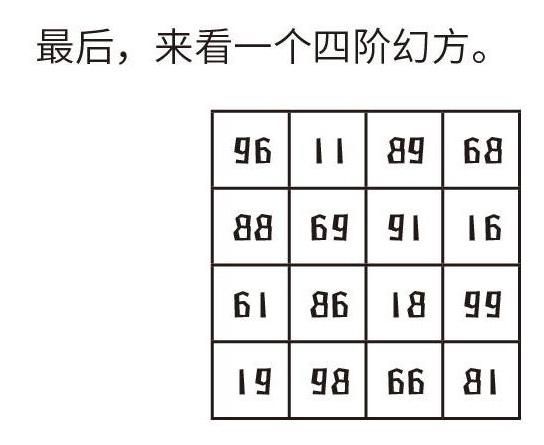
最后，來看一個四階幻方。

幻方中，各條線上四個數的組合，和都是264。現在，把書倒過來，你發現了什么？

怎么樣？是不是又一次刷新了“數學觀”！數學就是這樣，只要你仔細觀察，總能找到規律，發現樂趣。別忘了掃描“科普童話雜志社”微信二維碼，更多有趣的知識等著你哦！