非高斯噪聲下的回聲消除算法研究*
楊瑞麗,潘 琛
(商丘工學(xué)院信息與電子工程學(xué)院,河南 商丘476000)
1 引 言
通話質(zhì)量問(wèn)題是在人們的通信的過(guò)程中廣受關(guān)注的幾個(gè)具有決定性的核心問(wèn)題之一,其中通話的噪聲和回聲一直都是人們認(rèn)為影響電話通信質(zhì)量的主要決定性因素[1-2]。針對(duì)此類(lèi)問(wèn)題,已出現(xiàn)了比較成熟的回聲消除技術(shù), 基于自適應(yīng)濾波的回聲消除器就是被廣為認(rèn)可和應(yīng)用的一種回聲消除典型技術(shù),該類(lèi)技術(shù)通過(guò)有限長(zhǎng)脈沖響應(yīng)濾波器(FIR)進(jìn)行建模[3],得以實(shí)現(xiàn)的前提是假設(shè)回聲路徑符合線性特征。基于自適應(yīng)濾波的回聲消除技術(shù)常用的算法有最小均方誤差(Least Mean Square, LMS)算法和歸一化最小均方誤差(Normalized Least Mean Square, NLMS)算法等。
目前,雖然針對(duì)回聲消除的自適應(yīng)濾波算法研究已經(jīng)比較常見(jiàn),但大部分研究是基于高斯噪聲背景進(jìn)行的。在日常生活的現(xiàn)實(shí)和虛擬世界中, 由于雷電、颶風(fēng)、天電干擾、太陽(yáng)磁暴和宇宙電磁波脈沖等自然因素,報(bào)警器、電動(dòng)機(jī)、柴油機(jī)、發(fā)動(dòng)機(jī)、發(fā)電機(jī)等人為因素的相互影響,在對(duì)語(yǔ)音信號(hào)的處理、實(shí)時(shí)道路交通的檢測(cè)等復(fù)雜應(yīng)用場(chǎng)合中,普遍存在的不是只有符合高斯分布的噪聲,另一種非高斯所產(chǎn)生的噪聲同樣也廣泛地存在著[4]。非高斯噪聲往往都會(huì)在環(huán)境中呈現(xiàn)出很強(qiáng)的電磁波脈沖分布特性,與高斯分布的噪聲相比, 往往表現(xiàn)為分布更為厚重的噪聲拖尾現(xiàn)象。高斯噪聲和非高斯的噪聲都有可能被用來(lái)作為回聲消除系統(tǒng)的主要背景噪聲。
正是由于復(fù)雜環(huán)境所產(chǎn)生的非高斯噪聲往往具有特殊的特性,比如強(qiáng)烈的沖激性,嚴(yán)重地影響基于 范數(shù)優(yōu)化準(zhǔn)則的各種自適應(yīng)噪聲濾波系統(tǒng)和算法的性能。除此之外,通信系統(tǒng)中的回聲路徑通常都具有明顯的稀疏特性[5-6],在核心矩陣算法的理論基礎(chǔ)上與回聲消除系統(tǒng)的稀疏特性相互結(jié)合,可以有效地大幅度降低算法的計(jì)算量和成本,根據(jù)此特點(diǎn),文獻(xiàn)[7]利用比例矩陣思想,設(shè)計(jì)了修正的改進(jìn)比例歸一化最小均方誤差(Modified Improved Proportionate Normalized Least Mean Square,MIPNLMS)算法。根據(jù)符號(hào)算法(Sign Algorithm, SA)對(duì)非高斯噪聲具有良好適應(yīng)能力這一特點(diǎn)。在此將改進(jìn)比例矩陣算法的思想融合應(yīng)用到符號(hào)算法中,提出一種不僅適用于高斯噪聲,更能消除非高斯噪聲的改進(jìn)MIPNSA 算法,并將該歸一化算法應(yīng)用于修正噪聲的回聲消除的系統(tǒng)中,從而使回聲消除系統(tǒng)能夠較好地消除不同背景下的回聲。
2 非高斯噪聲條件下的新算法
高斯的和非高斯的噪聲都有可能被用來(lái)作為回聲消除系統(tǒng)的主要背景噪聲。非高斯噪聲所表現(xiàn)的脈沖特性,嚴(yán)重影響了基于L2范數(shù)優(yōu)化計(jì)算準(zhǔn)則的自適應(yīng)濾波算法的回聲消除性能,現(xiàn)已有研究工作明確論證了符號(hào)矩陣的算法能夠有效抑制非高斯的噪聲[8]。同時(shí),回聲路徑矩陣也具有明顯的稀疏特性,該特性同樣影響自適應(yīng)濾波算法對(duì)回聲消除的性能。綜上分析,考慮高斯與非高斯兩種噪聲作為回聲消除的背景噪聲,可將比例式濾波矩陣的設(shè)計(jì)思想與NSA 算法相結(jié)合,設(shè)計(jì)出適用于非高斯噪聲背景下實(shí)現(xiàn)回聲消除的改進(jìn)MIPNSA 算法,其中采用α 穩(wěn)定分布表述非高斯分布的方法描述非高斯噪聲。
在非高斯噪聲背景下,NSA 算法[9]因具有良好性能而被廣泛應(yīng)用,該算法是通過(guò)將NLMS 算法和SA 算法相結(jié)合而得到的,不僅保留了NLMS 算法所具有的收斂速度快的特點(diǎn),同時(shí)又對(duì)非高斯噪聲具有良好的抑制能力,設(shè)濾波器系數(shù)向量為h?(n),系統(tǒng)的輸入向量為x(n),誤差信號(hào)為e(n),固定步長(zhǎng)參數(shù)為μ,則NSA 算法的主要的迭代函數(shù)方程可以表示為下式:
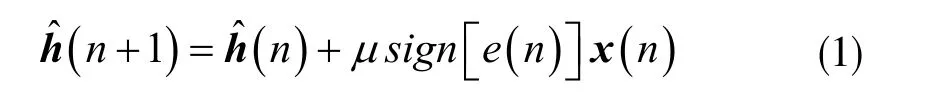
已發(fā)表的回聲消除相關(guān)研究工作表明,自適應(yīng)濾波器的階數(shù)、收斂步長(zhǎng)、系統(tǒng)稀疏度等都是影響自適應(yīng)濾波算法性能的主要因素[10]。關(guān)于系統(tǒng)稀疏度與算法性能之間的算法研究亦較為成熟,已知現(xiàn)有的IPNLMS 算法對(duì)系統(tǒng)的稀疏特性則具有良好的適應(yīng)能力,該算法是在PNLMS 算法的基礎(chǔ)上針對(duì)系統(tǒng)稀疏度進(jìn)行改進(jìn)而提出的。設(shè)有對(duì)角矩陣G(n),指正參數(shù)ζ 和φ,則IPNLMS 主要的迭代函數(shù)方程為:

把式(2)中系數(shù)比例矩陣帶入如(1)式所示的SA算法迭代公式中,整理為迭代方程可表示為如下式的IPNSA 算法:
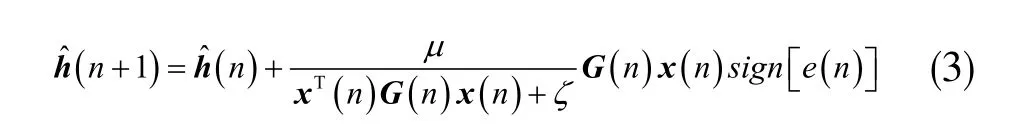
根據(jù)式(2),系統(tǒng)比例項(xiàng)權(quán)重會(huì)直接影響IPNLMS算法的收斂速度。文獻(xiàn)[7]的MIPNLMS 算法給出了系統(tǒng)比例項(xiàng)的權(quán)值與整個(gè)系統(tǒng)稀疏度的關(guān)系表述,但MIPNLMS 算法并沒(méi)有明確系統(tǒng)比例項(xiàng)的權(quán)值取最優(yōu)時(shí)系統(tǒng)稀疏度的取值。

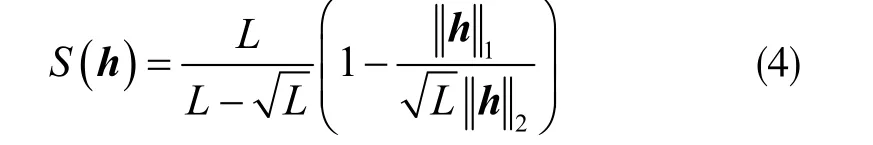
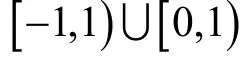
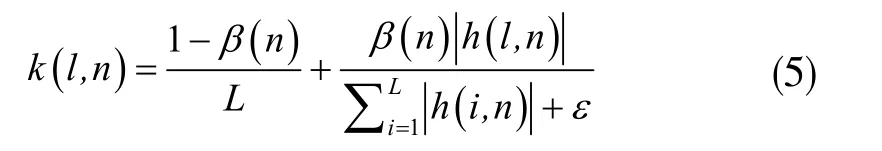
令γ 和δ 分別表示正參數(shù),則β(n)可表示為:
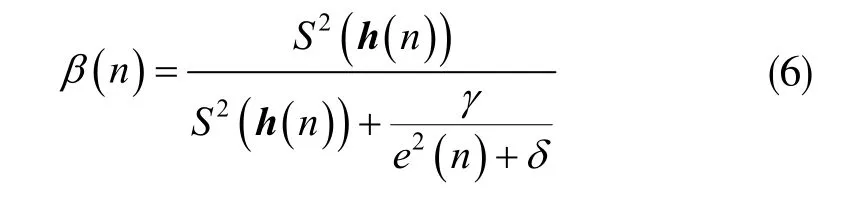
設(shè)MIPNLMS 算法中的對(duì)角矩陣為K(n),根據(jù)(4)、式(5)、式(6),K(n)可表示為:
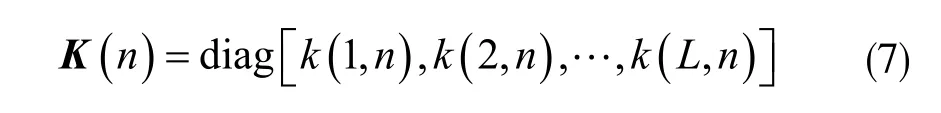
已知式(7),則MIPNLMS 算法迭代更新函數(shù)可表示為:
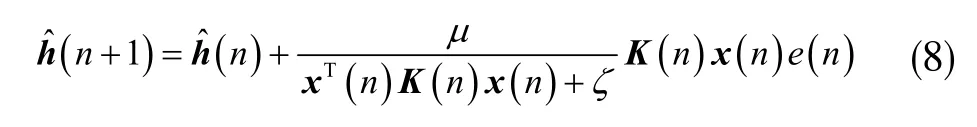
根據(jù)式(8),結(jié)合式(1),可將改進(jìn)的MIPNSA 算法的迭代更新函數(shù)表示為:
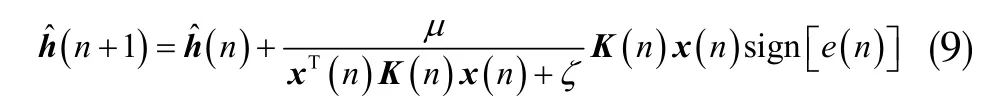
根據(jù)迭代更新函數(shù)式(9),所提的改進(jìn)MIPNSA算法在輸入非高斯噪聲后可以表示為如下各式所示的自適應(yīng)過(guò)程:
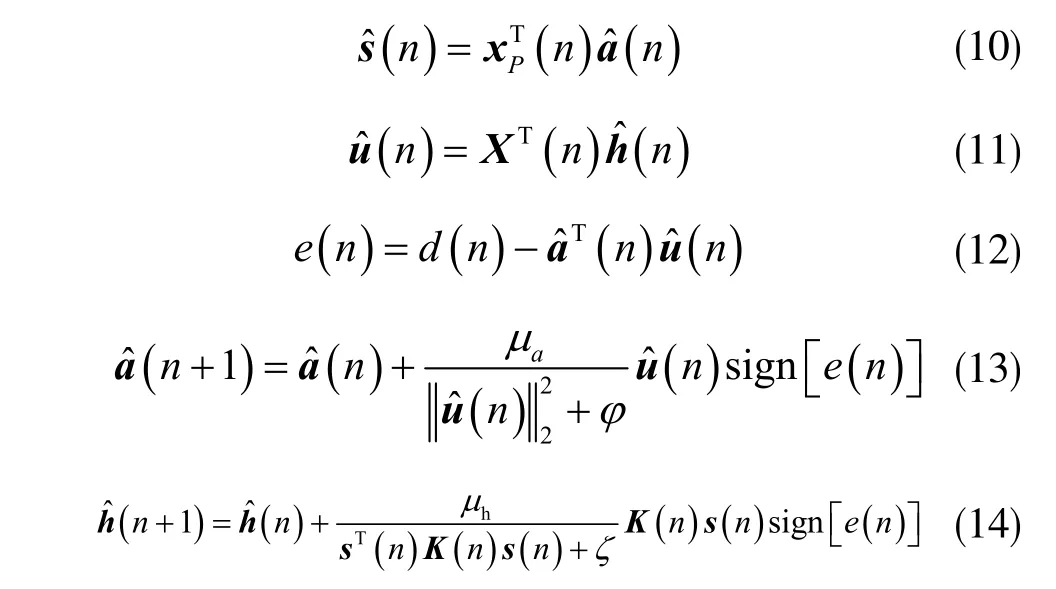
3 仿真實(shí)驗(yàn)
3.1 仿真條件
仿真實(shí)驗(yàn)所采用的輸入信號(hào)包括兩種形式,即隨機(jī)信號(hào)和相應(yīng)的語(yǔ)音信號(hào)。將兩種輸入信號(hào)分別進(jìn)行相應(yīng)的MATLAB 仿真。在仿真實(shí)驗(yàn)中,F(xiàn)IR 濾波器的長(zhǎng)度等于128,并使線性的聲學(xué)回聲路徑的長(zhǎng)度為128。
設(shè)脈沖響應(yīng)的長(zhǎng)度為L(zhǎng),以r(n)表示范圍為[-0.2,0.2]的隨機(jī)數(shù),δ 為Dirac 函數(shù),初始狀態(tài)令L=128,初始化h?(n)為零向量,根據(jù)下式即可計(jì)算線性聲學(xué)回聲路徑:
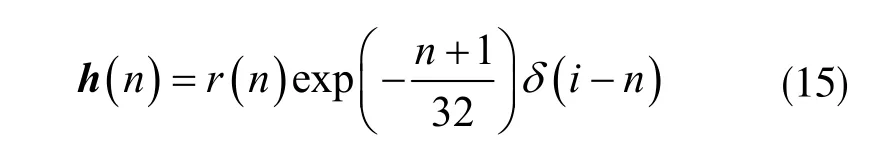
其中,n,i=0,1,...,L-1。
回聲路徑的特性如圖1 所示,具有明顯的稀疏特點(diǎn),其中系數(shù)較大的數(shù)值只占少數(shù),系數(shù)較小的數(shù)值占大部分,并且大部分接近零。
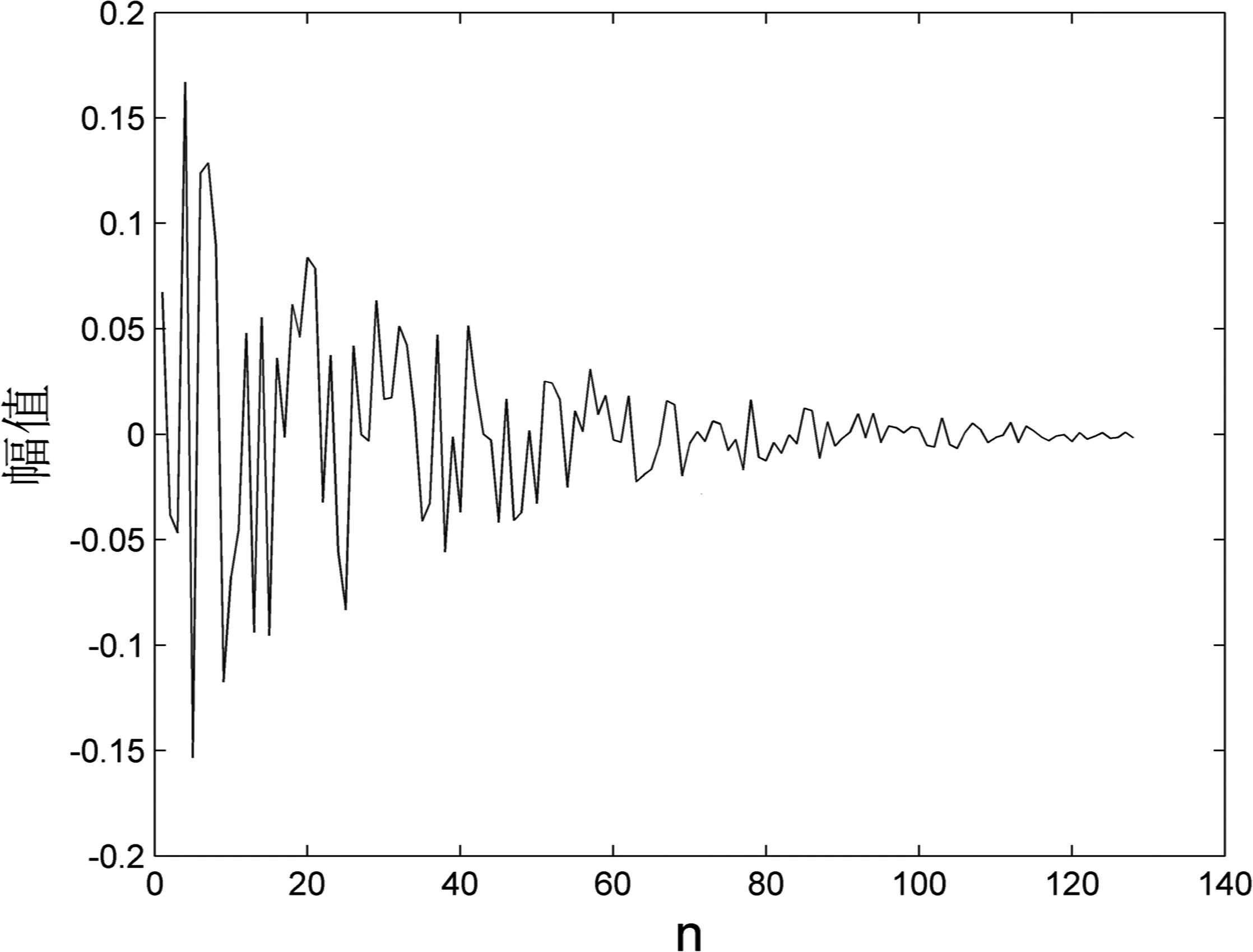
圖1 聲學(xué)回聲路徑脈沖響應(yīng)h
3.2 性能指標(biāo)和參數(shù)設(shè)置
實(shí)驗(yàn)進(jìn)行的條件是各對(duì)比算法取等效步長(zhǎng),各種算法實(shí)驗(yàn)結(jié)果的綜合性能表現(xiàn)好壞利用權(quán)誤差向量范數(shù)(WEVN)的收斂曲線函數(shù)來(lái)準(zhǔn)確衡量和分析評(píng)價(jià), 從而充分說(shuō)明各種算法綜合實(shí)驗(yàn)性能的總體優(yōu)劣。
線性系數(shù)的WEVN 表達(dá)式為:
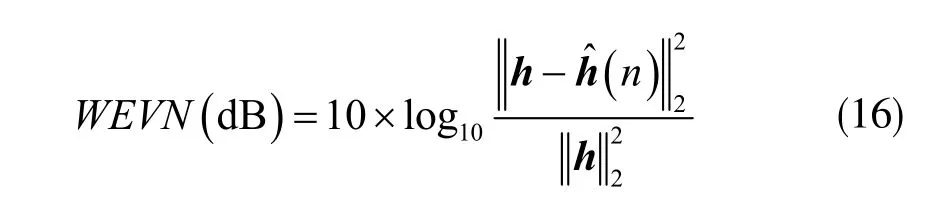
隨著WEVN 的取值的變小,即表示系統(tǒng)中的自適應(yīng)濾波器和所需要跟蹤的未知濾波器系統(tǒng)越來(lái)越逼近。
設(shè)分散系數(shù)為γ,令高斯環(huán)境下的信噪比為SNR1,非高斯環(huán)境下的信噪比為SNR2,分別表示為如下二式:
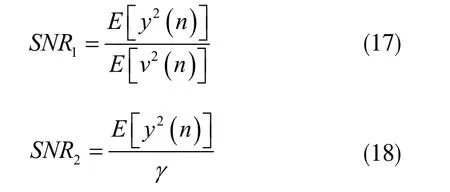
仿真實(shí)驗(yàn)將高斯條件和非高斯濾波噪聲兩種條件下的濾波信噪比分別精確設(shè)置為20dB,其中輸入的非高斯噪聲取α=1.5 時(shí)具有穩(wěn)定分布。
3.3 仿真結(jié)果分析
在進(jìn)行仿真實(shí)驗(yàn)時(shí),每個(gè)實(shí)驗(yàn)仿真結(jié)果統(tǒng)一采用30 次獨(dú)立仿真實(shí)驗(yàn)的平均結(jié)果,符合實(shí)驗(yàn)的公平原則。
3.3.1 隨機(jī)信號(hào)仿真實(shí)驗(yàn)
仿真實(shí)驗(yàn)中輸入信號(hào)為高斯白噪聲,均值為零。當(dāng)輸入高斯噪聲時(shí),各算法性能比較如圖2 所示;當(dāng)輸入非高斯噪聲時(shí),各算法性能比較如圖3 所示。
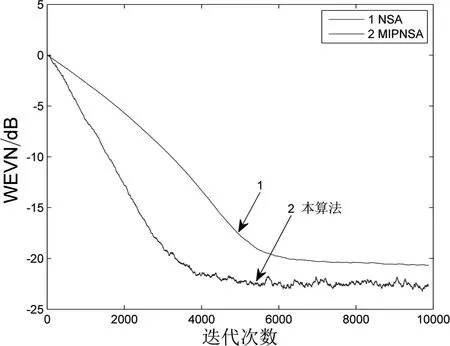
圖2 高斯噪聲下濾波器系數(shù)收斂曲線(隨機(jī)信號(hào))
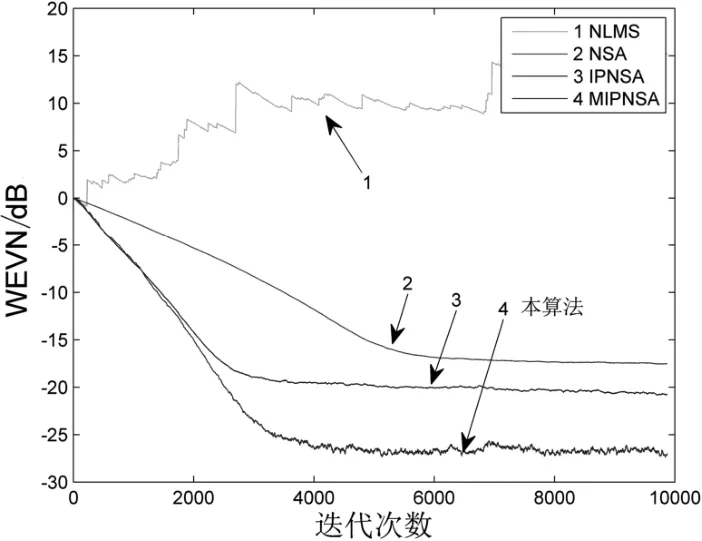
圖3 非高斯噪聲下濾波器系數(shù)收斂曲線(隨機(jī)信號(hào))
對(duì)比圖2 和圖3 中的仿真結(jié)果,可以明顯看出:在非高斯噪聲的條件下,傳統(tǒng)算法的回聲消除已經(jīng)開(kāi)始出現(xiàn)失效。此外,與其他各類(lèi)傳統(tǒng)高斯噪聲算法相比,此處提出的改進(jìn)MIPNSA 算法不管是在高斯噪聲環(huán)境下還是非高斯噪聲的環(huán)境下,回聲消除效果均表現(xiàn)較好。
3.3.2 語(yǔ)音信號(hào)仿真實(shí)驗(yàn)
仿真實(shí)驗(yàn)中采集非平穩(wěn)的真實(shí)語(yǔ)音信號(hào)作為系統(tǒng)的輸入信號(hào),輸入的語(yǔ)音信號(hào)如圖4 所示,該信號(hào)是樣本長(zhǎng)度為20000 和頻率長(zhǎng)度為4kHz 的采樣噪聲,其他參數(shù)的取值與均值為零的高斯白噪聲相同。
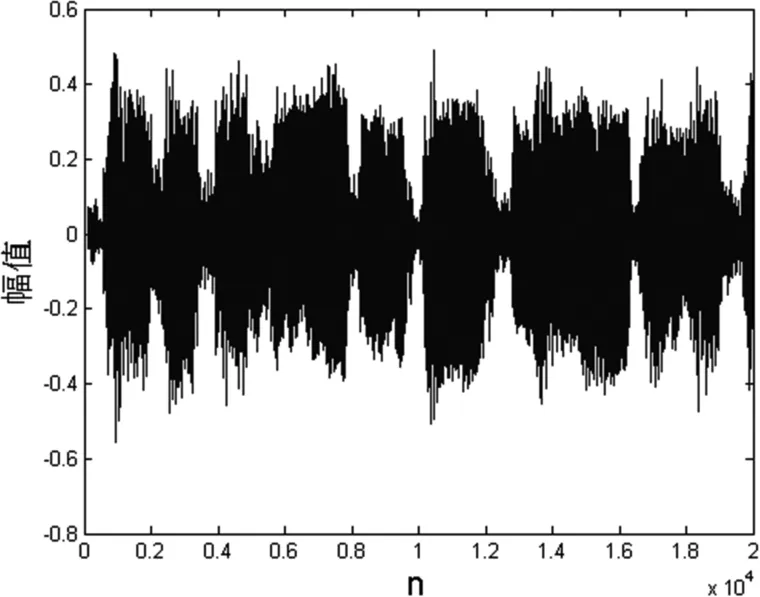
圖4 語(yǔ)音信號(hào)
兩種噪聲條件下的濾波器系數(shù)收斂曲線如圖5和圖6 所示。
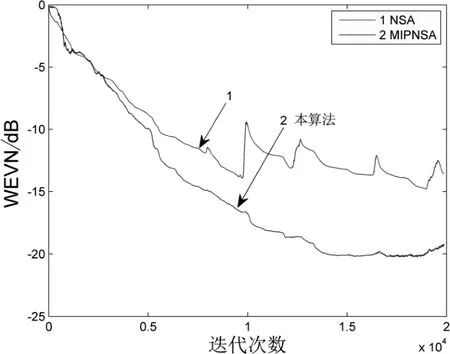
圖5 高斯噪聲下濾波器系數(shù)收斂曲線(語(yǔ)音信號(hào))
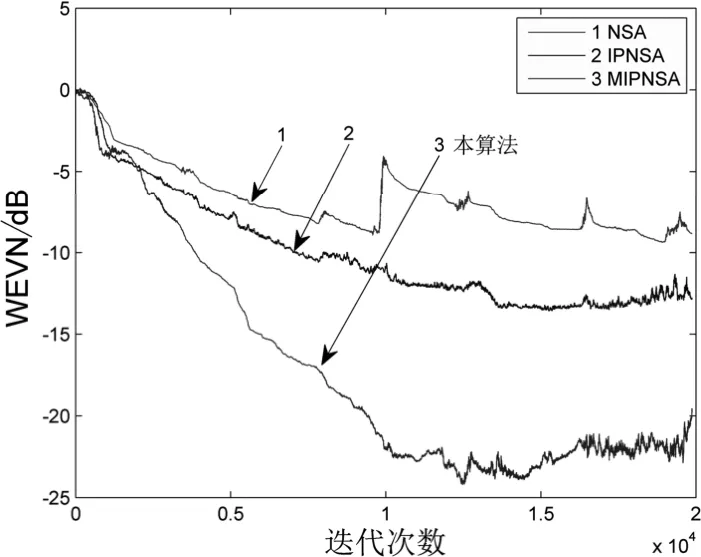
圖6 非高斯噪聲下濾波器系數(shù)收斂曲線(語(yǔ)音信號(hào))
對(duì)比如圖5 和圖6 中的仿真結(jié)果,可明顯看出:當(dāng)語(yǔ)音信號(hào)作為濾波器的輸入信號(hào)時(shí),在高斯噪聲和非高斯噪聲兩種環(huán)境下,根據(jù)不同濾波器算法的非平穩(wěn)收斂曲線,仍然能夠反映本改MIPNSA 算法對(duì)高斯噪聲和非高斯噪聲的消除效果。雖然語(yǔ)音信號(hào)作為輸入時(shí)的非平穩(wěn)的特性直接導(dǎo)致本算法的收斂曲線性能比預(yù)期有所降低,但相比于實(shí)驗(yàn)中其他算法的仿真結(jié)果,本算法對(duì)非高斯噪聲的效果仍然表現(xiàn)較好。
4 結(jié) 束 語(yǔ)
隨著通信技術(shù)和多媒體處理技術(shù)的不斷發(fā)展,社會(huì)對(duì)便利性、互動(dòng)性日益增長(zhǎng),一般的通信質(zhì)量已經(jīng)難以滿足人們的日常需求。在通信質(zhì)量的各種指標(biāo)中,語(yǔ)音清晰度是最基本也是最主要的一點(diǎn)。為保證語(yǔ)音清晰度,最關(guān)鍵是要更好地去除回聲和噪聲的影響。通過(guò)實(shí)驗(yàn),分別采用隨機(jī)信號(hào)和語(yǔ)音信號(hào)作為回聲消除系統(tǒng)的輸入,對(duì)高斯噪聲和非高斯噪聲實(shí)驗(yàn)仿真的結(jié)果進(jìn)行分析,可以得出以下結(jié)論:一、所提的MIPNSA 算法能夠適用于不同類(lèi)型和背景的噪聲,對(duì)高斯噪聲和非高斯噪聲均能夠表現(xiàn)出較好的抑制噪聲能力;二、明確系統(tǒng)的稀疏性與比例項(xiàng)的權(quán)值兩者之間的關(guān)系,便可更好地實(shí)現(xiàn)自主控制系統(tǒng)比例項(xiàng)的權(quán)重,并對(duì)其進(jìn)行適當(dāng)?shù)倪x值,使得算法能夠進(jìn)一步改善回聲消除的效果。相較于仿真實(shí)驗(yàn)中采用的傳統(tǒng)自適應(yīng)濾波算法,所提的新算法具有更快的收斂速度以及更佳的系統(tǒng)穩(wěn)態(tài)性能。

