低軌衛星星座動態波束關閉算法

劉帥軍，胡月梅，范春石，凌騰，劉立祥

（1.中國科學院軟件研究所，北京 100190；2.北京中科宇航探索技術有限公司，北京 101100；3.航天東方紅衛星有限公司，北京 100094）

1 引言

低軌（LEO,low earth orbit）衛星星座以星地鏈路時延低、傳播損耗小等優點，在服務全球多媒體及物聯網等業務上發揮著重要的作用。考慮到衛星鏈路可用帶寬較小，星載發射機通常采用多波束天線配置以提供空分增益，提升系統傳輸效率。同時，為實現全球范圍的連續無縫覆蓋，需要LEO 星座的各波束間可以無縫地覆蓋全球。然而，這種全球覆蓋需求造成了LEO 波束間存在較大的重疊覆蓋，且帶來了大量無用波束的資源開銷，該問題在近極軌道星座下的高緯度區域覆蓋中尤其突出[1-2]。例如，近極軌道LEO 星座——銥星（Iridium）系統，為避免相鄰衛星多波束間在高緯度區域產生嚴重重疊，該系統采用動態波束關閉策略，降低系統運行過程中的相互干擾，并節省星上功率等資源開銷。相關文獻指出，銥星系統在實際運行過程中僅需2 150 個波束（關閉1 018 個波束）即可滿足覆蓋全球的通信業務[3]。

低軌星座網絡動態波束關閉策略是在多波束低軌衛星星座場景下確定衛星多個波束如何關閉的策略，需在既定目標和約束下從給定波束集合中選擇一組波束進行關閉。針對該問題，國內外航天機構開展了相關研究。文獻[4]提出了一種全球低軌星座系統中的動態波束關閉方法，主要考慮了在星載太陽能帆板充放電約束下的波束開關策略，通過地基控制中心集中調度以最大化衛星功率利用率。文獻[5]提出了一種干擾抑制技術，綜合考慮了低軌星座內波束重疊、負載輕重等因素，通過確定第一衛星第一波束覆蓋帶而關閉剩余波束，同時由第二衛星第二波束子集進行補充覆蓋，在滿足全球連續覆蓋下可降低星座內的干擾并優化負載均衡。與文獻[5]類似，文獻[6-7]提出了通過動態波束關閉實現低軌星座頻率規避的方法，重點考慮了與地球同步軌道（GSO,geosynchronous orbit）衛星的干擾規避問題。

現有研究以頂層策略為主，即僅定義或約束一些波束關閉的原則，尚未進行嚴謹的數學模型建立及動態波束關閉算法的深入研究。在此基礎上，本文建立低軌星座網絡動態波束關閉的系統場景及數學模型，并在給定目標函數和約束條件下建立、求解優化問題。本文首先對低軌星座網絡動態波束關閉的系統場景和數學模型進行建模，在保證全球連續無縫覆蓋和有業務傳輸的波束不關閉這2 項約束條件下，建立了旨在最小化低軌星座激活波束個數的最優化問題，從而最小化由波束間重疊所造成的干擾與資源閑置。然后，通過將待求解的最優化問題轉化為集合覆蓋問題（SCP,set cover problem），闡明了該問題的NP 完全屬性；結合低軌星座網絡動態運行特點，急切需要一種快速收斂且高效的探索式算法。基于此，本文提出一種門限控制截斷的探索式算法，其基本思想是在給定時間域內進行探索，以保證高動態低軌星座網絡下的快速收斂特性。最后，仿真結果以實際低軌星座網絡——銥星系統為仿真場景，驗證了所提算法在降低波束重疊方面的效果。

本文主要工作歸納如下。

1)建立了低軌星座網絡動態波束關閉的數學模型。基于低軌星座衛星動力學方程、星上波束配置、星座覆蓋要求等約束，以最小化星座激活波束個數為目標，建立了低軌星座網絡動態波束關閉的最優化模型。

2)提出一種基于門限控制截斷的探索式算法。對動態波束關閉優化問題進行轉化與分析，證明了該問題是NP 完全問題；結合低軌星座對地覆蓋的高動態特性，提出了具有時效性的基于門限控制截斷探索式算法。

2 系統模型與問題建模

2.1 LEO 衛星星座場景描述

本文以低軌多波束衛星星座為研究對象，該星座網絡內各星采用星載多波束天線。記該低軌星座的衛星個數為NS，星座內衛星為si,i=1,2,…,NS。對于每顆衛星而言，采用半長軸、偏心率、軌道傾角、升交點赤經、近地點幅角和近地點時刻這6 個參數即可實現衛星位置與運行規律的表征。為了更清晰地表征星座網絡的空間關系，定義衛星本體坐標系[8-9]：以衛星平臺質心為坐標原點O，以原點指向地心為正Z軸，以原點指向衛星切線運行方向為正X軸，根據右手法則得到Y軸。衛星本體坐標系如圖1 所示。

圖1 衛星本體坐標系

記每顆衛星的波束個數為NB，bi,j表示衛星si的第j個波束，i=1,2,…,NS,j=1,2,…,NB，則系統總波束個數為NB,tot=NSNB。記星座網絡的目標覆蓋區域為G，對于任意終端gk={Latgk,Longk}而言，若該終端位于服務區域內，則表示為gk∈G；否則表示為gk?G。

衛星多波束通過星載多波束天線生成，即多波束空間指向與衛星平臺自身密切相關，基于此，衛星多波束空間指向的定義需以衛星本體坐標系為參考。對于波束bi,j而言，其在衛星si本體坐標系下，定義其空間指向，其中，Azi,j為方位角，Eli,j為仰角。方位角定義為以正X軸順時針方向到波束指向在XOY平面投影的角度，仰角定義為波束指向與XOZ平面的夾角。同樣，可求得在衛星si本體坐標系下衛星si指向終端gk的方向為。進一步，通過式(1)可獲得空間向量對應的OXYZ表示，即。

此時，波束指向與衛星終端指向的空間夾角θi,j,k如式(2)所示。

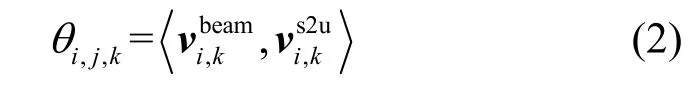
其中，θi,j,k可根據空間角度關系計算得到。衛星多波束指向示意如圖2 所示。

圖2 衛星多波束指向示意

衛星各波束采用圓波束模型，對應的波束角（BW,beam width）記為。對于采用具有其他非圓波束的星座網絡而言，也可通過求解終端與星間相對空間角度判斷覆蓋與否。對于波束bi,j、終端gk而言，當衛星終端指向與波束指向之間空間夾角小于該波束半波寬時，認為終端被該波束覆蓋，否則認為該終端不在波束覆蓋范圍內。為此，定義終端-波束相關的覆蓋因子ci,j,k，表征終端gk是否被波束bi,j覆蓋。覆蓋因子ci,j,k的計算式為

同時，定義波束激活與否因子ai,j，以表征波束處于激活或關閉的狀態。ai,j計算式為

2.2 問題建模

本文研究目標是最小化星座網絡工作的波束數，如式(5)所示。

當星座網絡內部分波束關閉時，應滿足如下2個約束條件。

約束1保證服務區域的覆蓋，即在若干波束關閉的情況下，對于服務區域內任意終端而言，至少存在一個激活的波束可覆蓋該終端。該約束為

約束2若有正在進行業務傳輸的波束不可關閉，不妨將此波束集合記為 Bserving，Bserving?B。該約束為

綜上，本文研究的動態波束關閉最優化問題為

3 門限控制截斷的動態波束關閉算法

本節描述了所提門限控制截斷的動態波束關閉算法。首先對式(8)中的優化問題進行分析和轉化，進而設計所提算法。

3.1 問題分析與轉化

考慮到式(8)所建立的最優化問題屬于二重求和問題，目標是最小化激活波束的個數，而約束需保證連續覆蓋與有業務傳輸波束不關閉。由此，可將此二重求和重寫為以波束為基的一重求和問題。

構造波束與終端相關的一個矩陣D，該矩陣的行表示一個波束，列表示終端，如式(9)所示。

記dn為矩陣D的行向量，任意若干組行向量組成子矩陣，則最優化問題(8)可轉化為求解一個最小SCP，如式(10)所示。

以下將闡明2 個引理，以證明本文所求解動態波束關閉問題（即式(8)）是一個NP 完全問題。

引理1式(8)的優化問題P 等價于式(10)的優化問題Q。

證明由式(9)可知，矩陣D是由覆蓋因子ci,j,k組成的二維矩陣，而最優化問題Q 目標是最小化子矩陣D'的行向量個數，即最小化波束個數；優化問題Q 的約束1 保證了子矩陣中至少存在一個行向量（即波束），可滿足對覆蓋區域G 內任意終端的覆蓋；進一步結合由式(9)對矩陣D的定義可知，優化問題Q 的約束2 保證了正在進行業務傳輸的波束處于激活狀態。綜上，優化問題Q 在目標函數與2 個約束條件上與優化問題P 是一致的，即式(8)的優化問題P 等價于式(10)的優化問題Q。

證畢。

引理2式(10)的優化問題Q 是一個最小SCP。

證明SCP=(X,Y,W)描述為給定一個全集X及該全集的若干子集Y，有∪?y∈Y=X，記子集Y內每個元素的權重為w(y)，則目標是找出一個集合F?Y，在滿足全集X所有元素下，∪?y∈F=X，使該集合權重和最小，即。結合優化問題Q，可將其建模為一個SCP 實例，具體如下。令X={k|k=1,2,…,K}，Y={yn|n=1,2,…,NB,tot}，且有yn={k|dn,k=1}，由星座內所有波束可對區域G 內終端全覆蓋可知，∪?y∈Y=X，且w(y)=1。綜上，優化問題Q 是一個最小SCP。

證畢。

結合上述2 個引理，可給出如下定理及證明。

定理1式(8)的優化問題P 是NP 完全問題。

證明由引理1 可知，式(8)優化問題P 等價于式(10)優化問題Q；由引理2 可知，式(10)優化問題Q 是一個最小SCP；同時，SCP 是已知的NP 完全問題[10-12]。綜上可知，本文待求解的動態波束關閉優化問題P 是NP 完全問題。

證畢。

3.2 門限控制截斷探索式算法

由3.1 節可知，本文待求解的問題是一個最小SCP。針對此問題的求解方法可分為精確求解方法和啟發式求解方法。考慮到SCP 的NP 完全屬性，使用精確求解方法雖然可以保證得到最優解，但隨著求解問題規模的不斷擴大，精確求解方法的求解時間呈指數上升，此時無法保證在可接受的時間內返回一個候選解。相比而言，啟發式方法在合理的求解時間內能夠獲得一個盡可能好的候選解，但是不能保證這個候選解是最優解。考慮到本文所求問題的規模較大，例如，對于銥星系統的3 168 個波束，終端全球分布取1 經度×1 緯度情況下，則需求解矩陣為3 168×64 800 的規模；對于OneWeb 系統，則需求解矩陣為11 520×64 800 的規模，精準求解方法求解時間開銷難以接受。

基于此，本文給出一種門限控制截斷的探索式算法，基本思想是在保證全覆蓋與某些波束不關閉的約束下，逐次嘗試關閉波束；為保證算法的時效性，采用了門限控制的方式以截斷執行時間窗。在每次執行過程中選擇哪個波束進行關閉則是本文算法的難點。首先，給出本文算法執行的總體流程設計；然后，詳述算法過程中關閉波束選擇的設計。

1)門限控制截斷探索式算法總體流程設計

門限控制截斷的探索式算法基本流程如下。

步驟1令波束-終端相關的覆蓋矩陣D'=D，且在D'中選擇一個行向量dn，將此行向量從矩陣D'中去除（即等價于關閉行向量dn所代表的波束）；令Niter=0。

步驟2若D'仍滿足式(10)中的約束條件，則更新D=D'，返回步驟1 繼續執行；否則，迭代搜索次數Niter加1，跳至步驟3。

步驟3判斷迭代搜索次數是否超過門限，即Niter＞NTh，若滿足，跳至步驟4；否則，返回步驟1。

步驟4算法結束，輸出波束關閉算法的解D。

2)關閉波束選擇的設計

關于步驟1 中“在D'中選擇一個行向量dn”，選擇dn的依據如下。

原則1有正在進行業務傳輸的波束不關閉。

原則2重疊覆蓋最嚴重的波束應優先選擇關閉。對該波束所覆蓋的終端而言，其波束平均覆蓋重數（同時被波束覆蓋的次數）最大的將被優先選擇以關閉。因此行向量dn的選擇方法如式(11)所示。

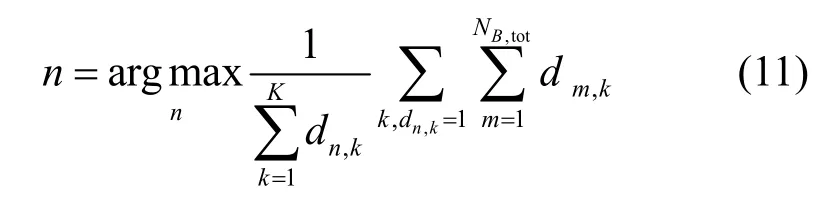
4 仿真結果與分析

4.1 仿真配置

以銥星星座網絡為仿真場景，銥星星座空間段為66 顆星，每顆星具備48 個點波束，則銥星星座網絡波束個數總計為66×48=3 168。銥星星座的仿真參數配置[13-14]如表1 所示。

表1 仿真參數配置

銥星采用星載三幅相控陣天線，每副天線生成16 個點波束。考慮到衛星實際48 波束的波束寬度及指向等并未公布，基于銥星星座終端最小工作仰角8.2°等參數，本文仿真場景采用表2 中的點波束配置。

表2 銥星單幅相控陣天線16 波束仿真配置

其余兩幅相控陣生成的32 副天線，只需在上述天線基準上分別順時針和逆時針旋轉120°即可。通過仿真可以得到48 波束配置下的單星覆蓋區域仰角及多波束分布特性，如圖3 所示。其中，緯度的正值表示北緯，負值表示南緯；經度的正值表示東經，負值表示西經。圖3(a)為終端對衛星的仰角分布。從圖3(a)可以看出，處于衛星星下點區域的終端仰角較大，星下點處終端對衛星的仰角為90°；隨著終端位置遠離星下點，仰角越來越小，衛星對單顆終端的覆蓋可實現最小工作仰角8.2°，與銥星網絡工作參數一致。圖3(b)為星載48 波束對地覆蓋，不同顏色表示48 個波束的對地覆蓋區域。由于本文假設同一波束寬度的圓波束配置，因此，星下點附近的波束覆蓋范圍較小，遠離星下點區域的波束覆蓋范圍較大。

4.2 結果與分析

通過仿真可知，銥星星座網絡可關閉1 255 個波束，僅1 913 個波束同時工作即可滿足全球覆蓋要求，即本文所提方案可節省39.61%的波束資源。銥星星座網絡波束全部激活情況下對地覆蓋分布如圖4 所示。采用本文波束關閉策略后，銥星星座網絡對地覆蓋分布如圖5 所示。

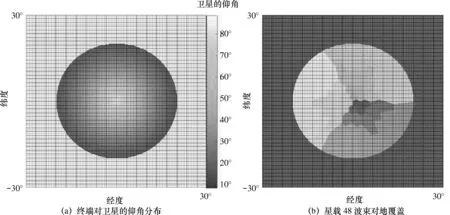
圖3 衛星覆蓋區域仰角及多波束分布

由圖4 可以看出，銥星星座對地覆蓋在赤道與中低緯度區域較稀疏，而在極地區域及高緯度區域較密集。對于任意終端而言，至少有一個波束的覆蓋保證了網絡的全球覆蓋，而極地區域存在多達15 個波束重疊覆蓋。相比而言，當采用波束關閉策略后，極地區域可在保證全球連續覆蓋的情況下，降低至最多7 個波束重疊覆蓋。圖4 和圖5 的覆蓋分布可進一步通過波束覆蓋重數的累計分布函數（CDF,cumulative distribution function）來表征，如圖6所示。

圖4 銥星星座網絡波束全部激活情況下對地覆蓋分布

圖5 銥星星座網絡采用波束關閉策略后對地覆蓋分布

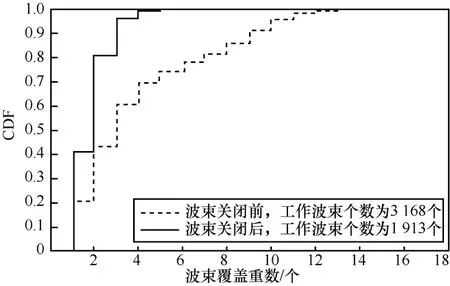
圖6 銥星星座網絡波束覆蓋重數CDF

由圖6 可知，波束關閉前，有超過80%的終端具備至少2 個波束重疊覆蓋；采取波束關閉策略后，該比率下降到60%。波束關閉前，39%的終端超過了3 個波束重疊覆蓋；采取波束關閉策略后，該比例下降到3%。由此可看出，波束間重疊覆蓋的問題得到顯著改善。進一步地，探究衛星工作波束個數與衛星工作緯度的關系，如圖7 所示。其中，緯度的正值表示北緯，負值表示南緯。

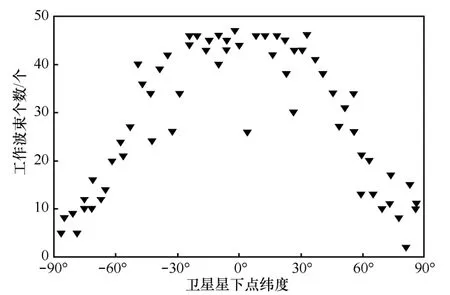
圖7 波束關閉策略后激活波束個數與星下點緯度的關系

由圖7 可知，對于運行在中低緯度上空的衛星而言，波束工作的個數較多，如緯度低于40°區域內，衛星工作波束個數在40 個以上，即僅關閉了不到8 個波束；對于運行在高緯度上空的衛星而言，波束工作的個數較少，如緯度高于75°區域內，衛星工作波束個數大多在10 個以下，即關閉了38 個波束。

綜上，針對星座網絡在高緯度區域重疊覆蓋嚴重的問題，本文采取的波束關閉策略可顯著降低高緯度區域重疊波束覆蓋，在保證全球覆蓋的基礎上最小化星座系統的工作波束個數，在降低波束間干擾的同時降低了39.61%的波束資源開銷。

5 結束語

針對低軌多波束衛星星座網絡存在的波束間嚴重的重疊覆蓋問題，本文建立了波束關閉優化問題，在闡明該問題的NP 完全特征后，采用探索式方法進行求解。以銥星星座網絡為仿真場景，對于系統內3 168 個波束僅需1 913 個波束同時工作即可滿足要求，降低了39.61%波束資源的開銷。下一步工作主要包括考慮非正圓波束形狀下的動態關閉方法，如高橢圓波束及其他成形波束；考慮在對GSO 衛星干擾規避下的動態波束關閉方法。