自動照準型全站儀配合跟蹤靶球測量可行性及精度驗證研究

孟凡明，王 偉，豐寅帥

(1.海軍裝備部駐沈陽地區軍事代表局，遼寧 沈陽 110031;2.海軍工程大學 艦船與海洋學院，湖北 武漢 430033)

隨著現代工業的發展，以捶球、卡尺為主的傳統測量工具已經逐漸被全站儀、跟蹤儀等高精度的測量工具所取代[1]。其中跟蹤儀可以實現目標的快速跟蹤和高精度定位[2]，但也存在著對測量環境要求較高、造價昂貴等缺點[3];全站儀具有成本較低、測量環境適應度高、操作簡單等優點[4]，在船舶修造領域的測量作業中應用較為廣泛，但由于測量現場工況復雜、被測物體尺寸較大，往往需要進行多站位、長距離測量[5]。全站儀常用的棱鏡、免棱鏡、反射片3種測量模式在此類工況下，精度會出現一定的下降，同時，全站儀需要人工對目標進行瞄準，也引入了不同程度的人為誤差。針對以上問題，本文提出了一種自動照準型全站儀配合跟蹤靶球進行測量的方法。

1 基本理論

1.1 坐標轉換原理

在船舶修造現場的測量作業中，由于各類障礙物的遮擋，在一個站位下往往無法通視全局[6]，目前常采用全站儀自由設站、多級轉站的方法進行測量。

如圖1所示，坐標系O0-X0Y0Z0表示自然坐標系的空間位置，坐標系O1-X1Y1Z1表示基準坐標系的空間位置，坐標系O2-X2Y2Z2表示在當前站位下全站儀的測量坐標系的空間位置，在轉站過程中，通過坐標轉換參數可以將點在不同站位坐標系下的坐標數據統一到一個坐標系中，坐標轉站參數可以通過同一組公共點在不同站位坐標系的坐標數據求取[7]。

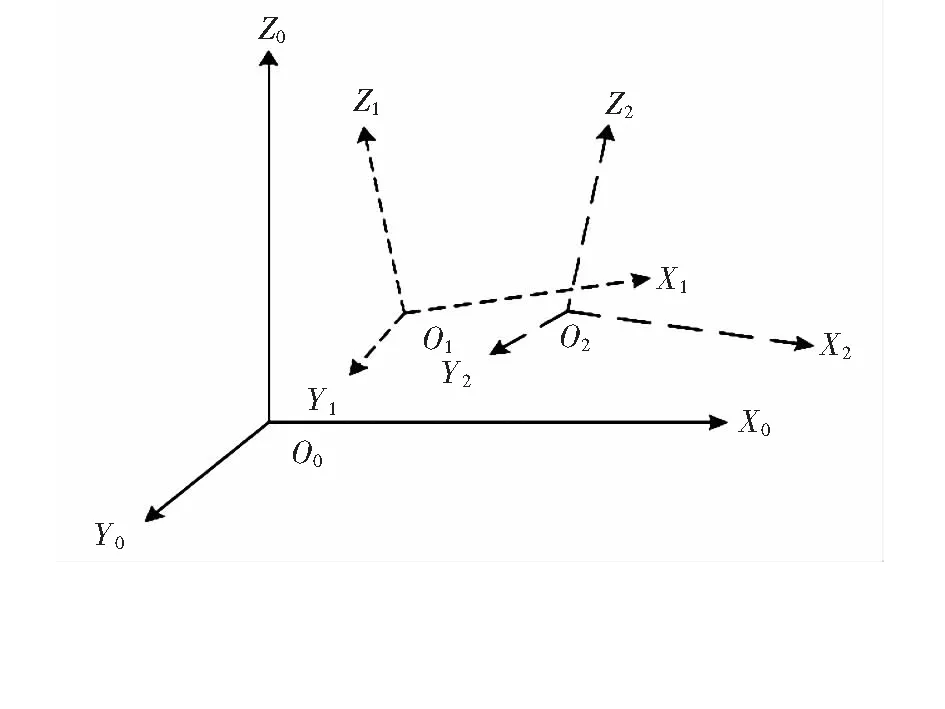
圖1 轉站示意圖

Q=RP+T。

(1)

通過SVD算法[9]、四元數法[10]、正交矩陣法[11]即可對角度參數R和距離參數T進行求解，即可得到當前站位下全站儀測量坐標系和基準坐標系的轉換關系。同時，在不同站位下，測點與公共點的相對空間位置保持不變，即可將當前站位下全站儀所測得的測點坐標轉換至基準坐標系下，多級轉站的過程即為轉站的迭代過程。

1.2 轉站誤差

設x為轉站測量過程中測點的真實空間坐標，x0為該測點經過轉站后的理論空間坐標，Δx為該測點在轉站測量過程中所產生的測量誤差，R0和T0分別為轉站過程中的理論角度參數和距離參數，ΔR和ΔT分別為轉站過程中的角度參數誤差和距離參數誤差，I為單位矩陣，則測量系統誤差δ可以表示為：

δ=R(x+Δx)+T-x0=R(x+Δx)+T-(R0x+T0)=(R-R0)x+ΔT+RΔx=(ΔR-I)R0x+ΔT+RΔx。

(2)

同時，可令R0x=X,則(ΔR-I)X+ΔT=CJ，

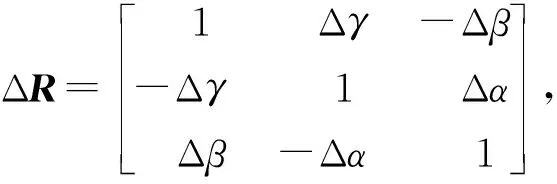
J=[Δα,Δβ,Δγ,ΔT1,ΔT2,ΔT3]。

Δα、Δβ、Δγ分別為繞X、Y、Z軸旋轉的角度誤差；ΔT1、ΔT2、ΔT3為ΔT在X、Y、Z軸的3個分量。

最終，測量系統誤差δ可以簡化為：

δ=CJ+RΔx,

(3)

式中，C為測量點的位置矩陣；J為轉站參數誤差矩陣；CJ表示測量系統的轉站誤差。

由公式(2)和公式(3)可知，測量系統的誤差主要由轉站誤差和測點測量誤差構成[12]，而轉站誤差的主要來源為公共點的測量誤差，因此，利用跟蹤靶球提高公共點和測點的測量精度來降低系統測量誤差具有理論可行性。

2 試驗與分析

為了對上述方法進行驗證，本文首先在單站條件下，對全站儀分別配合旋轉標靶和跟蹤靶球2種方法的測量精度進行了對比，之后通過多級轉站實驗，分析了在經過誤差傳遞后，旋轉標靶和跟蹤靶球2種不同精度公共點對測量系統誤差的影響。

2.1 試驗概述

2.1.1 試驗場地

圖2為試驗場地示意圖，本次試驗在艦船質量檢驗實驗工藝艙內的固定結構物上選取5個點位，在同一點位附近分別布置旋轉標靶和跟蹤靶球基座2種不同類型的公共點，另外，在測量平臺上分別布置跟蹤靶球和旋轉標靶2種不同類型測點各6個。利用全站儀分別在Ⅰ、Ⅱ、Ⅲ、Ⅳ4個站位設立測站坐標系，對公共點和測點進行觀測。

2.1.2 儀器設備

1)全站儀。本文采用拓普康MS05AX-Ⅱ型全站儀，如圖3所示，其配合旋轉標靶的測量精度可以達到0.5 mm，其搭載的電動驅動，可以實現自動跟蹤、自動照準等功能。

2)跟蹤靶球。本文采用跟蹤靶球中的角隅棱鏡反射器進行測量[13]，如圖4所示，其光學中心偏差小于0.006 mm，球形偏差小于0.001 5 mm。

圖2 試驗場地示意圖

圖3 拓普康MS05AX-Ⅱ型全站儀

圖4 角隅棱鏡反射器

角隅棱鏡反射器內部反射部分由1個三面相互垂直的角錐棱鏡構成，角錐棱鏡的3個垂直面上各涂有一層反射涂層，并且，角錐棱鏡的光學反射中心與球形外殼的幾何中心重合，保證了從任意角度射入角錐棱鏡的光線經反射后均可沿原方向返回，即利用全站儀進行測量時，當激光束從任意角度射入跟蹤靶球，所測點均為跟蹤靶球幾何中心。

參考文獻[8]已經對跟蹤靶球在不同角度入射光照射下的精度進行了驗證，結果顯示跟蹤靶球的測量精度受入射光角度影響較小。

2.2 單站測量精度試驗

2.2.1 試驗方法

1)在同一站位下，利用全站儀分別對旋轉標靶和跟蹤靶球2種不同類型的測點進行測量，每個測點測量10次。

2)在同一站位下，測點坐標的平均值即可認為是測點坐標的真實值，而測量值和平均值的差值即為測量誤差。據此，計算每次測量時旋轉標靶、跟蹤靶球2種不同類型測點坐標誤差ΔX1、ΔX2、ΔY1、ΔY2、ΔZ1、ΔZ2和位置誤差ΔMag1、ΔMag2，并分析其數據穩定性。

2.2.2 試驗結果及分析

由于全站儀配合旋轉標靶在標準測量模式下的角度傳感器和距離傳感器存在一定的機械誤差，并且，在實際測量過程中，人為操作誤差也無法避免，所以，測點的測量精度通常會小于理論精度。圖5所示的是在全站儀配合2種不同類型測點的誤差曲線，試驗結果表明，全站儀配合跟蹤靶球所得到的測點坐標，誤差更小，且數據穩定性更高，與兩者的理論精度相符。

2.3 轉站測量精度試驗

2.3.1 試驗方法

1)為減小測點的測量誤差對試驗結果的影響，選取跟蹤靶球作為測點。

2)利用全站儀分別對測點進行單級、兩級和三級轉站測量。如圖6所示，轉站測量時，先分別在各個站位利用全站儀對公共點進行測量，得到公共點坐標后，可求取相鄰兩站的坐標轉換參數，從而將測點坐標轉換至目標站位下，轉站順序為Ⅳ站→Ⅲ站→Ⅱ站→Ⅰ站。

測量過程中，為保證測量數據盡可能靠近真實值，每個測點測10次，公共點測3次，坐標數據取其平均值，轉站參數分別通過跟蹤靶球和旋轉標靶2種不同類型的公共點求取。由于在Ⅰ站所測得的測點數據不需要進行坐標轉換，同時，10次重復測量也可認為已經消除測量誤差，故可將在Ⅰ站所測得的測點數據作為測點坐標的真實值。

3)分別計算單級、兩級、三級轉站測量時，利用旋轉標靶和跟蹤靶球作公共點的坐標誤差ΔX1、ΔX2、ΔY1、ΔY2、ΔZ1、ΔZ2和位置誤差ΔMag1、ΔMag2，并分析其穩定性。

2.3.2 試驗結果及分析

根據測量誤差對測量系統精度影響過程的推導，在測點精度相同且公共點布置位置相近時，公共點的測量誤差是轉站誤差的主要來源，跟蹤靶球作公共點時的測量誤差小于旋轉標靶，故跟蹤靶球作公共點進行測量時的系統誤差也小于旋轉標靶。

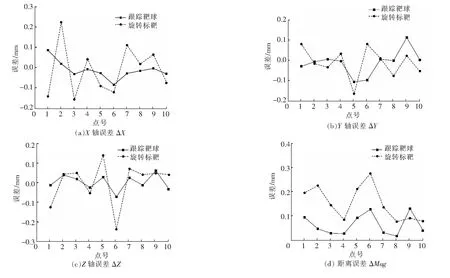
圖5 測量誤差分布圖

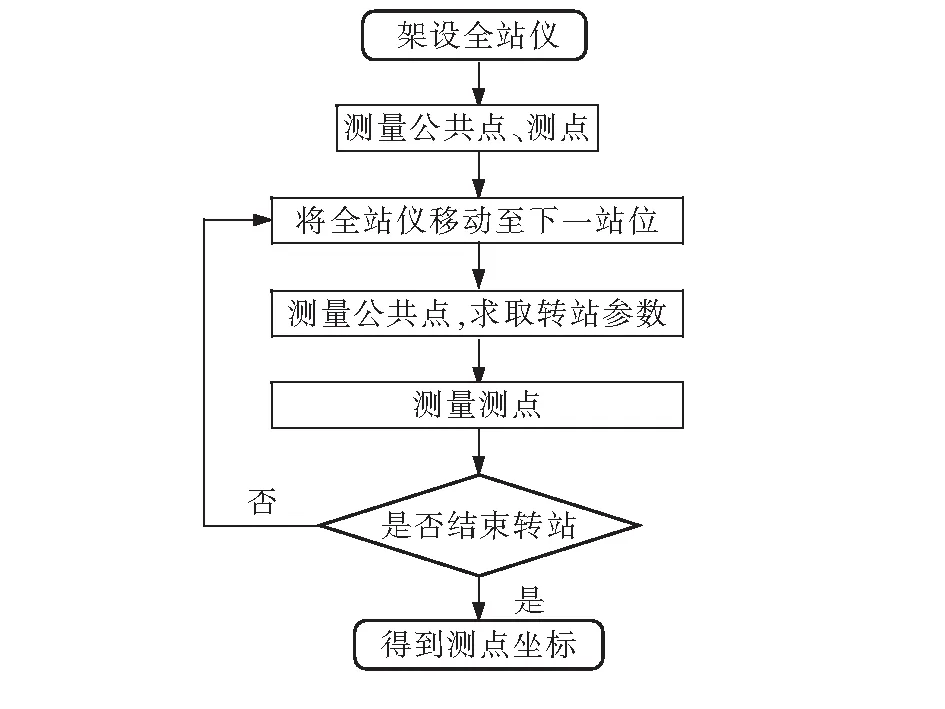
圖6 多站測量流程圖

表1是不同級數轉站測量時，分別用跟蹤靶球和旋轉標靶作為公共點的誤差和穩定性數據，試驗結果與理論推導符合。

3 結束語

本文對利用自動照準型全站儀配合跟蹤靶球測量的可行性進行了分析，并通過對比試驗，進一步證明了在轉站過程中，利用帶自動照準功能的全站儀配合跟蹤球可有效提高公共點和測點的測量精度，從而降低了測量系統的整體誤差，并且，測量效率也得到大幅提升，為目前船舶修造行業的測量提供了一種新的技術手段。

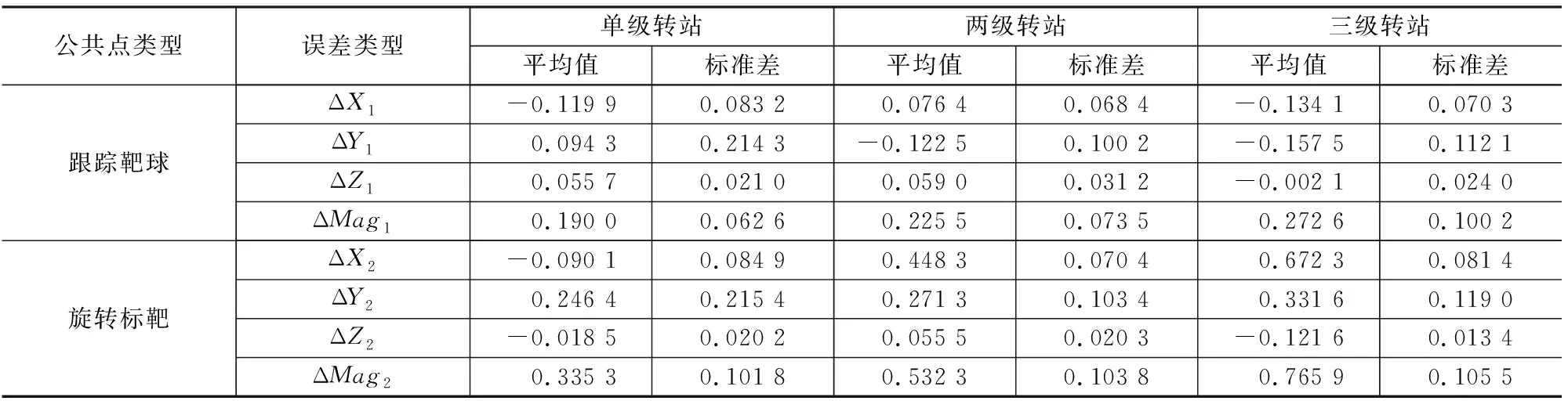
表1 多級轉站下的測量數據 mm